交叉梯度约束的三维极化率/电阻率联合反演

侯宇健，李桐林，张镕哲，陈汉波

吉林大学 地球探测科学与技术学院，长春 130026

0 引言

激发极化法是以岩、矿石的激电效应差异为物质基础，通过观测和研究大地激电效应，探查地下地质情况的一种电法分支方法。该方法在寻找金属矿、能源和工程地质等不同领域均有广泛的应用，尤其在寻找浸染状矿产资源方面效果显著[1]。

20世纪60、70年代，国内学者开始了解激发极化法并应用[2]。最初的反演方式多是用拟断面图进行定性解释或用一维方法来解释。阮百尧等[3]在二维电阻率/激发极化法反演程序的基础上进行了改进，使用算子线性化反演方法在国内首次实现了二维电阻率/极化率的反演。吴小平[4]提出了用共轭梯度方法的激发极化三维快速反演，实现了极化率的三维反演。

地球物理反演问题存在多解性[5]，为减少多解性的影响，一般期望电阻率与极化率的结构相同。Gallardo[6]最早提出了多参数联合反演方法，实现了两种物性在结构上互相约束的反演方式。李兆祥等[7]实现了基于交叉梯度约束的激发极化二维反演，首次进行了极化率电阻率的联合反演。闫政文等[8]实现了多参数的三维联合反演。

笔者在前人工作的基础上，基于等效电阻率公式，实现了三维电阻率/极化率正反演和联合反演。电阻率正演使用有限体积法进行数值模拟，反演过程中使用不精确牛顿法进行求解。使用共轭梯度法减少了需要占用存储空间，使三维反演速度和效率更高。推导了三维规则网格下的交叉梯度项及其梯度公式，提出了一种间接实现电阻率极化率联合反演的方式，并对各反演结果进行了分析。

1 正演理论

1.1 电阻率法正演

本文采用单元中心控制体积法[9]进行正演，对三维空间进行剖分，将地下空间离散为规则六面体单元，每一块的控制体积的基本方程为：

▽·(σ▽U)=-s

(1)

对其在控制体积Vijk内积分：

(2)

由高斯定理得：

(3)

等式右边为控制体积表面积分，等于各个面积分和：

(4)

经推导可得出控制方程：

λi+1, j, kUi+1, j, k+λi-1, j, kUi-1, j, k+λi, j+1, kUi, j+1, k+

λi, j-1, kUi,j-1, k+λi, j, k+1Ui, j, k+1+λi, j, k-1Ui, j, k-1-λi, j, kUi, j, k=Q

(5)

式中：

λi, j, k=-(λi+1, j, k+λi-1, j, k+λi, j+1, k+λi, j-1, k+λi, j, k+1+λi, j, k-1)

(6)

以此可以得到正演系数矩阵K，于是正演问题变成解决：

KU=q

(7)

线性方程组问题，q是源项向量。U为地下各点电位。

1.2 极化率正演方法

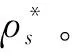
同样，用真实电阻率模型做一次正演，算出不带有激发极化效应的正演响应结果ρs。

利用等效电阻率公式，即可求出极化率的正演响应:

(8)

2 反演理论

2.1 电阻率联合反演方法

使用高斯-牛顿法建立目标函数，交叉梯度约束反演的目标函数为：

(9)

式中：

(10)

式中：D矩阵是数据误差矩阵；其中S是实测数据的误差；ε的存在是为保证分母不为0。β为正则化因子，是控制模型光滑程度的系数。W是模型光滑度矩阵，mref是期待的参考模型，d(m)为正演数据列向量，dobs为实测数据列向量。t为交叉梯度项，定义式为：

t(x,y,z)=▽mp(x,y,z)×▽mr(x,y,z)=(tx,ty,tz)

(11)

式中：mp，mr是两种物性的反演结果，如果反演初始模型是均匀的，那么t0是0。λ为交叉梯度项的权重。

对式(9)数据项泰勒展开，并对m求导，令其等于0，可得：

(JTDTDJ+βWTW+λBTB)·δm=-(JTDTD(d(mk-1)-dobs)+βWTW(m-mref)+λBT(t-t0))

(12)

式中：J是数据灵敏度矩阵；B是交叉梯度灵敏度矩阵；k是迭代次数。

令：

H=JTDTDJ+βWTW+λBTB

(13)

g=JTDTD(d(mk-1)-dobs)+βWTW(m-mref)+λBT(t-t0)

(14)

式(12)可写为：

H·δm=-g

(15)

要求解该式，如果用直接方法求解需要大量计算时间和储存空间，本文使用Dembo et al.[11]提出的不精确高斯牛顿法(IGN),解式(15)的具体算法为：

(a)在计算g时，计算出一个高精度的g(不用直接计算存储J，而是计算J和任意向量x的乘积Jx和JTx，详见下节)，保证下降方向正确。

(b)用预处理共轭梯度法(PCG)求解式(15)。

(c)在使用PCG求解时，以一个较低的精度计算J以得到H。

(d)在PCG中进行不超过五次的迭代，得到一个近似的模型改正量(每次迭代都要重新生成J)。

(e)得到的模型改正量δm可以对反演模型进行更新：

mi+1=mi+∝δm

(16)

式中：∝是线性搜索参数，用来控制模型修正量的大小。

以此可以求得极化率或其他参数约束电阻率反演的模型更新向量。

2.2 极化率联合反演方法

笔者在极化率单独反演中，利用等效电阻率公式将两次电阻率反演结果(等效电阻率反演结果和真电阻率反演结果)转换成极化率，由于此方法没有直接的极化率目标函数，前文描述中使用的联合反演理论无法直接算出极化率联合反演结果。笔者提出了一种间接实现极化率联合反演的方法。在不使用极化率直接反演的情况下成功实现了电阻率极化率的联合反演。具体过程为：

在已知极化率单独反演结果的基础上，进行由极化率约束的真电阻率反演，目标函数为：

(17)

用上一步得到的真电阻率反演结果ρ来约束等效电阻率的反演，目标函数为：

(18)

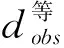
构造一个新的的目标函数：

(19)

通过等效电阻率公式：

(20)

求得的结果η即为电阻率约束的极化率联合反演结果。

2.3 目标函数梯度项的计算

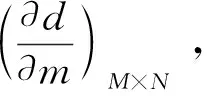
(21)

对上式两边对于电导率σ求导，得到：

(22)

由第二节可知，正演方程组可写为：

KU=q

(23)

两边同时对电导率求导可得：

(24)

把式(24)代入式(22)中，得到：

(25)

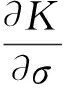
(26)

令：

(27)

则：

(28)

把式(28)右端看成正演方程组中的源项，按照正演的方法得到向量φ，代入式(26)，求得偏导数矩阵与任意向量x的乘积Jx。

偏导数矩阵的转制JT与任意向量y的乘积JTy的求解方法相似，在此不再赘述。

带有J的梯度项可以通过这种方式计算，以下为带有B和t的梯度项的计算方式。

交叉梯度函数t定义式为：

t(x,y,z)=▽mp(x,y,z)×▽mr(x,y,z)

=(tx,ty,tz)

(29)

彭淼[12]将式中tx，ty，tz进行了离散化，具体形式为：

(30)

(31)

(32)

式中：m的下角标p，r代表极化率和电阻率，上角标代表网格离散化过程中网格位置(图1)。

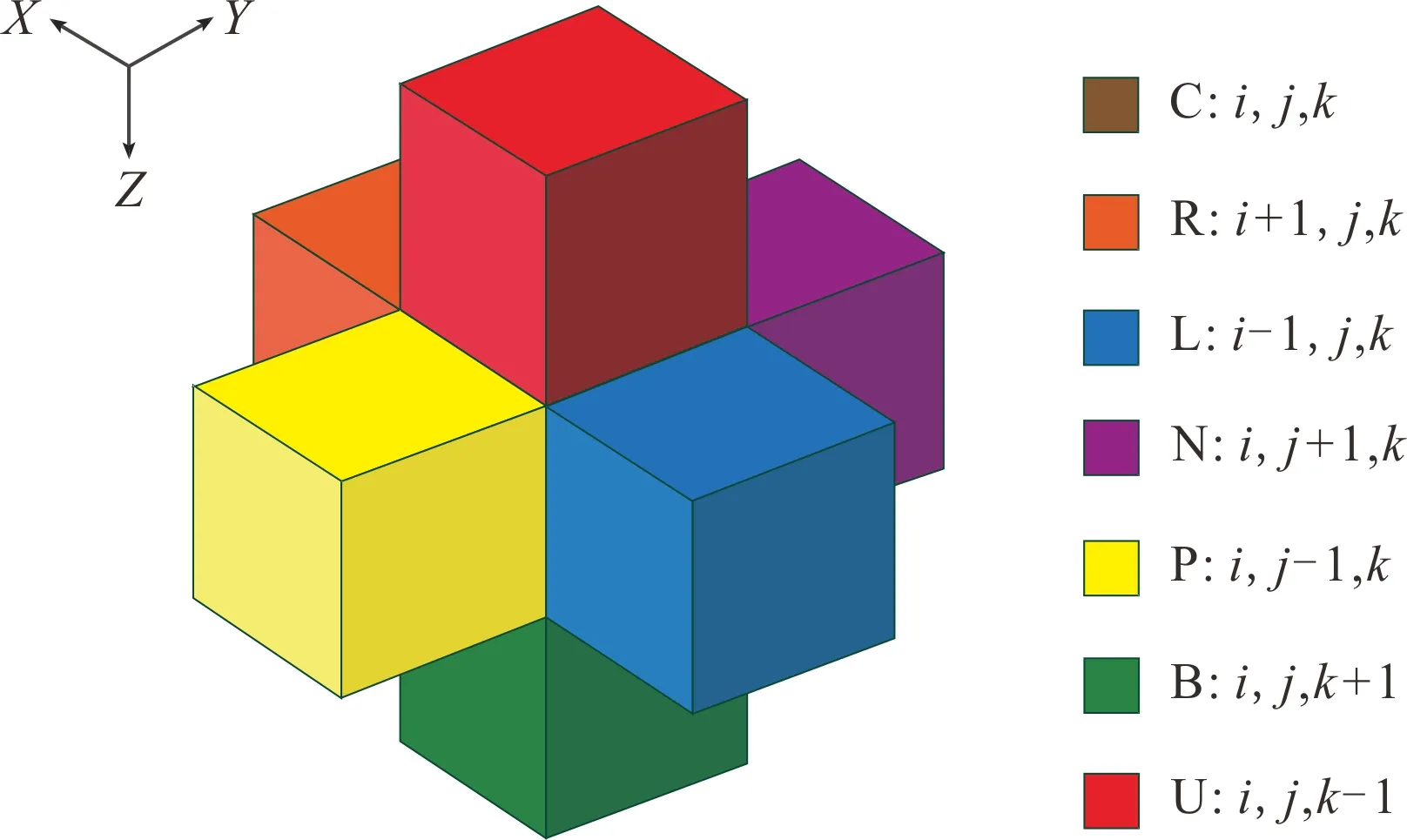
图1 交叉梯度项网格离散示意图Fig.1 Grid discrete diagram of cross gradient term

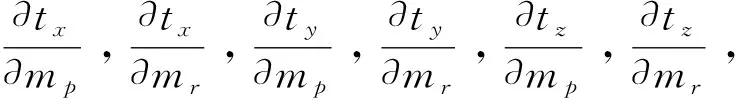
2.4 交叉梯度网格离散化边界的处理方法

笔者采用中心差分方式对交叉梯度项进行离散化。闫政文[8]推导了详细的三维交叉梯度函数公式，提出了在中心差分网格情况下的交叉梯度函数公式，将地下网格分为4类：内部网格、边界面网格、边界线网格和边界点网格。每一种网格的交叉梯度项公式都不同。所有梯度项一共是24个公式。笔者提出了一种将地下网格增加假想层的方法。只需要使用上文提到的3个公式及其导数即可表示出所有位置网格的交叉梯度项。具体方法是在反演网格外面假想地增加一层。如图2所示(透明网格为假想层)，前述反演网格变成了内部网格，可以用内部网格公式进行计算。右侧三个图分别为tx，ty，tz的示意图。假想层的物性参数与反演初值相同，保证交叉梯度项在边界附近的稳定性(均为0)，而又不影响感兴趣区的交叉梯度结果，提高了编程效率。

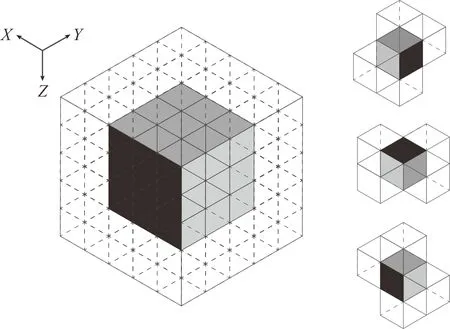
图2 交叉梯度项假想层示意图Fig.2 Imaginary layer diagram of cross gradient term

2.5 交叉梯度项计算可靠性验证

为了验证本程序提出的计算交叉梯度项及其导数的算法的可靠性，本文设计了如下理论模型：电阻率模型随深度渐变，极化率模型是一个6 m*4 m*4 m的高极化异常体埋藏在背景极化率为0的区域(图3，图4)，均为yz剖面。

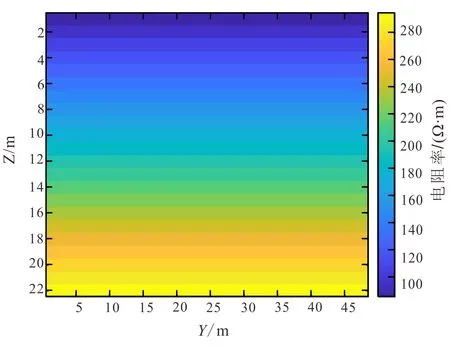
图3 电阻率理论模型(可靠性验证)Fig.3 Theoretical model of resistivity (test)

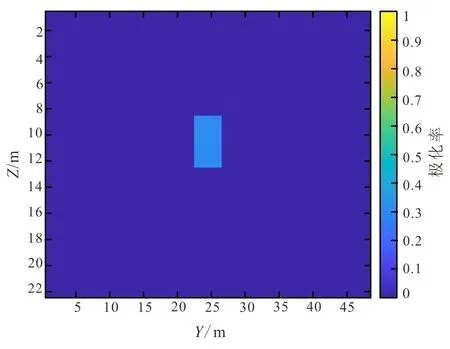
图4 极化率理论模型(可靠性验证)Fig.4 Theoretical model of polarizability(test)

用理论模型计算交叉梯度的tx，ty项，得到的结果(图5，图6)。

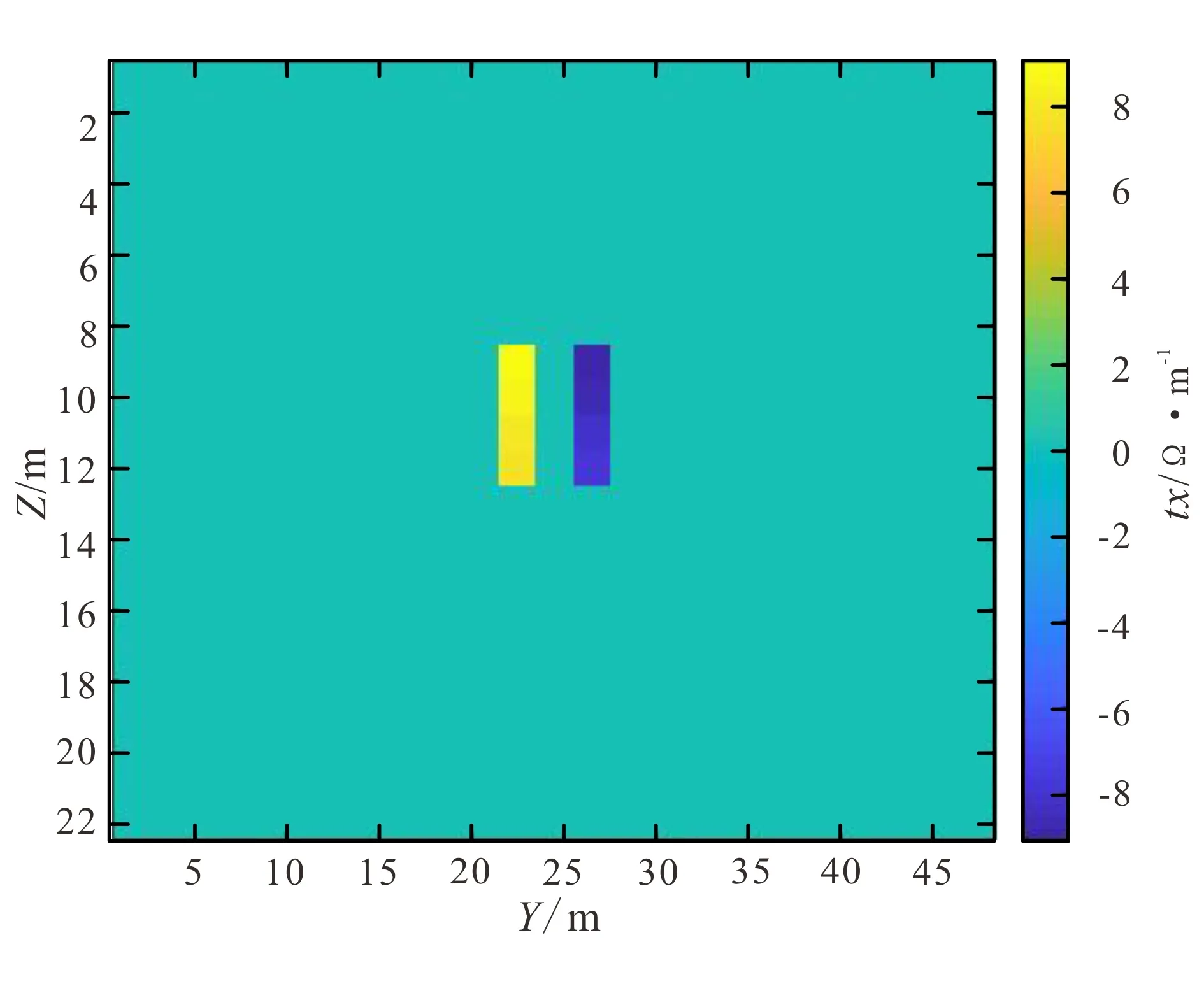
图5 交叉梯度项tx在YZ方向上的剖面图Fig.5 Cross gradient term tx in YZ direction

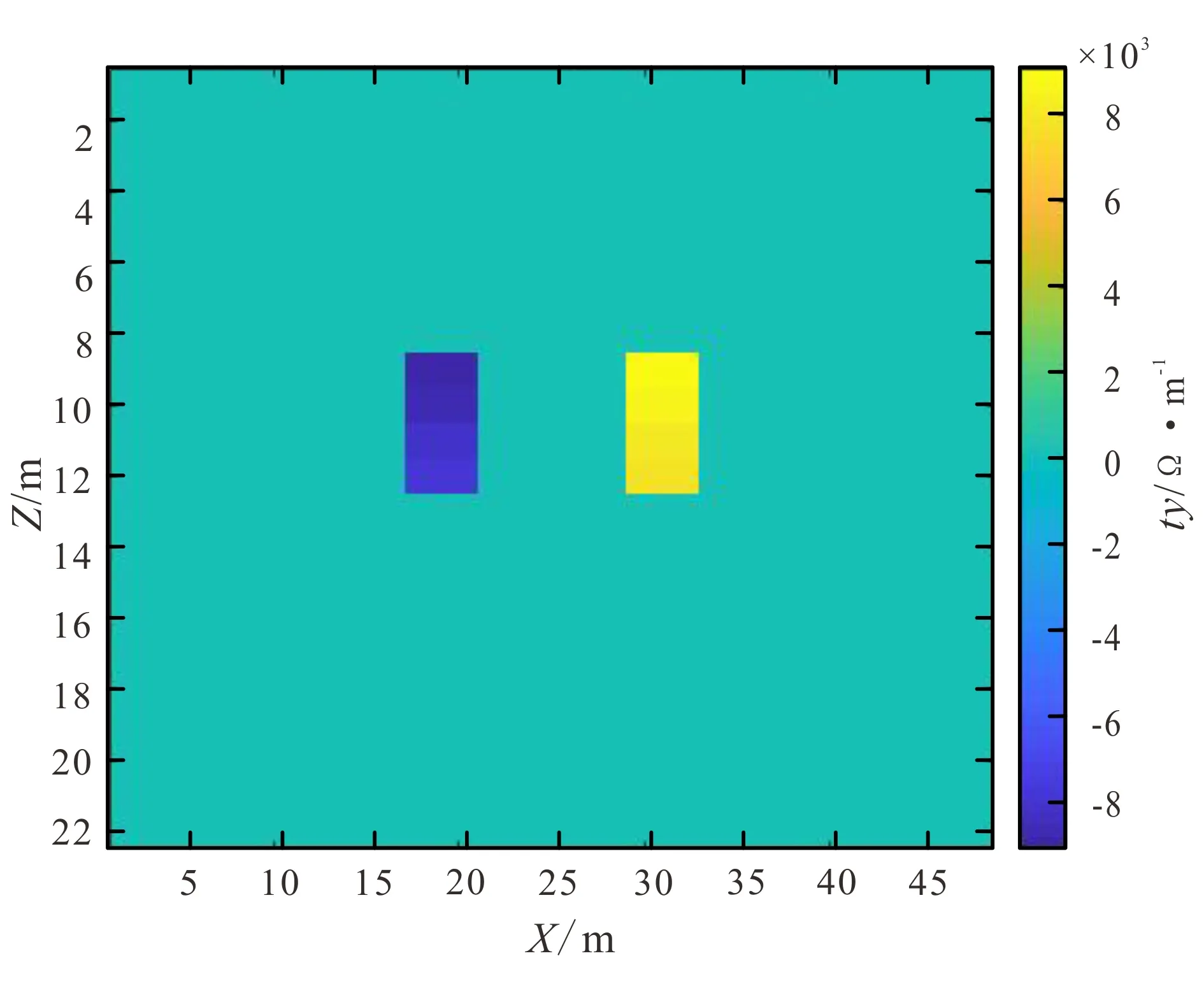
图6 交叉梯度项ty在XZ方向上的剖面图Fig.6 Cross gradient term ty in XZ direction

由于X方向和Y方向网格划分不同，导致XZ方向上的交叉梯度值看起来更宽。另外由于电阻率理论模型在XY方向上均匀，交叉梯度项tz的值为0。

观察上述交叉梯度结果可知，在物性变化的边界交叉梯度值不为0，在其他区域交叉梯度项均为0。由此可证明交叉梯度项t计算的可靠性。

3 模型试算

本文用理论模型进行试算，采用井下三极装置，网格剖分情况为48 m*24 m*22 m。异常体情况如图所示(图7，图8)，异常体A(左侧)和异常体B(右侧)大小形状相同。电阻率相同，右侧异常体B有极化率异常，异常体A没有极化率异常。

图7 电阻率正演理论模型Fig.7 Theoretical model of resistivity forward modeling

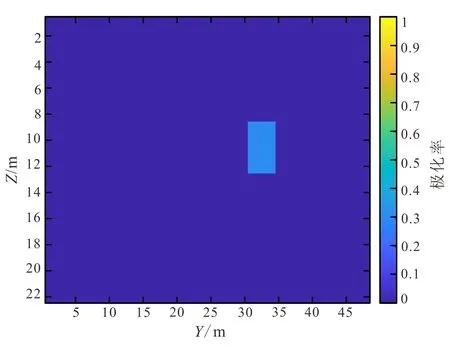
图8 极化率正演理论模型Fig.8 Forward model of polarizability

图9为电阻率单独反演结果，图10为极化率单独反演结果，图11为电阻率联合反演结果，图12为极化率联合反演结果。可以看出，无论是电阻率结果还是极化率结果，在两种异常同结构的情况下，电阻率/极化率联合反演相较于单独反演在数值恢复上效果更好，在两种异常结构不同的情况下，交叉梯度联合反演的效果和单独反演效果相同。这是因为交叉梯度值只在两种物性同时变化时才有异常，在任意一种物性均匀的情况下均为0，这时交叉梯度项对反演结果没有影响。

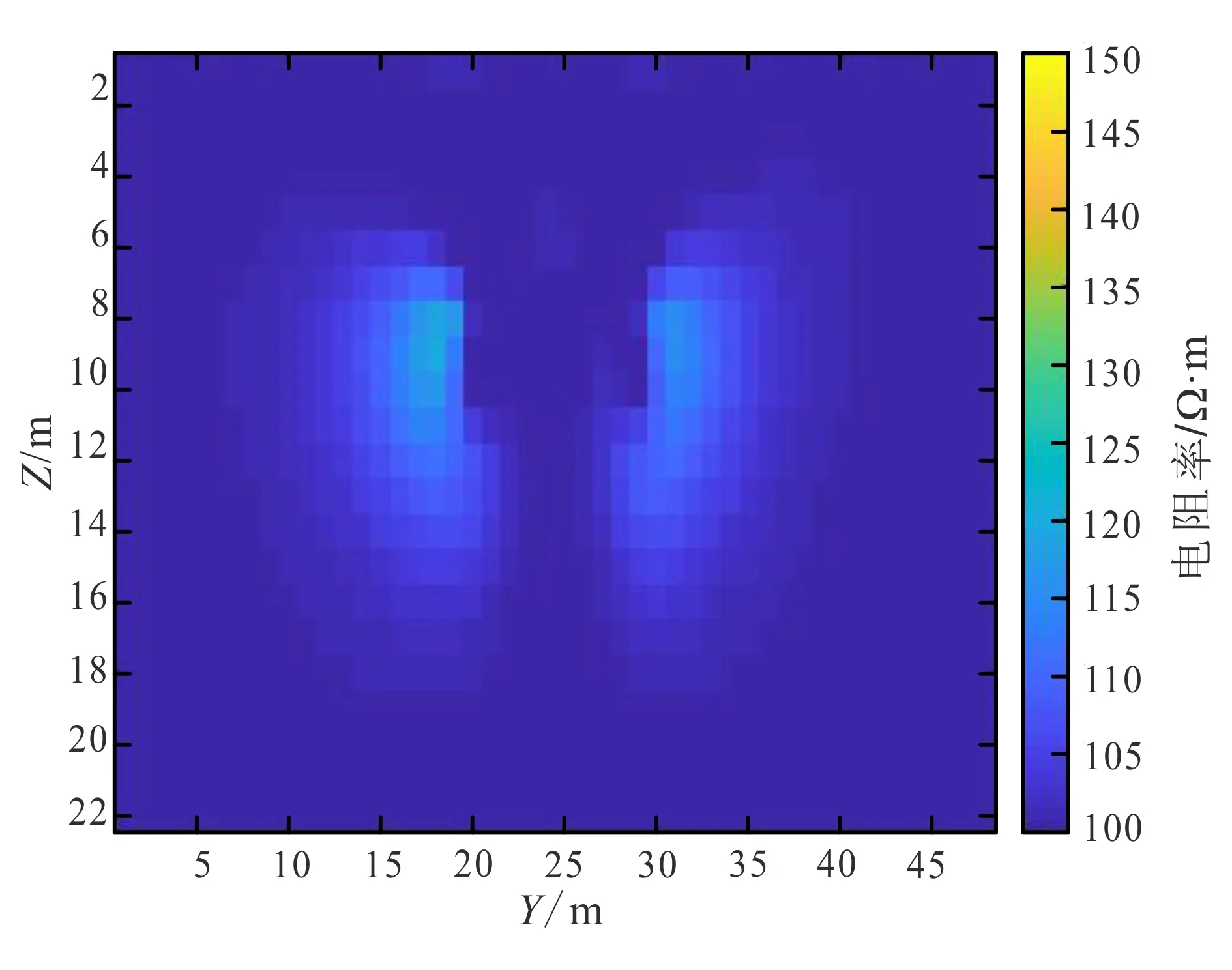
图9 电阻率单独反演结果Fig.9 Single inversion results of resistivity

图10 极化率单独反演结果Fig.10 Single inversion results of polarizability

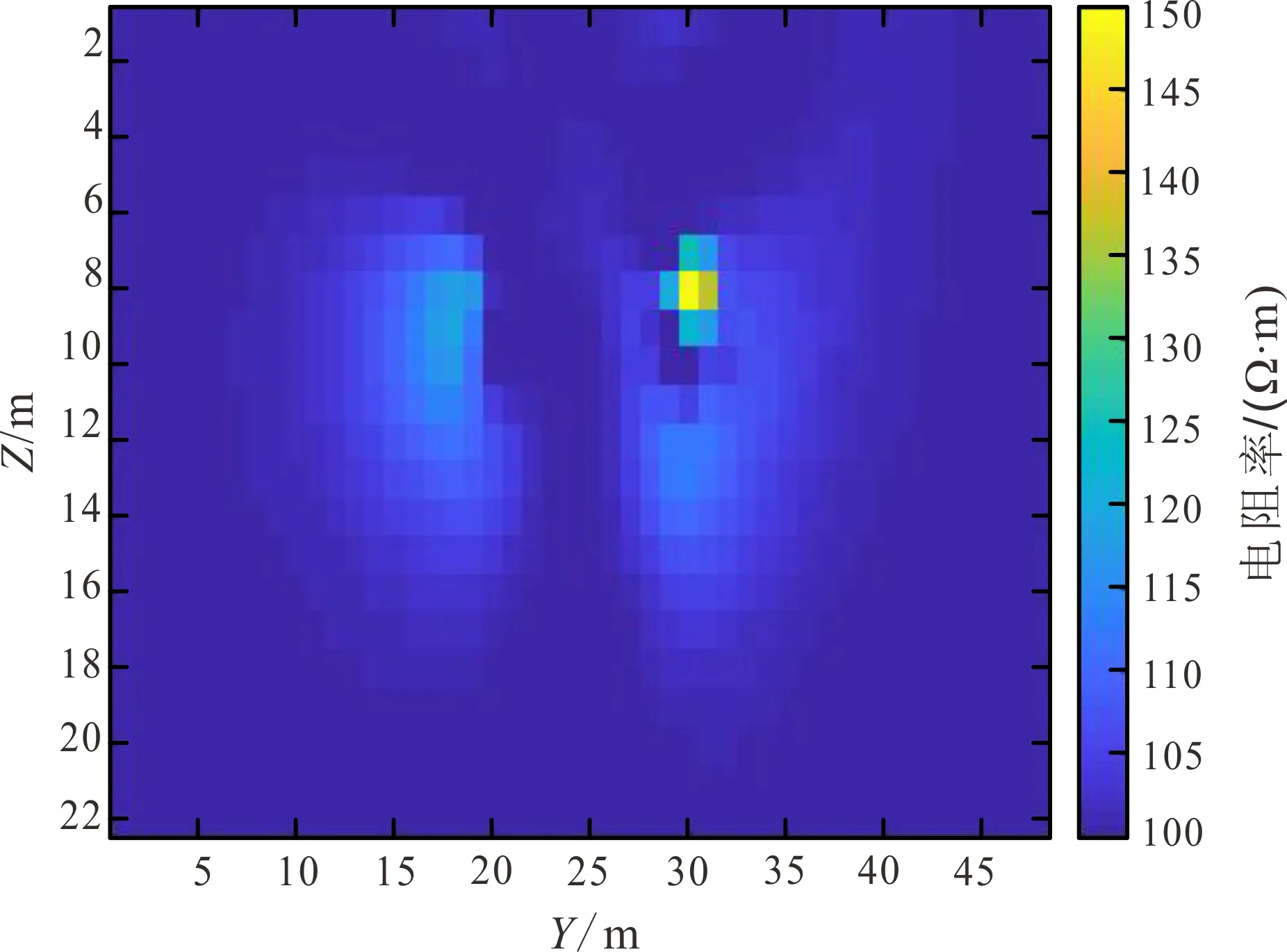
图11 电阻率联合反演结果Fig.11 Joint inversion results of resistivity

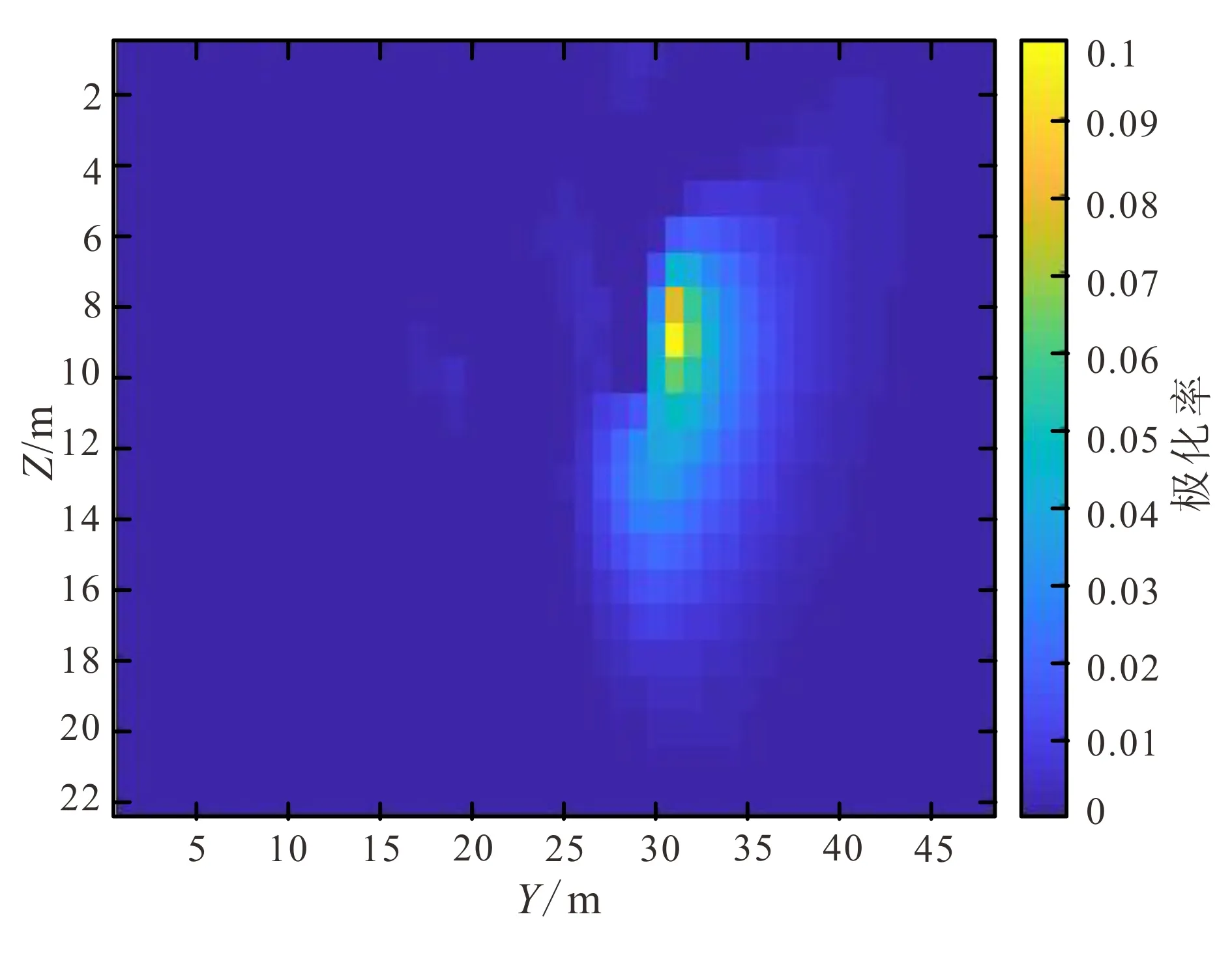
图12 极化率联合反演结果Fig.12 Joint inversion results of polarizability

4 结论

(1)交叉梯度约束反演比单独反演对同结构异常体的异常值恢复效果更好，符合预期成果。

(2)不同结构异常体的联合反演效果与单独反演相同，交叉梯度项只对同结构的异常体起作用。