主成分分析和字典学习联合地震数据去噪方法

朱鹤文,韩立国，陈瑞鼎

吉林大学 地球探测科学与技术学院，长春 130026

0 引言

在地震资料采集过程中，由于受到周围环境和地下因素的影响，不可避免地会采集到随机噪声。这会对有效信号产生严重干扰甚至导致有效信号变形，从而使地震数据的质量降低。为获得高信噪比的地震数据，使地震资料能更真实地反映地下的地质情况，如何突出有效波的同时抑制干扰波成为地震数据处理的主要研究内容之一。为解决这个问题，前人尝试了许多方法来压制地震数据中的随机噪声[1-2]，目前最常用的方法有傅里叶变换[3]、小波变换[4-6]和多项式拟合[7]等，虽然这些方法在一定程度上可以抑制随机噪声的影响，但各自均存在一些不足。例如，傅里叶变换是一种全时域变换，不能很好地区分地震数据的局部特征，小波变换对地震数据边缘的处理能力较弱等。

近年来，随着稀疏表示理论[8]的兴起，开始利用地震资料在某个变换域内的可稀疏性和可分离性去除随机噪声的影响[9-10],例如使用一系列的固定基字典方法消除噪声。由于这些方法的基是提前选定的，在数据处理过程中并不会随数据特征的变化而变化，导致其只对某些信号有较好的处理效果，不具备自适应性。后来提出了根据数据特点自适应的改变基函数的方法，如Olshausen et al.[11]在完备字典的基础上提出了自适应学习型超完备字典，该字典通过不断的学习训练更新字典获得更稀疏的信号表示。唐刚等[12]将学习型超完备字典用于地震数据去噪并取得了很好的效果。

超完备字典的精确性决定了地震数据稀疏表示效果的好坏，传统的K-SVD字典中使用奇异值分解来更新字典原子中的误差项，其重构的误差项与真实误差项之间存在一定残差，因此得到的字典不是最优的。本文将K-SVD字典与PCA算法相结合，利用PCA代替SVD对误差项进行特征提取，用提取到的最大特征向量来更新字典原子，PCA重构的误差项与真实误差项之间残差更小，训练后的字典对数据稀疏表示效果更好。笔者通过对复杂模型合成地震记录以及实际地震记录进行去噪实验，对比PCA、K-SVD以及本文算法对地震数据的去噪效果，验证了本文方法在地震数据去噪中更有优势。

1 方法原理

1.1 主成分分析算法

主成分分析法(principal component analysis,PCA)是一种基于统计理论的字典学习算法，被广泛应用于数据压缩[13]、人脸识别[14]和图像去噪[15-16]等领域。PCA算法主要思想是将方差的大小视为对信息衡量的标准，方差越大，代表其所提供的信息就越多，反之，则越少。PCA算法的实现是通过对数据的协方差矩阵进行特征值分解，分解后的特征向量对应数据的主成分，与特征向量相对应的特征值代表数据在各个主成分上的权重。PCA是一种线性变换，变换后各个主成分分量之间彼此线性无关。随着主成分编号的增加,该分量所包含的信息量就越小。笔者认为除主要成分外，其他主成分分量为噪声分量,这使得这种变换在损失数据较小的情况下去除了噪声。根据PCA的原理，结合地震数据实际情况，给出PCA算法的过程：

对于由n个检波点与时间上m个采样点得到的地震数据矩阵X(X∈Rm×n),PCA算法主要分为以下4步：

(1)将数据中心化处理：

(1)

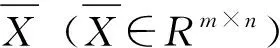
(2)计算协方差矩阵

(2)

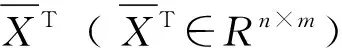
(3)将协方差矩阵特征值分解

C=UΛUT

(3)

式中:C为数据的协方差矩阵；Λ(Λ∈Rm×m)表示特征值矩阵，是一个对角矩阵，Λ中元素数值越大，代表其对应的特征向量所包含的信息越多。U(U∈Rm×m)表示特征值矩阵Λ对应的特征向量矩阵，UT(UT∈Rm×m)是U的转置，被称为旋转矩阵，用来将数据转换为主成分。

(4)去除含有噪声的低阶主成分，完成数据重构：

(4)

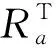
1.2 K-SVD字典学习

K-SVD[16]是K-means算法的一种泛化形式。其主要思想是利用奇异值分解方法对误差矩阵进行更新，从而得到更新后的字典原子以及相应的稀疏系数。K-SVD字典学习算法求解如下优化问题：

(5)

式中:Y表示给定训练数据；D表示字典矩阵；X表示稀疏系数矩阵；F表示F范数；xi是稀疏编码矩阵X中的行向量，代表字典矩阵的系数；T0表示稀疏系数中非零元素最大值。

式(1)是一个有约束问题，利用拉格朗日乘子将其转化为无约束问题：

(6)

K-SVD字典学习过程可分为3个步骤：

(1)准备阶段：给定的原始训练集为Y。给定初始化字典为D，初始化字典可以通过两种方式获得：①从样本中提取初始化字典；②给定一个字典作为初始化字典。

(2)稀疏编码阶段：根据给出的初始化字典，根据训练集Y与初始化字典矩阵D求解稀疏系数矩阵X。求解方法有很多，如匹配追踪算法[17]、正交匹配追踪算法[18-19]、快速迭代收缩阈值算法[20]等，本文采用正交匹配追踪算法。

(7)

(8)

(9)

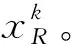
1.3 主成分分析和字典学习联合方法的去噪原理

在K-SVD算法中，通过对误差项进行奇异值分解来更新字典原子，这个过程属于对误差项的近似重构，与真实误差项存在一定误差。因此在K-SVD算法中，利用奇异值分解更新字典原子所构成的字典矩阵并不是最优的。本文结合K-SVD字典理论与PCA算法强大的特征提取能力，提出使用PCA算法代替SVD算法对误差项进行特征提取，用PCA算法提取的最大特征向量来更新字典原子。

这一过程表示为：

(10)

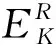
2 数值模拟实验

为验证基于主成分字典学习方法在地震数据去噪方面的优越性，本文对复杂模型进行数值模拟，分别用小波变换、PCA、K-SVD字典学习以及本文方法进行去噪处理比较。定义信噪比参数SNR(Signal Noise Ratio)来衡量去噪效果的好坏。

(11)

式中:s代表去除随机噪声后的地震数据；s0代表原始未加随机噪声的地震数据。

对合成记录加入的高斯噪声的概率密度服从高斯分布：

(12)

式中:均值μ=0；标准差σ=1；n为随机噪声的量级，即产生n个满足标准正态分布的随机噪声。

为验证本文方法的去噪性能，对复杂模型进行合成地震记录(图1a)，共有100道，道间距10 m，每道700个采样点，采样时间间隔0.001 s。对模拟地震记录加入0.6量级的随机噪声(图1b)，加入后信噪比为7.79 dB，对比图1a和图1b中红色箭头和黄色箭头所指部分，可以看出随机噪声对有效信号的干扰很严重，造成有效信号能量较弱的部分模糊形变。

a.合成地震记录；b.加噪声记录。图1 复杂模型合成地震记录和加噪声地震记录Fig.1 Complex model synthetic seismogram and seismic records with added noise

经过笔者多次实验，使用PCA对地震数据进行去噪时，选取前65～70个主成分(占比约0.945)，能取得最高信噪比。这里选取前67个主成分。对比图2中4种方法的去噪效果可以看出，这4种算法均能对地震记录中的随机噪声进行压制，但小波变换(图2a)对同相轴的表示能力不足，会使同相轴产生形变。PCA算法(图2b)红色箭头处的同相轴依然模糊，表明其对能量薄弱部分的有效信号去噪效果明显不如小波变换、K-SVD字典学习和本文方法，这是由于PCA算法会将弱能量的有效信号视为噪声并将其去除，使能量弱的同相轴变得模糊。K-SVD算法(图2c)和本文方法(图2d)去噪效果明显好于前两种算法，对噪声的压制比较明显，但对比之下可以发现，本文方法较K-SVD算法对随机噪声剔除的更干净，从黄色箭头部分也可以看出，本文方法对弱能量有效信号保护好于K-SVD算法。同时根据表1看出，本文算法去噪后信噪比较其他三者都有提升，其中较K-SVD算法提升约1.2 dB，表明本文方法在保护有效信号和压制噪声两方面都好于K-SVD算法及其他两种方法。

表1 复杂模型合成地震记录去噪信噪比Table 1 Denoise SNR of complex model synthetic seismogram

a.小波去噪；b.PCA去噪；c.K-SVD去噪；d.本文方法。图2 复杂模型合成地震记录去噪效果Fig.2 Denoising effect of complex model synthetic seismogram

为验证本文算法在不同噪声强度下的去噪效果，对合成地震记录加入不同量级的随机噪声，分别使用以上4种方法进行去噪处理并绘制去噪后的信噪比曲线(图3)，可以看出随着噪声量级的增加，4种方法去噪后的信噪比都在减小，但通过对比可以发现，本文方法去噪后的信噪比明显高于其他3种方法,相较于传统的K-SVD算法高出1～1.5dB，说明在不同噪声量级下，本文方法对K-SVD算法去噪效果有提升，这种提升在低量级随机噪声中表现尤为明显。

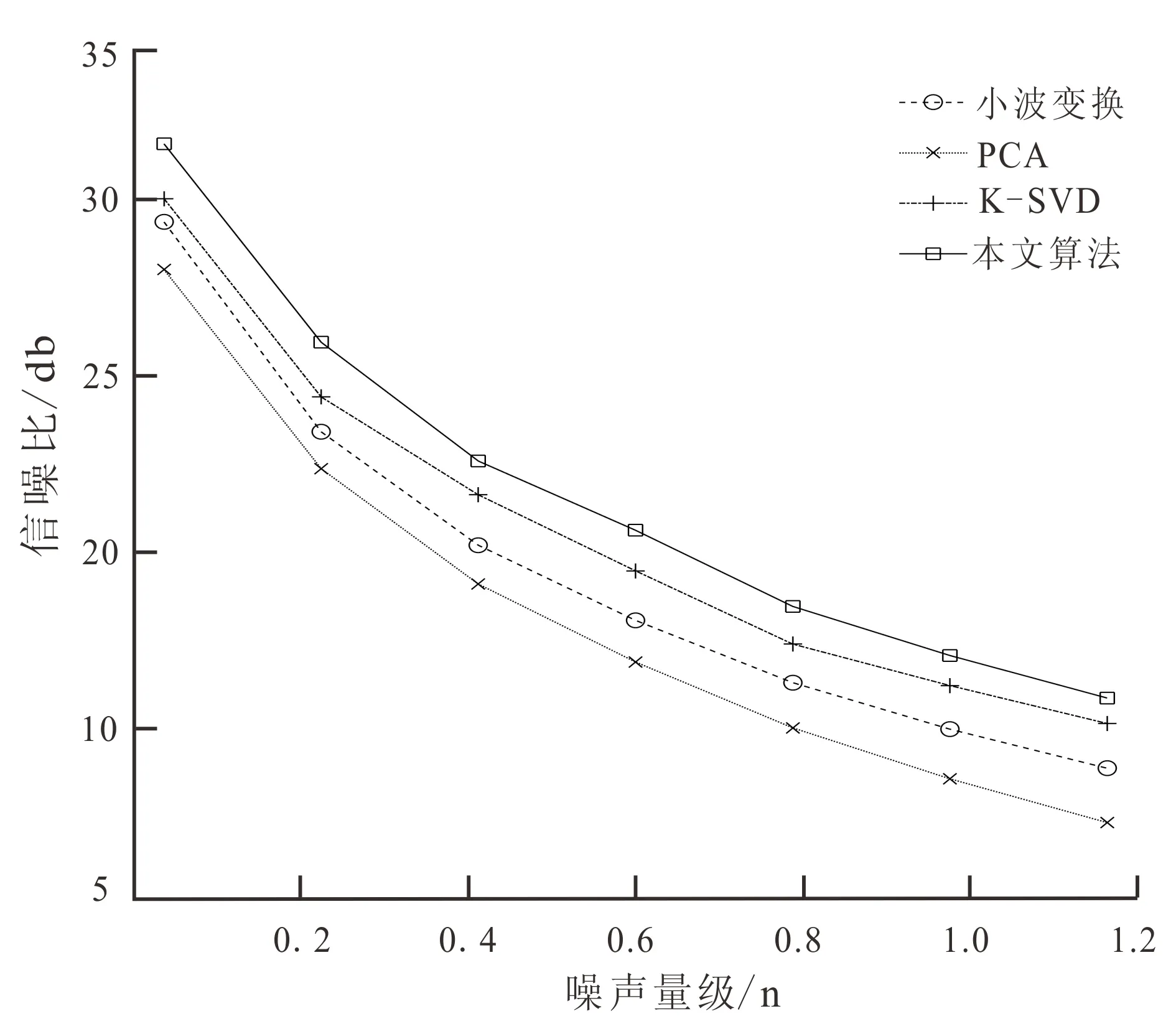
图3 复杂模型合成地震记录在不同随机噪声量级下的信噪比曲线Fig.3 SNR curves of complex model synthetic seismograms under different random noise magnitude

3 实际地震数据及分析

为检测本文方法在实际地震数据中的去噪能力，分别用小波变换、PCA、K-SVD以及本文方法对实际含噪声地震数据进行去噪实验对比。采用实际地震数据如图4所示，地震记录共61道，每道3 000个采样点，时间采样间隔为0.001 s。由红色箭头可以看出随机噪声对反射波同相轴产生严重畸变，导致反射波同相轴模糊，黑色箭头处可以看到背景噪声比较明显。

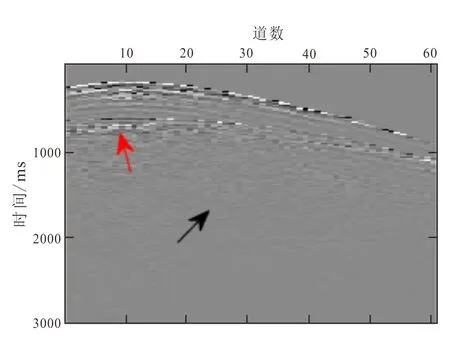
图4 实际地震记录Fig.4 Actual seismogram

图5为实际地震数据去噪效果图，可以看出对于实际地震数据去噪处理中，4种方法都取得了不错的效果。但小波变换(图5a)对于红色箭头处反射波同相轴部分的去噪效果不理想，PCA算法(图5b)同小波变换一样，对黑色箭头处的背景噪声压制有一定效果，红色箭头处有效信号部分去噪效果不明显，同时PCA算法在去除随机噪声的同时引入了条带状噪声。相比之下K-SVD算法(图5c)与本文方法(图5d)对于背景噪声的压制明显好于小波变换和PCA算法，但K-SVD算法在去噪过程中，对有效信号的损失比较严重，导致同相轴模糊，而本文算法无论是在去噪效果还是在对有效信号的保护上都要好其他3种算法。

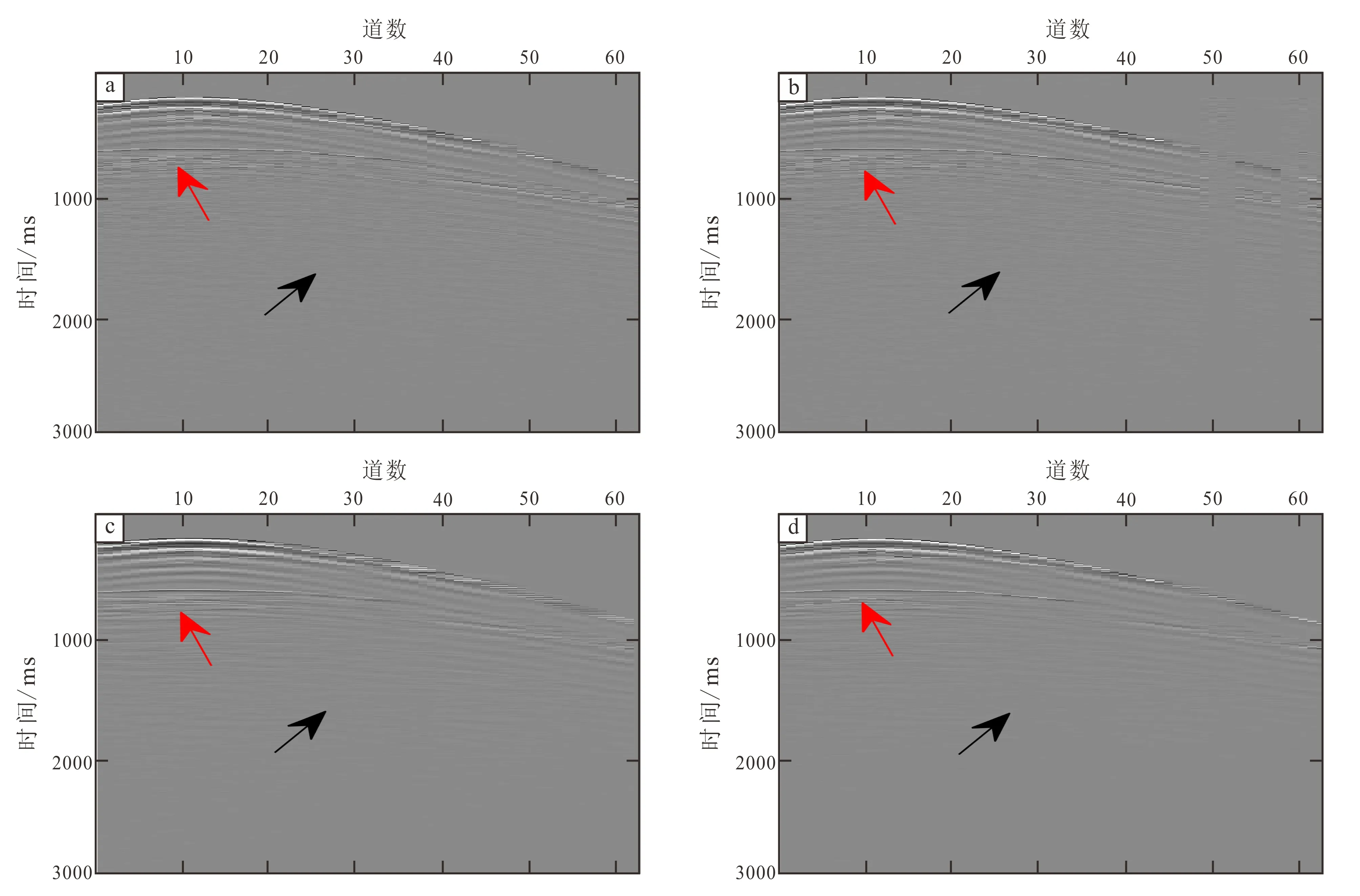
a.小波去噪；b.PCA去噪；c.K-SVD去噪；d.本文方法。图5 实际地震数据去噪效果Fig.5 Denoising effect of actual seismogram

4 结论

(1)对复杂模型合成地震记录的实验可知，在不同强度的随机噪声下，本文算法都能获得比其他3种算法更高的信噪比，在噪声能量较弱时表现尤为明显。

(2)对实际地震记录的实验可知，相较于K-SVD及其他2种算法，本文算法对有效信号的损害较少，噪声去除的更干净，同相轴更清晰。