激发极化中的赛格尔近似及饱和效应

庄严,李桐林

吉林大学 地球探测科学与技术学院，长春 130026

0 引言

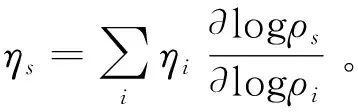
式中:ρs为视电阻率；ρi为地下第i块的真电阻率；ηs为视极化率；ηi为地下第i块的真极化率。

视极化率与极化率之间是线性关系，只要计算出了视电阻率对电阻率模型的偏导数矩阵，就可以计算视极化率，或者用已知的视极化率反演极化率。目前，根据赛格尔体激发极化理论[2]，利用赛格尔公式的线性反演方法得到广泛应用。在反演中，利用电位函数与模型参数间的关系计算偏导数矩阵，大大减少了计算工作量。根据Tripp et al.[3]提出的理论，阮百尧[4]利用互换定理给出了一种视电阻率对模型电阻率的偏导数矩阵简便计算方法。 Li et al.[5]的二维极化率数据反演、阮百尧等[6-7]的二维激发极化反演及黄俊革[8]的极化率反演都是利用赛格尔公式的线性反演。Li et al.在二维极化率数据反演中用了3种反演方法，第一种就是利用赛格尔公式的线性反演，后两者是非线性反演，对于利用赛格尔公式的线性反演他们作了这样的评述：赛格尔公式是一个线性公式，利用该公式反演的优势是只需解决一个线性反演问题，这种方法简单、快速，可以节约出大量的时间用于数据误差估计和选择更多的反演精度以达到更好的反演效果，且该方法对数据的测量误差不敏感，但其没有考虑非线性的影响，特别是极化率较大的情况[5]。刘海飞论述利用赛格尔公式的线性反演可以通过增加电阻率反演的迭代次数来改善电阻率反演结果从而改善极化率的反演结果[9]。柳建新等对线性反演和非线性反演进行了模拟、对比及分析，得出的结论与上述基本相同[10]。黄俊革在三维激发极化正演中利用赛格尔公式计算了视极化率[11]。

赛格尔在利用赛格尔公式对均匀半空间中的一个低阻球体模型进行了一维正演计算，发现当围岩电阻率不变时，随着球体电阻率不断降低，视极化率异常并非单调增大，而是先增大后减小，这种现象称之为饱和效应。利用赛格尔公式对该模型进行推导，得出在球体与围岩电阻率比值为0.5时取得视极化率最大值。据此认为激发极化法不适合寻找电阻率差异悬殊的极化矿体，这种电阻率有数量级上的差异会抑制IP效应。王庆乙则对饱和效应提出了异议，认为饱和效应完全是赛格尔近似公式计算造成的，在寻找良导致密铜矿和低阻炭质板岩矿的实践中并未出现饱和效应问题，且完成了铜球和石墨球的水槽实验，以进一步说明激发极化不存在饱和效应，同样适合寻找电性差异较大的极化矿体[12]。

针对赛格尔公式的近似精度问题以及饱和效应的认识问题，笔者进行了激发极化中赛格尔公式的推导，分别用等效电阻率法和赛格尔公式法两种方法进行了正演模拟和分析，通过对比这两种方法的正演结果，给出赛格尔公式的适用范围；同时对激发极化中的饱和效应进行正演模拟，研究了饱和效应的影响因素并分析了其物理实质。该研究对选择正确的激发极化正演方法及激发极化中饱和效应的认识有重要意义。

1 激发极化中的赛格尔近似正演理论

根据等效电阻率法正演理论：

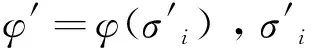
(1)

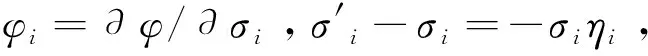
(2)

由视极化率定义

(3)

整理可得：

(4)

由于大多数极化体的极化率η远<1，因此

(5)

得出赛格尔公式：

(6)

以上为赛格尔公式推导过程，其中有两处进行了近似处理：一是在式(1)中将总场电位表达式用一次电位与各个极化体产生的二次电位线性相加；二是在式(6)中，等效视电阻率近似等于视电阻率。

实际地下的这种结构为非线性，

(7)

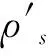
2 模型试算

2.1 赛格尔公式的验证

为了验证赛格尔公式计算的准确性，要求理论正演必须有解析表达式，确保理论正演正确，那么对有理论解析式的均匀半空间中单个极化球体以及有极化层的层状介质模型进行理论正演(等效电阻率法正演)计算，其结果与相应的赛格尔公式正演计算结果进行了对比。

均匀半空间中的极化球体视极化率曲线对比结果见图1。图1(a)对应的物理参数为：球体中心坐标(26,80)，半径50 m，极化率0.5，围岩不极化，球体与围岩电阻率比值 1.0。图1(b)对应的物理参数为：球体中心坐标(26,80)，半径50 m，极化率0.5，围岩不极化，球体与围岩电阻率比值 0.01。

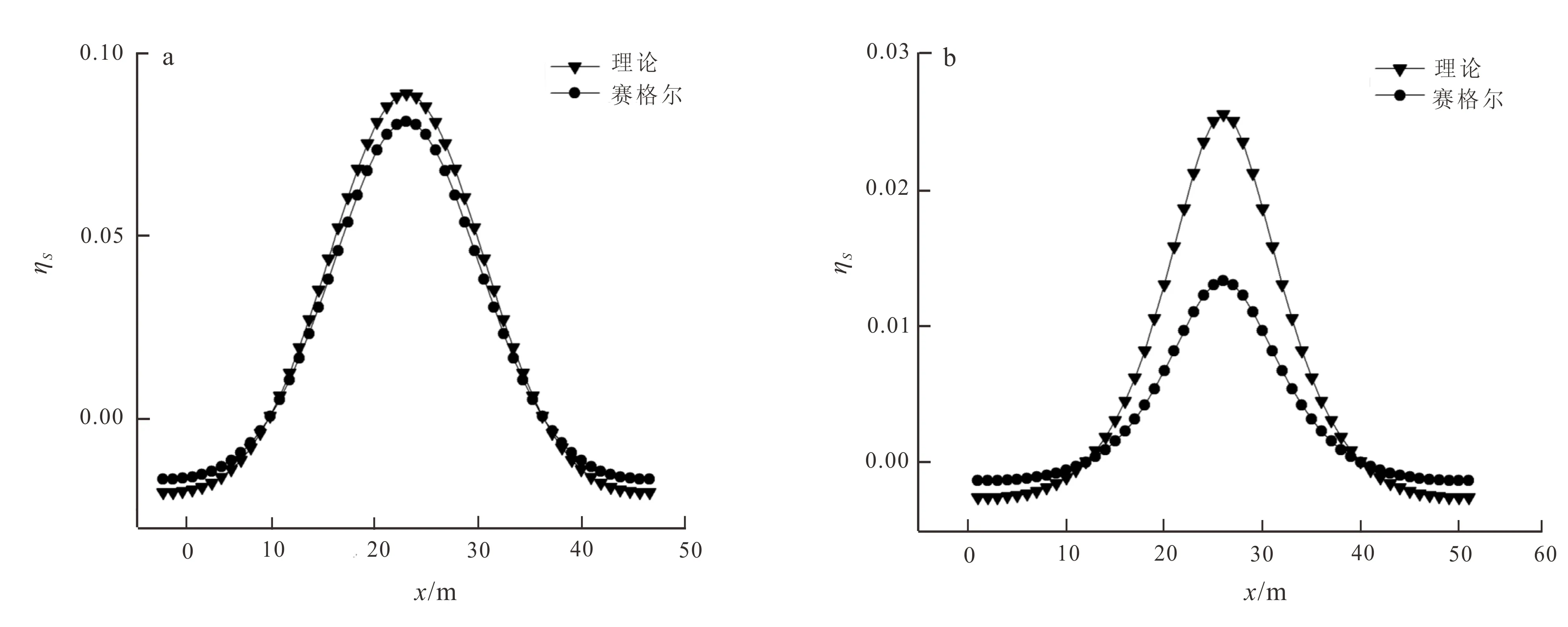
a.球体与围岩电阻率1∶1视极化率曲线对比结果图; b.球体与围岩电阻率1∶100视极化率曲线对比结果图。图1 均匀半空间中极化球体的视极化率曲线Fig.1 Apparent polarization curves of a polarization sphere in homogeneous half space

从图1可以看出在计算低阻高极化球体的视极化率上，赛格尔公式计算的视极化率异常要小于理论计算的异常，并且随球体电阻的降低其误差随之增大。

高极化率层状介质视极化率曲线对比结果见图2。模型为4层介质，第一二三层厚度分别为100 m、500 m、1 000 m，一二三四层的电阻率分别为10 Ω·m、100 Ω·m、1 000 Ω·m、10 000 Ω·m，极化率分别为0、0.2、0.5、0.8。

从图2可以看出，对于高极化的层状介质，利用赛格尔公式计算的结果出现较大误差。

对于极化率不是很高的层状地电结构进行正演计算(图3)。模型的厚度和电阻率同图2模型，但极化率变小。极化率分别为0、0.05、0.1、0，在不同极距下视极化率的计算结果如图3所示。

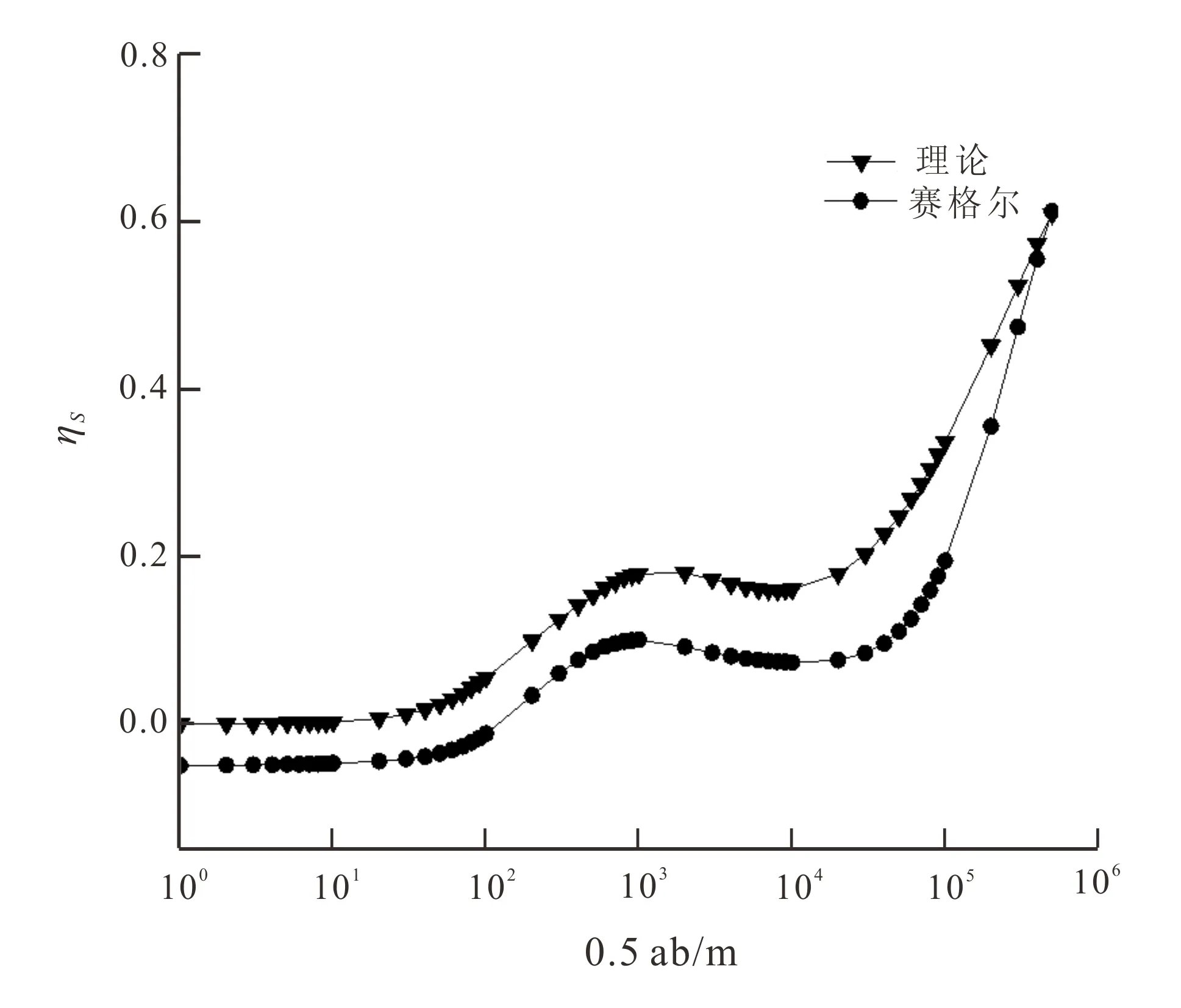
图2 极化率差别较大情况下层状介质的视极化率曲线对比Fig.2 Apparent polarization curves of a layered earth model in high-contrast polarization

从图3可以看到，对于极化率不是很高的层状介质，赛格尔公式计算结果同样出现较大误差，说明该公式对复杂的层状介质计算不准确。

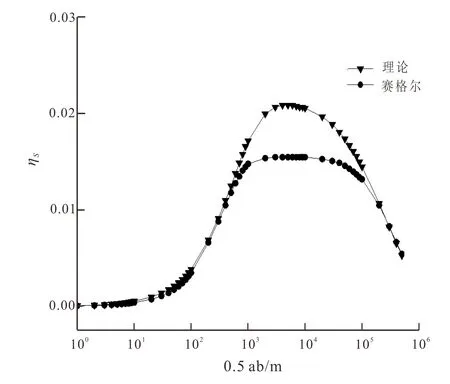
图3 极化率差别较小情况下层状介质的视极化率曲线对比Fig.3 Apparent polarization curves of a layer model in general-contrast polarization

综上，对多层有极化的层状介质或低阻高极化球体来说，赛格尔公式计算结果会有较大误差。这种情况表明，利用赛格尔公式反演极化率同样会出现较大的误差，即使可以通过增加电阻率反演迭代次数来改善电阻率反演结果进而改善极化率的结果，但这种改善只能是对反演曲线拟合程度的改善，无法避免赛格尔公式的近似性所造成的误差。

2.2 饱和效应的模拟

采用2.5维直流电法有限元正演进行二维视极化率正演模拟研究。给定的模型如图4所示，其正演结果见图5。

图4 正演模型及参数Fig.4 Forward calculation model and parameters

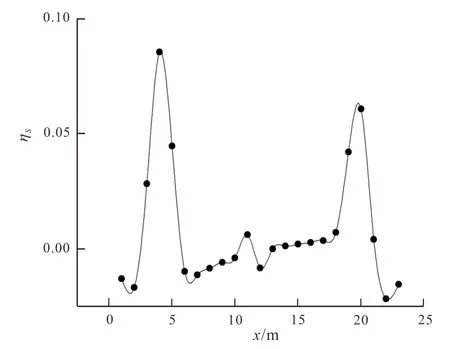
图5 二维正演模拟视极化率异常剖面曲线图Fig.5 Two dimensional forward modeling apparent charge ability anomaly map

图5说明在相对高阻体A上的视极化率异常要高于相对低阻B上的视极化率异常，这说明数值模拟中也能看到所谓的“饱和效应”的存在。

为了进一步说明饱和效应的规律，图6给出了一组不同球体半径r对应的视极化率异常值随μ12变化的曲线图，球体中心相同。

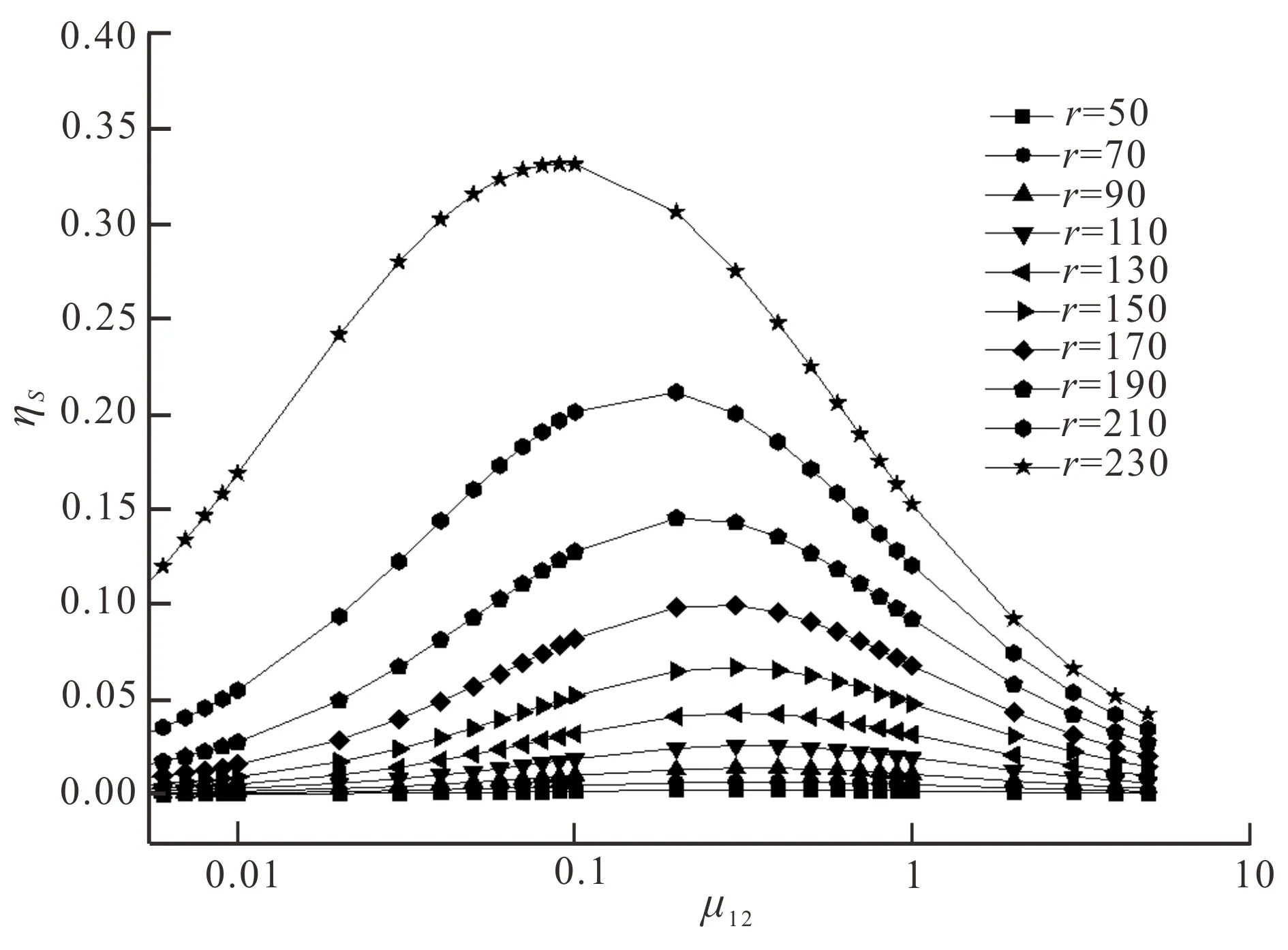
图6 球体视极化率ηs随μ12变化的对比曲线图Fig.6 Apparent charge ability ηs curves with different radius μ12

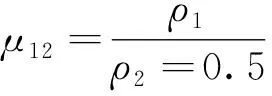
3 结论

(1)赛格尔公式在任何情况下，都是一个近似公式。特别是高极化情况下，利用赛格尔公式计算视极化率存在较大偏差。

(2)饱和效应不仅受电阻率的影响，而且受极化体大小影响，极化体越大，饱和极值所对应的μ12值越小，也就是说相对更低阻的极化才能达到饱和。

(3)用激发极化法研究特别低阻的极化矿床时，异常的极大值可能会偏离富集矿体中心，因此根据异常定性分析预测矿体的位置可能出现偏差。