基于奇异信号的钢桁-砼组合梁损伤识别

冯 麟， 周志祥，1b， 张 鑫， 唐 亮， 雷杨崑， 周孝桂

（1． 重庆交通大学a．土木工程学院；b．省部共建山区桥梁及隧道工程国家重点实验室，重庆400074；2． 中冶赛迪工程技术股份有限公司，重庆400013）

0 引 言

预制桥道板形式的钢桁-砼组合梁由于其在桥梁建设中的工业化、信息化、绿色化以及智能化等特点已逐渐成为组合结构桥梁的发展趋势［1］。此结构结合钢材抗拉与混凝土抗压两种材料力学性能，通过连接钢梁与混凝土板成为整体共同承受荷载、协调变形，从而具有施工速度快、生产效率高与收缩徐变小等优势［2-3］。然而，组合梁在长期服役过程中由于材料自身限制及诸多因素的影响会不断产生累计损伤，从而出现功能退化，进而影响其正常运营过程甚至垮塌灾难，因此尽早识别出早期损伤状况并给出合理维修建议，可确保其安全健康地运营，以达到排除安全隐患的目的［4］。

针对桥梁损伤识方法研究主要可分为基于动态响应与静态参量的识别［5］。在静态参量的影响线识别中，寇晓娜［6］首次利用挠度影响线对一个有机玻璃模型桥的损伤进行了初步识别探索；刘纲等［7］将桥梁损伤前后所产生的位移差视为损伤影响线，依据影响线拐点及峰值进行损伤位置与程度的判断；张珂苑等［8］提出了以箱梁跨中位移影响线的3 次差值作为损伤识别指标，但未进行试验验证；蔡建伟等［9］基于挠度影响线的一阶与二阶导数，针对一座简支T 梁进行损伤识别研究，但未涉及超静定结构的识别判断；陈志为等［10］综合应变与挠度影响线两指标实现损伤初步识别，在对多影响线进行信息融合后，以影响线计算概率分布函数增强损伤定位，缺点为需多种类型传感器进行信息融合。近年来，发展了许多智能识别算法，如遗传算法［11］、神经网络［12］、小波变换［13］与数字图像［14］等，但对于超静定次数较多的装配式钢混组合梁均存在识别精度差、噪声鲁棒性不高等问题。

本文基于图像轮廓线叠差分析装配式钢桁-砼组合梁全息变形试验［15］，利用桥梁全息挠度曲线的优势，构造出各特征截面与其他截面之间的挠度影响线关系，依据其奇异值的斜率变化率对桥梁损伤位置及程度进行识别与判断。

1 损伤识别模型及程序设计

1.1 理论模型

准静力作用下桥梁结构变形主要由弯曲引起［16］，结合结构力学虚功原理可知任一点挠度为

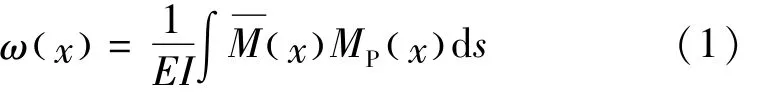
式中：x 为荷载作用位置距原点距离；ω( x )为截面挠度值；EI为结构弯曲刚度；M( x )为单位荷载下虚拟弯矩值；MP( x )为实际荷载下弯矩值。位于该点处挠度曲线的曲率为（见图1，2）

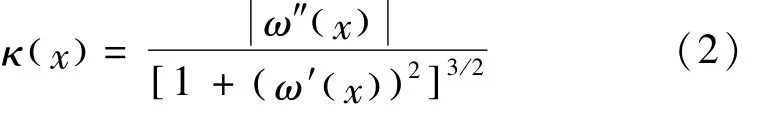
式中：κ( x )为挠度曲线曲率值；ω′( x )、ω″( x )分别为挠度一、二阶导数。

由于式（2）中的挠度一阶导数较小，因此忽略其中高阶项可得：

由材料力学可知，该点处弯矩与挠度的关系式为

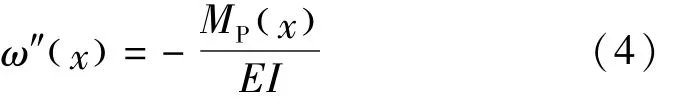
则桥梁结构任意截面处的曲率、挠度、弯矩与刚度之间的关系为

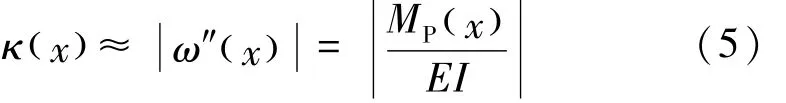
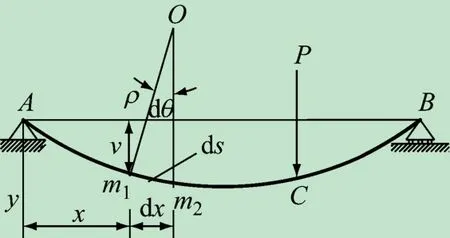
图1 简支梁挠度关系图

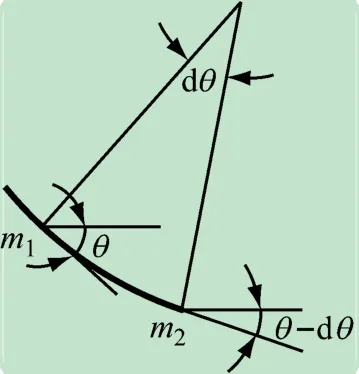
图2 简支梁几何关系图

同理，针对i截面处挠度影响线ωi( x )，依据几何关系得：

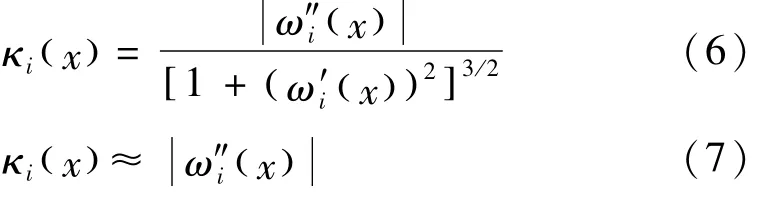
式中：κi( x )为i截面处挠度影响线曲率；ω′i( x )、ω″i( x)分别为i截面处挠度影响线一、二阶导数。

从式（5）与（7）可以看出：桥梁结构状况的改变必然导致刚度的变化，进而影响荷载作用下的挠度与挠度曲线曲率的变化，逆向推导可知结构位移状态可反映桥梁的结构性损伤。因此理论上可以挠度影响线奇异值为基础建立损伤识别模型，从而对超静定次数较多的钢桁-砼组合梁进行结构损伤识别与判断。

在获得静力作用下挠度影响线后，以不同截面影响线列向量之间的协方差构造Hankel 矩阵，具体如下：

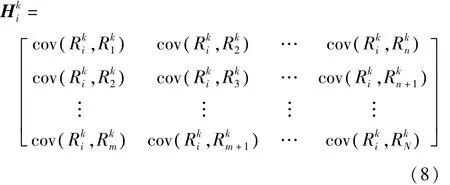
式中：i，j为截面位置数；k 为试验次序；Rki为钢桁梁i号截面处第k次试验所得的挠度影响线列向量；1≤i≤N，1 ＜n ＜N；N 为压缩后的挠度截面序列长度。当m ＝N - n + 1，Hki称为Hankel 矩阵，其行列维数m，n选择规则为

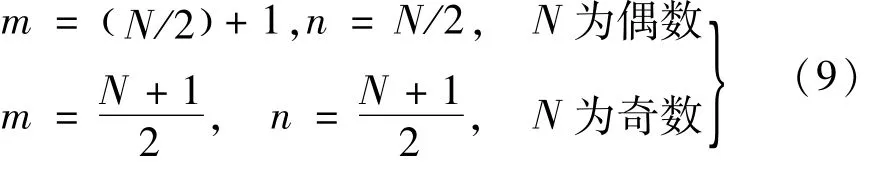
由于Hankel矩阵秩r≤min ( m，n )，因此对其进行奇异值分解（SVD）［17］后利用矩阵欧式范数即可求出各截面挠度影响线奇异信号，其表达式为

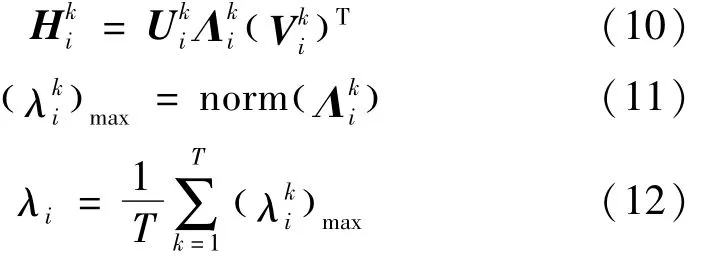
最后利用差分求解步长为h的各截面奇异信号值的一阶导数及其二阶导数为：

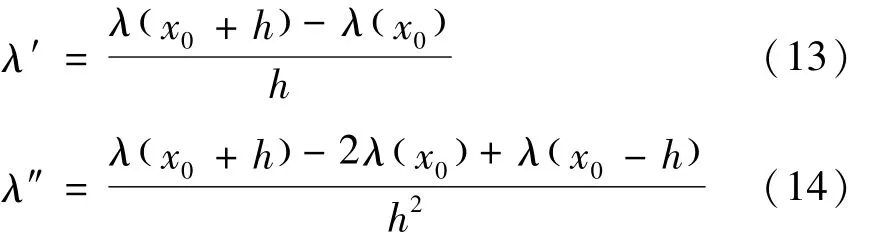
式中：λ′与λ″分别为x0截面处挠度影响线奇异信号第一、二阶导数；h为步长。

由上可知，荷载作用下各截面影响线奇异值大小表征影响线的奇异信号，因此损伤工况的变化导致结构刚度发生转变，超静定结构的应力重分布引起各截面挠度影响线线形变化，进而改变各截面对于特征截面影响线的相关性大小，增加各特征截面奇异值数值并放大损伤信号。

1.2 程序实现

由图3 可知，在获得荷载作用下桥梁的挠度曲线后，首先进行不同荷载位置作用下全截面的挠度数值重组即可获得各特征截面的挠度影响线；进而依次建立各截面与其他截面的相关性并构造Hankel矩阵，在进行SVD后利用矩阵欧式范数即可获取特征截面处的影响线奇异值；最终利用特征截面影响线奇异值与其斜率变化率峰值包含区域与数值大小即可识别损伤位置与程度。

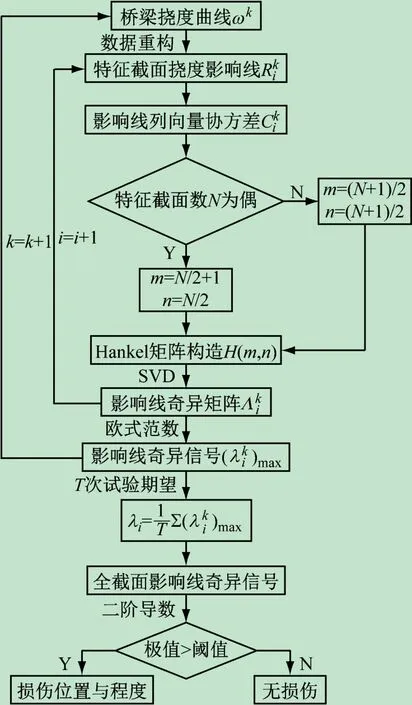
图3 损伤识别算法程序流程图

2 试验梁制作及损伤工况

为验证影响线奇异值的装配式钢桁-砼组合梁损伤识别准确度，以PCSS 剪力键形式联结钢桁架和混凝土的组合梁［18］进行研究。试验梁的制作过程主要可分为桥道板预制、钢桁架拼接、预应力施加以及PCSS剪力键连接四大步骤，其中钢桁架采用Q345 钢材，桥道板为矮肋板式截面且以5 × 1 000 mm + 2 ×1 080 mm长度形式预制，其材料组成为C50 混凝土与HRB335钢筋，剪力联结键中的栓钉尺寸为φ10 mm ×80 mm。钢桁架上下弦截面形式为Π 型，斜杆与竖杆分别采用不同宽度的槽型钢，其具体布置如图4 所示。

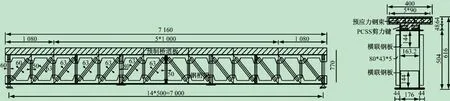
图4 组合梁构造图（mm）

试验过程中加载装置采用可移动式液压千斤顶进行静力加载以获取试验梁特征截面挠度影响线，其加载点顺序见图5，加载过程以分级荷载形式逐渐由0加载到160 kN，两端设置铰支座与滑动支座使组合梁受力模式为简支梁，同时支座处设置横向加劲钢板以防止局部屈曲。

试验过程中，依次对试验梁钢桁斜杆进行对称焊割工作以模拟结构损伤而使杆件失效，其损伤工况施加顺序如表1 所示；图6 所示为组合梁试验图。

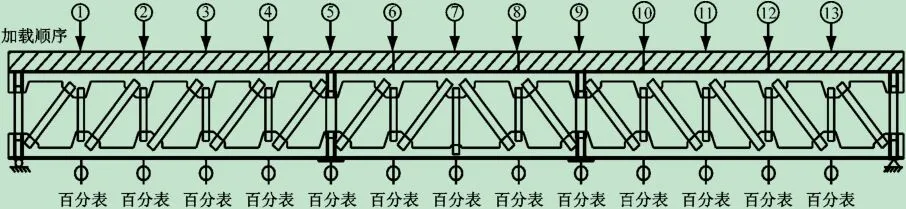
图5 加载顺序与百分表布置图

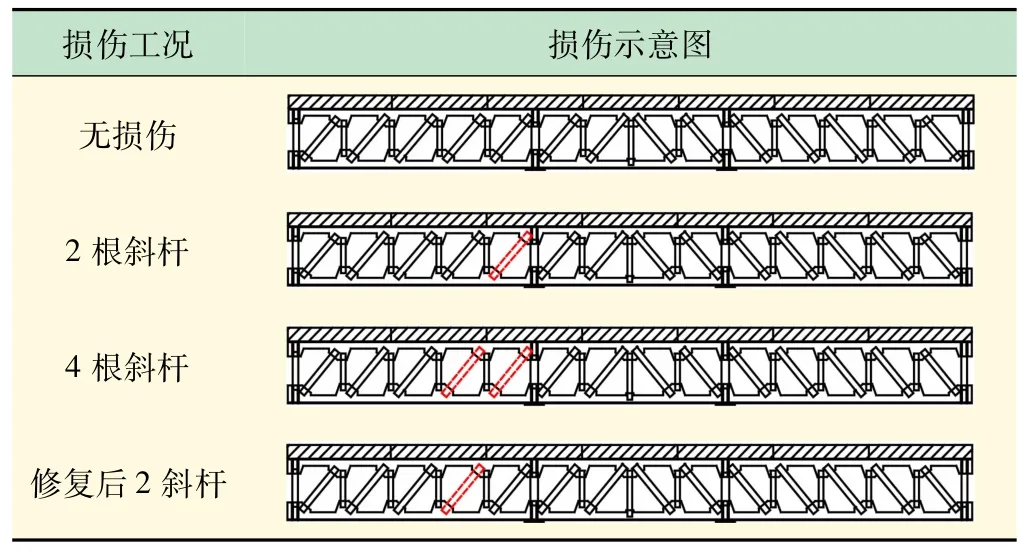
表1 斜杆损伤工况设置

图6 组合梁试验图

试验中主要利用近景摄影技术与结构图像边缘轮廓线叠差技术［15］以获取荷载作用下桥梁挠度曲线，同时设置百分表，对比视觉测量挠度曲线，其无损状态下各荷载位置处试验梁挠度曲线如图7 所示。

3 结果分析

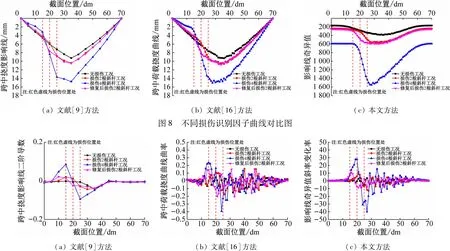
图9 不同损伤识别指标曲线对比图

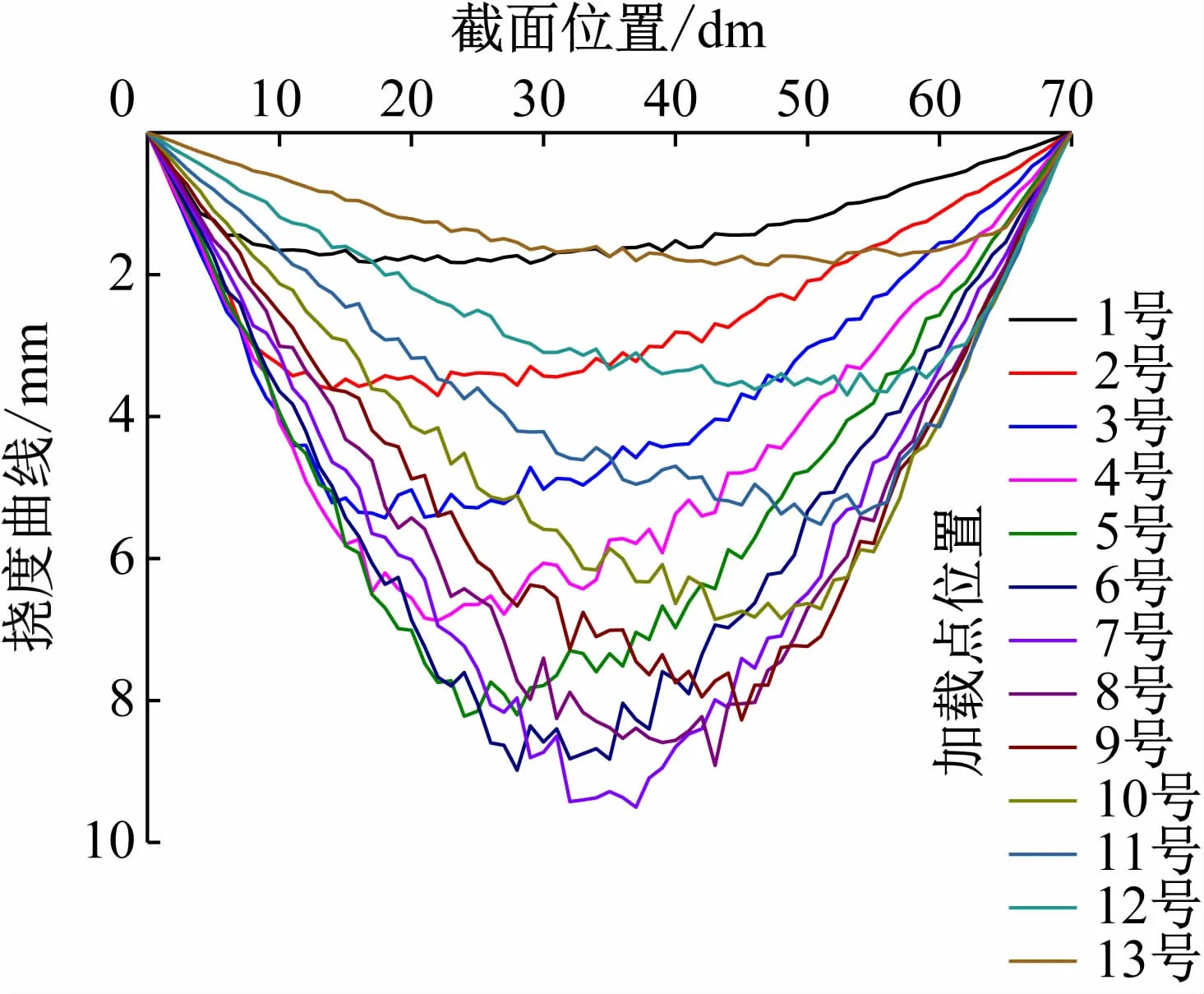
图7 无损状态下不同加载位置处挠度曲线

通过利用不同损伤工况下组合梁挠度数据，依据文献［9，16］及本文基于Matlab 主控程序所编写的损伤识别算法，依次得到基于跨中挠度影响线二阶导数、跨中荷载作用下挠度曲线曲率与挠度影响线奇异值斜率变化率的3 种损伤识别方法结果对比图，如图8 与9 所示。

由于结构自身的刚度状况会随着试验梁损伤工况的改变而变化，进而引起荷载作用下各截面的挠度曲线、挠度影响线和影响线奇异值发生改变，最终使各损伤识别指标曲线呈现一定的规律性。对比图8 可知，文献［9］中所含损伤识别指标点数较少，由于试验过程中只进行13 次加载，因此曲线所包含的桥梁结构状态信息与局部形变信息的完整性较低，曲线的误差累计较大；从文献［16］中的损伤识别因子-特征截面挠度曲线中可以看出，不同损伤工况下各曲线的趋势有一定变化，但差异不明显，主要原因可能在于高次超静定结构发生局部损伤时的应力重分布区域较广；对比分析损伤识别因子曲线图可知，不同工况下影响线奇异值曲线图差异明显，随着斜杆损伤根数增多，奇异值数值整体增大，且增长程度远大于斜杆损伤根数；由损伤位置分别位于20 ～25 dm与15 ～20 dm的两种损伤工况奇异值图可知，其曲线大致向左顺移10 dm左右，因此通过对比奇异值整体数值即可对损伤定性。

由图9（a）可知，处于无损状态下跨中突变峰值（最小值）接近损伤2 根斜杆工况的突变峰值，理论上无损状态下该曲线值为0，其原因主要来自于测量误差，因此该方法无法准确判断出跨中损伤；同时来自跨中的噪声信号会影响临近区域截面处的突变峰值，减小其他位置处损伤峰值绝对值甚至损伤定性，从而引起损伤位置与程度的误判，且其识别指标的数值大小决定了该方法对于挠度的测量精度要求很高。综上分析可知其抗噪能力与识别灵敏度较低。观察图9（b）中损伤识别指标数值，在损伤2 根斜杆工况下的跨中荷载挠度曲线曲率中出现多处未损伤区域数值超过损伤区域极值；理论上未损伤区域的识别指标数值也应为0，但指标数值波动幅度大，且曲线中未损伤区域数值收敛性及抗噪性较差，如表2 所示，对于损伤2 根斜杆两种工况的位置识别准确度为0，因此该方法对于钢桁-砼组合梁的损伤位置识别准确性相对较低。由图9（c）可知不同损伤工况下试验梁识别指标最大峰值突变点与损伤位置大致相同，即使处于损伤工况下超静定结构发生内力重分布，该指标也能大致识别出损伤位置；对于损伤2 根斜杆工况的不同位置处，峰值突变位置和大小与损伤区域和程度相近。无损状态时试验梁曲线趋势相对平缓且在0 值附近波动，符合理论推导。对于4 种不同损伤工况曲线可知，峰值突变点随损伤程度加大而增加，同时离损伤区域越远的截面其值逐渐收敛于0，证明该方法对于钢桁-砼组合梁的损伤识别鲁棒性与抗噪性较强，对于桥梁损伤位置与程度的判定具有较高准确度。

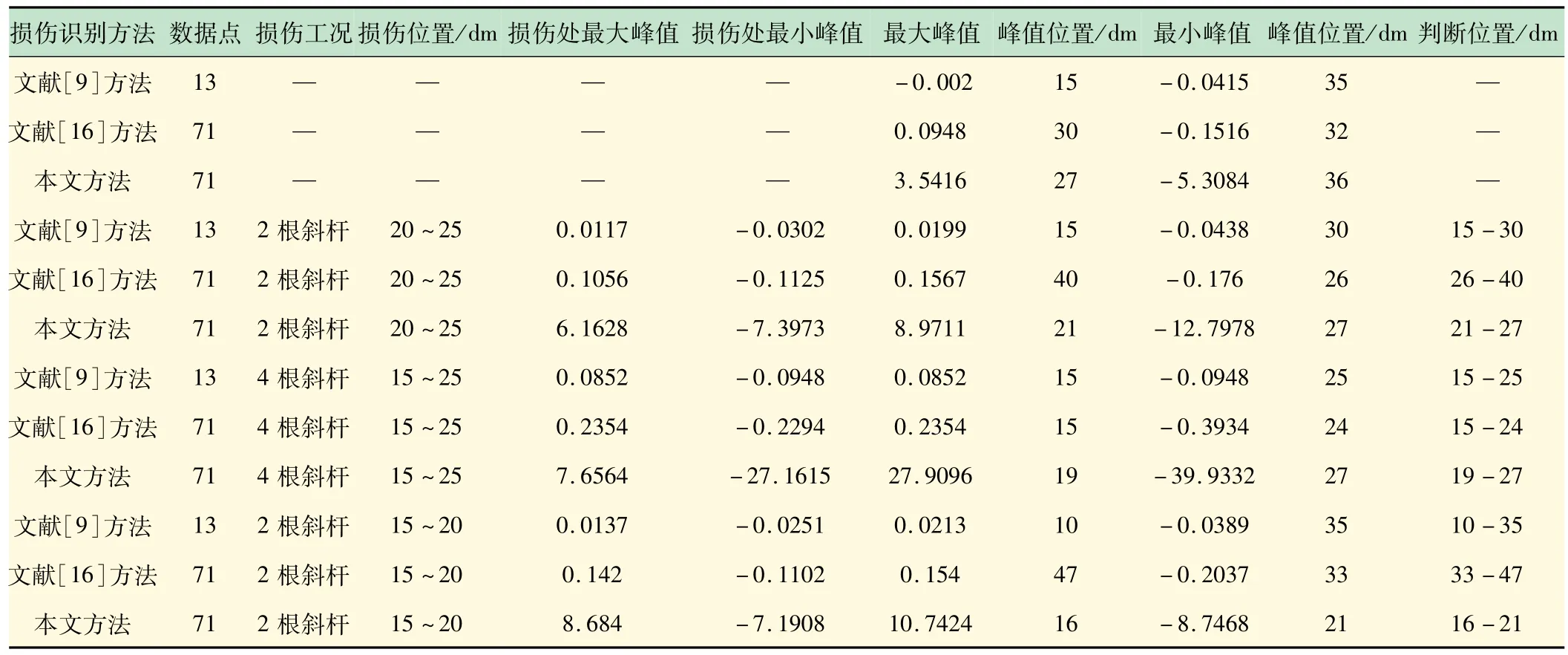
表2 不同损伤工况下损伤识别指标表

4 结 论

本文利用挠度影响线奇异值为损伤识别因子，以其斜率变化率为损伤识别指标，完成了对一片装配式钢桁-砼组合梁进行多种损伤工况下的试验研究，结论如下：

（1）利用影响线奇异值作为损伤定性指标，结合斜率变化率最大峰值出现位置与数值大小作为损伤定位与定量指标，能够有效识别判断出不同损伤工况下组合梁的损伤位置与程度，同时放大损伤信号。

（2）对比多种损伤识别方法结果图，本方法的损伤位置识别准确度高，其峰值位置基本对应损伤位置且均适用于试验的3 种损伤工况，侧面验证了基于挠度影响线奇异值的损伤识别模型与算法程序针对试验数据的抗噪性能。

（3）依据本文损伤识别算法，结合桥梁结构数字影像数据与图像处理技术，在通过日常监控视频获得的挠度曲线精度满足要求的情况下，有望实现荷载作用下实际桥梁的非接触式实时自动无损健康监测。