内插中心斜杆换热管的换热性能

王小雨，张聿祥

(江汉大学 智能制造学院，湖北 武汉 430056)

能源问题不仅关系到人民生活质量和生态环境发展，还事关国家经济安全和战略安全，其早已成为经济社会发展的重要问题之一[1]。如何提高能源的利用已成为至关重要的问题，人类对能源的利用过程绝大部分都涉及到热能的传递和转化。换热器是进行热交换的设备，提高换热器的换热性能对节能具有重要意义。换热管是管壳式换热器的基本组成单元，是实现换热过程的关键组件。为了提高换热器的换热性能，许多学者对换热管内流体的流动和换热性能展开了研究，并形成了丰富的强化传热技术体系。根据是否需要提供除泵功之外的附加动力，将强化传热技术分为主动强化、被动强化以及两者相结合的复合强化[2]。主动强化技术因需要增加设备，使系统变得更加复杂且投资成本增加，在工业中的使用受到了限制。被动强化传热技术旨在修改传热表面的结构或者在流体中增加扰流元件来扰动流体和提高传热性能，因其系统简单、制造成本低、可靠性高等优点在工业中具有更广泛的应用。

被动强化传热技术主要从三个方面展开，即管型改变[3-4]、管壁处理[5-7]和内插扰流元件[8-13]。其中内插扰流元件是一种常见的管内被动式强化传热技术，该技术通过在管内插入不同结构的扰流元件来扰动流体，改变通道内流体的流动结构，促使管内形成纵向涡或二次流，从而减薄或破坏热边界层[14-17]。相比其他传热技术，该技术具有加工简单，制造成本低，可直接对旧设备进行改进，且易于维护等优点。常见的扰流元件有扭带[8]、螺旋片[9]、涡发生器[10]、多孔介质[11]、小管插入物[12]、波浪带插入物[13]等，它们各自有相应的优缺点，适用于不同的场合。

周璐瑶等[18-19]提出了一种纵向涡流强化管(内插中心斜杆)的换热管，研究了斜杆长度、斜杆倾角和杆长对换热性能的影响。通过模拟发现这种类型的管插入件可以使流体形成具有多个纵向涡流的涡流结构，并且可以在阻力增加不太大的前提下，有效提高换热能力。通过内插中心斜杆将管内流体分为6个周向对称的流动区域，在每个区域中形成了一个纵向旋流的涡结构，中心斜杆使管内形成了多纵向旋流的流动结构。因此，内插中心斜杆的换热管能够获得优异的强化传热性能。

但内插中心斜杆的数目和直径等参数对换热管的换热性能的影响，尚未有学者进行研究，因此，本文讨论了斜杆数目、节距、直径等参数对内插中心斜杆换热管换热性能的影响，以期进一步优化内插中心斜杆的几何结构，对内插中心斜杆换热管的换热性能研究起到一定的指导意义。

1 光管的数值模拟及验证

图1 光管的网格划分Fig.1 Mesh generation of the smooth tube

1.1 光管的参数设置

本文所选管内介质为水，20 ℃的物性参数为：ρ=998.2 kg/m3，μ=1.003×10-3kg/(m·s)，CP=4 182 J/(kg·K)和λ= 0.6 W/(m·K)；光管管长为L=500 mm，管内径为di=20 mm，网格划分如图1所示。

1.2 控制方程与假设

换热管的模拟要满足3个基本方程：质量守恒方程即连续性方程、能量守恒方程和动量守恒方程。具体公式参考文献[20]。

为了便于模型的建立和计算，做出以下简化：(1)忽略中心倾斜杆插入元件的热传导和换热管壁厚；(2)流体的物理参数为固定值;(3)流体是一种连续不可压缩、不考虑重力、没有黏性耗散、各向同性牛顿流体；(4)热辐射和重力的影响予以忽略。

1.3 边界条件与计算方法

采用Fluent进行计算时，选择3D、稳态和基于压力的隐式求解器。管的内壁采用2 000 W/m2的恒定热通量密度，并定义为无滑壁面；中心斜杆扰流元件的表面为绝热无滑壁面。在管道出口处采用自由出流边界。湍流模型选择标准的κ-ε模型，计算时采用SIMPLE算法，选择基于最小二乘单元的梯度，压力选择二阶格式，动量和能量采用二阶迎风格式，湍流动能和湍流耗散选择一阶迎风格式。

1.4 网格无关性验证

使用Fluent软件数值模拟计算出努塞尔数与网格数的关系。如图2所示，在一定数量网格内努塞尔数变化波动较大，但随着网格数量的增加努塞尔数趋于平稳，模拟结果显示在五十万的网格数后努塞尔数变化明显较小，因此在后续的数值模拟中，出于电脑计算效率与能力问题，最终选择五十万以上的网格数量。

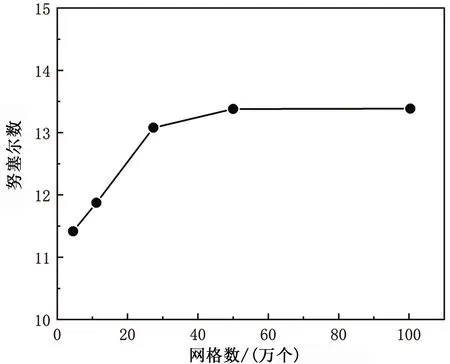
图2 网格数量与努塞尔数的关系Fig.2 Relation between the mesh number and Nusselt number

1.5 光管的经验公式计算值与模拟对比

为了验证数值计算结果的可靠性，将光管模拟得出的努塞尔数和压降与经验公式计算的值进行比较。

因为管道的直径设置得比较小，同时流体与壁表面之间的温差也比较小，当流体的μ/p值比较大时，自然对流对强制层流传热的影响可以忽略不计。此时，对流传热系数可以使用西德尔(Sieder)和塔特(Tate)关联式(1)计算：

(1)

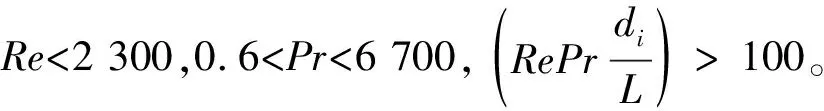
压降经验公式如下

(2)

式中：Δpf为因克服阻力而引起的压力降，Pa；hf为能量损失，J/kg；λ为导热系数，W/(m·℃) ；u为流体流速，m/s。

在介质流速为0.07、0.08、0.09、0.10 m/s时，经验公式计算的努塞尔数和压降与模拟值的比较分别如图3和图4所示。

图3 光管努塞尔数的模拟值与经验公式计算值对比Fig.3 Comparison between simulated and calculated values of empirical formula on the Nusselt number of the smooth tube

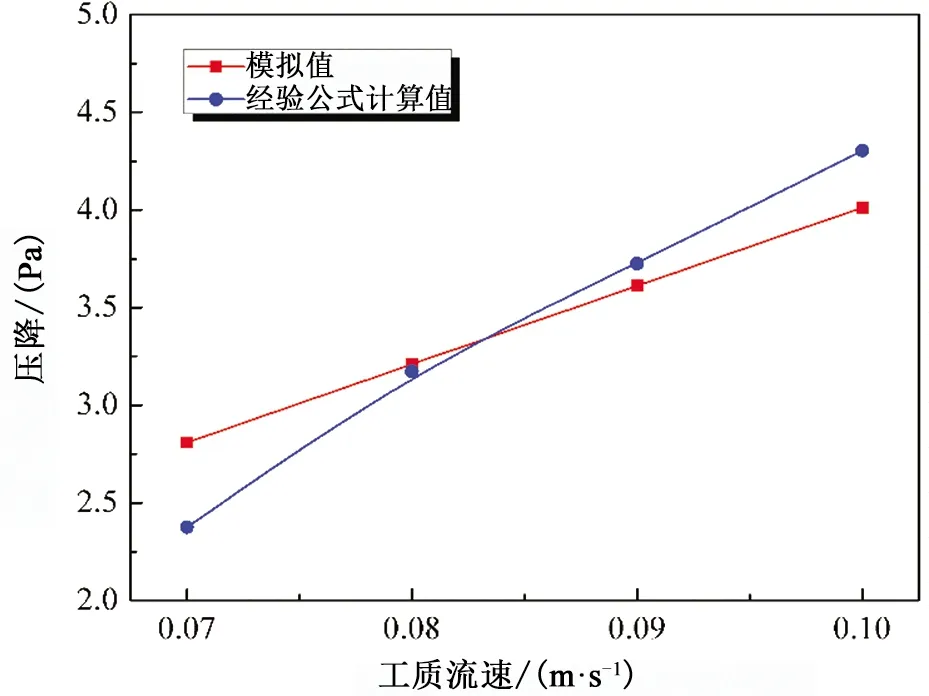
图4 光管压降的模拟值与经验公式计算值对比Fig.4 Comparison between simulated and calculated values of empirical formula on the pressure drop of the smooth tube

2 内插中心斜杆换热管的模拟

内插中心斜杆的换热管是一种纵向涡流强化管，可以明显改善管内热量的传递。为了研究不同结构尺寸的中心斜杆换热管对换热性能的影响，本文选取了中心斜杆的三个几何参数，即倾斜杆的数量(n=2、3、4、5、6)，节距(p=20、25、30、35、40 mm)和连杆的直径(d=1.0、1.5、2.0、2.5、3.0 mm)，作为研究对象，分别探讨了各参数对努塞尔数和压降的影响。

2.1 中心斜杆几何建模和网格划分

本文设计的中心斜杆的几何结构如图5所示。倾斜的中心连杆由直径为2 mm的小连杆组成，这些连杆沿圆周对称地倾斜，倾斜角为30°并以相等的间隔布置在中心2 mm直径的连杆上。在模拟中，将换热管的几何参数选择为管的长度L=500 mm，管的内径di= 20 mm。

图5 中心斜杆的几何模型Fig.5 Mode of the central inclined rod

2.2 结果分析

通过Fluent后处理，得出内插中心斜杆换热管圆截面温度分布云图(图6)，可以看出中心斜杆对于流体的混合热交换有很大的帮助，因为流体受到中心斜杆的阻碍后，被引导后有一个径向的矢量，会与靠近管壁的高温流体层进行冲刷混合，从图中比较容易看到高温层明显变薄。图7为管壁温度分布，可以看出中心斜杆的扰流对打破边界层有一定作用。

图6 内插中心斜杆换热管圆截面温度分布云图Fig.6 Temperature field of the central inclined rod tube in the circular section

图7 内插中心斜杆换热管速度分布云图Fig.7 Velocity field of the central inclined rod tube

图8为内插中心斜杆换热管圆截面速度分布云图，可以看出因中心斜杆的扰流产生的流体轨迹，十分符合文献[14]所展示的状态，靠近斜杆的区域速度相对较高，向其他区域有辐射。偏红色区域就是因为中心斜杆的结构对流体产生了旋流，这对于冷、热流体混合有很大帮助。从图9可以看到在斜杆后还是存在有一定的运动死区。由此可以初步推断如果过多地设置斜杆数量，或者是过大地设置中心连杆上的斜杆直径会使这种运动死区增大，对于流体流动以及冷热流体混合都有负面影响。

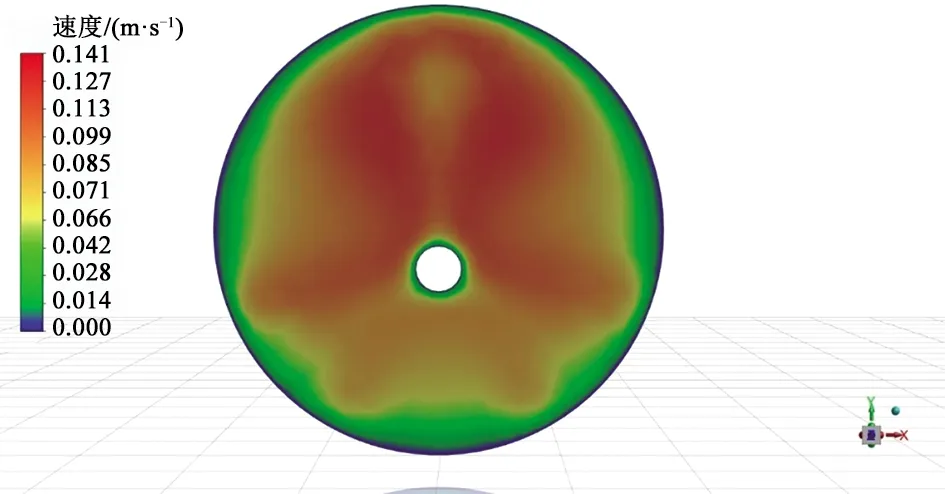
图8 内插中心斜杆换热管圆截面速度分布云图Fig.8 Velocity field of the central inclined rod tube in the circular section

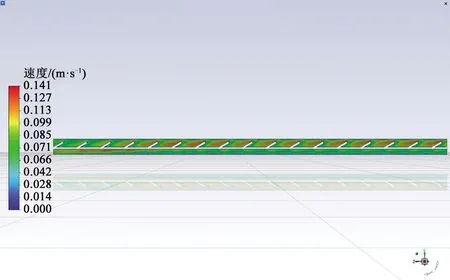
图9 内插中心斜杆换热管速度分布云图Fig.9 Velocity field of the inserted central inclined rod tube

3 内插中心斜杆换热管几何结构的研究

3.1 斜杆数量对内插中心斜杆换热管性能的影响

对改变斜杆数量后换热管的换热性能进行分析，得到了努塞尔数和压降随斜杆数量的变化关系，如图10所示。从图中可以看出，在2到5个斜杆时，换热系数是不断增大的，这是由于通过斜杆进行扰流，使得流体在径向空间发生冷热流体的混合，更好地进行热交换；但是当斜杆数量增加到6时，这时的努塞尔数开始下降，结合其压降的激增，可以推断是因为阻挡物过多，而形成了较多的流动死区，导致换热系数无法进一步提高，甚至开始下降。因此为了提高换热系数不能一味地增加其斜杆数量，应选择适当的数量。从图10中也可以看出，随着斜杆数量的增加，其进出口端面的压降也一直在增加，说明增加斜杆数量虽然可以一定程度增大换热系数，但其带来阻力的负面影响也在随之增大。

内插中心斜杆换热管的换热性能主要受到努塞尔数和压降的影响，为了综合评价两者对换热管综合换热性能的影响，采用了文献中广泛认可的性能评价指标IPEC[21-22]来研究二者的影响，计算公式如式(3)所示：

(3)

其中，Nu为内插中心斜杆换热管努塞尔数，Nus为光管努塞尔数，f为内插中心斜杆换热管阻力系数，fs为光管阻力系数。

图11为斜杆数量对内插中心斜杆换热管综合换热性能的影响，由图11可知，随着斜杆数量的增加，综合换热性能下降，但是内插中心斜杆换热管的综合换热性能始终大于光管的换热性能(IPEC>1)。本文斜杆数量为3时，内插中心斜杆换热管的综合换热性能较好。

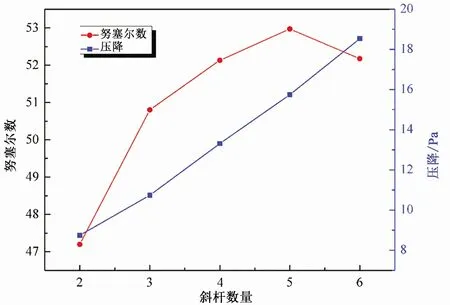
图10 斜杆数量对内插中心斜杆换热管换热性能的影响Fig.10 Variation in heat transfer performance with the number of inclined rods

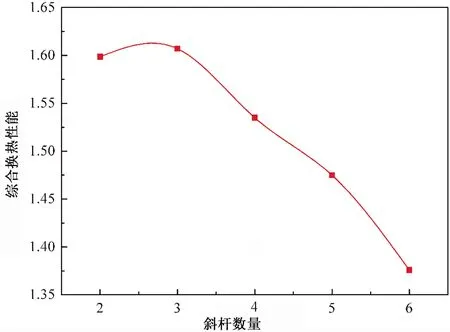
图11 斜杆数量对内插中心斜杆换热管的综合换热性能的影响Fig.11 Variation in IPEC value with the number of inclined rods

3.2 斜杆节距对内插中心斜杆换热性能的影响

对改变斜杆节距后换热管的换热性能进行分析，得到了努塞尔数和压降随斜杆数量的变化关系。从图12中可以看出，随着斜杆节距的增加，其努塞尔数和压降随之减小。这是因为斜杆节距增加后，斜杆对流体的扰流作用降低，而流体的扰流会有助于温度的传递。因为斜杆节距的增加，使得流动阻力减小，故而压降降低。

图13为斜杆节距对内插中心斜杆换热管综合换热性能的影响，由图13可知，随着斜杆节距的增加，综合换热性能下降，但是内插中心斜杆换热管的综合换热性能始终大于光管的换热性能(IPEC>1)。本文斜杆节距为20 mm时，内插中心斜杆换热管的综合换热性能较好。

图12 斜杆节距对内插中心斜杆换热管换热性能的影响Fig.12 Variation in heat transfer performance with the pitch of inclined rods

图13 斜杆节距对内插中心斜杆换热管的综合换热性能的影响Fig.13 Variation in IPEC value with the pitch of inclined rods

3.3 斜杆直径对内插中心斜杆换热性能的影响

对改变斜杆直径后换热管的换热性能进行分析，得到了努塞尔数和压降随斜杆数量的变化关系，如图14所示。从图14可以看出，增大中心斜杆的直径对于传热有一定帮助，努塞尔数随着斜杆直径的增大也逐渐变大，特别是从1.0 mm到1.5 mm时其传热性能有一个突变的激增，而从1.5 mm到3.0 mm时变化较为平缓。又因为随着斜杆直径的增大，其带来的压降也随之增加。故斜杆直径不宜过大或过小。

图15为斜杆直径对内插中心斜杆换热管综合换热性能的影响，由图15可知，随着斜杆直径的增加，综合换热性能先上升后下降。在斜杆直径为1.0 mm时，内插中心斜杆换热管的综合换热性能小于光管的换热性能(IPEC<1)。但当斜杆直径大于等于1.5 mm时，内插中心斜杆换热管的综合换热性能大于光管的换热性能(IPEC>1)。本文斜杆直径为2.0 mm时，内插中心斜杆换热管的综合换热性能较好。

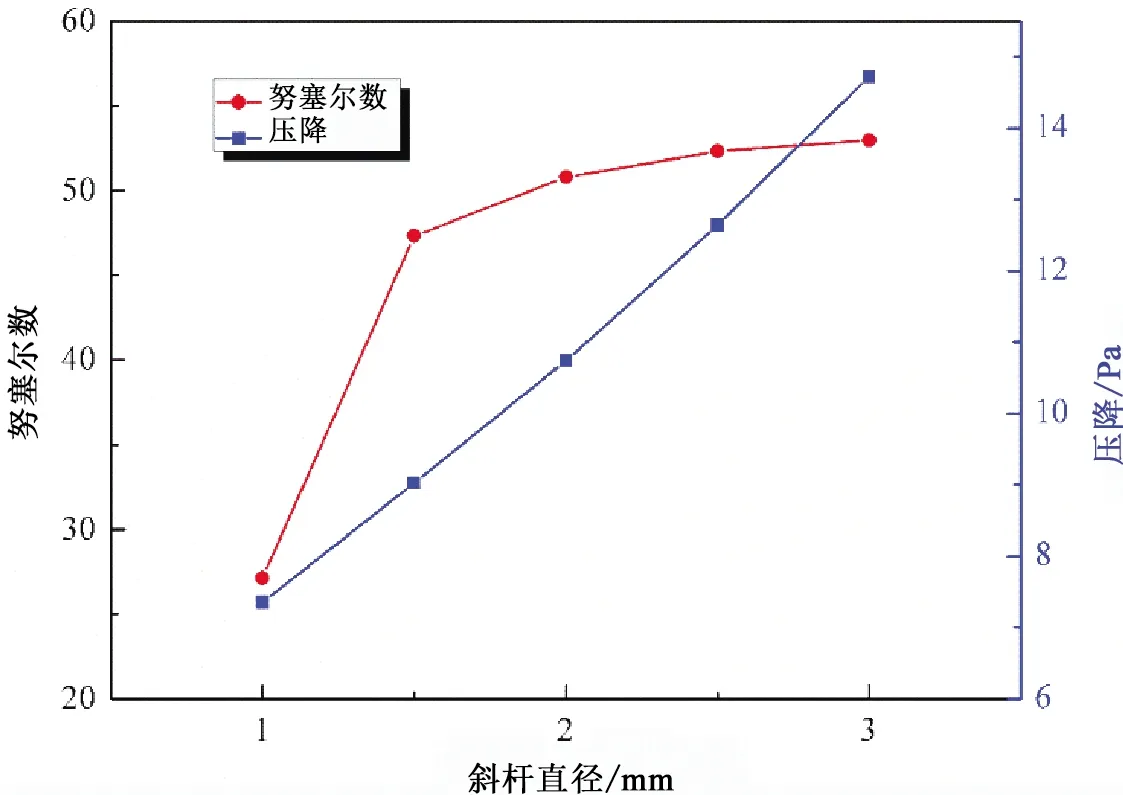
图14 斜杆直径对内插中心斜杆换热管换热性能的影响Fig.14 Variation in heat transfer performance with the diameter of inclined rods

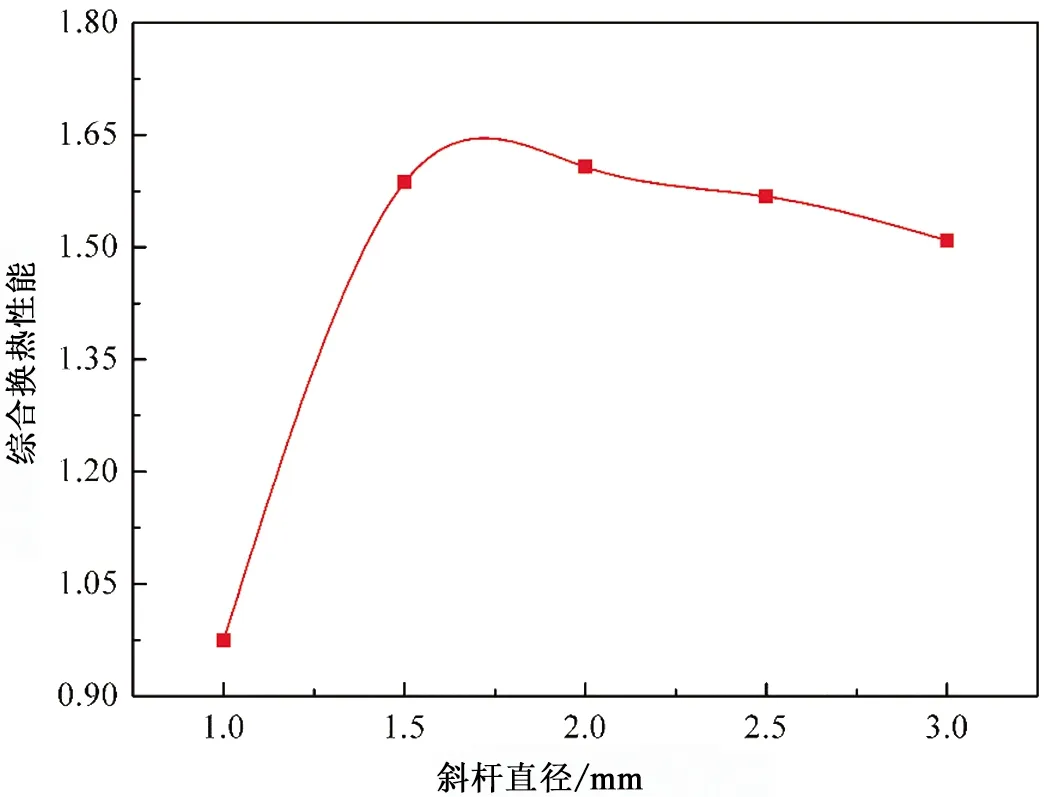
图15 斜杆直径对内插中心斜杆换热管的综合换热性能的影响Fig.15 Variation in IPEC value with the diameter of inclined rods

4 结论

本文主要探讨了斜杆几何机构对内插中心斜杆换热管换热性能的影响，根据模拟结果得出以下结论：

(1)通过综合换热性能的比较，发现除斜杆直径为1.0 mm时，内插中心斜杆换热管的综合换热性能略低于光管(IPEC<1)，其余参数下的内插中心斜杆换热管的综合换热性能都优于光管(IPEC>1)，且综合换热性能较光管提高了50%以上。

(2)在斜杆数量为2到5时，其努塞尔数是不断增大的，但是当其斜杆数量增加到6时，这时的努塞尔数开始下降。本文通过对内插中心换热管综合性能的分析得出斜杆数量为3时，内插中心斜杆换热管的综合换热性能较好。

(3)随着斜杆节距的增加，其努塞尔数随之减小，流体阻力减小，压降降低。对内插中心斜杆换热管斜杆节距的综合换热性能分析得出，斜杆节距为20 mm时，内插中心斜杆换热管的综合换热性能较好。

(4)增大中心斜杆的直径对传热有一定帮助，努塞尔数随着斜杆直径的增大也逐渐变大，特别是从1.0 mm到1.5 mm时其传热性能有一个突变的激增，而从1.5 mm到3.0 mm时变化较为平缓。故斜杆直径不宜过大或过小，本文对内插中心斜杆换热管斜杆直径进行综合换热性能分析得出斜杆直径为2.0 mm时，内插中心斜杆换热管的综合换热性能较好。