空间失稳目标线阵雷达成像机理及三维重建

李荣华，薛豪鹏，杨友庆，李 恒

(1. 大连交通大学机械工程学院，大连 116028；2. 上海航天技术研究院，上海201109)

0 引 言

随着人们对空间探索的不断深入，地球外太空中的航天器、太空碎片以及太空垃圾正在不断增加，使得空间环境日益恶化[1]。研究空间失稳目标的在轨测量与操纵技术刻不容缓，解决问题的关键就是准确得到目标运动情况以及位姿信息[2-3]。由于空间失稳目标的非合作特性使得不能利用合作标识以及星间数据传输进行位置姿态信息的确定[4]，Sharma等[5]采用单目视觉进行飞行器位姿测量，由于深度信息的缺少，需要假设特征点坐标已知；Li等[6]采用双目相机实现卫星太阳能帆板的特征提取与相对位姿测量，但由于双目视觉对目标表面纹理特性依赖程度很高，且测量精度受光照条件等因素限制而只适用于近距离的交会对接测量[7]；相比于可见光测量手段，三维成像激光雷达系统不仅能够捕获被测目标的强度像还能提供目标的距离图像，能够获取更为丰富的目标信息，且不受光照条件限制[8]。激光成像雷达分为线阵扫描型和面阵扫描型两种，面阵式雷达的优点是可以快速扫描视场中的目标，但面阵式非扫描型激光雷达难以实现高分辨率，大视场角测量，对目标的测量精度不能满足要求，线阵式激光成像雷达由于受限制因素少、抗干扰能力强等优点在空间失稳目标测量应用上的需求越来越迫切[9]。

目前欧洲航天局(The European Space Agency)提出使用万向节作为扫描机构，实现了20°×20°的扫描角度，成像帧频不小于1Hz[10]；美国国家航空航天局NASA正在研制LIST(LiDAR surface topography)雷达系统[11]，其采用1000像元的光子计数探测器方案，将能够实现5 m的横向分辨率和分米级的测距精度；国内王盈等[12]提出一种复杂空间目标的在轨激光雷达成像仿真流程，并强调面积法在目标成像可见判断方面的适用性；孙日明等[13]提出一种基于准线的可视点云判别算法，并对特征采集完整性进行参数优化，但所提取的可测点云信息中存在较多的错误点，扫描数据获取效率较低。方元坤等[14]为实现分布式遥感系统星间相对状态的精确确定提出一种基于MEMS激光雷达与纳型星罗盘的星间相对状态估计方法；陈凤等[15]为了通过目标探测识别获得空间目标三维结构等更多在轨信息，研究了基于序列图像的三维重建方法，并可以提供帆板天线等部位的结构信息；蔡晗等[16]提出一种基于几何特征综合匹配的双目超近距相对位姿视觉测量方法，精度受光线影响，不完全适合基于激光雷达信息的运动估计；杨洪飞等[17]针对空间目标的宽动态范围提出了一种多次曝光的图像融合方法，开展了空间目标模拟成像试验，采用融合的图像对目标三维重建；张珂殊等[18]提出了一种基于距离向扫描的SAL(Synthetic aperture laser，合成孔径激光雷达)目标三维重建方法，通过距离向扫描体制SAL得到一定扫描角度范围内的多条合成孔径图像，利用相邻图像目标的重叠成像实现三维重建；但是并没有进行重建目标整体重建精度以及重建质量的分析。

本文针对基于点云的空间目标三维重建研究中前期理论探究的仿真线阵雷达扫描结果获取以及动态目标三维重建精度低、速度慢等问题，开展空间失稳目标线阵雷达成像机理及三维重建研究。提出双切片法的空间失稳目标可见点云提取方法，提高目标可视部位点云提取精度及效率。同时研究不同视角下多幅点云三维重建及重建结果评价机制，采用ICP(Iterative closest point，最近迭代点)配准方法进行目标位姿增量信息求解，通过逆序重建方案，分析数据冗余对重建结果的影响，按照任务指标要求建立重建点云精度与点云平均密度评价体系，分析比较得出满足指标要求的最佳方案，最后进行仿真实验，检验了方案的准确性。

1 空间失稳目标运动机制

1.1 坐标系建立

目标坐标系(XO-YO-ZO)：其原点为待测目标的几何中心；XO轴方向为太阳帆板中线方向；YO轴方向为待测目标自旋轴方向，即垂直于太阳帆板的目标主体中轴线方向；基于右手法则确定ZO轴方向为垂直于目标本体平行于帆板。

雷达坐标系(XL-YL-ZL)：原点坐标建立在雷达中心，其XL，YL，ZL三轴方向与初始获取目标反馈信息的方向一致。

世界坐标系：与雷达坐标系重合。激光雷达绕飞半径：60 m。各坐标系之间的关系如图1所示。

图1 扫描工况坐标系

1.2 目标运动模型

空间失稳目标的运动主要分为三种形式，即目标绕自身旋转轴的自旋、目标整体绕章动轴旋转的章动以及进动，由于线阵激光雷达扫描速度快，因此仅考虑目标的自旋运动与章动运动。且自旋运动与章动运动都是匀速的。如图2所示，H轴为章动轴，Yb为自旋轴。

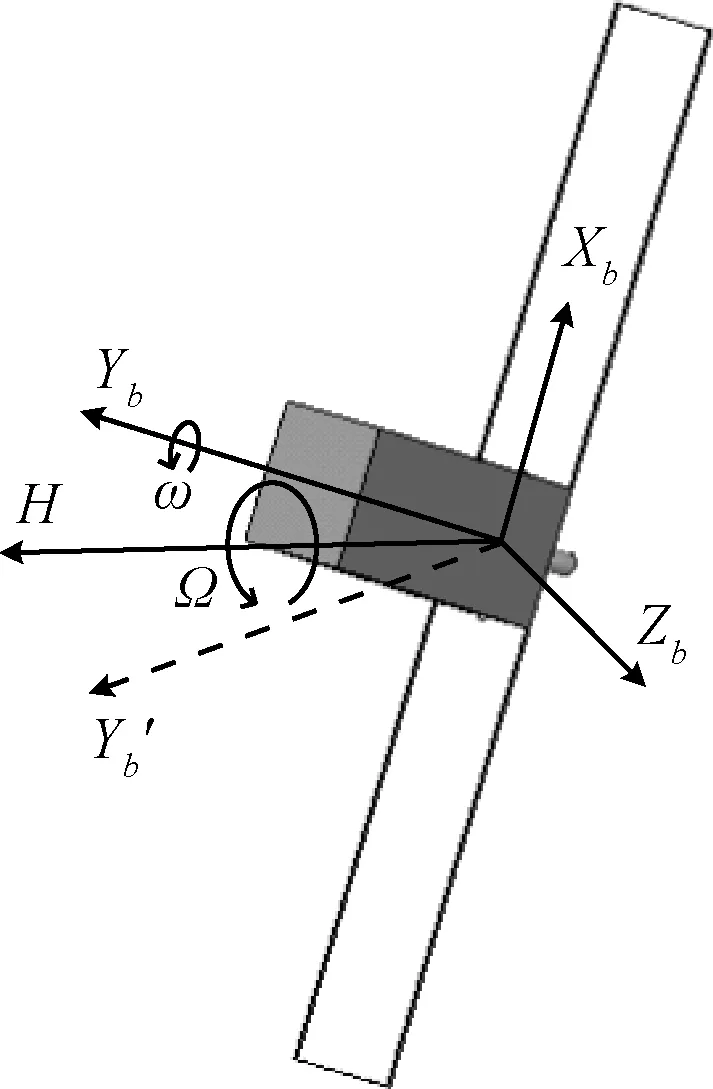
图2 空间失稳目标运动模型图

2 线阵激光雷达扫描成像机理

根据线阵式激光雷达扫描成像原理，提出具有一般性的线阵扫描型激光雷达成像点云获取方法，通过分析雷达扫描驻流观测方式、可见点提取机制、成像分辨率以及成像噪声的添加等对空间失稳目标进行成像建模。具体流程如图3所示。

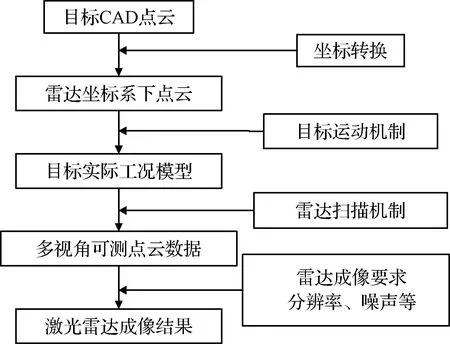
图3 雷达成像机理仿真流程图

2.1 雷达扫描方式

如图4所示，模拟激光雷达对目标进行360°多视角扫描成像，失稳目标按照一定的自旋速度与章动速度进行运动，激光雷达按照固定帧频进行可视点数据采集，每次扫描均为固定线阵宽度的往复式扫描，得到不同时刻对应的失稳目标可测部位点云数据。

图4 激光雷达驻留观测机位示意图

2.2 双切片法可见点提取机制

以目标点云数据坐标值作为判定条件，采用双切片法的可测点提取机制，进行多视角可视数据提取。

由于激光雷达视线方向为Z轴负方向，首先对雷达坐标系下的目标点云沿X轴方向进行切片，得到沿X轴切片的环状点云，即YOZ坐标平面的点云数据；其次将点云数据按照Y坐标值大小排列，理论上在相同的Y坐标值点集中，Z坐标值最大的点即为可视点。但是由于目标原始点云的属性，按照此种判别方式进行提取时会出现大量的误判点。因此将Y坐标值在一定阈值范围内的点切为一个判断点组，再提取其中的Z坐标值最大点为可视点，同时可根据目标点云属性以及成像分辨率等要求进行阈值大小的调整。提取过程如图5所示。

图5(a)表示激光雷达沿视线方向依次进行线阵扫描，每一次线扫所提取的环状待可测区域判别的点云如图5(b)所示，根据目标点云的特征，对各点Y坐标进行阈值设定，图5(c)表示的是按照阈值大小对符合判断条件的点进行处理，最后得到的每一次线阵扫描提取的可见点信息如图5(d)所示。

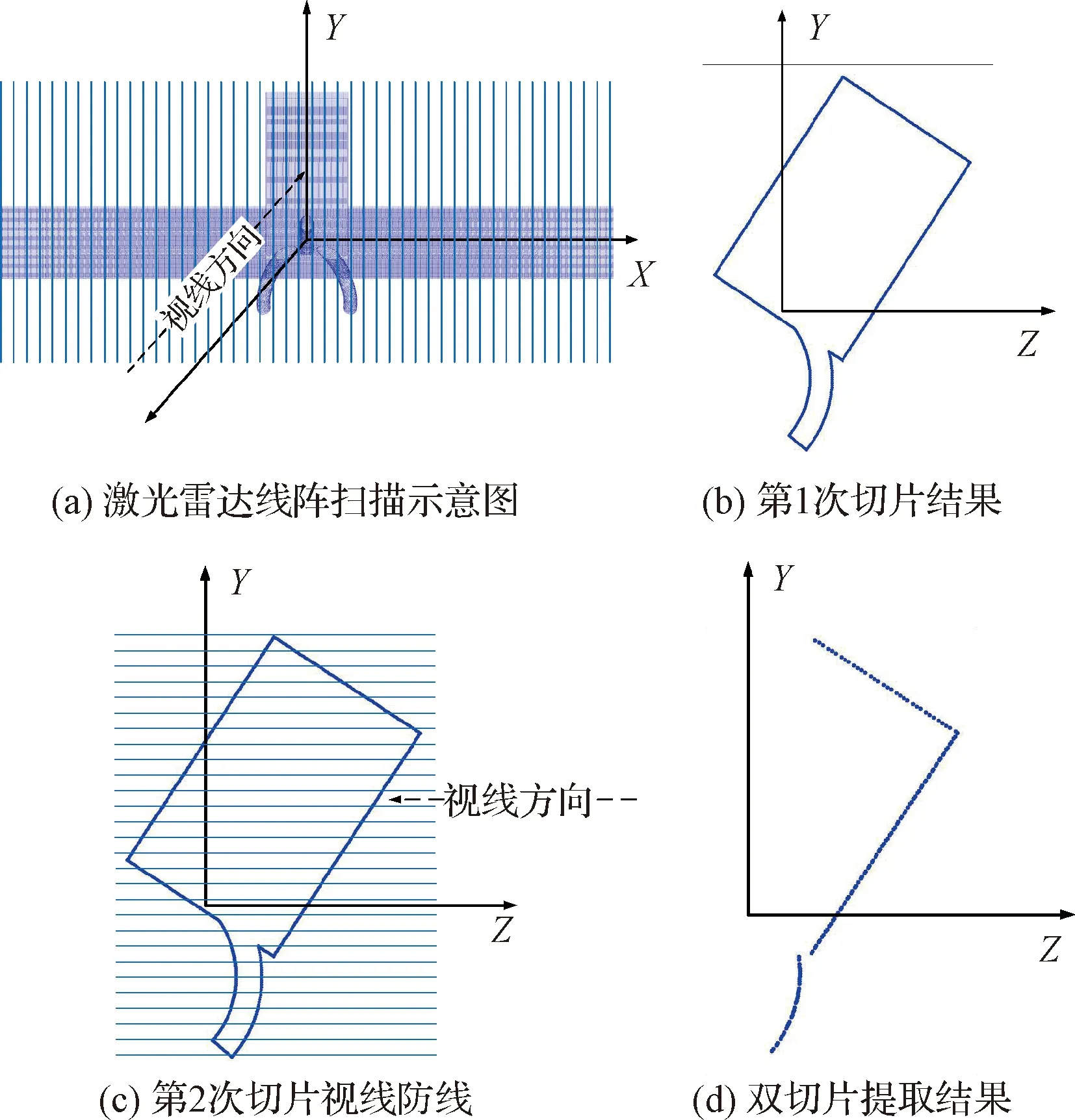
图5 可见点判别方法示意图

2.3 扫描数据生成

空间任务中激光雷达成像结果受多方面的影响，如激光光源、稳定性、接收机噪声、目标场景反射特性等[19]。散斑效应是影响目标细节成像的一个重要因素，影响成像清晰度。接收机噪声产生的主要原因是探测器噪声、各放大器噪声等，一般为高斯加性噪声。根据任务中的工况要求，本文只考虑接收机噪声以及散斑效应两方面因素对成像带来的影响，建立相应的噪声等效功率模型，并根据所建立的噪声模型对成像点云进行加噪处理，得到仿真激光雷达成像结果。噪声等效功率模型分析如下：

(1)

式中:Pr,speck为散斑效应的回波功率；Et为接收机噪声规律；并且满足

(2)

式中:SS为散斑效应的噪声强度，与散斑个数M、随机变量均值S、光学系统孔径和散斑的大小等相关[13]，Pr为理想状态下的回波功率。

(3)

式中:k为玻尔兹曼常数；T为绝对温度；B为接收机带宽；N为噪声因子；RL为负载电阻；ψi为探测器电流响应度。

则激光雷达噪声的等效概率密度描述函数可以表示为：

(4)

无噪声成像点云以及添加噪声成像点云结果如图6所示。

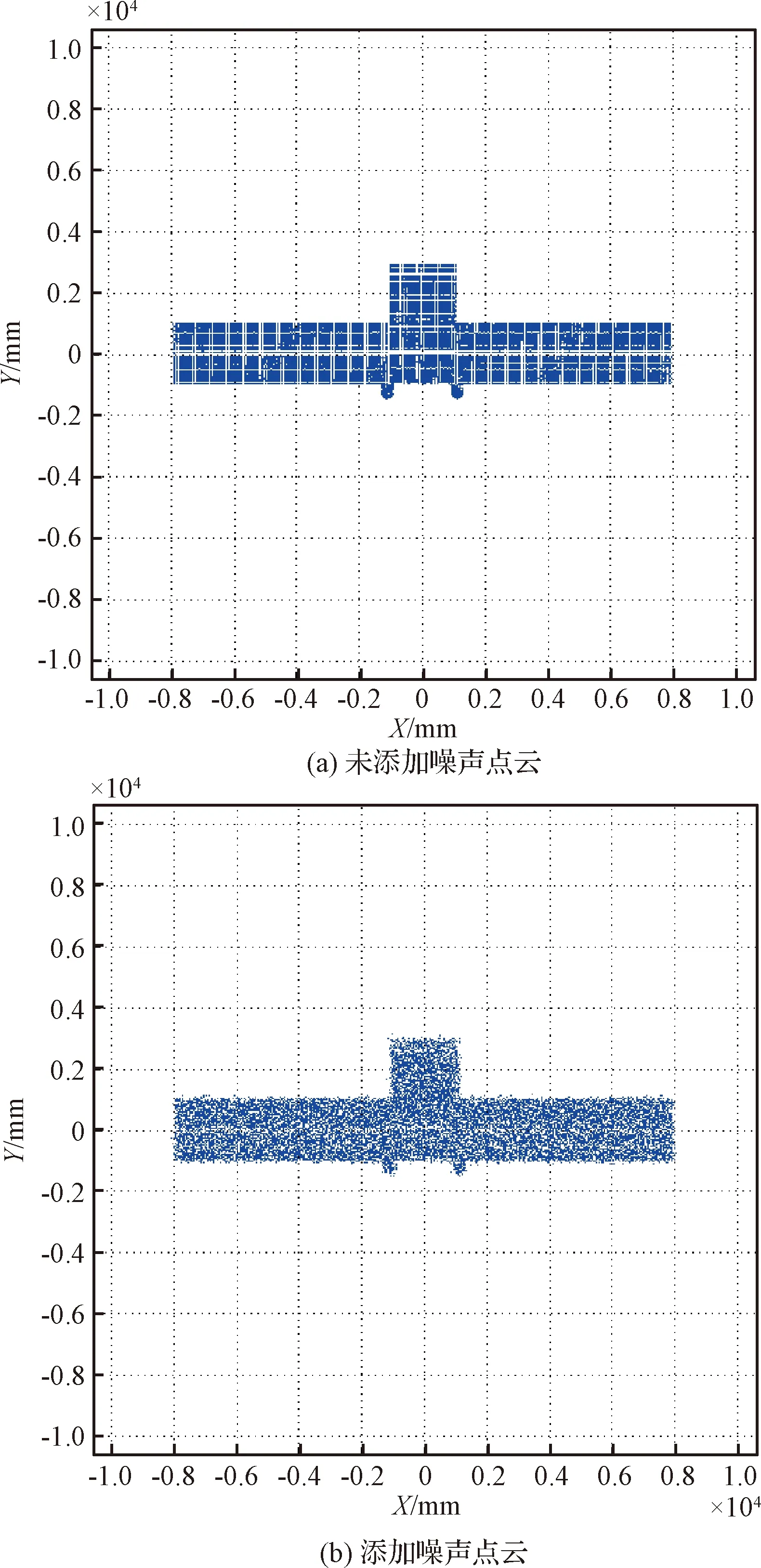
图6 点云噪声

在对点云添加相应的噪声后，根据雷达分辨率要求，对每一次线阵可视数据进行采样处理，使其满足实际雷达分辨率要求。

3 三维重建及质量评估

采用ICP算法对激光雷达扫描得到的不同视角扫描数据进行点云配准，根据配准结果进行点云三维重建[17]，并按照项目指标要求从对应点欧氏距离平均值、均方根值以及重建点云平均密度等方面进行重建质量评估。

3.1 点云配准

点云配准即将差分时间内扫描得到的点云数据按照相同的重合区域进行坐标变换，采用ICP算法进行位姿增量求解，获取其相对坐标转换关系：旋转矩阵R与平移矩阵T。在迭代过程中，根据一定的准则建立对应点集P与Q，对于点云P中的每个点pi，搜索其在点云Q上的最近点作为与之相对应的点qi，依据对应关系求解使得公式中目标函数达到最小的刚体变换，即旋转矩阵R和平移向量T，并将该变换作用于源点云，迭代进行这一过程直到满足某一设定的收敛准则。

(5)

式中:qi与pi分别代表两组扫描数据中各点的三维坐标。当配准结果相对于真实值三轴位姿精度小于1°时迭代终止。

3.2 逆序重建

根据ICP配准结果，按照式(6)对数据中的各点(x，y，z)依次进行逆向恢复重建。

(6)

三维重建从扫描数据的最后一帧开始恢复，直到第一帧数据恢复完成。具体流程如图7所示：(N组数据进行相邻帧配准共有N-1组配准结果)

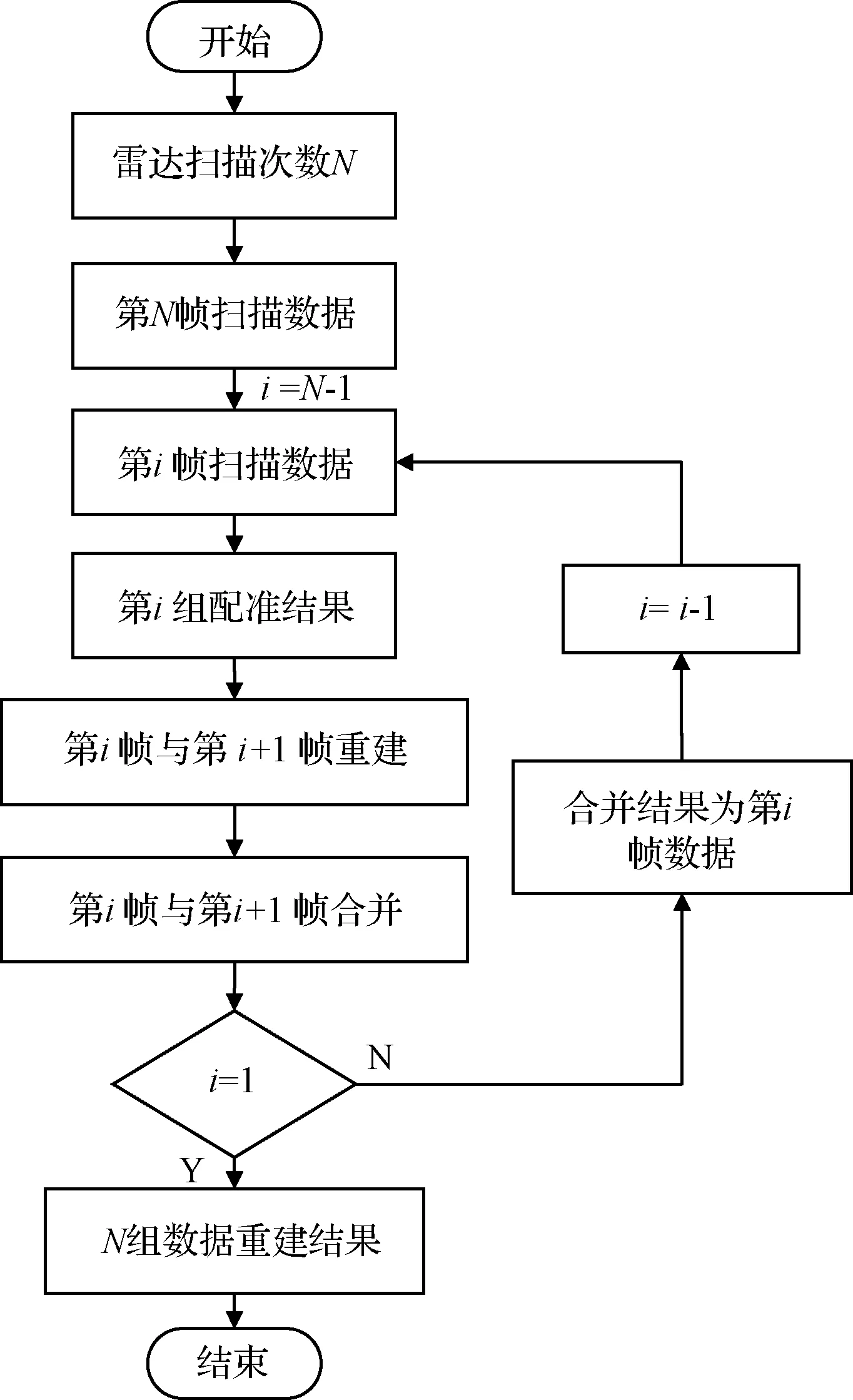
图7 逆序重建流程图

1)对i帧点云通过第i-1组旋转平移矩阵进行重建，得到恢复后的i′帧点云；

2)将重建后的i′点云与i-1帧点云进行合并，通过第i-2组旋转平移矩阵进行重建，得到恢复后的i-1′帧重建点云；

3)将恢复后的i-1′帧重建点云与i-2帧点云合并，通过第i-3组旋转平移矩阵进行重建，得到恢复后的i-2′帧重建点云；

4)同理，直到第2帧重建完成，将第1帧与其余帧重建结果点云合并，得到目标重建结果。

3.3 重建质量评估

1)点云精度

在目标原始点云数据生成时，对各点坐标添加相应的特征标记值，用于质量评估中的重建精度指标求取。

以点云中各点的标记值为配比信息，通过式(7)求取重建模型中的各点与原始CAD模型中的对应点(标记值相同)之间的欧氏距离dii′。

(7)

并对所有求取的对应点距离按照式(8)和式(9)进行距离平均值dave以及均方根值dRMS的计算，以进行重建点云精度进行评价。

(8)

(9)

2)点云平均密度

从重建模型主体表面截取一定长宽比的点云数据(1000 mm × 1000 mm)，采用二维面积逆向分析法求取点云平均密度。由于激光雷达扫描得到的数据是目标表面点云，因此忽略点云块中各点之间的Z坐标值之差，通过点云的X,Y坐标值即可进行面积求取。求取方式如下：假设点云是均匀分布的，则提取的点云面积可以通过点云的数量与点云之间的平均间距求得。如图8所示为平均分布的9×9的点云数据网格图(每两条线交点处为一个点)。

图8 面积法求取点云平均密度原理图

(10)

式中:Ncount为点云总数量，Dave为点云平均间距，Scloud为点云面积。

Scloud=(ymax-ymin)×(xmax-xmin)

(11)

因此可得，点云平均间距的计算公式为：

(12)

4 仿真实验及结果分析

4.1 目标模型建立

根据目标真实尺寸采用Creo软件进行目标三维模型的创建，并通过hyperworks点云转换软件将三维模型转换为点云数据。三维模型及点云模型如图9所示。

图9 目标三维模型及点云模型

4.2 实验环境建立

失稳运动目标参数：自旋速度5 (°)/s，章动速度5 (°)/s，章动角50°，章动轴方向为Y轴正方向，建立目标运动模型。

线阵激光雷达参数：成像分辨率为512×512(64线激光雷达，8次往复式扫描)，视场角20°，扫描帧率1 Hz。

三维重建指标要求：重建点云精度达到0.100 m(RMS)，重建点云平均密度达到0.03 m。

4.3 扫描成像实验

采用MATLAB软件进行仿真环境的建立，按照目标运动信息以及雷达成像机理，模拟进行激光雷达扫描成像，根据可见点判别方法完成对失稳目标进行多视角可测部位点云数据获取。其中部分扫描结果(第1帧，第55帧)如图10所示，左图为激光雷达视线方向。实验结果表示扫描成像数据输出率可达1 s/帧，且有效去除了被遮挡部位点云信息(文中算法结果均在CPU为Intel (R) Core (TM) i5-8500 CPU，3.00 GHz，内存为4 GB的PC机上运行所得，操作系统为Windows 10)。

图10 雷达成像仿真实验结果

文献[9]采用了一种基于准线的可视点云判别方法，逐列构造准线，根据运动点云与准线的位置关系确定可视点云。在工况环境相同的情况下进行了对比试验，得到的实验结果如图11所示。实验结果表示该方法在可视区域提取时会出现较多的误点，提取的点云不均匀，并且实验耗时为24 s/帧，远高于1 s/帧，难以满足实际工况验证要求。

4.4 三维重建实验

采用ICP算法对相邻帧扫描点云进行配准，求取两次扫描间隔时间内目标位姿增量信息，分别为沿三轴平移与绕三轴旋转信息，其结果如图12所示。

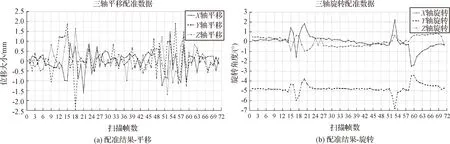
图12 点云配准结果

从图11可以看出，在激光雷达对空间失稳目标扫描过程中会出现两次目标特征突变，导致特征突变处的点云配准结果误差较大，配准结果不理想，因此通过对误差较大点的去除以及数据的拟合，对配准结果进行修正。以配准结果和多帧扫描数据为先验信息，根据逆序重建流程进行目标三维重建。重建的结果如图13所示。

4.5 数据冗余分析及改进

通过图13重建结果可以看出，若采用全部扫描结果进行配准及重建，由于配准结果误差，导致在逆序重建时会出现误差累积，随着数据量的增加误差累积效果越明显。因此按照项目提出的指标要求，提出在满足目标重建点云平均密度要求的情况下，对参与重建的点云数据进行采样筛选处理，即对间隔一定帧数的扫描数据进行实验，避免使用特征突变处的扫描结果，提高三维重建精度。根据扫描数据量大小以及工况环境共进行5组(间隔的帧数分别为：3帧、4帧、5帧、6帧、8帧)采样重建实验，其结果如表1所示。

表1 数据采样处理后重建精度分析结果

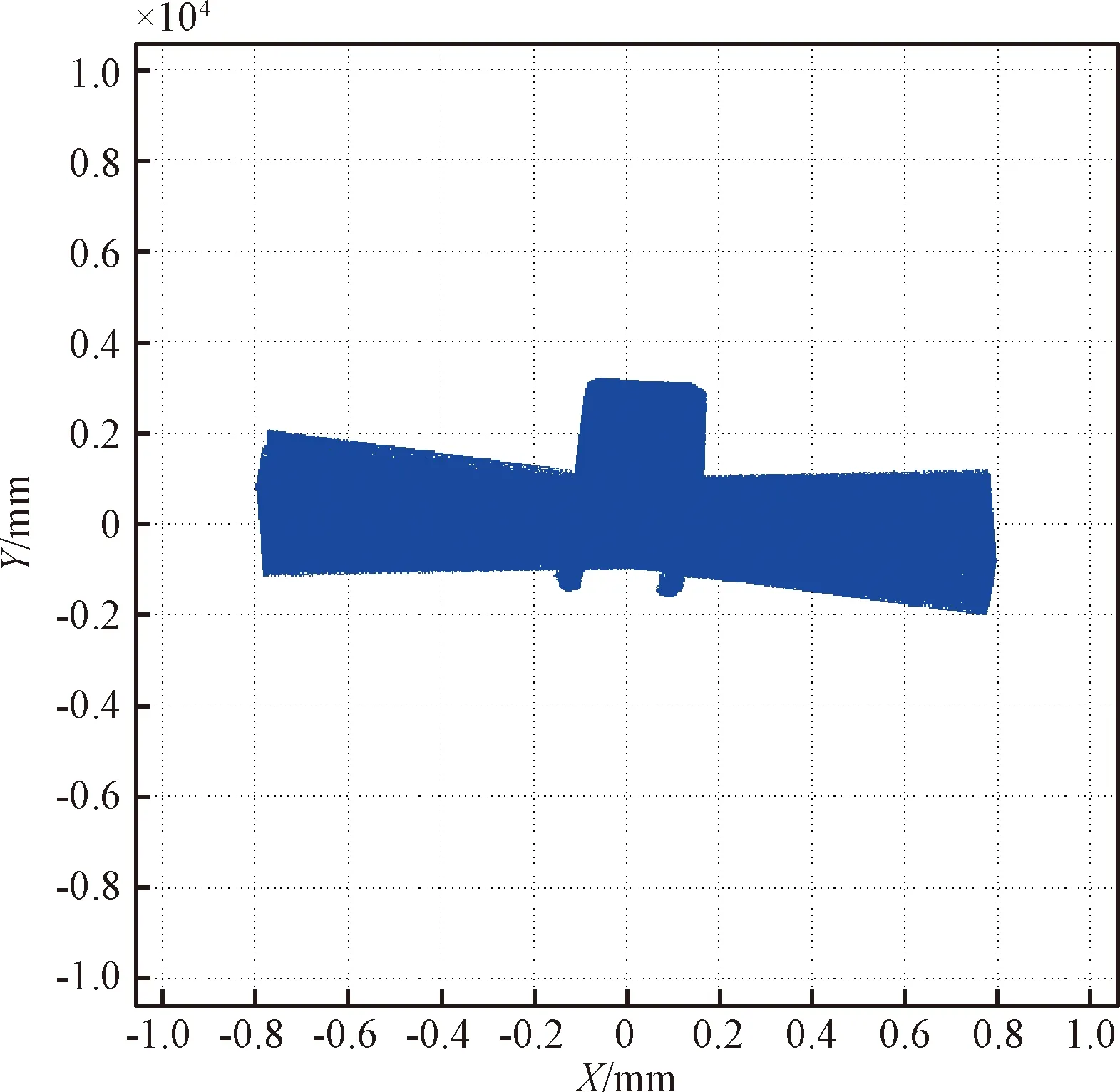
图13 三维重建实验结果

按照某型号地面处理任务要求，由于实际任务中的数据传输带宽限制，所需的重建点云平均密度并不是越大越好，点云密度要求的增大会带来点云数据量以及运算量的增大；并且不同性质、类型、尺寸的目标在点云平均密度上的要求是不同的，综合项目提出的点云重建精度与平均点云密度指标要求，选取最优点云处理方案。

对照项目指标要求，经过数据冗余分析、采样配准重建实验，得出在以5帧为采样间隔的实验结果中达到了最值，重建效果最佳，并且满足任务指标要求。因此以5帧为间隔进行配准、重建时，可有效避开不同帧扫描数据中特征变化较大点，降低累积误差，提高重建点云精度。

5 结 论

本文针对空间失稳目标动态测量及三维重建问题，提出一种基于双切片法的可见点提取机制，有效提取目标多视角下可测点云信息；同时以ICP配准结果为先验信息进行逆序重建，分析数据冗余情况，降低累积误差，建立三维重建质量评价指标，按照项目指标要求闭环控制点云重建筛选方案及重建精度，实现最佳重建方案。针对本文的目标模型以及工况环境，得出在以5帧为采样间隔的情况下，得到的重建结果最佳(重建精度：90.25 mm<100 mm，点云密度19.93 mm<30 mm)。该方法可为地面验证及在轨应用提供数据及理论支持。由于不同扫描环境下带来的数据冗余情况不同，未来将进一步探索最优帧数间隔对不同目标重建质量的影响规律。