在轨服务中的仿生抗冲击结构研究
王 鑫,岳晓奎,代洪华,袁建平
(1. 西北工业大学航天学院,西安 710072;2. 西北工业大学航天飞行动力学技术国家级重点实验室,西安 710072)
0 引 言
随着人类航天事业快速发展,在轨服务[1-4]成为一种新趋势,引起了人们的广泛关注。其中,在轨抓捕扮演着非常重要的角色。而服务航天器在抓捕空间目标时,特别是对于非合作目标来说,由于缺少全部或者部分状态信息,执行器末端和目标之间存在着相对速度,使得两者必然发生碰撞,进而产生不期望的振动[5],而这些振动在低阻尼的空间微重力环境下往往会持续很长一段时间[6],这会对安装在航天器主平台的精密仪器的正常工作产生严重的影响。如何快速有效地消除这些振动,对于确保组合航天器的安全和稳定至关重要。
一般来说,被动隔振具有可靠性高、易于实施、成本低等优点[7-8],因而被广泛应用在工程实践中。近几年来,被动式非线性隔振系统引起了学者们的极大兴趣。其中香港理工大学景兴建教授团队[9-12]受自然界中高速奔跑的袋鼠腿部结构的启发,提出了一种仿生X形结构,此结构具有良好的非线性刚度和阻尼特性。它能够克服一些传统的弹簧质量阻尼器、准零刚度阻尼器和主动隔振的不足,并且可以通过调节X形结构的层数、连杆长度、安装角等结构参数来实现被动调节结构的非线性刚度和阻尼特性。此外,通过在结构内部嵌入仿生X形结构来模拟人在行走时腿部肌肉和肌腱的功能,取得了良好的隔振效果[13]。在此基础上,文献[14-16]将仿生X形结构安装在航天器机械臂和抓捕机构之间来降低服务航天器在执行空间目标抓捕任务时由于执行器末端和目标之间的碰撞对航天器主平台的影响,并通过建模分析,仿真校验其在受到外冲击力和周期激励下具有良好的振动隔离效果。
基于此,本文将嵌套仿生X形结构替代单层仿生X形结构安装在航天器机械臂和抓捕机构之间,如图1所示,并通过建模分析此嵌套仿生X形结构隔振系统在受到外冲击力情况下的抑振性能。
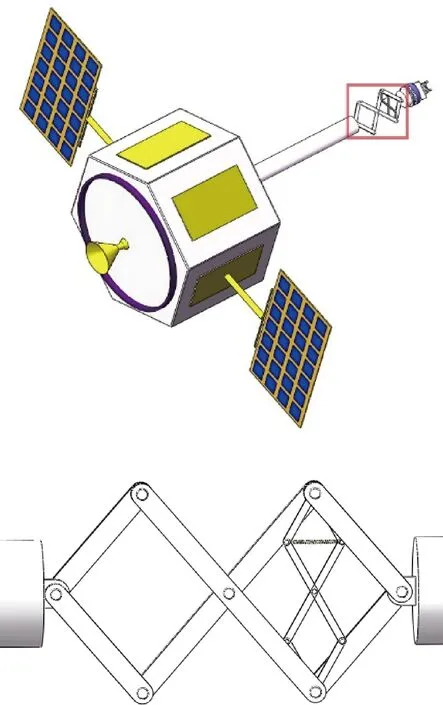
图1 在轨抓捕任务示意图
1 动力学模型的建立
1.1 几何关系


图2 嵌套仿生X形结构隔振系统示意图
嵌套仿生X形结构单元初始和形变后状态的几何关系如图3所示,其中实线和虚线分别表示初始和形变后状态,其中φ,θ分别表示内外层仿生X形结构支撑杆的旋转角。为了更清晰地得到内外层X形结构的运动关系,内外两层X形结构形变前后状态分别在图4 (a)和图4(b)中展示。

图3 嵌套仿生X形结构初始和形变后的几何关系

图4 内外层X形结构的位移
根据图4中所示运动关系,可以得到

其中,φ和θ分别表示内外层仿生X形结构的关节旋转角。x为内层X形结构的横向压缩长度,x′为外层X形结构的纵向伸展长度。由此可以得出
1.2 拉格朗日方程
利用拉格朗日方程来建立系统的动力学方程。
嵌套仿生X形结构系统的动能可表示为
(1)
其中,支撑杆和关节的质量远远小于m1和m2,忽略不计。
系统的势能主要是弹簧的弹性势能,表示为
(2)
式中:k为弹簧刚度系数,x为弹簧水平变化长度。
系统中非保守力所做的虚功可表示为

由式(1)和式(2)可得拉格朗日函数为
(3)
由拉格朗日方程可以得到
(4)
式中:
那么系统的动力学方程为

(5)

(6)
为方便起见,定义式(5)和式(6)中的四个非线性函数f1,f2,f3,f4如下所示:
那么系统动力学方程简化为
(7)
(8)
式中:
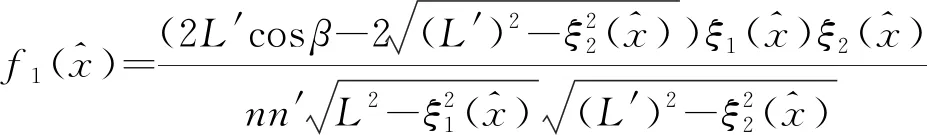
其中,


(9)
其中,系数aij(i=1,…,4;j=0,…,3)的具体表达式如下所示:
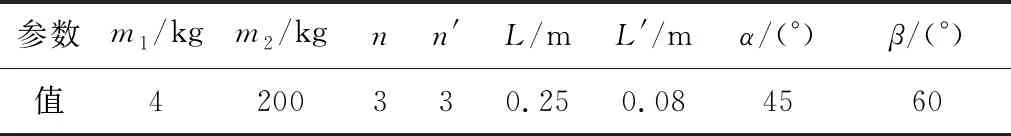
表1 结构参数设置

图5 原始函数和近似泰勒级数展开比较
(10)
(11)
2 冲击力下的拉格朗日方程
当航天器执行在轨服务任务时,目标会对执行器末端施加一冲击力,在这种情况下,需要对原有的拉格朗日方程进行改进。此时的拉格朗日方程为
(12)

(13)

(14)
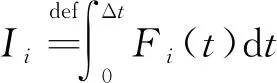
3 隔振性能分析
在轨服务中,能否成功捕获目标至关重要。由于服务航天器和目标之间相对速度的存在,使得抓捕机构末端和目标碰撞在所难免。本部分主要分析系统在受到外冲击力下的响应,根据前面分析,将外冲击力Fi(t)对系统的影响看作是对抓捕机构末端施加一冲量Ii。结构参数设置如下:
m1=4 kg,m2=200 kg,cr=0.15 Ns/m
c1=0.2 Ns/m,c2=0.2 Ns/m,L=0.25 m
k=1000 N/m,n=2,n′=2,α=π/4
β=π/3,I=0.8 kg·m/s
3.1 隔振性能
系统在受到外冲击力作用下,m1和m2的位移、速度随时间变化的曲线如图6(a)和图6(b)所示。从图6(a)可以看出,m1和m2沿着一条斜线上下摆动,由此可以推测出它们的运动不仅包括振动,还包括平动。此外,m1和m2最终趋于一条直线,说明振动部分会随着时间被耗散掉。从图6(b)可以看出,在外冲击力的作用下,m1的初速度为0.2 m/s。m2的速度远远小于m1,并且m1和m2最终以3.9 mm/s的速度飘移。为了更好地分析系统的振动响应,将飘移去掉,只研究m1和m2的轴向运动。图7展示了系统在去掉飘移后m1和m2的位移、速度和加速度随时间的变化图。从图7(a)~图7(b)可以看出,系统在大约3 s之后振动完全消失,m1和m2的最大位移分别是1.8×10-2m和3.6×10-4m,最大速度分别为0.2 m/s和5.7×10-3m/s,m1的最大速度发生在t=0时刻。而加速度作为最重要的评估指标如图7(c)所示,m1和m2最大加速度分别为1.1 m/s2和0.02 m/s2,加速度显著减小。由此可见,由外冲击力所产生的振动在经过嵌套仿生X形结构隔振系统作用以后,m2所表示的航天器主平台振动幅值大大降低。

图6 在受到冲量I=0.8 kg·m/s下,m1和m2位移、速度随时间变化曲线图

图7 在受到冲量I=0.8 kg·m/s下,m1和m2的位移、速度和加速度随时间变化关系图(去掉飘移后)
3.2 与单层仿生X形结构和弹簧质量阻尼器比较
本节将嵌套仿生X形结构与单层X形结构以及传统弹簧质量阻尼器的隔振性能进行比较。将三者的弹簧刚度设置为k=1000 N/m,其他参数设置保持不变。系统在受到外冲击力的作用下,m1和m2的位移、速度和加速度如图8所示。图8 (a)和图8(b)展示的是三者的位移变化曲线。从图8(a)和图8(b)可以看出,嵌套仿生X形结构和单层X形结构系统在大约3 s和12 s时趋于稳定,而弹簧质量阻尼系统一直处于上下震荡状态且降幅缓慢,这说明仿生X形结构优良的非线性刚度和阻尼特性。尽管在初期相较于弹簧质量阻尼系统会有一较大的瞬时抖动,但很快系统会稳定下来。从m1和m2的速度随时间变化的曲线图8(c)和图8(d)可以看出,经过嵌套仿生X形结构隔振系统后,不论是m1还是m2,与弹簧质量阻尼系统和单层X形结构相比,速度下降更快,系统能够在更短的时间内稳定下来。加速度作为最重要的预估系统隔振效果的指标,因为作用在航天器主平台上的惯性力一般与加速度成正比,这里的m1和m2加速度曲线在图8(e)和图8(f)中展示。从图8可以看出,经过嵌套仿生X形结构系统隔振后,m1和m2的加速度远小于其他两种隔振系统,隔振效果更好。嵌套仿生X型结构和单层仿生X形结构相比,不论从位移、速度还是加速度,前者明显优于后者,这说明内嵌套X形结构提升了外层X形结构的隔振性能,因为内嵌套X形结构的存在提高了系统的非线性刚度和阻尼特性。
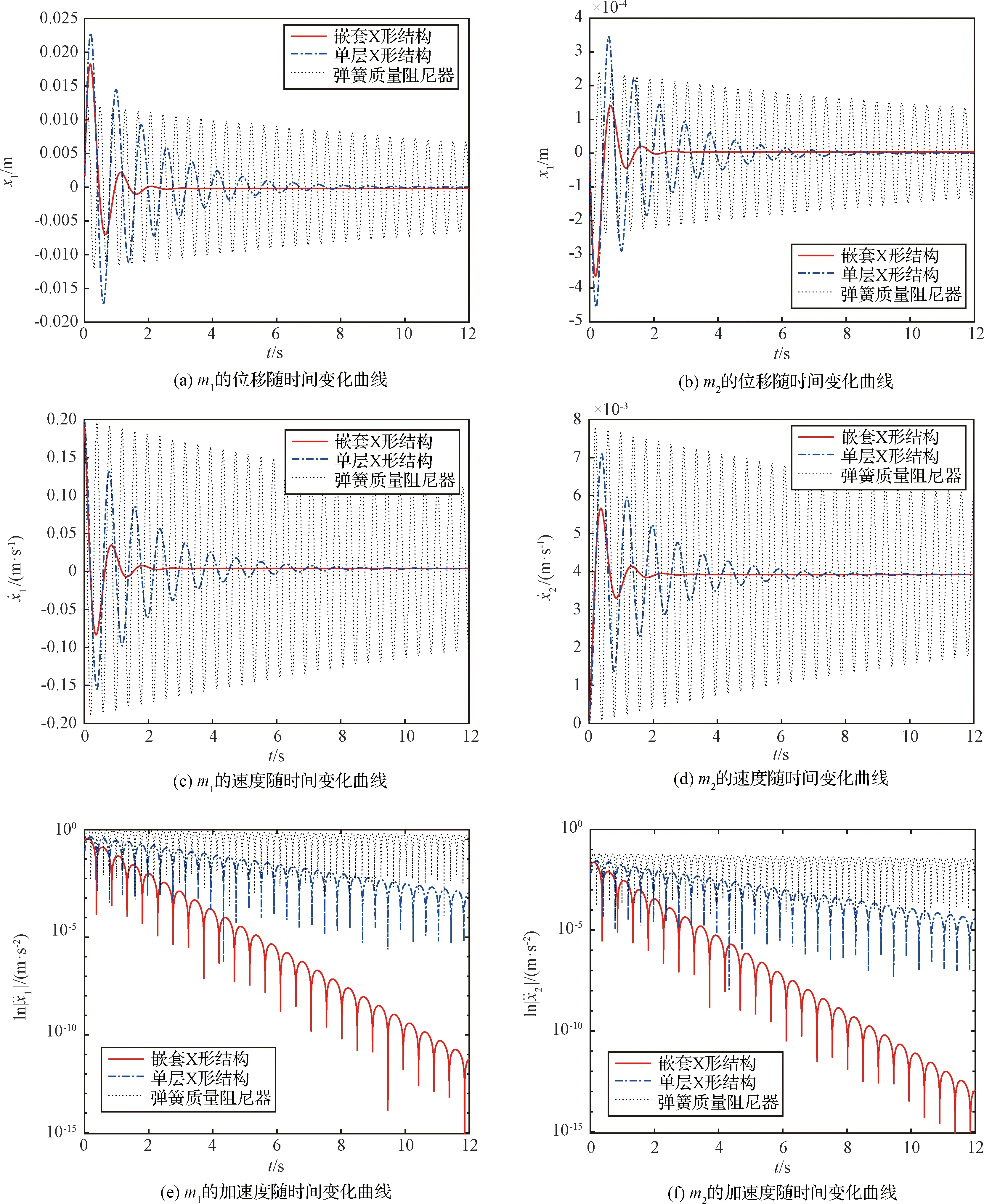
图8 三种不同隔振系统下m1和m2的位移、速度和加速度随时间变化曲线
4 结 论
当服务航天器执行在轨服务任务时,由于末端执行器与目标的速度不匹配,导致两者之间必然发生碰撞,进而产生不期望的振动,而这些振动在低阻尼的太空环境下往往会持续很长时间,这对航天器主平台的正常工作产生严重的影响。本文提出将嵌套仿生X形结构安装在航天器机械臂与抓捕机构中间来抑制由目标与执行器末端碰撞而产生的振动,对此隔振系统进行建模分析,并与传统的弹簧质量阻尼器和单层仿生X形结构隔振系统进行比较,仿真校验表明,嵌套仿生X形结构系统具有更好的隔振性能,能够更加快速而有效地抑制航天器的抓捕后振动。

