吸气式组合动力高超声速飞行器上升段制导方法研究

刘 凯，郭 健，周文雅, 佘智勇

(1. 大连理工大学航空航天学院，大连 116024；2.辽宁省空天飞行器前沿技术重点实验室, 大连 116024；3.北京空天技术研究所, 北京 100074)

0 引 言

吸气式高超声速飞行器[1-5]是指飞行马赫数大于5，采用吸气式及其组合动力，能够在距海平面20～100 km高度进行机动飞行，可执行打击、侦查、运载与对抗等任务的飞行器。高超声速飞行器具有快速响应、突防能力强、自由廉价进入空间等技术特点，具有巨大的军事意义和政治意义。作为导弹武器使用，可实现全球快速打击，利用速度和空域优势对抗敌方防空反导体系；作为高超声速飞机使用，可对高威胁区域进行快速抵近侦察，提供基于信息系统的体系作战能力；作为空天往返飞行器使用，具有可重复使用、水平起降和拓展发射窗口等特点，可大幅降低发射成本、增强飞行可靠性，并具备执行战时应急入轨能力。

美国通过X43A、HyFly及X51A等演示验证飞行器计划的推进，已经在高超声速巡航飞行技术方面积累了深厚基础，目前以洛克希德马丁公司和波音公司为代表已经开启了以吸气式组合发动机为动力、适应大空域宽速域飞行任务的高超声速飞机的研究中。国内外学者对组合动力高超声速飞行器爬升段飞行轨迹设计进行了一些研究工作。文献[6]在进行爬升段轨迹设计时，考虑了加速度设计对于燃料消耗的影响，将最大加速度爬升方案所得轨迹与燃料最省爬升轨迹进行对比，并且提出了航迹倾角变化率的约束条件。在轨迹优化方面，文献[7]研究了单级入轨的高超声速飞行器上升段轨迹，结合群体智能随机优化算法和确定性梯度算法，考虑飞行过程中的动压约束，最大有效载荷为优化性能指标，最终获得最优上升段轨迹。文献[8]则以两级入轨飞行器为研究对象，通过定义飞行器自身结构与燃料质量之间的等式关系，然后通过优化飞行轨迹得到燃料最省轨迹来达到减小既定油箱容积的目的。

然而，多数文献在研究中直接应用目前成熟的直接法、间接法以及智能优化算法等，从数学上获得能量最优或爬升时间最短的飞行轨迹，但从不同飞行阶段的升重/推阻匹配等物理机理出发，来研究飞行策略从而进行轨迹设计的工作并不多。

在轨迹跟踪制导方面，文献[9]针对一类具有非最小相位特性的吸气式高超声速飞行器，给出了判定非线性系统为非最小相位系统的判据，并利用动态逆方法完成了纵向轨迹跟踪控制设计。针对高超声速飞行器纵向模型的快时变、强耦合和高度非线性的特点，文献[10]针对吸气式高超声速飞行器，在考虑模型不确定性的情况下，采用李导数的方法对某型高超声速飞行器进行输入输出的精确线性化，并基于线性化后的模型提出一种非线性动态逆控制方法,实现对该型高超声速飞行器的轨迹跟踪控制。文献[11]针对滑翔式高超声速飞行器建模不确定性强的特点，使用具有较强鲁棒性的ADSC方法实现鲁棒路径跟踪，仿真结果表明该制导方法可以有效处理具有模型不确定性条件下的再入轨迹跟踪制导问题；文献[12]针对多约束条件下高超声速飞行器再入制导问题，提出一种基于微分变换法求解最优反馈控制的全状态标准轨迹跟踪制导律，通过最优控制理论将制导指令解算问题转化为两点边值问题，采用微分变换法进行求解获得最优反馈控制律。

当前多数高超轨迹跟踪制导问题的研究集中在吸气式巡航段以及无动力滑翔段，对于组合动力爬升段制导问题的研究成果较少；同时，由于组合动力爬升段经历不同推进模态，推力特性受飞行姿态角及火箭流量的影响迥异，给轨迹跟踪制导问题带来新的难点。

基于此，本文针对涡轮/冲压/火箭三组合动力水平起降高超声速飞行器为研究对象，分别分析了涡轮段、引射段、冲压段及冲压火箭段的飞行策略，给出了适合的攻角剖面构型，进而结合直接法中的序列二次规划算法，完成了组合动力高超声速飞行器上升段飞行轨迹设计工作；在此基础上，结合轨迹线性化控制方法[13-15]，开展了组合动力上升段轨迹跟踪制导律设计研究，给出了保证闭环稳定性和控制品质的制导律参数设计准则，最后通过对标称情况和拉偏情况的仿真证明了方法的有效性。

1 组合动力爬升段轨迹设计与制导模型

1.1 质点动力学模型

本文忽略地球自转影响，根据弹道坐标系与地面坐标系之间的转换关系，可建立涡轮/冲压/火箭三组合动力高超声速飞行器纵向质点动力学方程为：

(1)

式中:h,V,θ,m,R分别表示飞行高度、速度、弹道倾角、质量、航程，T,D,L分别表示发动机推力、阻力、升力，Isp表示比冲，α表示攻角，re为地球半径。考虑高超声速飞行器采用涡轮、冲压和火箭三组合动力[16]，其中发动机推力特性依赖于飞行马赫数、动压及攻角和火箭流量等，且不同模态下影响关系和影响特性不同，可以描述为如下分段形式

(2)

式中:Ma表示飞行马赫数,q表示飞行动压,kr表示火箭流量大小。

1.2 轨迹优化问题描述

爬升段轨迹设计约束主要包括动压、热流、过载、攻角幅值等约束条件，可以描述为如下形式：

(3)

另外，飞行器轨迹需要满足终端约束，即

(4)

选用燃料最省作为性能指标，则飞行轨迹设计问题可以转化为如下最优控制问题：

(5)

1.3 轨迹跟踪制导问题

轨迹跟踪制导问题可以描述为：对于给定的爬升段标称轨迹

(6)

设计合适的制导规律

[α(t),kr(t)]t∈[t0,tf]=[K1(e(t)),

K2(e(t))]t∈[t0,tf]

(7)

使得组合动力爬升段实际飞行状态较好的跟踪标称飞行轨迹中装订的飞行状态，这里

(8)

表示飞行过程中实际状态与标称状态之间的偏差。

2 飞行轨迹设计

2.1 飞行策略

下面分阶段给出飞行策略。

1)涡轮段飞行策略

如果从起飞爬升至安全高度后开始考虑，则在亚声速阶段应当将弹道拉起，以避免高动压飞行，保证在跨声速阶段不会有过多的阻力损失，跨声速结束后再通过降低爬升率避免出现过低动压情况，利于涡轮发动机加速爬升。

2)引射火箭段飞行策略

由于此阶段主要依靠火箭动力加速，因此先采用火箭动力高弹道策略，将弹道拉起减小阻力消耗，由火箭动力快加速，然后为了满足后续纯冲压段高动压的需求，降低爬升率增加动压，保证在引射火箭段结束时的动压达到纯冲压理想工作状态。

3)纯冲压段飞行策略

此时单纯冲压通道产生的推力已经足够克服飞行器所受阻力，同时发动机处于亚燃状态比冲较高，为了发挥高比冲优势，采用维持等高动压飞行策略。

4)冲压火箭段飞行策略

采用BANGBANG控制形式，即在某个马赫数之前为纯冲压工作状态，过了这一阀值后则切换到火箭流量开到最大的状态。这一阀值马赫数可以作为设计变量优化得到。待进入冲压火箭共同加速飞行段，同样主要采用火箭飞行策略将弹道拉起，降低阻力消耗，然后将弹道拉平，满足终端高度、速度及弹道倾角需求。

2.2 攻角剖面形式

第2.1节分析了不同飞行阶段采用的飞行策略，对应上述飞行策略，各阶段采用如下的攻角剖面形式。

1)涡轮段

攻角剖面采用以马赫数为调度变量的多项式形式，且应为前一段为较大攻角，随着马赫数增加攻角减小至零度附近，跨声速加速后再适当提升攻角，避免高度过低，不利于引射火箭段工作。

2)引射火箭段

攻角剖面仍然采用以马赫数为调度变量的多项式形式，且前一段为大攻角，拉升弹道，后将攻角减小至负数，压低弹道满足终端理想动压需求。

3)纯冲压段

火箭流量为关闭状态，所有控制量仅有攻角一项，为保证等动压飞行实际上攻角是唯一确定的，可采用牛顿迭代计算得到攻角指令。

4)冲压火箭段

火箭流量为开满状态，控制量只有攻角，仍然可采用以马赫数为调度变量的多项式形式。

2.3 参数优化求解

将上述攻角剖面构型代入原优化问题后，可将无穷维轨迹优化问题转化为有限维非线性参数规划问题，非线性规划问题一般形式可表示为：

(9)

其中，目标函数f和ci均为定义于Rn中的二阶连续可微函数。设x*为上述问题的局部最优解。若在x*处起作用约束条件，即有ci(x*)=0成立的约束条件的梯度向量▽ci(x*)线性无关，则存在满足下列Kuhn-Tucker条件的向量组(x,λ)=(x*,λ*)

(10)

(11)

其中,λ=[λ1,λ2,…,λm]T是拉格朗日乘子向量。上述最优性条件可由序列二次规划(SQP)算法[7]求解，图1为求解流程图。

图1 SQP算法流程图

3 轨迹跟踪制导

3.1 轨迹线性化

针对高度和速度剖面跟踪需求，将高度/速度项影响作为关注状态变量，引入速度积分项、高度微分项对状态方程扩维，增广轨迹动力学模型如下：

(12)

描述为状态空间形式为

(13)

(14)

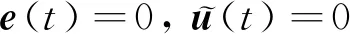
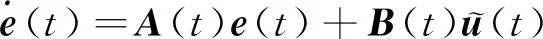
(15)

式中:

假设1. 为了应用基于期望极点配置的轨迹线性化控制方法，本文假设控制输入矩阵非奇异，即满足

3.2 跟踪制导律设计

针对线性化后的时变系统，采用如下形式的时变控制器，包括标称轨迹设计中的前馈控制部分以及误差时变反馈控制器

(16)

其中,

将控制器代入误差时变系统，并设期望闭环系统的系统矩阵为

(17)

令代入闭环控制器的误差时变系统的系统矩阵与期望系统矩阵相等，可解出控制器参数

徐州传统地方戏曲梆子戏在2008年被列为国家级非物质文化遗产，江苏梆子剧院有限公司（前身江苏省梆子剧团），现已实行企业化管理。梆子戏在徐州、河北地区目前仍继续上演，有一批固定观众。

3.3 期望系统矩阵设计

从第3.2节可以看出，控制参数由期望特征根决定，所以核心问题在于期望特征根的选取。从期望闭环系统矩阵可以看出，两个子空间均可描述为线性时变的二阶系统，描述为特征方程形式即为

(18)

因此有

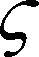
按照目前欠阻尼二阶线性系统对于阶跃响应的上升时间和超调量估算公式：

(19)

(20)

则给定需求的闭环控制系统上升时间和超调量联立求解出期望系统的阻尼比和频率，进而确定期望系统矩阵特征根，获得控制器参数。

3.4 稳定性判据

第3.3节给出了控制结构和控制参数设计方法，本节给出轨迹线性化时变控制器稳定性分析判据。

引理1[17].对于闭环误差线性时变系统(15)，若系统PD特征值

(21)

满足

1)存在常数c1,c2满足

(22)

2)存在正整数m满足

(23)

那么时变闭环系统是一致稳定的。

利用上述定理分析时变线性控制器，由于轨迹线性化控制器加入后的闭环系统PD特征值为

那么，只要存在正常数c保证

ωn(t)>c>0,t>0

则显然式(21)～式(22)均成立，基于上述PD特征根设计出的控制器可以保证闭环时变系统稳定，因此上述引理提供了选取期望闭环极点的准则，以便支撑轨迹线性化控制参数设计工作。

4 仿真校验

4.1 组合动力爬升飞行轨迹仿真

本节以面向水平起降高超声速飞行任务需求的涡轮/冲压/火箭组合动力飞行器方案[18]为仿真对象，考虑起飞至安全高度后，开展爬升段飞行轨迹设计研究，考虑终端飞行速度Ma6，高度为26 km，飞行攻角不超过15°，涡轮段工作Ma上限为1.5，纯冲压工作起始状态为Ma3，冲压火箭段起始工作状态为Ma5，应用本文提出的基于飞行策略分析的分段轨迹设计方法，可完成组合动力爬升段轨迹设计。

从图2～图7可以看出，利用本文提出的爬升段轨迹设计方法，可以满足飞行过程约束(飞行动压及攻角并未超限)，并较好地满足了终端状态约束(终端飞行高度和马赫数)。

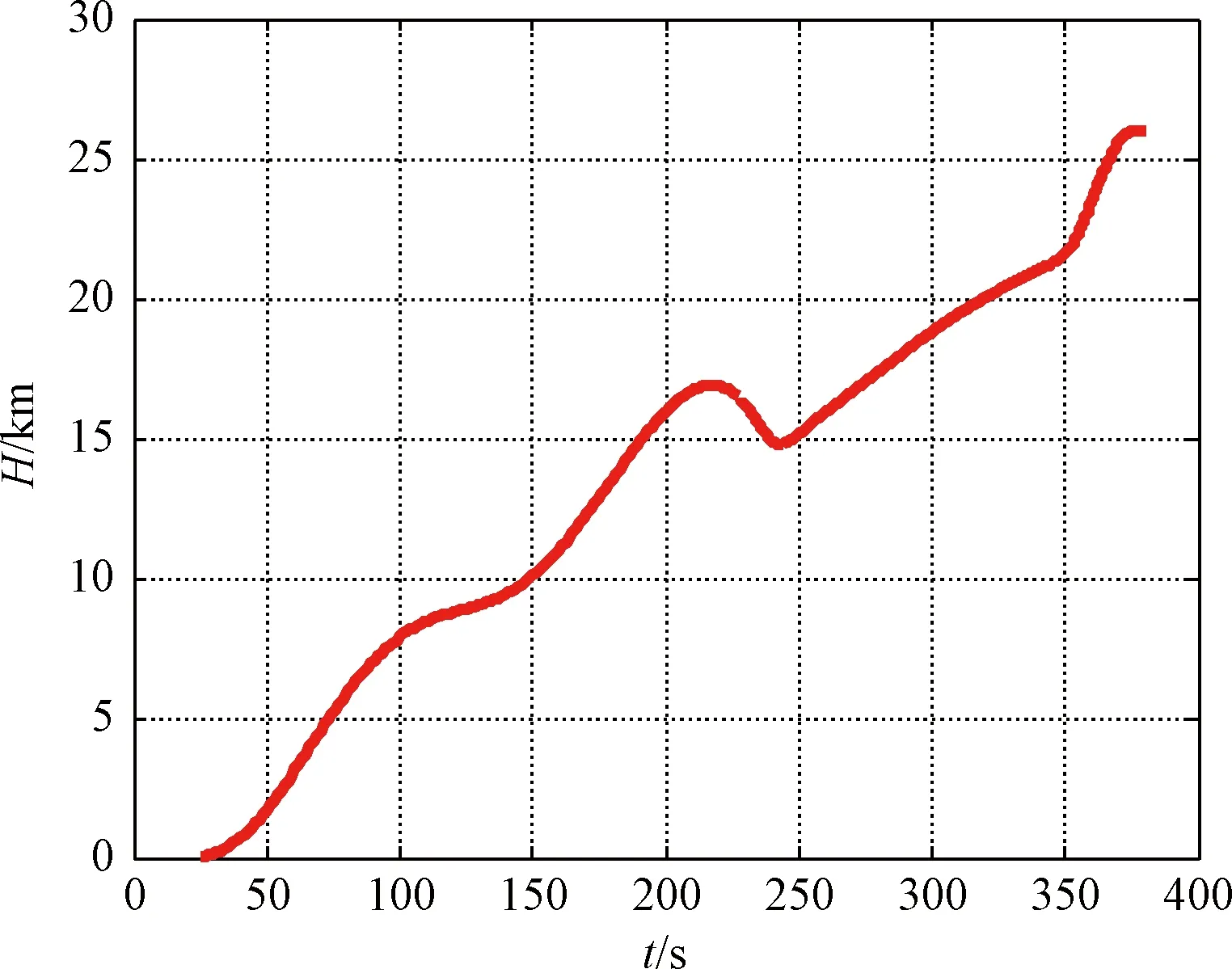
图2 高度随时间变化曲线

图3 速度随时间变化曲线

图4 质量随时间变化曲线

图5 马赫数随时间变化曲线

图6 飞行动压随时间变化曲线

图7 攻角随时间变化曲线

4.2 组合动力爬升轨迹跟踪制导仿真

针对设计获得的标称飞行轨迹，利用本文提出的基于轨迹线性化控制的制导方法，开展了跟踪制导律设计，并在考虑气动性能拉偏的条件下，开展了仿真分析。为分析升阻系数向不同方向变化条件下的制导性能，分别将涡轮段升力系数向下拉偏20%、引射段阻力系数向下拉偏20%、纯冲压段阻力系数向上20%、升力系数向上20%，获得仿真结果如图8～12所示。

图8 高度跟踪结果随马赫数变化曲线

图9 速度跟踪结果随马赫数变化曲线

图11 火箭流量随马赫数变化曲线

图12 质量随马赫数变化曲线

从图8～9可以看出，即使在升阻系数20%拉偏条件下，组合动力爬升段中各阶段制导律都能较好地保证实际飞行状态较好地跟踪标称飞行轨迹，证明了方法的有效性。此外，从图10～12可以看出，为了消除升阻系数拉偏带来的跟踪误差，实际攻角指令和火箭流量指令在标称指令的基础上进行了自主调节，因此燃料质量较标称轨迹燃料消耗有一定差别。

图10 攻角随马赫数变化曲线

4.3 对比仿真分析

考虑到涡轮冲压火箭三组合动力高超声速飞行器上升制导方法目前研究较少，为了比较本文提出基于轨迹线性化控制制导方法，在相同设计条件下开展了基于PID控制的轨迹跟踪制导设计及仿真分析，为了较好地看出跟踪效果对比截图，截取了第一段跟踪误差对比图。

从图13～图14可以看出，基于轨迹线性化控制制导途径对应速度跟踪误差明显小于PID控制途径，高度剖面跟踪误差方面也是轨迹线性化控制途径在大部分阶段和最终状态小于PID控制途径，这些都说明了提出基于轨迹线性化控制制导方法应用于吸气式组合动力高超声速飞行器上升段制导问题的优势。

图13 高度跟踪误差对比结果

图14 速度跟踪误差对比结果

5 结 论

本文综合考虑组合动力高超声速飞行器爬升段不同阶段的动力特性和气动特性差异，从物理规律入手提出了不同发动机工作模态下的飞行策略，在此基础上通过给出适合的攻角和火箭流量剖面构型形式，将飞行轨迹设计问题转化为有限维参数规划问题，完成了组合动力上升段飞行轨迹的优化设计。同时，采用轨迹线性化控制方法，给出了跟踪制导律结构、参数设计准则以及稳定性分析判据，发展了组合动力上升段轨迹设计和跟踪制导律设计手段，为以水平起降高超声速飞机为代表的下一代高超声速飞行器制导方案提供了潜在的技术途径。