空间机器人动力学奇异回避的笛卡尔轨迹规划
金荣玉,耿云海
(哈尔滨工业大学卫星技术研究所,哈尔滨 150001)
0 引 言
空间机器人可以代替人类在恶劣的太空环境中工作,降低成本,提高空间探索的效益。因此,世界各大国家都加大力度发展空间机器人在轨服务技术,如美国的Orbital Express项目[1]、中国天宫二号机械臂。而自由漂浮空间机械臂不仅可以节省燃料,还可以避免捕获过程中基座过控制产生的机械臂末端与目标的碰撞。因此,一直以来,自由漂浮空间机械臂是学者们研究的重点。本文主要研究自由漂浮空间机械臂的轨迹规划。
空间机器人笛卡尔空间轨迹规划不可避免地会遇到动力学奇异的情况,造成轨迹规划失效[2]。针对动力学奇异,研究者们已经取得了很多成果。很多研究者在轨迹规划中,只运用正运动学方程,故不存在动力学奇异问题[3-8]。然而,此类方法不适用于笛卡尔空间任务[9]。Papadopoulos以2个关节的平面机器人为例,提出了一种基于机械臂的工作空间的动力学奇异回避方法[10]。但是,对于多自由度的空间机器人而言,其工作空间的计算要更为复杂,加大了轨迹规划的难度。Nanos等通过求解合适的空间机械臂关节角及基座姿态的初始值,使设定的轨迹不会遇到广义雅可比矩阵奇异的情况[9,11]。然而,该方法忽略了基座姿态扰动。一般情况下,阻尼最小方差法也可用于空间机械臂动力学奇异回避问题,但是仍然会牺牲机械臂末端在各个方向的位姿精度[12-13]。顾晓勤等[14]也对空间机器人的动力学奇异特性进行了分析,并采用反馈控制的方法减小动力学奇异导致的轨迹的偏离。因此,目前急需一种适用于高自由度空间机械臂笛卡尔路径规划的动力学奇异回避方法。
由于某些空间任务(如通信和观测)对基座的姿态有一定要求,因此,在轨迹规划中,应尽可能减少空间机械臂的运动对基座产生的扰动。在这方面,研究者们也取得了很多成果。文献[7,15-17]利用反作用零空间(RNS)的方法,保证基座的姿态不受机械臂运动的影响。但是,反作用零空间法仅对冗余空间机械臂是有效的,对非冗余机械臂是非常受限的。Xie等[18]利用双臂空间机器人结构,一条臂用来完成抓取等任务,另外一条臂用来补偿基座姿态扰动。部分学者们利用优化的思想,将基座姿态的干扰作为目标函数,分别利用粒子群优化算法(Particle swarm optimization,PSO)[19]和混沌粒子群优化算法(Chaos particle swarm optimiza-tion,CPSO)[5,20]获得相应的轨迹。Misra等[8]将基座姿态扰动作为目标函数的一部分,此时,轨迹规划转化成凸二次规划(CQP)问题。由于本文的研究对象为6自由度非冗余空间机械臂,故将基座姿态扰动作为目标函数的一部分。
空间机械臂的轨迹规划问题也可以转化为优化问题,如上文所提及的利用优化思想减少基座扰动。此外,为保证机械臂末端在终止时刻达到目标位姿,部分学者将空间机械臂轨迹规划问题转化为优化问题,利用高斯伪谱法[21]、差分进化算法[5]、粒子群算法[4,16,19,22]、遗传算法[23]等获得相应的轨迹。根据任务的需求,部分学者研究时间最优、能量最优的轨迹规划[24]。文献[25-27]分别针对并联机器人、移动机器人、球形机器人,研究了时间最优的轨迹规划。此外,还有部分学者研究基于多目标优化的机器人轨迹规划。文献[28]考虑路径长度、路径光滑度及安全性,对多机器人轨迹进行优化。文献[29]针对移动机器人,同时考虑运动时间、运动距离、光滑度等,对轨迹进行优化。本文在设定目标函数时,除基座扰动外,还考虑了运动时间,利用混合整数规划的混沌粒子群优化方法得到相应的轨迹。
本文主要研究6自由度空间机器人笛卡尔轨迹规划问题。在笛卡尔坐标系下,将梯形规划和正弦函数相结合,对机械臂末端的位置和姿态进行参数化。阻尼最小方差法是以牺牲机械臂各个方向的精度为代价的。因此,将机械臂末端实际位姿与理想位姿之间的误差作为是否发生奇异的标志。同时,某些特定的任务需要减小基座姿态扰动及机械臂运动时间,故将此作为目标函数的一部分。最终,机械臂轨迹规划问题转化为混合整数规划问题,并采用混合整数规划的混沌粒子群优化算法进行求解。
1 自由漂浮空间机械臂模型
1.1 运动学模型
本文所涉及的运动学和动力学参数符号如表1所示。如图1所示,空间机器人系统由基座(航天器本体)和n自由度机械臂组成。
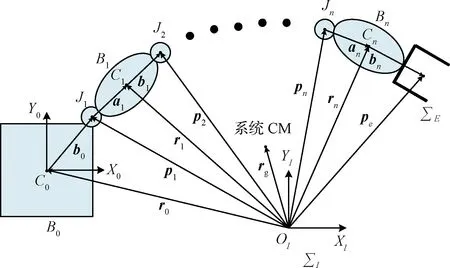
图1 空间机器人的一般模型

表1 本文所涉及的运动学、动力学参数符号
空间机器人的一般运动学可以表示为
(1)
式中:Jb和Jm分别表示与基座运动和机械臂运动相关的Jacobian矩阵。记(·)×为矩阵(·)的叉乘矩阵,E为合适维数的单位矩阵,
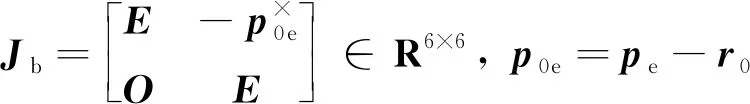

(2)

(3)
式中:Φ0为基座的姿态,Jg称为空间机器人的广义Jacobian矩阵,不仅与空间机械臂的运动学参数有关,还与动力学参数有关,因此,空间机器人的奇异被称为“动力学奇异”。
1.2 刚体的姿态表示
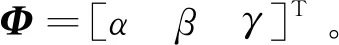
其中,sα,sβ,sγ分别表示sinα,sinβ,sinγ;cα,cβ,cγ分别表示cosα,cosβ,cosγ。即
故当cosβ=0时,矩阵Nφ奇异。
用单位四元数表示姿态,即
(4)
其中,e为旋转轴,也称为欧拉轴,ψ为绕旋转轴转过的角度。q0为四元数的标量部分,q为四元数的矢量部分,由式(4)可知,同一种姿态可以用Q与-Q两种四元数表示,但是,当限定-180°<ψ≤180°,q0≥0时,四元数表示唯一。四元数对时间的导数与角速度间的关系为
(5)
与欧拉角表示姿态相比,单位四元数法不会出现奇异,并且属于线性运算,计算效率高,运算方程简单,故本文使用单位四元数法表示基座的姿态。
2 空间机械臂的轨迹规划
本文在笛卡尔空间中规划空间机械臂末端的轨迹,使机械臂末端从初始位置pe0、姿态Φe0,连续平滑的运动到ped和Φed。在轨迹规划过程中,主要考虑回避动力学奇异、减小基座姿态扰动、减小运动时间。
2.1 轨迹的参数化
将梯形规划和正弦函数相结合,对机械臂末端的位置和姿态进行参数化。正弦函数的存在,能够达到避免动力学奇异等其他目的。

ed=ed0sinψed
即机械臂末端坐标系绕ed0旋转ψed后,姿态从Φe 0调整到Φed。
假设机械臂末端在初、末位置所在直线上运动,规划机械臂末端位置、速度,即
pe(t)=pe 0+sp(t)(ped-pe 0)
(6)
(7)
规划机械臂末端姿态时,选择适当的轨迹ψe(t),满足初始时刻ψe(0)=0,终止时刻ψe(Tf)=ψeded0,与规划机械臂末端位置、速度类似,即
ψe(t)=sψ(t)ψeded0
(8)
则机械臂末端角速度可以表示为
(9)
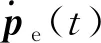
(10)
其中,f(τ)采用梯形规划,即
(11)
空间机械臂初、末端条件满足
(12)
考虑到起始时刻和终止时刻的轨迹平滑性,满足
(13)
由式(10)~(13)可得
(14)
因此,只需要确定Ap,Aψ,zp,zψ,所规划的机械臂末端轨迹便唯一确定。
与普通梯形规划不同,正弦函数的存在,能够达到避免动力学奇异、减小基座姿态干扰、运动时间等其他目的。另外,Ap=Aψ=0时,相当于普通的梯形规划,即普通梯形规划可以视为式(10)的特例。
超过95%的学生认为该教学方法可以提高学习的积极性和主动性,加深对护理程序的理解和应用,同时也增强沟通交流能力。学生赞同能培养人文关怀素养、增强团队协作能力、培养临床实践能力、培养临床思维能力、使知识掌握更牢固的比例分别为:91.5%、90.3%、93.4%、92.6%、94.1%(见表1)。
2.2 回避动力学奇异的轨迹规划
假设机械臂沿某一轨迹运动,提出一种判断是否发生动力学奇异的方法。基于此,研究回避动力学奇异的方法。
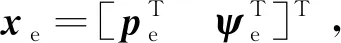
(15)
用单位四元数表示基座的姿态Q0,则
(16)

(17)
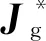
(18)

(19)
阻尼系统λ按下式进行自适应调整
(20)
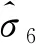
终止时刻,空间机械臂关节角及基座姿态为
(21)
(22)
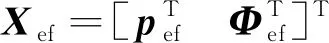

2.3 目标函数
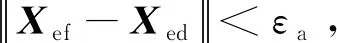
(23)
其中,Ka为权系数。Ja不仅保证了所得到的轨迹可以避免动力学奇异的发生,还可以提高终止时刻机械臂末端的精度。
由于空间机械臂受到非完整性约束,导致机械臂的运动会对基座产生扰动。最理想的情况是机械臂运动对基座姿态不产生扰动,但是对于非冗余机械臂而言,当给定机械臂末端位置和姿态的轨迹时,由式(2)可知,很难保证基座角速度ω0=0。因此机械臂轨迹规划只能在满足运动目标的前提下,尽可能的减小对基座的扰动。空间机械臂运动过程中,基座姿态相对于初始时刻在Z轴、Y轴、X轴的改变量最大分别为|Δα|max,|Δβ|max,|Δγ|max,将基座姿态扰动部分相对应的目标函数设为
(24)
式中:Kα,Kβ,Kγ分别为权系数。
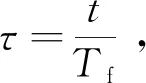
(25)
则机械臂末端运行的时间满足
(26)
运动时间相对应的目标函数为
(27)
式中:与Ka,Kα,Kβ,Kγ类似,Kt为运动时间相对应的权系数,可根据任务需求调整这些权系数。
另外,与在关节角空间轨迹规划不同,在笛卡尔空间很难满足下述要求
-θi max≤θi≤θi max,i=1,2,…,n
(28)
本文针对关节角的要求,引入惩罚函数作为目标函数的一部分,即
(29)
式中:
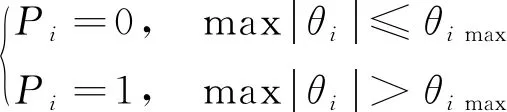
最终,本文将空间机械臂的轨迹规划问题转化为下面的优化问题
(30)
3 混合整数的混沌粒子群优化算法
3.1 整数变量的处理
由于zp,zψ的取值为正整数,因此优化问题(30)为混合整数规划问题,无法直接用粒子群优化算法进行求解。本文处理混合整数规划问题的基本思路是将在[0, 1]区间运动的粒子与整数空间相对应,将混合整数规划的问题转化为普通优化问题。
将粒子yp,yψ∈[0, 1]与zp,zψ按照一定规则进行对应。假设zp,zψ满足
(31)
其中,ap,aψ,lp,lψ为整数,则lp,lψ分别为zp,zψ可能取的整数的个数,令
(32)
其中,[x]表示不小于x的最小整数。此时,zp,zψ取
(33)
这样在[0, 1]区间运动的粒子就与整数对应起来。故此时优化问题(30)转化为
(34)
所受约束与式(30)相同。
3.2 粒子群优化算法
粒子群优化方法(PSO)不需要交叉、选择和变异,具有计算简单、易实现、控制参数少以及实数化编码等优点。
PSO将每个个体看作为一个粒子,粒子没有体积和重量,每个粒子由一个速度决定其在解空间的运动方向和距离。
假设在D维解空间中,一个群体由M个粒子组成,第l个粒子在D维解空间中的位置表示为xl,速度为vl,每个粒子所经历的最好位置为Pb l,对应的适应值为Gl best,全局所经历的最好位置为Pbg,对应的适应值为Gbest,则根据PSO,每个粒子在每一步迭代中根据下式更新速度和位置:
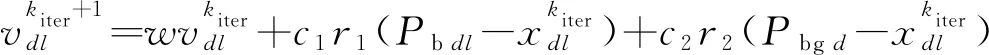
其中,kiter为迭代次数,w为惯性因子,c1和c2为学习因子,常取[0, 4]内的常数,r1和r2为[0, 1]内均匀分布的随机数。为了改善算法的收敛性能,本文采用Musaed所提出的惯性因子w的形式[30]。
一般终止条件设定为达到最大迭代次数或者Pbg已经满足一个预设最优适应值。
3.3 混沌粒子群优化算法
粒子群算法一直在局部最优位置搜索,而丧失了全局最优位置搜索的能力时,算法发生“早熟”的情况。因此,本文采用混沌粒子群算法(CPSO),通过混沌运动的随机性和遍历性,保证粒子群体的多样性,改善粒子群算法摆脱局部最优的能力。
CPSO的基本思想是在每步迭代过程中,以当前最优位置为初始位置,通过混沌序列产生新的群体,若新的群体中最优粒子优于当前最优位置,则将新群体中的最优粒子代替当前最优位置,如图2所示。在局部最优位置周围通过混沌序列进行搜索,可有效避免群体陷入局部最优位置,并快速找到全局最优位置。
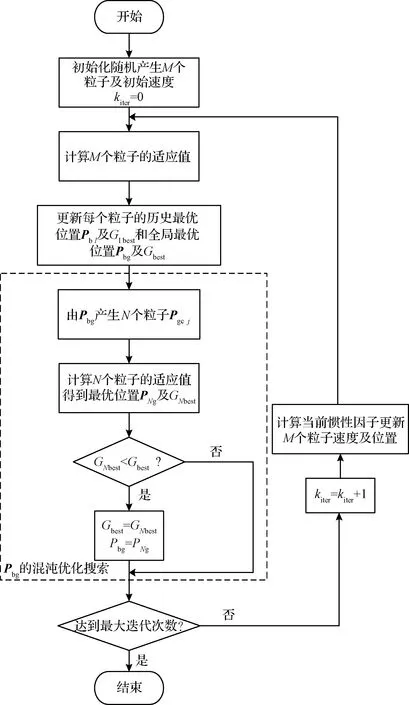
图2 CPSO的流程图
通常,利用Logistic方程产生混沌序列
zi+1=μzi(1-zi),i=0,1,2,…
(35)
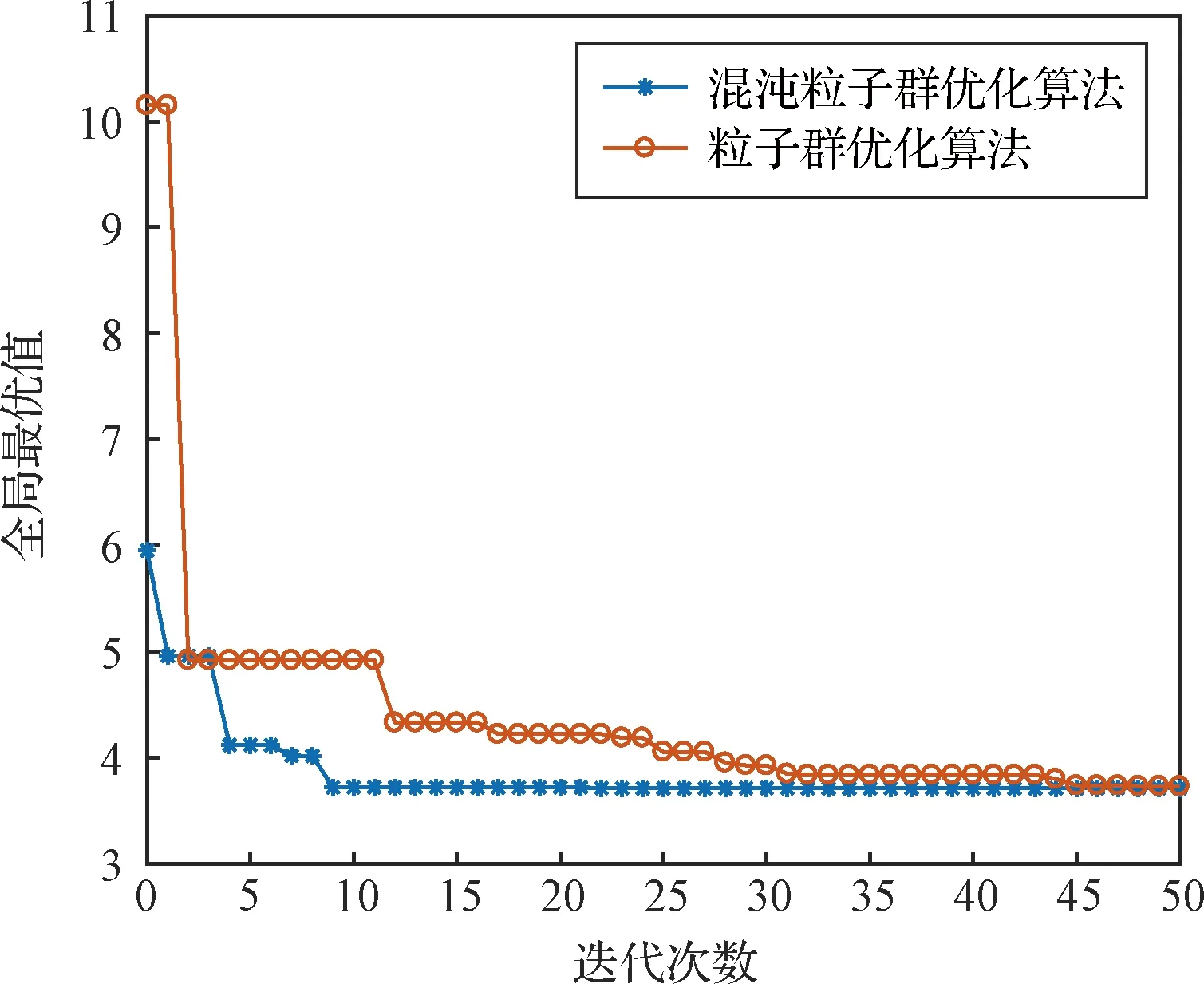
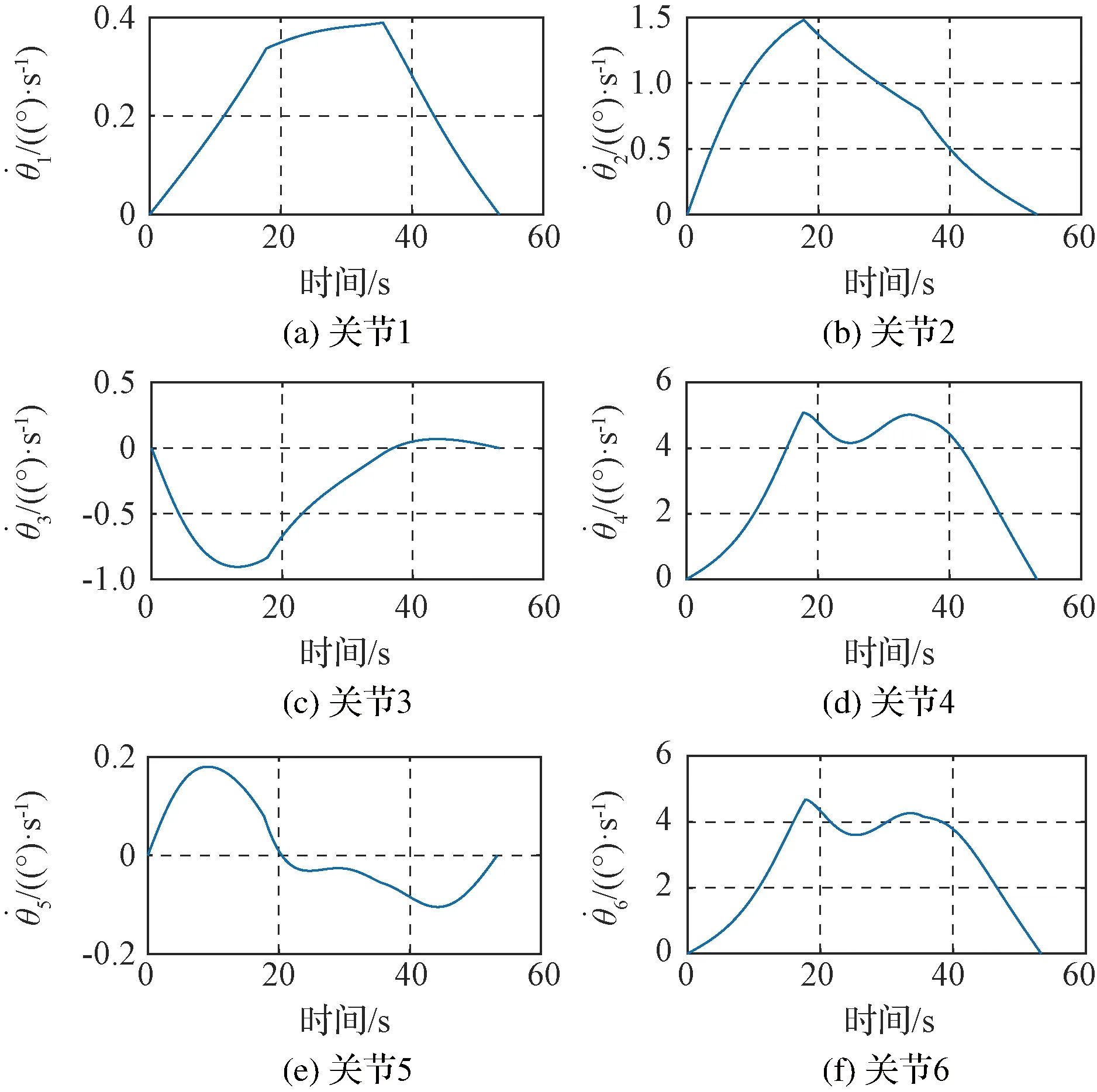
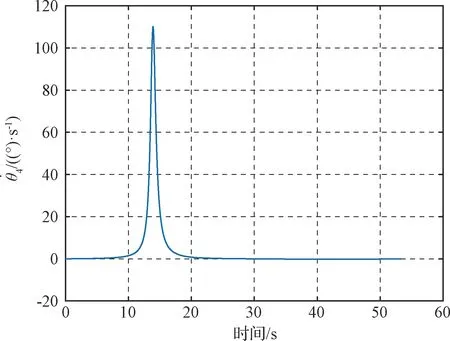
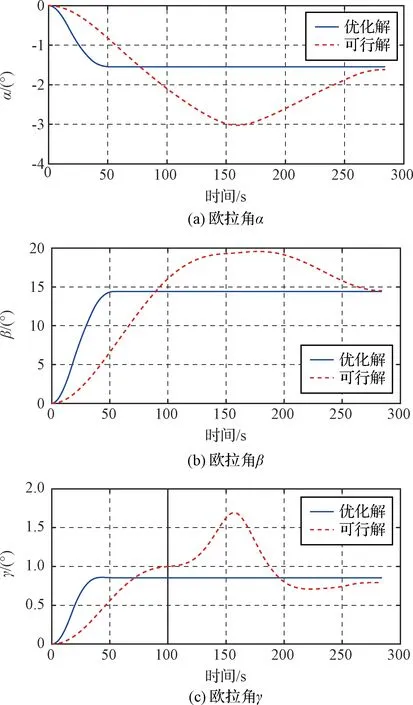
当0 采用CPSO进行优化的基本步骤如下: (1) 初始化算法参数,令kiter=0,随机产生M个粒子,每个粒子具有D个未知参数,构成粒子种群,并随机生成M个粒子的初始速度。 (2) 将M个粒子的位置代入目标函数中计算得到各自的适应值。 (3) 更新每个粒子的历史最优位置Pb l以及全局最优位置Pbg。 (4) 对Pbg进行混沌优化搜索 Pc dj=ad+zdj(bd-ad) (36) ad,bd分别表示粒子第d维取值的下限和上限。再由Pbg和Pc j产生Pgc j,并作为新群体的N个粒子, (37) 将此N个粒子代入目标函数中计算得到各自的适应值,新群体的最优位置为PNg,对应的适应值为GNbest,若GNbest (5) 计算当前惯性因子的数值,更新M个粒子的速度及位置。 (6) 判断是否满足终止条件,满足则终止计算,否则返回步骤(2)。一般终止条件设定为达到最大迭代次数或者Pbg已经满足一个预设最优适应值。 表3 空间机械臂关节角参数范围 表2 空间机器人质量特性 初始时刻,机械臂末端的初始位姿为 机械臂的关节角及基座的姿态为 终止时刻,机械臂末端的位姿为 仿真中,阻尼最小方差法 目标函数的权系数分别为 混沌粒子群优化算法处理优化问题,搜索到的最优解为 (38) 对应的目标函数为 J*=3.7112 机械臂运动时间为Tf=53.3107 s,机械臂运动过程中,相对初始时刻,基座姿态在Z轴、Y轴、X轴上最大改变量分别为|Δα|max=1.55°,|Δβ|max=14.3957°,|Δγ|max=0.8591°。 普通粒子群优化算法和混沌粒子群优化算法每迭代一次得到的全局最优值如图3所示。两种优化算法虽然在最后得到的全局最优值相近,但是由图3可知,普通粒子群优化算法需要迭代45步左右得到全局最优值,而混沌粒子群优化算法仅需迭代10步便可以得到最优值。因此,混沌粒子群优化算法能够提高收敛速度。 图3 PSO和CPSO算法最优值的变化曲线 将混沌粒子群算法得到的参数(39)代入式(7)、(9)、(15)中,可以得到规划的机械臂关节角、角速度的曲线如图4、图5所示。由图4可知,关节变化平缓,且关节角在表3范围内变化。由图5可知,关节角速度大小均不超过5 (°)/s,不存在角速度突变的情况。 图5 空间机械臂关节角速度 图4 空间机械臂关节角 当Ap=Aψ=0,即采用普通梯形规划时,空间机械臂关节4的角速度如图6所示。在14 s时机械臂发生空间动力学奇异,关节4的角速度超过100 (°)/s,造成轨迹规划失效。因此,与普通梯形规划相比,本文提出的轨迹规划方法可以避免机械臂在运动过程中发生动力学奇异。 图6 普通梯形规划的关节4角速度图像 为了验证对基座姿态扰动及运动时间的优化效果,选取一组未经基座姿态扰动及运动时间优化的可行解,即将目标函数设定为J=Ja+Jpenalty,其他条件均不变,在利用混合整数规划的混沌粒子群优化算法时,适应值小于1迭代结束。此时,Ap,Aψ,zp,zψ的取值如下, Ap=2.966,Aψ=-0.2643,zp=1,zψ=2 本文对比了优化解及可行解对应的基座(航天器本体)姿态扰动,如图7所示。运动过程中,基座姿态扰动在Z轴、Y轴、X轴上最大值分别为[1.55°, 14.3957°,0.8591°]和[3.0240°, 19.5565°,1.6947°]。所需的运行时间分别为53.3107 s和284.0907 s。由此可知,不仅可行解的运行时间要长于优化解的运行时间,而且在姿态扰动方面,优化解也要优于可行解。因此,空间机械臂对基座姿态扰动及运行时间的轨迹优化是有效的。 图7 基座姿态扰动 本文研究在笛卡尔坐标系下的空间机械臂轨迹规划。结合梯形规划和正弦函数,将空间机械臂末端位置和姿态进行参数化。假设机械臂沿着某一轨迹运动,根据阻尼最小方差法的特点,提出一种判断是否发生动力学奇异的方法。将基座姿态扰动与运动时间作为目标函数的一部分,最终轨迹规划问题转化为多目标优化问题,并利用混合整数规划的混沌粒子群优化方法进行求解。本文所提出的轨迹规划方法简单,易于求解。将获得的轨迹代入到空间机械臂系统中进行仿真,结果表明本文所提出的算法是有效的。与普通梯形规划相比,本文提出的规划方法能够避免机械臂运动过程中遇到动力学奇异。针对基座姿态扰动和机械臂运动时间,优化轨迹明显优于可行轨迹,从而说明了机械臂轨迹优化算法的有效性。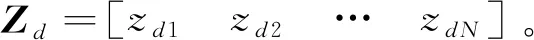
4 仿真校验


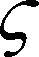

5 结 论

