利用函数不等式解高考函数题的策略分析

摘 要：在近几年的高考题中，活跃着一类与自然底对数有关的不等式，其中有一部分题目通过等价变形最终可以转化为常见的对数函数不等式：1-1/x≤lnx≤x-1（x>0）（以下统一称之为对数函数不等式）。这类问题因综合性强、立意新颖、构思巧妙、技巧性高等特点愈加得到命题者的青睐，且常作为各类试卷的压轴题出现，但学生往往因为理不清条件之间的关系，找不到解决问题的入口而陷入困境，文章拟对这类问题加以探究、总结，希望找到解决这些问题的规律，并对教师课堂教学形成一定的启发。浅薄观点，敬请同行指正。

关键词：函数不等式;高考;函数题

一、 知识理解

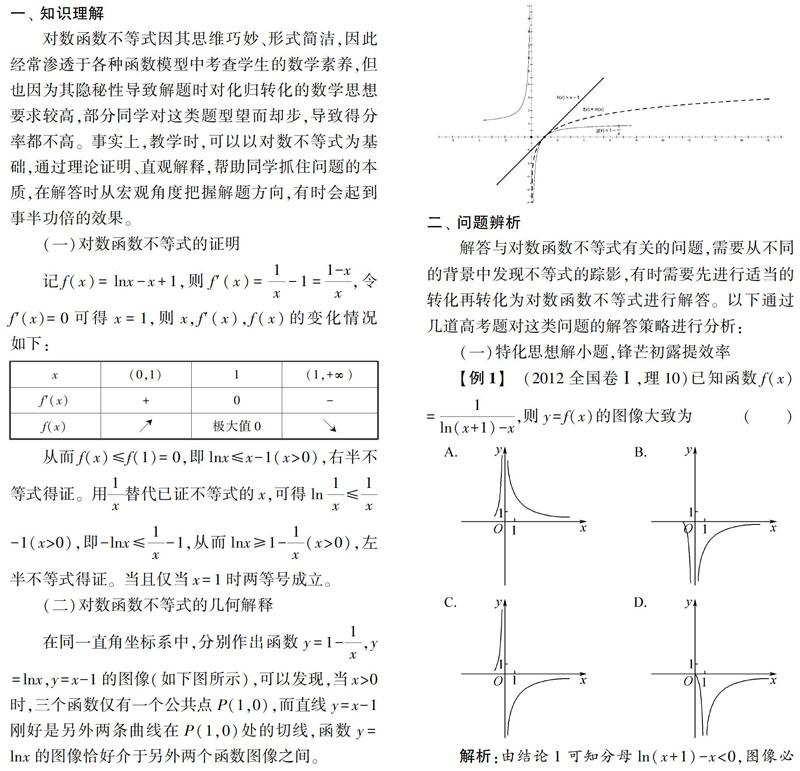
对数函数不等式因其思维巧妙、形式简洁，因此经常渗透于各种函数模型中考查学生的数学素养，但也因为其隐秘性导致解题时对化归转化的数学思想要求较高，部分同学对这类题型望而却步，导致得分率都不高。事实上，教学时，可以以对数不等式为基础，通过理论证明、直观解释，帮助同学抓住问题的本质，在解答时从宏观角度把握解题方向，有时会起到事半功倍的效果。

点评：本题为2013全国新课标Ⅱ卷的压轴题，不仅考查函数、不等式等有关的传统知识和方法，而且还考查导数等工具的掌握和灵活运用。本题第（1）问设计数形结合思想，从而迅速求得f（x）的单调区间，但第二问若用同样方法或者通过构造函数寻找最值证明，显然碰到了复杂运算，其中f′（x）=0更是超越方程，一般无法直接求解。但若用对数函数不等式证明，思路明确，过程简捷，淡化繁难技巧，解法过程一气呵成，真正实现“大题小做”，数学之精妙溢于言表。因此本题可充分考查考生的数学思维品质，符合新课改的精神，是难得的好题。

数学问题千变万化，解法灵活多变，即便是同一道题，也有多种解题切入点。教师在追求问题能被解决的同时，不要拘泥常法、不恪守常规，应善于開拓、变异、发散，从多角度、多方位、多途径进行解答，合理运用转化思想，寻找最优途径。如文章例3、例6从正面直接入手很难取得突破，而如果对问题的形式稍做转化，从侧面入手，问题便会迎刃而解，因此在解题中我们需要灵活应用转化思想，从而达到化难为易、化繁为简、化未知为已知、化陌生为熟悉的目的。适时地进行一题多解的展示，能培养学生的思维能力、激发学生的探究热情，同时这些解题策略和方法之间必定有繁简优劣之分，教师在讲评时引导学生对比分析，一定能加深学生的体会，从而优化学生的解题思路和解题方法。而所有的这一切都是为了形成探索性的学习方式，培养学生的创新意识和实践能力。

总之，数学题目是永远出不完，也是永远做不完的，但是，如果善于运用变式，在变式中掌握一类问题的解法，则会以少胜多，大大提高教学的效率、消除和防止因思维僵化、想法呆板而带来的问题。如，文章中对数函数不等式的三个变形体现的是同一个数学本质（几何解释可说明），但形式的差异可以激发学生学习数学的兴趣及对数学本质的理解，从而在解决不同类型的题目时能以不变应万变。当然，变式不宜太多，否则学生将会陷入对数量繁多的变式的辨析中，忽视了知识的本质，难以掌握知识的来龙去脉。建议在教学中安排的例题、习题的变式时应注意设计结论的发生情境，重视公式、结论等的形成过程，让学生自己去归纳概括。这不仅加深了学生对公式、结论的认识和记忆，而且能提高学生的概括水平、思维能力，提高数学思维的品质。

点评：本题是2011年普通高考湖北理科试卷压轴题（第21题），以函数不等式立意，主要考查函数、导数、不等式的证明等基础知识，同时考查综合运用数学知识进行推理论证的能力，渗透化归、转化的思想。题目起点低，落点高，综合性强，通过三个问题逐层推进，难度逐步提高，全面检测考生的观察、试验、联想、猜测、类比、探究等思维品质，考题蕴含丰富的潜在价值。解法中对数函数不等式的使用可谓匠心独运，数学简捷美的本质所带来的震撼令人意犹未尽。

参考文献：

[1]李洪洋.不等式“搭台” 导数“唱戏”[J].中学数学·高中版，2009（3）：27-30.

[2]方亚斌.ex的幂级数展开式演绎高考题[J].数学通讯·下半月，2012（2）：50-53.

[3]江志杰.基于数学解题变式的高三教学主张[J].中学数学教学，2013（1）：24-58.

[4]周超.构造函数巧解题[J].数学通讯·下半月，2013（6）：33-34.

作者简介：

王成焱，福建省厦门市，福建省厦门双十中学。