掀开情境面纱 建构物理模型
张晓斌
(福安市第一中学,福建 福安 355000)
随着2017 版普通高中课程标准的颁布,高考内容改革随之全方面推进,“一体四层四翼”深入人心。“知识立意、能力立意、素养立意”成为高考命题实现考查目标的依据。物理学科的5 个关键能力,其中一个便是模型建构能力。20 世纪初,国外就有许多学者开始研究模型以及模型教学,这些研究也在启发着国内学者。近年来国内学者结合我国教学的特点也对模型教学进行了深入的探索与研究。通过知网数据库在基础科学的物理学中搜索关键词“模型”,发现有48734 条相关文献,在基础教育期刊(高中)中搜索主题“物理模型”,发现有3700 条相关文献,由此可知物理模型建构一直以来都是研究焦点。
一、问题的提出
模型建构能力是物理教学中培养学生的关键能力之一,对促进学生理解科学知识、科学方法以及科学本质具有深刻意义。2019 年出版的《高考评价体系说明》中明确提出“基于已有的实证调研和文献分析研究结果,高考通过设置不同层级的情境活动来考查学生在‘四层’内容上的表现水平”。因此如何剖析不同层级的情境将物理模型建构出来就是解决物理问题的一个重要突破口。《高考评价体系说明》将情境分成两类“生活实践情境”和“学习探索情境”,前者与物理中的模型关联大,考查学生的科学思维素养,后者则强调科学探究素养。高考题如何体现情境,解题时考生又如何拨开情境建立模型解决物理问题?本文将从“生活实践情境”出发,以高考题为例分析“去情境、建模型”。
二、剖析“生活实践情境”,建构物理模型
自物理模型提出以来,就有大量的教师、学者对模型进行分类。其中黄书鹏、汪崇渝、张滨等人将物理模型分为两种:理想模型和实物模型。理想模型包含了对象模型、条件模型、过程模型、理论模型以及问题模型。[1]对象模型往往作为一个支点以研究对象的形式穿插在其他模型中,例如质点、点电荷等。理论模型则常在天体运动中考查,例如宇宙大爆炸理论,黑洞模型等;考查最多的则是条件、过程、问题模型,这些模型与日常生活以及生产实践密切相关,考查学生运用所学知识解释生活中的现象、解决生产实践中的问题的能力。
基于情境的复杂程度,高考评价体系中的情境活动可以分为两层。第一层是简单的情境活动。此类情境活动中,需要启动的是单一的认知活动,即面对问题时只需要调动某一知识点或某种基本能力便可解决。因此,通过这类情境测评出的是学生基本的知识和能力水平。第二层是复杂的情境活动。此类情境活动涉及的是复杂的认知活动,主要考查学生综合运用知识和能力应对复杂问题的水平。
(一)生活实践情境中的条件模型
条件模型是指舍去问题中的次要因素,抓住主要因素,分析问题的本质,将研究对象的外部条件理想化建立简单的物理模型。例如:光滑、轻绳、轻杆、轻弹簧、弹性正碰等条件模型。
[例1]2019 年全国III 卷第16 题:用卡车运输质量为m 的匀质圆筒状工件,为使工件保持固定,将其置于两光滑斜面之间,如图1 所示。两斜面I、Ⅱ固定在车上,倾角分别为30°和60°。重力加速度为g。当卡车沿平直公路匀速行驶时,圆筒对斜面I、Ⅱ压力的大小分别为F1、F2,则
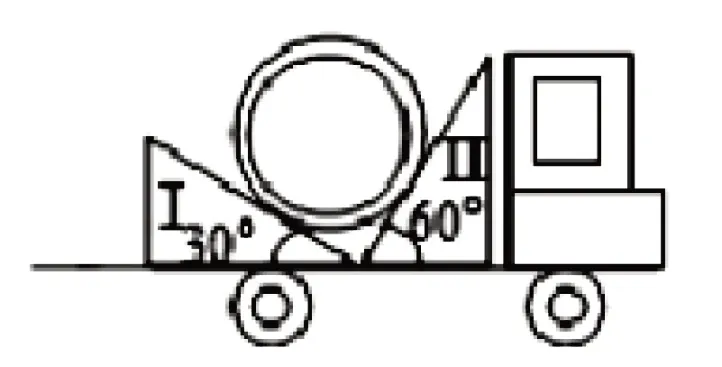
图1
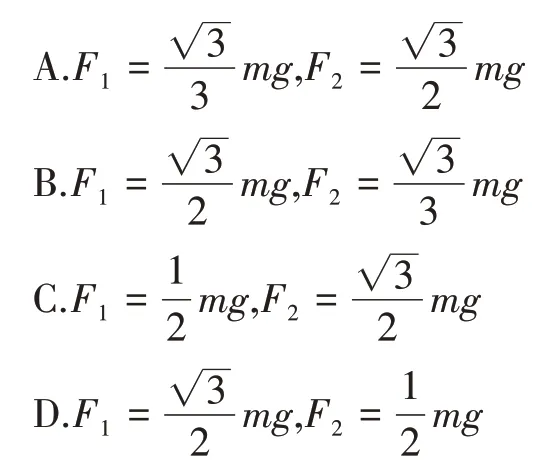
[答案]D
[情境与模型]
本题依托在卡车运输工件的生活情景中,将实际生活中的外部条件理想化,创设了一个斜面光滑的条件模型。在解决物理问题时又忽略圆筒形状和大小将圆筒看作质点,建立了质点模型。此时再对圆筒受力分析便可得出此题要考查的知识点为三个共点力的平衡问题。知道考点结合数学中的几何知识便可得出圆筒所受支持力与重力的关系,由此找到本题突破口。此类情境属于第一层简单情境,只需调动共点力平衡的知识利用三角函数关系便可求出相应的物理量。
(二)生活实践情境中的过程模型
过程模型顾名思义就是将物理过程建立一个模型来分析。在建立模型时需将一个复杂的过程根据研究问题的需要忽略次要因素抓住主要因素进行理想化后抽象出一个相对简单的物理过程。例如:匀变速直线运动模型、匀速圆周运动模型、简谐运动模型等。
[例2]2019 年全国I 卷第18 题:如图2 所示,篮球架下的运动员原地垂直起跳扣篮,离地后重心上升的最大高度为H。上升第一个所用的时间为t1,第四个所用的时间为t2。不计空气阻力,则满足
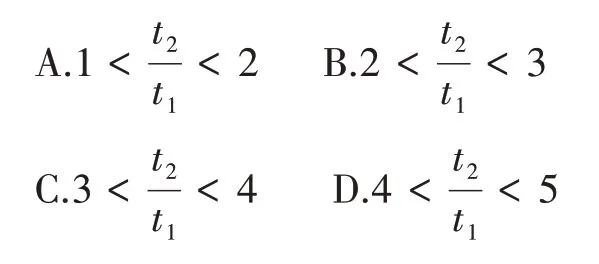
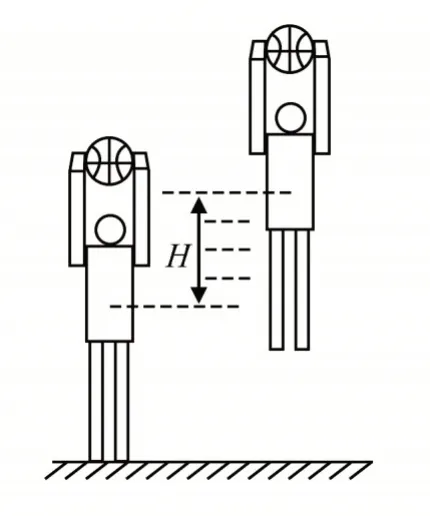
图2
[答案]C
[情境与模型]
本题依托在篮球架下的运动员起跳扣篮的情境下,将实际扣篮运动理想化成垂直起跳,不计空气阻力,建构了一个竖直上抛运动的过程模型,而竖直上抛运动到达最高点的逆过程是初速度为0 的匀加速直线运动模型。根据初速度为0 的匀加速直线运动,相邻相等位移的时间比为1:
则可得出答案。此类情境属于第二类复杂情境,此题除了建构出竖直上抛模型,还要晓得竖直上抛到最高点的逆过程是自由落体,并结合相应的比例式进行综合分析才能得到正确的选项。
(三)生活实践情境中的问题模型
问题模型反映了特定的物理问题、事物结构以及物理本质,蕴含解决这类物理问题的物理知识、方法以及技巧,提供了解决这类问题的一般思路与步骤。[2]例如:板块问题模型、连接体问题模型、汽车追及与相遇问题模型、传送带问题模型等。
[例3]2015 年全国II 卷第25 题:下暴雨时,有时会发生山体滑坡或泥石流等地质灾害。某地有一倾角为θ=37°(sin37°=0.6)的山坡C,上面有一质量为m的石板B,其上下表面与斜坡平行;B 上有一碎石堆A(含有大量泥土),A 和B 均处于静止状态,如图3 所示。假设某次暴雨中,A 浸透雨水后总质量也为m(可视为质量不变的滑块),在极短时间内,A、B 间的动摩擦因数μ1减小为,B、C 间的动摩擦因数μ2减小为0.5,A、B 开始运动,此时刻为计时起点;在第2s 末,B的上表面突然变为光滑,μ2保持不变。已知A 开始运动时,A 离B 下边缘的距离l=27m,C 足够长,设最大静摩擦力等于滑动摩擦力。重力加速度大小g 取10m/s2。求:
(1)在0~2s 时间内A 和B 加速度的大小;
(2)A 在B 上总的运动时间。
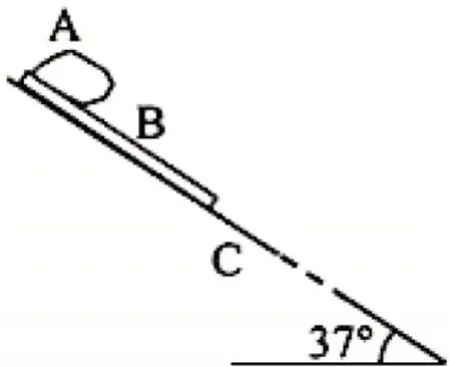
图3
[答案](1)A 和B 加速度的大小分别为3m/s2和1m/s2;(2)A 在B 上总的运动时间为4s。
[情境与模型]
本题依托在暴雨时的泥石流或山体滑坡的自然情境中,理想化泥土和石板,建构了一个板块问题的模型。此模型考查了牛顿运动定律的综合应用和匀变速直线运动的位移与时间的关系,对学生建构的板块模型多过程的分析要求高,思维量大。此类情境属于第二类复杂情境,此题建构出的板块模型本就属于高中知识的难点部分。此题情境多变,过程多样,要求学生冷静分析,很好地考查了学生的理解能力、推理论证能力、模型建构能力。
三、明确关键词拨开情境建模型
情境作为串接金线(核心功能)和银线(能力素养)的载体已在高考命题当中体现出来。物理模型的建构是基于真实的生活情境,因而要想拨开情境就要明确物理模型的基本特征。从情境的切入模型的建构都离不开审题过程中对关键词的分析。
条件模型特征对应的关键词如:“匀质”“光滑”“轻绳”“轻杆”“轻弹簧”“弹性正碰”等;过程模型特征对应的关键词如:抛体运动中的“忽略空气阻力”、圆周运动的“圆轨道”等;问题模型特征对应的关键词如:板块问题模型的“滑块与木板”、传送带问题模型的“传送带”、行星共线问题的“冲日、凌日、合日”等。
简而言之,我们可以将拨开情境建模性的过程用下图4 简单表示出来。
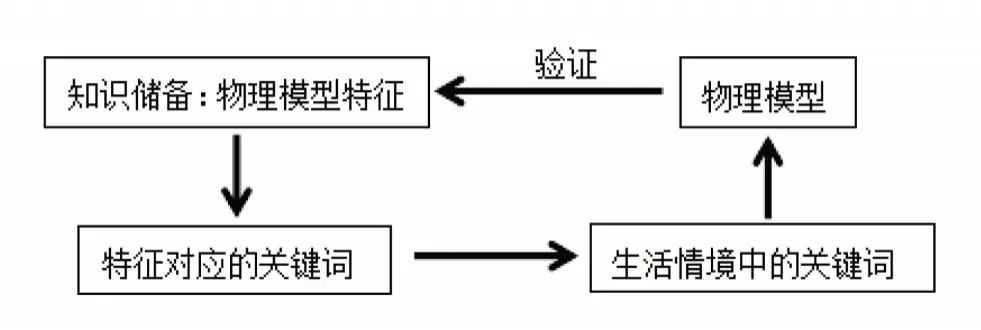
图4
四、结语
高考以生活实践问题情境与学习探索问题情境为载体,回归人类知识生产过程的本源,还原知识应用的实际过程,符合人类知识再生产过程的规律。通过对情境的分析忽略次要因素,抓住主要因素,建立物理模型不仅可以对物理知识有更深刻的理解,同时让学生从解题向解决问题转变,感受物理知识在生活中的应用。因此在高中物理课程教学中,显化物理科学模型的教育,将会提高教师的教学水平,发展学生的综合能力。

