解题教学中学生高阶思维的培养

陈惠增

（福清市高山育才中学，福建 福清 350319）

初中数学解题教学中存在的问题：没有设计好问题串，对解题只分析求解，没有进行题后反思；只对题目进行多解罗列，没有进行优解的归纳；过于定势思维的解题预设，没有提出质疑与批判.这样的解题教学，学生的思维处于“低价”状态，具体表现为：不可变通性，缺乏深刻性，不成结构性，缺少批判性（即质疑能力）.造成上述问题的主要原因：教师解题教学观念过时、解题教学视野局限、解读题目肤浅、解题过程功利等.这样可能阻碍培养学生高阶思维能力，从而影响学生数学素养的提升.因此，改变解题教学方式是突破低阶思维，培养学生数学高阶思维，拓展学生数学思维空间，提高学生的解题能力，提升学生数学解题素养的必然选择.

一、高阶思维及特点

思维是大脑在面对刺激时所进行的一连串活动（Udall&Daniels，1991），Anderson认知目 标分类学（2001）如图1.

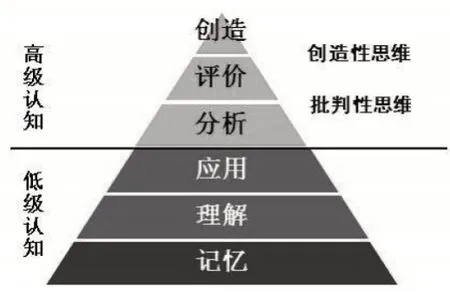
图1

所谓高阶思维，是指发生在较高认知水平层次上的心智活动或认知能力.它在教学目标分类中表现为分析、评价和创造.高阶思维是高阶能力的核心，主要是指创新能力、问题求解能力、决策力和批判性思维能力.高阶思维能力集中体现了数学学科素养的新要求，是适应知识时代发展的关键能力，发展高阶思维能力是数学课堂教学的应然追求。

高阶思维能力是新时代人才发展的必备修养，其表现为思维的层次性、整体性、创新性、批判性等.教师在开展解题教学时，需要结合这些思维特点来进行解题教学，以推动初中学生高阶思维能力的形成和发展.从心理学角度来看，智力的核心是思维能力，高阶思维能力越强，创新能力也就越强；从社会学角度看，人类的三次科学技术革命，均是由有高阶思维能力的人推动的.

二、解题教学中培养学生高阶思维的方式

数学教学中注重发展思维是学生能力培养的核心，而培养学生的高阶思维能力，对于数学素养的提升和数学关键能力的提高，无疑起到了一定的促进作用.基于目前初中数学解题教学存在的问题，如何在解题教学中培养学生的高阶思维？本人从初中数学解题教学的实践出发，提出以下几点.

（一）设置问题串——培养高阶思维的层次性

问题是思维的起点，设置有层次、有梯度的问题，让学生在思考每个问题的过程中不断深入，从而通过解决这样的问题，达到培养学生层次性的高阶思维.

例如：已知a＋b＝5，ab＝3，求a2＋b2的值.（人教版教材八年级上册P112.7）

问题1 已知a＋b＝5，ab＝3，求（a－b）2的值.

问题2 已知a＋b＝5，ab＝3，求a－b 的值.

问题3 已知a＋b＝5，ab＝3，求a2－b2的值.

问题4 已知a＋b＝5，ab＝3，求a2＋b2的值.

问题5 已知a＋b＝5，ab＝3，求a3＋b3的值.

问题6 已知a＋b＝5，ab＝3，求a4＋b4的值.

问题7 已知a＋b＝5，ab＝3，求a5＋b5的值.

从已知条件出发，有层次地设置问题，所求的结论从简单到复杂，层层递进，满足不同层次的学生的需求，通过这样问题串设置，培养学生从低阶到高阶的思维.

（二）通过题后反思——培养高阶思维的整体性

“题后反思”，是指解题完成之后，对解题分析过程中所涉及的知识，解题的方法，解题策略或模型的归纳总结.

例如：如图2，在网格纸中，每个小正方形的边长为1，A，B，C，D 为格点，线段AB，CD 交于点E，则sin∠AEC 的值为（ ）

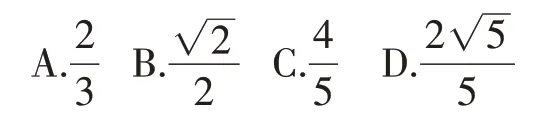
略解分析：解法1（高中公式tan2α＝

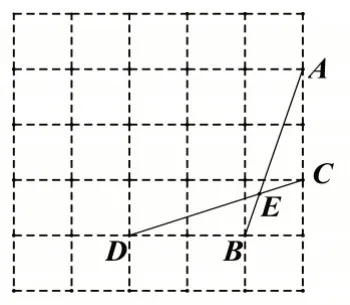
图2

如图3，设格点F，连接AD，BF，

则∠AEC＝2∠BAD，

在Rt △ABF中，tan ∠BAD＝

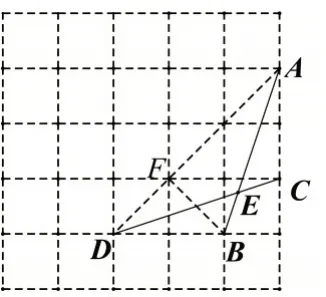
图3

所以sin∠AEC＝.故选C.

解法2：如图4，连接DF，CF，DH，过点F作FG⊥CD于点G，DF∥AB，则∠AEC＝∠FDC，

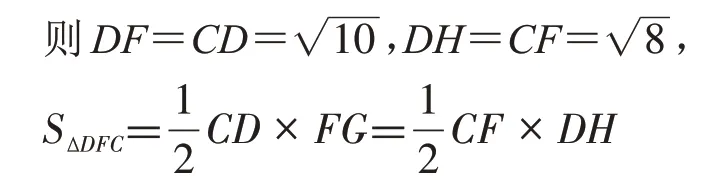
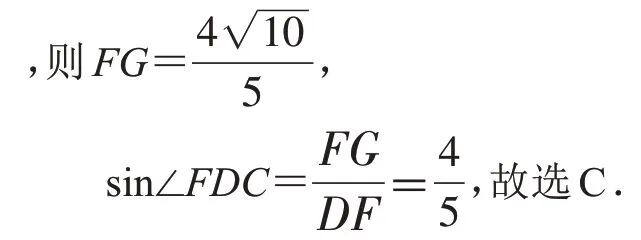
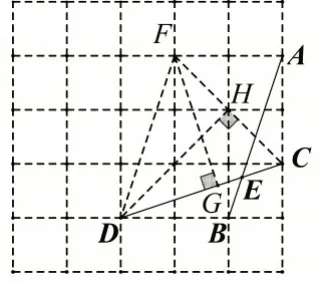
图4

解法3：如图5，连接AD，BC，则BC∥AD，

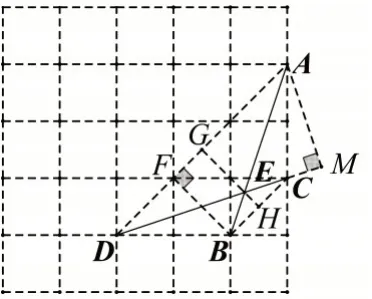
图5

题后反思：1.知识层面：本题所涉及的知识有哪些？从不同的解法中归纳应用到的知识有哪些？

2.方法层面：解法1 是从高中2 倍角公式直接应用而求解，简单明了，但是超出要求；

解法2，用添加辅助高线，通过等面积法求解；解法3 用相似及等面积法求解.

总之，求解锐角三角函数的值的两种基本思路：其一是用三角函数的思想求解，即当知道锐角的度数（特别是特殊角度）时，可直接得出其三角函数值；其二是用几何定义法，即构造直角三角形，通过所对应边的比而求值.

3.策略（模型）层面

（1）如图6，倍长矩形MDEC，倍长矩形AFBG中，∠AEC＝∠MHC＝∠DHE＝∠AJG是倍长矩形的模型特征（两对角线夹角锐角的正弦值）.

（2）网格中的问题，从几何构造角度，应该是多连接一些线，放大图形（全局角度）.

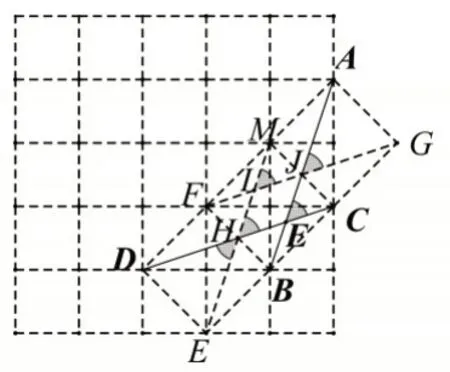
图6

解题教学中，不但要进行解题分析与求解，更重要的是题后反思，这样才能培养学生思维的全面性（整体性），使学生从多个角度认识解题及归纳，达到培养学生高阶思维的目的.

（三）通过多解选优——培养高阶思维的创新性

创新意识与创新能力是培养新时代人才的要求.要创新，就必须先开发思维.数学解题教学中，充分发挥习题潜在的功能，有意识引导学生从不同角度、不同层次去思考与分析，从而培养学生的高阶思维的创新性.

例如：如图7，a∥b∥c，a 与b 之间的距离为3，b 与c 之间的距离为6，a，b，c 分别经过等边△ABC 的三个顶点，则此三角形的边长为__________________.

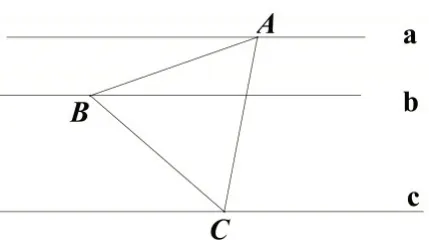
图7

解法1：如图8，过点A作AD⊥C于点D，过点B作EF⊥a于F，作EF⊥a于点E，则矩形AFED，BF＝3，BE＝6，AD＝EF＝9，DE＝AF.

设AB＝AC＝BC＝x.

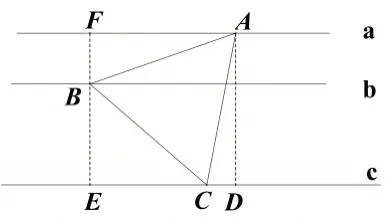
图8

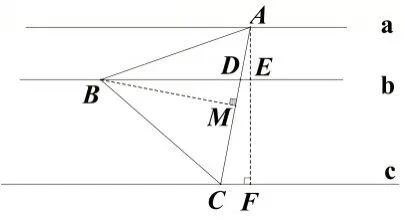
图9

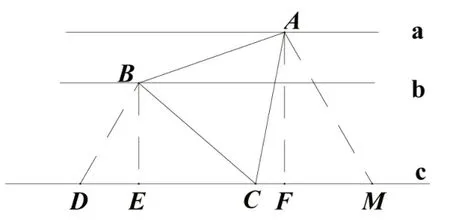
图10

解题教学过程中，教师要引导学生进行思考，解法1，对于解含三个根号的无理方程，应该通过两次平方才能达到化去根号的目的，在这种情况下，引导学生上式的等式进行移项变形后：计算会更简便些.通过对比，发现化成差式相对来说计算量会小些.解法1 列方程相对容易，但解方程很难，超出《义务教育数学课程标准（2011 年版）》的要求，此时，教师可引导学生思考，能否通过其他方式列简单方程来达到求解的目的？引导学生进行多解思考，达到多解优选的目的，从而可能产生类似解法2 的思路；继续引导学生再思考，能否不用列方程，就能直接求解呢？可能又如解法3，通过构造“一线三等角”的模型可直接求解.解题过程中，教师不断引导学生思维升华的思考，这就是高阶思维的创新性的体现.

（四）通过打破预设——培养高阶思维的批判性

批判性思维是高阶思维能力的重要组成部分.建构主义认为“应把错误看成学习的一个资源”，学生可以通过“错误”引发认识冲突，促进对自己思维过程的批判性思考.

例如，若两个正方形的边长比是3：2，其中较大的正方形的面积是18，则较小的正方形的面积是（ ）

A.4 B.8 C.12 D.16

此题的正确答案是C，而有部分学生选择了B 的错误答案，教师在错因分析中，总认为学生是因为把两个正方形的面积比误认为等于它们的相似比，其实深入了解学生之后，发现有部分同学是因为计算“32＝6”错误而导致的，即对于这种错误的原因分析，可了解真实情况，针对性地配置相应的练习.引导学生对错因分析的同时，启发学生发展批判性的思考：“我为什么会错？怎样防止下次再错？”

在解题教学中，还可以打破原有的提示进行批判性的思考.

例如：人教版教材八年级下册P29 第14 题.

如图11，△ACB 和△ECD 都是等腰直角三角形，CA＝CB，CE＝CD，△ACB 的顶点A 在△ECD 的斜边DE 上.求证：AE2＋AD2＝2AC2.（提示：连接BD）

证明：如图12，连结BD，因为△ACB和△ECD是等腰直角三角形，

所 以∠ACB＝∠ECD＝90°，CA＝CB，CE＝CD，∠CED＝∠CDE＝45°.

又因为∠ACB＝∠ACD＋∠BCD，∠ECD＝∠ACD＋∠ACE，

所以∠ACE＝∠BCD.则△ACE≌△BCD.

所以∠CED＝∠CDB＝45°，AE＝BD.则∠ADB＝∠CDE＋∠CDB＝90°.

在Rt△ADB与Rt△ABC中，

AB2＝BD2＋AD2＝AE2＋AD2，AB2＝AC2＋BC2＝2AC2，

即AE2＋AD2＝2AC2.

课本为了降低题目求解的难度而出现提示，但教师在解题教学中，可提出如若不按提示证明，可否有其他的解法呢？这样放飞学生的思维，学生就可能想出如下的证明方法：

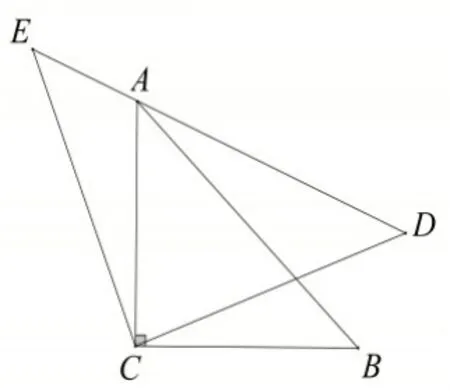
图11

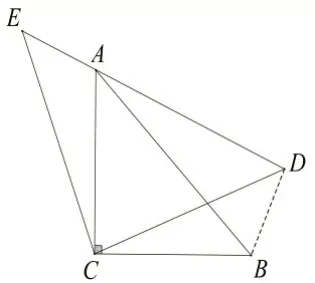
图12

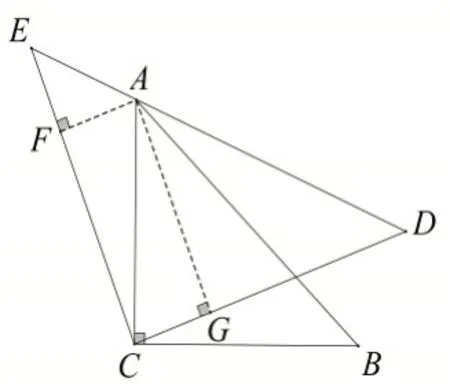
图13

证明：如图13，过点A分别作AF⊥CE，AG⊥CD，垂足分别为F，G.

则∠AFE＝∠AFC＝∠AGC＝∠AGD＝90°，

因为△ECD是等腰直角三角形，

所以∠ECD＝90°，∠CED＝∠CDE＝45°.

则四边形AFCG是矩形，即AF＝CG.

在△AEF和△ADG中，

由于∠AFE＝∠AGD＝90°，∠CED＝∠CDE＝45°，

则∠EAF＝∠GAD＝45°，即AF＝EF，AG＝DG.

在Rt△AEF与Rt△AGD中，

AE2＝AF2＋EF2＝2AF2＝2CG2，AD2＝AG2＋DG2＝2AG2，

在Rt△ACG中，

由 于AC2＝AG2＋CG2，则2AC2＝2AG2＋2CG2＝AE2＋AD2，

即AE2＋AD2＝2AC2.

教师继续启发引导学生质疑，用类比的思想去思考：在30°的直角三角形或一般的直角三角形中，斜边上的动点到直角三角形的三个顶点形成的三条线段是否也存在等式关系？从而产生如下的两个问题：

问题1：如图14，在△ABC 中，∠ACB＝90°，∠A＝30°，点P 是斜边AB 上的一动点.求证：4PC2=PA2+3PB2.

问题2：如图15，在△ABC 中，∠ACB＝90°，点P 是斜边AB 上的一动点.求证：PC2=sin2A∙PA2+sin2B∙PB2.

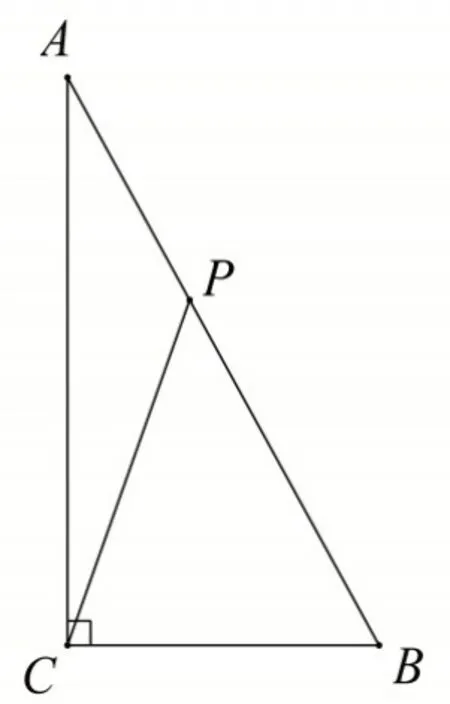
图14

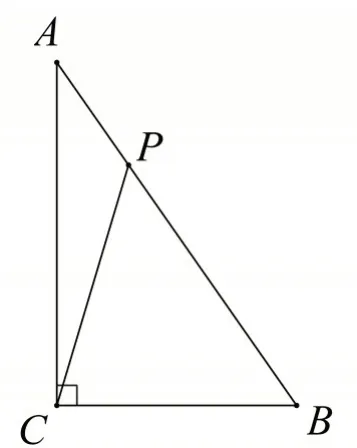
图15

在解题教学中，教师要善于引导学生质疑，变被动思维为主动思维，通过问题的探究变式，追根溯源，深化其对问题的认识，培养思维的批判性与深刻性.同时加强元认知训练，指导学生自己思维的过程再认识，形成反思自己思考过程的习惯，达到培养高阶思维的目的.