我国股票收益率分布特征的统计分析
张泽亚

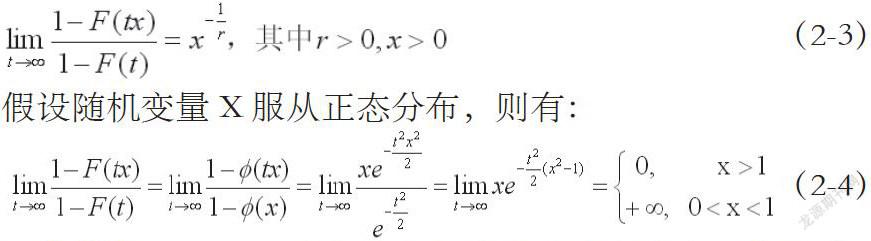



摘要:随着经济全球化以及投资自由化的发展,人们逐渐有了投资的意识,金融市场也越来越被需要。作为国民经济的晴雨表,股票关系到许多方面。因此,无论是对于政府主管部门还是广大股民,对股票收益率的分析都具有重大意义。除此之外,由于正態分布具备许多特殊的统计性质,所以人们常常将收益率假设为服从正态分布。然而近年来通过不断的研究发现,收益率通常具有“尖峰厚尾性”,这就意味着拒绝了其服从正态分布的传统假设。因此,分析收益率的分布特征不仅对研究收益率自身极为必要,而且对于其他的理论研究也具有重大意义。文章主要通过四个部分来进行介绍:首先是绪论部分,即介绍研究的背景、现状及研究意义。其次是正文部分,即对股票收益率进行正态分布检验以及尖峰后尾性质的检验,分析几种常用于解释收益率分布特征的分布,例举出几种检验拟合优度的方法,接着运用origin软件对几种中国股票收益率的实证分析研究,通过比较拟合优度找到适合解释收益率的统计分布。最后进行总结。
关键词:股票收益率;统计分析
1.引言
1.1研究背景
股份公司为了筹集资金,会发行给各股东一种有价证券,并以此作为持股凭证来获得股息和红利,这种有价证券被称为股票。股票最先起源于资本主义国家。1602年,在荷兰的阿姆斯特丹成立的东印度公司是世界上第一个股份有限公司。紧接着,英国和美国的股票市场也开始发展起来。我国最早出现的股票是外商股票。1986年,上海静安证券业务部的开张标志着中国第一个股票交易所的成立。在三十多年的发展中,中国股票市场经历了多变的政策选择,在不断的摸索中逐渐形成了完善的体系。
伴随着股票市场的发展,对股票市场的研究也从未间断。1990年,法国金融学家Louis Bachelier发表的一篇论文中第一次提出了用正态分布去拟合资产价格的分布。再后来,很多学者通过多方面的分析及证明也肯定了股票收益率服从正态分布这一理论。然而,在实际的股市行情中,股票收益率分布与正态分布的拟合程度并没有这么理想。一开始,人们会将无法拟合的点当作极端值或异常值。再经过很长一段时间的研究之后,许多科学家又开始尝试运用其他的方式来解释股票收益率的分布。近年来,在中西方学者的研究成果中都能够发现,股票的收益率并不是服从于正态分布,而是在峰值处较尖,峰度较陡,而尾处平缓呈现出了一种尖峰厚尾的特性,但是仍没有研究出一种可以准确拟合收益率分布的统计模型。
1.2研究意义
作为整个国民经济的基石,股市的作用和地位是不能被替代的。股票既可以通过充分调动社会中的闲散资金发展国家经济建设,还可以促进资金和经济的联系。因此,无论是对于政府、证券交易所还是对广大股民来说,正确地描述股票收益率的大致模型都具有重要的意义。分析出收益率的分布特征不仅有助于研究收益率自身分布的客观规律,也有利于研究其他相关的理论学说。
2.研究股票收益率分布的相关理论介绍
2.1股票收益率的定义及计算方法
股票收益率(即获利率)=股息或红利/股票市场价格。股票收益率可用于计算已得的和预测未来的股票收益率。计算方式如下:
假设Pt为t期末的股票价格,则从t期到t+δ期的股票差可以定义为:△Pt=Pt+δ-Pt。设Rt为简单收益率,则股票简单收益率为
若采用复利计算投资收益率,那么设Rt为年利率,n为每期复利的次数,δ为投资期限,当n→∞时,δ年后可获得的资金Pt+δ为Pt+δ=Pt·eδRt。
2.2正态分布及尖峰厚尾的定义
2.2.1正态分布的定义及图形特点
如果随机变量X的概率密度为:
则称X服从正态分布,随机变量X的均值为μ,标准差为σ,记为X~N(u,σ2)。当σ越小时,概率密度曲线f(x)的坡度越陡;当σ越大时,曲线f(x)的坡度越平。
2.2.2尖峰后尾的定义
尖峰厚尾分布的特性一般是相对于正态分布来说的。当离散程度(即方差)与正态分布相同时,在其均值位置处,尖峰厚尾分布的峰值较大,峰度较陡,峰处较尖,因此被称为尖峰分布。由于峰值处的集中水平较高,尾部相比较正态分布而言就会显得比较平坦,因此被称为厚尾分布。金融数据常常会出现尖峰厚尾的特征。
2.3正态性于尖峰后尾检验法
2.3.1Q-Q图检验
Q-Q图是一种散点图,可以通过观察来判断一组数据服从于哪一种分布,通常被用作检验是否服从正态分布。通常情况下,Q-Q图的横坐标为标准正态分布的分位点,纵坐标为实际的数值。当Q-Q图上的样本点近似地可以看作在一条直线附近时,就可以判断出该组样本数据近似服从正态分布,同时,这组数据的均值和标准差可以由该直线的截距和斜率得出。样本的偏态程度和峰态程度也可以通过Q-Q图粗略的得出。
2.3.2峰度检验
峰度,又被称为峰态系数。它测量了一组数据的分布平峰或者尖峰的程度。峰态系数作为测度峰态的统计量,一般由K表示。定义上,峰度系数相当于标准化数据的四阶原点距,四阶标准矩又可定义为:μ4/σ4,其中,σ为标准差,μ4为四阶原点距。一般情况下,当K=3时为正态分布;K<3时为扁平分布;K>3时为尖峰分布。
2.3.3偏度检验
偏度,又称偏态系数,用于测度数据分布的对称性,记作SK。偏度为一组数据的标准化三阶矩,定义式为E[((X-μ)/σ)3]=K3/σ3。由于正态分布的奇数阶原点矩均为零,因此正态分布的偏度系数为零。当SK<0时,可以判断出数据右偏;当SK>0时,可以判断出数据左偏。
2.3.4Jarque-Bera检验
Jarque-Bera统计量,简称JB统计量,它结合了偏度系数和峰度系数,用来检验样本是否服从正态分布。JB统计量的计算方法为JB=n(S2+K2/4)/6,其中,K为峰度系数,S为偏度系数。由于JB统计量服从自由度为2的x2分布,所以可以通过计算JB的值,分析随机变量的峰度分布情况:当JB<x2α(2)时,随机变量服从正态分布;当JB>x2α(2)时,随机变量不服从正态分布。
2.3.5厚尾分布检验
假设存在一组随机变量X,其分布函数F(X)满足
假设随机变量X服从正态分布,则有:
通常情况下,正态分布被人们认为是薄尾分布。因此由式(2-12)可得,当r>0时,随机变量可被视为厚尾分布;当r=0时,随机变量可被视为薄尾分布。
在过去的研究中,人们也尝试了运用多种统计模型去拟合收益率的分布情况。由于在接下来的章节中会用origin软件去拟合分布,所以在下一节中主要介绍origin软件中所包含的可以用来拟合收益率分布的几种分布模型。
2.4常用于解释收益率分布的统计分布
2.4.1柯西分布
柯西分布,在物理学中又被称为洛伦兹分布,其分布函数为:
其中,x0表示分布峰值所在的位置,γ为最大值一半处的宽度。当x0=0,γ=1时,称为标准柯西分布。柯西分布的概率密度函数图像为钟型,这一点与正态分布非常相似,但是柯西分布概率密度图下降至零的速度比正态分布慢了很多。
假设一组数据服从标准柯西分布,判断其是否具有厚尾特征:
从式(2-6)中可以得出r=1>0,因此在一定的条件下,柯西分布是一个厚尾分布。
2.4.2极值分布
在概率论中,对于某一特定的研究主体,按一定的特征将其划分成若干组,从每一组挑选出其中的最大值(或最小值),这些最大值(或最小值)会服从一定的分布f(x),f(x)就称为极值分布。在金融研究方面,极值分布常被用于对随即变量最大或最小值的概率分布和边际概率的尾部建立数学模型,预计所有持有资产的收益和预计风险。
在实际的运用中,为了方便,人们常用广义极值分布来表示极值分布,这时就会引入位置、尺度和形状参数,分别为μ,σ,ξ。在引入位置和尺度参数后,分布函数中的x就由(x-μ)/σ替代,接着引入形状参数,得到的统一的表达式为:
2.5拟合优度检验方法
2.5.1判定系数检验
判定系数是用于度量估计的回归方程的拟合优度。因变量y会受到自变量x以及除x以外其他因素的影响从而有所波动,这种波动称为变差。对于一个具体的数值来说,变差为观测值与这组数据平均值的差。总平方和就是n个数值变差的和,记为
则反映的是实际值与估计值的差,不能通过回归直线来解释,被称为残差平方和,用SSE来表示。通过分析可知,拟合程度的高低是由SSR和SSE来决定的,因此产生了判定系数R2。判定系数为回归平方和与总平方和之比:
实际数值如果与估计值越接近,则SSE就越小,R2就越大;当R2=1时,实际数值与估计值完全拟合;若SSE越大,则说明实际数值越远离估计值,R2就会越小。因此,可以通过R2的值来判断拟合优度:R2越大,拟合程度越好;R2=1时,完全拟合。
2.5.2残差图检验
残差通常用e表示,写为 ,表示实际观测值与回归后的估计值之间的差值,一组数据中所有的残差相加就为残差平方和SSR。
由于在回归模型中存在一个假定期望等于零、方差相等且服从正态分布的随机变量ε,因此对回归程度的检验也可以说是对随机变量ε的假定是否成立的检验,这种检验的方法之一就是运用残差图分析。若回归模型选取合理,那么残差分布图中的所有点都应该分布在一跳水平区间之中。如果残差图中的点分布在一条逐渐扩大的区间内或者散乱分布,表明所选取的拟合模型是不合理的,需要考虑更换模型重新拟合。
3.中国股票收益率分布特征的实证分析
3.1数据选取
为了验证我国股票收益率的分布情况,本章节选取了上证指数和深证A指从2013年至2019年股票收益率的数据,来研究其分布特征。
上证指数,即上海证券综合指数,1991年7月15日正式发布,反映的是在上海證券交易所所上市的全部证券股票价格的实际变动情况。深证成份股指数是从上市的所有股市中抽取40家有代表性的公司,将他们的股市作为分析对象,并把权数设定为流通股,计算得出加权股价指数。
3.2收益率的正态性和尖峰后尾检验
在以前的大部分文献中,收益率是服从正态分布的。但是近几年经过人们的反复分析,有一部分人则认为收益率具有尖峰后尾性,因此并不服从于正态分布。利用SPSS做QQ图后可以发现,虽然收益率大部分呈一条直线,但是尾处与直线偏离程度较大,因此分析收益率为厚尾分布。通过计算可得,上证指数的偏度和峰度分别为-0.942和6.487,深证A指的偏度和峰度分别为-0.827和3.722。
假设置信区间为95%,提出假设H0:收益率服从正态分布;H1:收益率不服从正态分布。由上两表的数据可以得出可用来判断是否服从正态分布的JB值:
查表得xα(2)=5,上证指数与深证A指的JB值明显大于5.991,所以拒绝原假设,上证指数与深证A指的收益率不服从正态分布,而是具有尖峰厚尾的特性。
3.3收益率分布模型的拟合
由第二章的内容可知,在origin软件中,柯西分布和极值分布在一定的条件下可能可以比正态分布更好地拟合收益率分布情况,因此需要判断出哪一个统计模型可以更好地用来描述收益率分布特征。
在进行分析之前,由于每一个数据都具有自己的维度,即一个数据会受到多方面的影响。如果直接采用原始数据进行分析,那么这些方面对股票收益率的影响程度是不一样的,因此需要对数据进行标准化处理。使数据标准化的方法有很多,这里采用正规化方法,即z-score标准化对数据进行变化。
在得到一组标准化的数据后,作出这组数据的频数分布表,在图中连接各点后与上述统计模型拟合,拟合得出的结果如下:
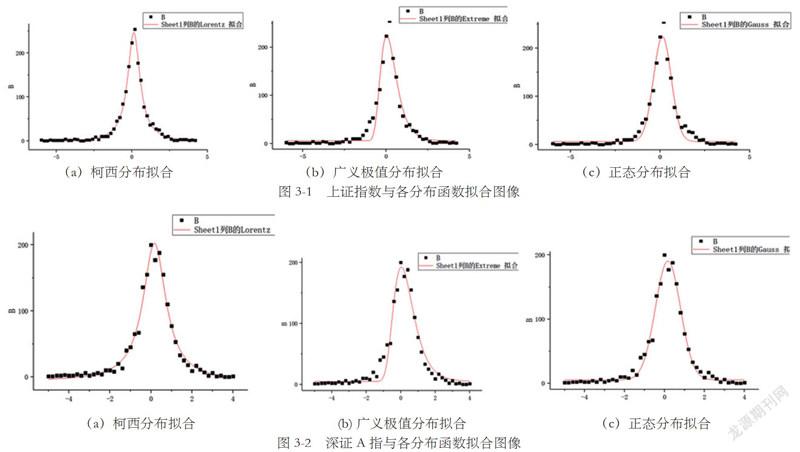
图3-1中的四张图显示了用origin软件拟合上证指数与柯西分布、广义极值分布以及正态分布拟合的大致图像。从图中可以看出,广义极值分布则不能较好地拟合收益率的峰度和左尾。从拟合的图像上可以判断在这三种分布模型中柯西分布用来描述上证指数收益率是最优的。下面继续分析这三种模型与深证A指的拟合程度。
图3-2显示了三种分布模型与深证A指收益率分布的拟合情况。由上图可以看出,广义极值分布仍不能较好地拟合收益率分布的左尾;然而在拟合深证A指时,正态分布与柯西分布的拟合程度都较好。接下来需要通过拟合优度的计算以及残差图来判断哪种模型能够最好的拟合收益率分布。
3.4拟合优度的检验
根据第二章节的内容得出,可以通过残差图以及判定系数来比较拟合优度。但是当做出残差图后发现,各个分布拟合后除个别极端值外,基本上都落在了一条水平带中间。
通过origin软件可求得各拟合的判定系数,其中上证指数的柯西分布、广义极值分布、正态分布的分别为0.99378、0.94846、0.96963,深证A指的柯西分布、广义极值分布、正态分布的分别为0.98282、0.95484、0.98275。所以,不论是上证指数还是深证A指,柯西分布拟合后的判定系数都大于其他分布拟合后所得的判定系数,再结合之前的残差图可以得出以下结论:柯西分布较正态分布和广义极值分布相比可以更好地拟合股票收益率分布。
4.总结与展望
4.1总结
本文主要研究的是通过统计的方法对中国股票收益率分布特征进行分析。首先介绍可以运用于解释许多分布情况的正态分布模型去拟合。显然,正态分布不能够很好地反映收益率分布的峰度和尾部分布情况,从而证明收益率不是完全服从于正态分布的。股票收益率属于金融数据,易受到时间的影响,而且极端值出现的概率较大。通过峰度的计算及检验,得出我国股票收益率服从尖峰厚尾分布。本文中的第二章节介绍了origin软件中一些可以用来拟合收益率分布的几种统计模型以及拟合优度的检验方法,例如柯西分布、广义极值分布等。接着,对我国2013-2019年的上证指数和深证A指进行了实证分析,并通过拟合优度检验发现,柯西分布能够比正态分布更好地解释收益率分布的峰度和尾部,所以说柯西分布也可以较好地拟合我国收益率的分布情况。
4.2展望
金融市場的数据分析一直是一个热门的话题。尤其是股票收益率,吸引了很多学者的关注。近代的学者们已经推翻了以前人们所得出的收益率服从正态分布这一论点,得出了收益率有尖峰厚尾的特性,并分析出了收益率可以近似地由混合正态分布或t分布去拟合,取得了很大的进步。但是,股票收益率是一个复杂的系统,受着很多因素的影响,目前所研究出的拟合模型其实也不能完全用来去解释收益率的分布情况。在以后的分析和研究中,学者们也会将这些影响因素带入分析的范围内,研究出更好地可以拟合收益率的统计模型。通过统计模型的建立去预测将来股票收益率的发展情况,为人们的投资指明更好的道路。
参考文献:
[1]余之明.股票的起源及发展探微[J].中国机电工业,1999(1):37-38.
[2]边宽江,程波,王蕾蕾.收益分布尖峰厚尾问题的统计检验[J].统计与决策,2009(7):83-85.
[3]朱松涛.关于Cauchy分布的若干结论[N].济宁师范专科学校学报,1995(3):5-7.

