大跨径上承式钢管混凝土拱桥非线性稳定分析

孙明书 李丰 郭小坤 张森华

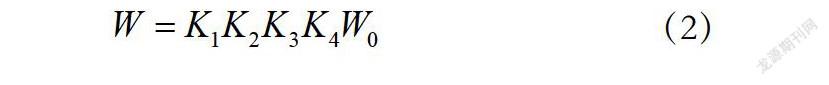
摘 要：钢管混凝土拱橋以钢管和内填混凝土材料协同受力，在充分满足结构抗压强度的同时大大节省了混凝土材料的使用。由于其施工方便，施工时间短，能够极大程度上提高了桥梁的跨越能力，因此在山区桥梁结构中的得到广泛推广。但是随着大跨度钢管混凝土的跨径不断增大，拱桥稳定性问题显得尤为突出。结构一旦稳定性不足，发生失稳破坏，拱桥结构会在没有征兆下发生整体垮塌，极大的影响了交通的正常使用，重则对影响人生安全，对社会造成不可估量的社会影响和经济损失。本文通过对一座跨径为300 m的上承式钢管混凝土拱桥建立Midas有限元模型，并通过不同倍数模态偏位作为结构初始几何缺陷施加到模型结构中，考虑由于拱肋初始挠度缺陷导致的桥梁结构变化，对该模型进行特征值屈曲分析，进行桥梁非线性稳定分析。结果表明，考虑几何缺陷的非线性对该上承式拱桥稳定性有较大影响，主要表现为稳定性系数随施加的初始缺陷值增加而衰减，因此上承式拱桥稳定性分析时考虑几何非线性才能真实模拟工程实际情况。

关键词：初始挠度缺陷;钢管混凝土拱;非线性;稳定性

中图分类号：U448.14 文献标识码：A

由于钢管混凝土拱桥具有施工方便、节省材料、极大程度提高桥梁跨越能力和承载力等优点，所以在山区桥梁结构中得到广泛推广，成为山区桥梁结构的首选桥梁形式。但是随着大跨度钢管混凝土的跨径不断增大，拱桥稳定性问题显得尤为突出。稳定性问题对于大跨度桥梁而言是极为重要的考虑因素，尤其是针对大跨度拱桥而言，结构一旦稳定性不足，发生失稳破坏，拱桥结构会在没有征兆下发生整体垮塌，极大的影响了交通的正常使用，重则对影响人生安全，对社会造成不可估量的社会影响和经济损失。因此本文以净跨径为300 m的贵州某钢管混凝土拱桥作为工程实例，钢管混凝土拱桥在制造、安装等施工过程中易造成拱肋发生局部变形，因而影响主拱圈线性成桥后的拱轴线，当主拱圈拱轴线与原设计拱轴线不一致时，则会使得拱肋产生初始挠度，进而影响桥梁的承载力与使用寿命，这无疑大大影响桥梁结构的安全性与适用性。因此，针对有初始缺陷（初始挠度）的拱肋的稳定性分析，具有一定的科学研究意义与社会价值。

1 计算概述

1.1 空间非线性稳定分析

钢管混凝土拱桥继承了拱桥以受压弯为主的受力特点。拱在不同的结构和荷载情况下，丧失第一类稳定和第二类稳定都是有发生的可能性。所有材料都不可能无限弹性，在考虑实际问题中，假设材料为无限弹性是不现实的，所以不考虑第一类稳定情况。但是第二类失稳在拱桥结构中极为常见，即由于施工阶段的众多不确定性（施工预拱度的设置、施工线性误差、施工不对称加载等）造成的拱轴线偏位使得拱桥失稳。随着跨径的增大，拱桥第二类失稳主要呈现出大变形大应变的特点，其导致的后果也因此无法承担，因此，在拱桥结构的设计中，应充分考虑由于材料非线性和几何非线性导致的失稳尤为重要。由于钢管混凝土拱肋与石板拱、钢筋混凝土板拱肋等形式相比，其受力特点较为接近钢拱桥，由此其稳定性分析显得更加必不可少。同时钢管和混凝土进入塑性阶段应力应变关系的线性，故本文针对大位移小应变情况下的钢管混凝土拱肋进行了其受力和变形情况的分析。采用全量方法求解，拱桥结构非线性平衡方程式[6]见式（1）。

式中：

另外，和是的函数，因此式（1）为非线性方程组。

现有的非线性方程组求解主要有逐步的迭代法、直接迭代法、荷载增量法等，但是在工程实际中主要采用荷载增量法进行分线性方程组求解。其主要思想为：当荷载从0逐渐增大到时分别逐步求解方程。当发散时，定义为拱桥的极限承载能力，一般可以通过Euler—Cauchy法、半增量法等求解，其本质为采用一系列线弹性解逼近结构非线性解。

1.2 组合材料的本构关系

钢管混凝土拱桥主要是以钢管和内填混凝土材料协同受力，在充分满足结构抗压强度的同时大大节省了混凝土材料的使用。

其中，钢材料一般按照钢结构中规定的本构关系作为设计标准，即采用刚塑性本构关系[1]。由于规范中规定的结构失稳破坏必须在强度破坏之后发生原则，在不考虑荷载分项系数的前提下，根据边缘纤维屈服准则分析发现结构容许应力安全系数不应小于整体稳定安全系数，工程实际中钢结构的稳定性系数不小于1.7。

在已有的混凝土本构关系[2]中，一般将其极限应变取为0.003 5。

2 非线性稳定分析

2.1 工程实例

本文采用的工程实例为贵州某座上承式钢管混凝土拱桥（主跨为300 m，净矢高为54.545 m，矢跨比为1/5.5），该桥选用拱轴系数为1.543的悬链线作为理想拱轴线。

该桥选用等宽度变高度作为主拱圈截面，变截面的高度5 m～9 m之间成拱顶至拱脚变化，其拱肋之间用过横联合米撑联系，主要结构（上弦拱肋、下弦拱肋）均采用等截面钢管，但不同部位采用不同钢管厚度，主要管径变化区间为（Φ1 200x26 mm～Φ1 200x35 mm）。钢管与拱肋连接方式采用标准内法兰盘接进行内接，管外连接方式选用为焊接的方式。混凝土材料选用C55自密实微膨胀混凝土。

本桥依据节段运输长度限制和吊装重量控制作为本桥施工时划分主拱圈节段的依据，本桥全跨（330 m）共划分为13 个节段。大桥总体布置、主梁截面布置图、拱顶立面图如图1所示。

2.2 结构初始几何缺陷考虑

钢管混凝土拱桥在制造、安装等施工过程中易造成拱肋发生局部变形，因而影响主拱圈线性成桥后的拱轴线，一旦设计理想拱轴线发生变化，则会使得拱肋产生初始挠度。由于钢管混凝土拱桥施工阶段不可避免的施工误差，所以初始缺陷必定存在。初始挠度缺陷不能确定其位置，具有一定的随机性，因此在屈曲分析之前先进行一个特征值分析。

（1）由于特征值屈曲载荷一般表示为理想设计拱轴线下的线性屈曲载荷的上限，因此将该指标作为给定载荷代入计算模型中进行非线性分析，正常条件下，在逐步加载至屈曲载荷上限时该模型求解结果显示为发散。

（2）求解模型求得的特征值矢量屈曲形状与实际状态下的屈曲模态分析是最为接近的，因此将特征值矢量屈曲形状作为判断模型中施加初始缺陷的基本依据。

2.3 初始缺陷下稳定性分析

本桥采用Midas有限元软件进行分析计算，建好模型之后，添加荷载工况并施加荷载。由于拱桥的u影响显著，故将风荷载定义为用户自定义荷载。风荷载是一种流体作用于桥上，受力情况复杂，现有《公路桥涵通用规范》中规定风荷载的计算方式。本文中风荷载作者考虑选取风的静力作用，计算横桥向风力。横桥向风压计算公式见式（2）。

式中：

定义屈曲分析数据，一般荷载的频率是比较低的，所以我们只需考虑前几阶（低阶）模态，在这模态数量作者选取了前5阶。将自重和风荷载添加到屈曲分析控制数据里面，运行屈曲分析。从分析结果表格中找到设置的前5阶模态。

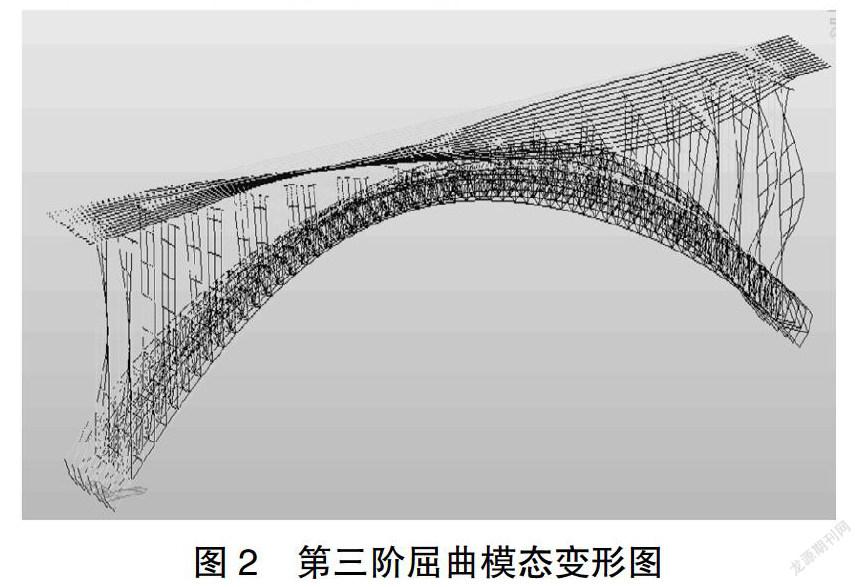
针对该模型进行特征值屈曲分析结果，提取模型前五阶模态[5]进行分析比较发现，前五阶屈曲模態均主要发生面外失稳，由此证明与面内刚度相比，本桥结构面外刚度相对较小。因此，本文采用了一、二、三阶面内变形为主模态施加初始挠度缺陷，模态图如图2所示。

以第一阶模态施加不同倍数的模态偏位形式作为结构的初始几何缺陷，求得稳定系数做说明。在结果分析中查看第一阶屈曲模态图中屈曲向量中最大值，也可将结果导入Excel表中进行排序分析。再按照规范计算施加初始缺陷的最大值，将计算除的所需施加的初始缺陷的最大值与屈曲向量中的最大值相比，所得的比值保留。将所有屈曲向量均乘以这个比值，即可得到各个节点的初始缺陷值。再把各个节点坐标加上各个节点的初始缺陷值，改变各个节点的坐标，就完成添加初始缺陷这一步骤。

添加完初始缺陷之后进行非线性屈曲分析。在荷载组合里先自动生成荷载组合，建立或修改需要的非线性荷载工况进行荷载组合。在非线性荷载组合下，结果查询数据里线弹性分析下位移最大的点，做为非线性分析的控制点。最后设置非线性控制数据，查看荷载—位移曲线，即步骤时程图表中可以直观的看到稳定系数。

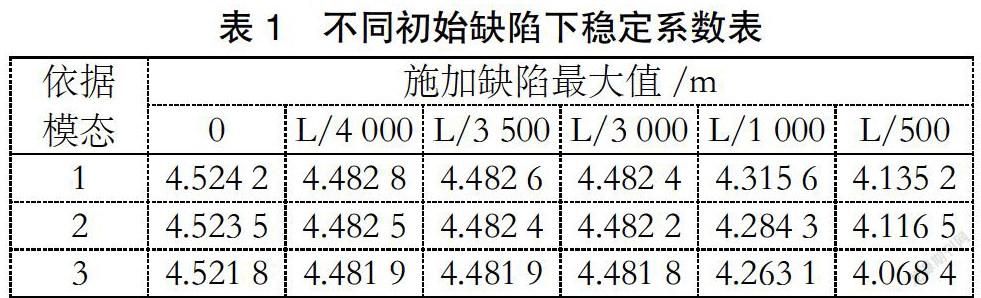
大致上来说，就是以特征值屈曲分析下第一、二、三阶模态变形为基础，施加不同倍数的模态偏位形式，作为结构的初始几何缺陷。通过有限元软件分析，进而得到不同初始几何缺陷下的稳定系数，见表1。

根据表中数据可以得到以下结论：

①在施加的模态偏位形式为相同类型的的条件下，该桥结构稳定性系数随着初始几何缺陷数值的不断增加而逐渐减小。

②当模型的施加位移模态形式不同时，随着施加的缺陷最大值不断增大，其对应的稳定系数间在、差距逐渐扩大。

③该模型各位移模态的极限承载力的最大缺陷值在规范[4]规定区间（L/4000～L/3000）时，其稳定系数变化相对很小。

3 结语

本文通过对贵州某座上承式钢管混凝土拱桥有限元仿真模拟，分析了添加初始缺陷后的该桥几何非线性稳定情况，得到如下结论：

（1）通过添加几何初始缺陷，桥梁的稳定系数有明显地下降，随着初始缺陷数值的增加而逐渐地减小。

（2）数据分析表明，最大初始缺陷值该模型中取为L/4000～L/3000之间时，其结构稳定系数变化相对稳定。这一结果恰巧满足《公路桥涵施工技术规范》中规定的钢管混凝土拱肋线形的安装允许偏差（侧向应小于等于L/4000，竖向应小于等于L/3000）。

（3）几何非线性对大跨度上承式钢管混凝土拱桥稳定影响很大，因此上承式拱桥稳定性分析时考虑几何非线性才能真实模拟工程实际情况。

（4）本文中只考虑了自重和风荷载情况下添加几何初始缺陷的非线性稳定情况，对于大跨径钢管混凝土拱桥中温度变化等荷载工况也会对其稳定性产生影响，因此还需后面的研究讨论。

参考文献：

[1]韩林海，陶忠，杨有福，等.新型钢管混凝土结构的力学性能与设计理论研究第十三届全国结构工程学术会议特邀报告[J].工程力学，2004，21（S1）：60-89.

[2]曾勇，马如进，陈艾荣.大跨度上承式钢管混凝土拱桥的非线性稳定分析[J].上海公路，2028，27（02）：50-53+5-6.

[3]张建民，郑皆连，秦荣.南宁永和大桥双重非线性稳定分析[J].公路交通科技，2002，19（03）：58-62.

[4]路桥集团第一公路工程局.公路桥涵施工技术规范[M].人民交通出版社，2000.

[5]信丽华，林玉森，段树金.初始几何缺陷对钢管混凝土拱桥极限承载力的影响[J].石家庄铁道大学学报（自然科学版），2009，22（03）：10-13.

[6]李国豪.桥梁结构稳定与振动[M].中国铁道出版社，1992.

[7]赵河清，徐亮，杨惠林，等.大跨度上承式钢管混凝土拱桥的稳定性分析[J].公路交通科技，2006，23（11）：82-85.

[8]陈宝春.钢管混凝土拱桥设计与施工[M].人民交通出版社，1999.