MATLAB在概率论教学中的实践
任建国 刘小锋

摘要:概率论这门课程是研究随机现象数量规律的学科,在经济管理、自然科学、工程技术等众多领域应用相当广泛。且其相对抽象,逻辑性较强,对于经管类专业的学生来说,有一定的难度。若将MATLAB引入概率论的课堂,可以将抽象的知识形象化,将复杂的知识简单化。同时激发学生的创造性思维,使其成为学习的主题,调动学生的兴趣。
关键词:概率论;教学改革;学习兴趣;MATLAB
1引言
概率论是高等学校经管类专业的一门基础必修课程,与高等数学和线性代数相比,有其自身的特点。概率论的基础是微积分和线性代数,同时它又是统计学和计量经济学等后续课程的基础,其主要是研究随机现象数量规律的学科,在经济管理、自然科学、工程技术等众多领域应用相当广泛。我们的目标是通过学习,使学生能掌握随机现象的思想和方法,这对于经管类专业的学生来说,有一定的难度,为了提高教学效果以及学生的学习兴趣,有必要引入MATLAB进入概率论的课堂,将很多概念和性质图片化、形象化,也可以将很多繁琐的习题通过MATLAB快速的将其结果实现,这样学生理解起来更直观,同时在学习的过程中又无形的提高了学生的实践操作的能力。
2应用举例
2.1利用MATLAB讲解二项分布的正态分布近似
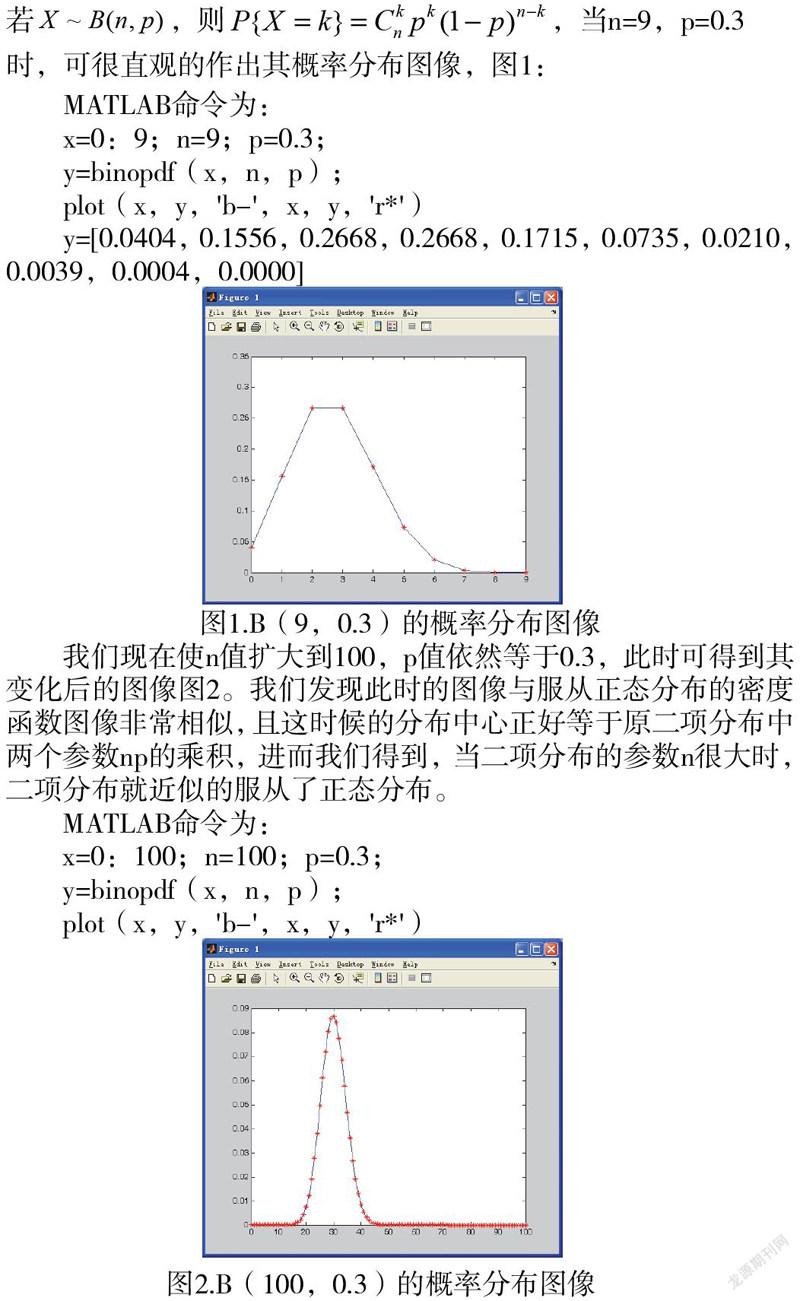
若,则,当n=9,p=0.3时,可很直观的作出其概率分布图像,图1:
我们现在使n值扩大到100,p值依然等于0.3,此时可得到其变化后的图像图2。我们发现此时的图像与服从正态分布的密度函数图像非常相似,且这时候的分布中心正好等于原二项分布中两个参数np的乘积,进而我们得到,当二项分布的参数n很大时,二项分布就近似的服从了正态分布。
可从课程名称《线性代数》出发,问学生代数是什么意思,线性是什么意思。着重介绍下代数的历史与框架,把学生中小学学过的代数知识串联起来,使学生对代数的历史有个整体的了解。代数的字面意思为用字母代替数,它的主要任务是解方程。我们可以从最简单的一元一次方程开始,从元和次两方面展开,从古代巴比伦一直讲到费马大定理及哥德巴赫猜想,让学生感受到代数的内在美。
2.2利用MATLAB讨论二项分布、泊松分布和分布函数的关系
(1)对二项分布,画出的分布律点和折线;
(2)对,画出泊松分布的分布律点和折线;
(3)对,画出正态分布的密度函数曲线;
(4)调整,观察折线与曲线的变化趋势。
我们可以得到下面的图3.
我们发现,在二项分布中,当n值很大,p值很小,且np的乘积比较适中的时候,可以用泊松分布来近似二项分布;当n值很大,而p值并不是很小且np乘积并不适中的时候,二项分布的图像近似于正态分布的图像。
3小结
将MATLAB与概率论这门课相结合,可以使抽象的概念和性质形象好,将比较复杂的习题简单化,可以激发学生的学习兴趣,由被动变为以学生为主体,调动学生的积极性,同时能够让学生发现数学中的美,做到教学相长,起到事半功倍的效果。
参考文献:
[1]茆诗松,程依明,濮晓龙.概率论与数理统计[M].第2版.北京:高等教育出版社,2011..
[2]张崇岐,李光辉.统计方法与实验[M].北京:高等教育出版社,2015.
[3]刘卫国.MATLAB程序设计教程:第2版[M].北京:水利水电出版社,2010.
[4]李尚志.线性代数教学改革漫谈[J].教育与现代化,2004(1):3-6.
作者简介:任建国(1981.4-),男,汉族,河北省邯郸市,硕士,上海财经大学浙江學院,公共基础部,讲师,研究方向:应用数学。
通讯作者:刘小锋(1981.9-),女,汉族,河北张家口人,硕士,上海财经大学浙江学院,公共基础部,讲师,研究方向:社会统计与调查、数理统计。
(上海财经大学浙江学院 公共基础部 浙江金华 321013)

