基于随机森林的点蚀电位预测

邢易　李树枝

摘要：点蚀是不锈钢点焊接头最常见的失效形式之一。点蚀电位作为衡量点蚀行为的特征量，与焊接电流、焊接时间、电极压力等参数有着复杂的非线性关系。针对文献中不锈钢接头点蚀行为数据，建立随机森林模型，优化的决策树数目为1 000，通过“五折交叉验证”确定节点备选变量个数为2。预测结果表明：除29号样本预测相对误差较高外（-14.81%），剩余样本的预测结果均优于神经网络和支持向量机，相对误差的绝对值在10%以下。

关键词：点蚀电位;随机森林;交叉验证;非线性

中图分类号：TP181文献标志码：A文章编号：1001-2303（2020）05-0045-05

DOI：10.7512/j.issn.1001-2303.2020.05.09

0 前言

电阻点焊以其高效、低应力、小变形以及良好的自动化适应性等优势，广泛应用于汽车、铁路、航空、电子等工业领域中，可实现低碳钢、不锈钢、铝合金、高温合金的焊接。

不锈钢具有优良的机械性能和耐蚀性能，但在点焊过程中其接头性能受到较大影响，尤其是耐蚀性。点蚀是一种局部腐蚀现象，点蚀电位作为点焊接头点蚀行为的评价依据，可通过焊接时间、焊接电流等[1-3]焊接参数实现预测和评价。

随机森林是Breiman L.[4]在2001年提出的机器学习算法。该算法以决策树作为基学习器，采用并行化思想，实现模型的训练和预测。随机森林算法优点众多，非常适用于处理复杂、非线性问题，而且几乎不会出现过拟合，预测效果好，在农业、林业、生物医药、信息通讯等[5-9]众多领域中有着重要应用。李欣海[5]利用随机森林对昆虫种类进行判别;陈华舟[6]将随机森林回归与基尼系数优选变量方法结合，实现鱼粉蛋白的定量分析预测;Milad Malekipi-rbazari[9]利用随机森林模型进行社交借贷风险评估。而目前随机森林算法在材料学科中的应用研究还非常少见。

文中借助于R语言平台，利用randomForest[10]（随机森林）软件包对不锈钢的点蚀行为数据进行随机森林建模，通过模型参数选择、优化，实现模型训练、预测和评价过程。

1 随机森林模型

点蚀电位属于连续型变量，探究、预测其与焊接过程参数的关系属于典型的回归问题，可采用构造以决策树为基学习器的随机森林回归模型来分析和解决此问题。

1.1 随机森林训练

随机森林是一种集成学习算法，其采用自助抽样法，构造多棵决策树组合{h（x，βk），k=1，2...r}，x是输入向量，βk是独立同分布的随机变量，r是决策树的数量。随机森林训练过程包括以下步骤：

（1）采用随机抽样从原始数据中获得训练数据样本，并采用自助抽样法（bootstrap）从训练集样本中有放回抽样得到r个不同的集合，分别作为r个决策树的根节点样本集合，每次抽样剩余的数据作为袋外数据，用于模型误差的评估。

（2）对于任意一棵决策树，每次进行节点裂时从所有的特征中随机选取几个特征进行最优变量分割，并让决策树最大限度地生长。

（3）重复步骤（2），当所有决策树生长完毕，随机森林训练也随之完成。

1.2 随机森林预测

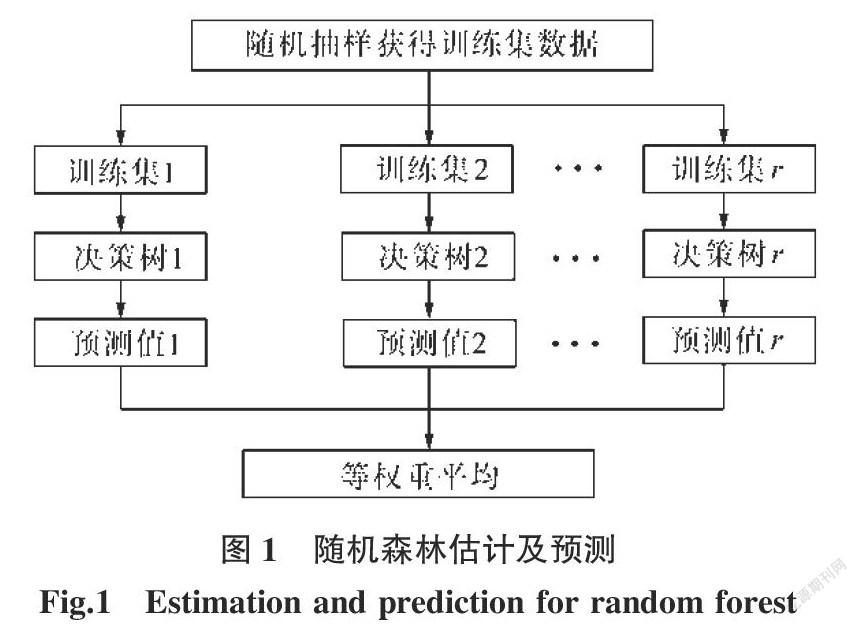
随机森林预测如图1所示。

（1）对一棵训练完成的决策树，当有样本输入时，相应变量根据节点划分从根节点沿着满足条件的划分路径走到末节点，末节点预测变量均值即为该决策树的预测结果。

（2）对所有的决策树重复上文中步骤（2），每棵决策树都会给出变量的预测结果，将这些结果进行等权重平均即可获得最终的预测值。

2 数据建模及评价方法

文献[10]中不锈钢焊接参数如表1所示。自变量为焊接时间（wt）、焊接电流平方（wc2）和电极压力（ef），E为点蚀电位。焊接过程是一个典型的非线性动力学过程，不同的参数组合产生不同的热循环，导致接头组织也不尽相同，进而影响接头的点蚀行为。随机森林适宜处理这类非线性作用过程的问题，在不显著提高计算量的前提下，获得比较理想的预测结果。

基于以上分析，建立以焊接时间、焊接电流平方和电极压力为输入变量，以点蚀电位作为输出变量的随机森林模型。随机抽取5/6的原始样本数据作为训练集，剩余样本数据作为测试集，实现模型参数的选择、模型分析和评价。

2.1 模型参数选择

根据随机森林算法估计过程可知，随机森林的主要参数有两个：决策树数目和节点备选变量个数。一般来说，决策树数目不应太少，否则会导致选取分割变量时，部分变量被选中次数过少，该因素对预测结果的贡献不能充分体现，导致预测结果发生较大偏差。节点备选变量个数则不应超过自变量个数。两个参数的确定方法如下：

（1）根据训练集样本进行模型训练，获得不同基学习器数目下训练集的均方误差，均方误差表征相对误差波动程度大小，计算方法如式（1）所示，根据其结果选择合适的决策树数目。

（2）针对训练集数据，进行“五折交叉验证”获得最佳的节点备选变量个数。即将数据随机均匀地分为5份，每次利用任意4份作为训练子集样本，剩余1份作为测试子集样本。变化节点备选变量个数，对模型进行训练和预测，得到模型训练子集和测试子集的平均均方误差大小，综合分析训练子集和测试子集误差结果，确定模型的节点备选变量个数。

2.2 变量重要性评价

使用精确度的平均减少（节点不纯度）来定量评价变量的重要性。评价方法包括：

（1）对训练好的随机森林模型，获得袋外数据预测结果的误差大小error。

（2）针对某一决策树的训练数据，为训练数据中某一变量i的变量值增加随机扰动，得到新的预测结果误差为error1，这棵决策树的变量i的精确度平均减少大小為error1-error。

（3）重复步骤（2），获得所有决策树的变量i的精确度平均减少值，取其平均值作为该变量在随机森林模型中的精确度平均减少值。

（4）重复步骤（2）、（3），获得所有变量的精确度平均减少值大小。

精确度平均减少数值越大，说明该变量添加随机扰动时，其对预测结果影响越大，即该变量的重要性越高;反之，变量的重要性较低。

2.3 模型结果评价

在上述选取的参数条件下，对测试集数据进行预测，获得预测值与实际值的相对误差大小，将结果与神经网络和支持向量机的预测结果进行对比、分析和评价。

3 结果分析及讨论

3.1 决策树数目选择

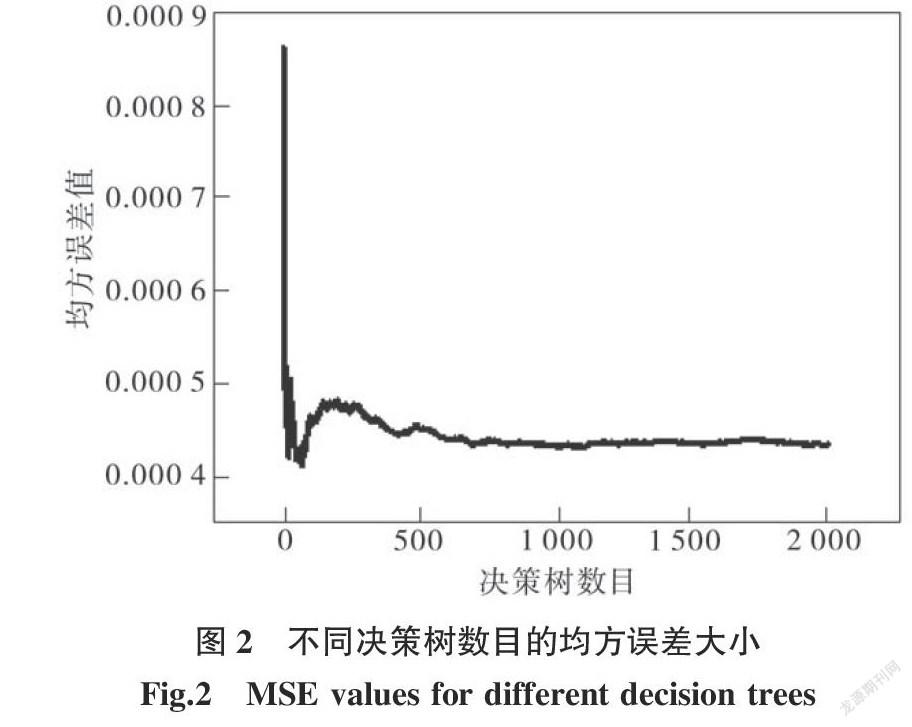
决策树数目在1～2 000范围内变化，获得训练模型的均方误差大小，结果如图2所示。决策树个数小于250时，误差在局部范围内出现几次较大波动，而后随决策树数目的增多，波动幅度逐渐减小。这主要是由于待分割的节点变量和训练样本是随机选取的，决策树数目很少时，这两方面的随机性导致误差出现较大波动;而随着决策树数目的增多，从总体来看分割变量的选择是均匀的，各个变量对预测变量的影响能得到全面的体现，波动幅度逐步降低。决策树数目大于250时，模型均方误差逐步减小，模型效果也越来越好，当决策树数目增大至1 000左右时，模型均方误差趋于最小;继续增大决策树数目，模型均方误差未得到更好的改善。因此，将决策树数目确定为1 000即可。

3.2 节点备选变量个数优化

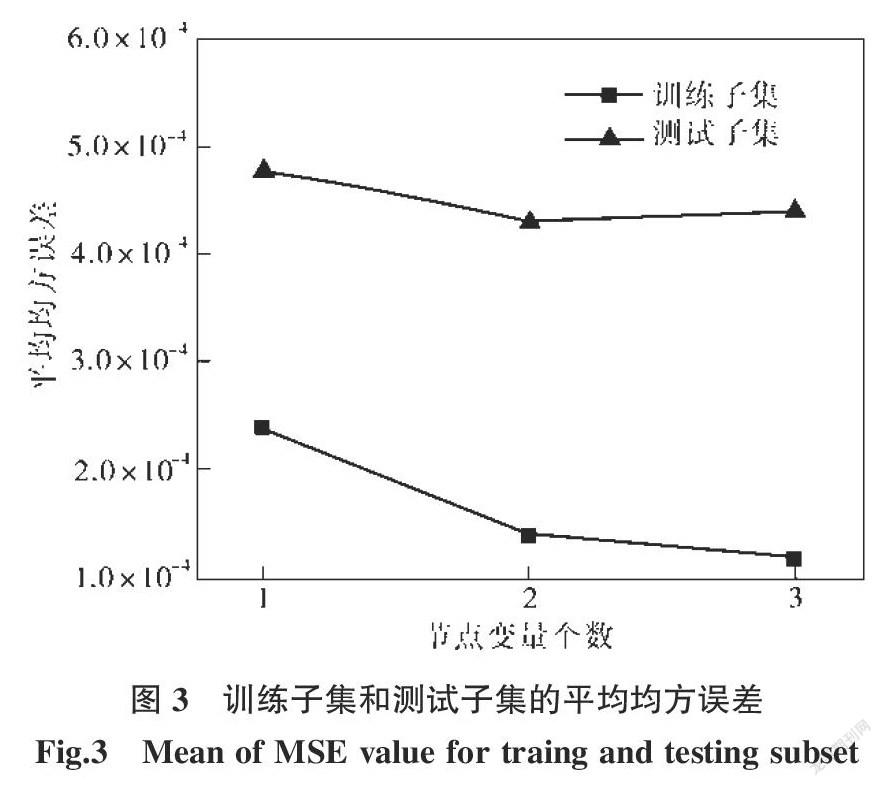
利用训练集样本对模型进行训练，使用五折交叉验证法得到训练子集和测试子集的平均均方误差值，结果如图3所示。训练子集和测试子集的平均均方误差值均在5e-4以内。说明真值与预测值间误差的波动程度小，拟合优度和推广优度均比较优异。在相同条件下，训练子集的平均均方误差均小于测试子集的平均均方误差，拟合优度结果优于推广优度。分析均方误差的变化规律可知：随着节点备选变量个数增多，训练子集的平均均方误差逐渐减小，变量个数为3时，平均均方误差达到最小值;而测试子集的平均均方误差先减小后增大，备选变量个数为2时误差达到最小，这两种条件下训练子集的平均均方误差相差不大，应优先选择测试子集均方误差较小者，即确定节点备选变量个数为2。

3.3 变量重要性分析

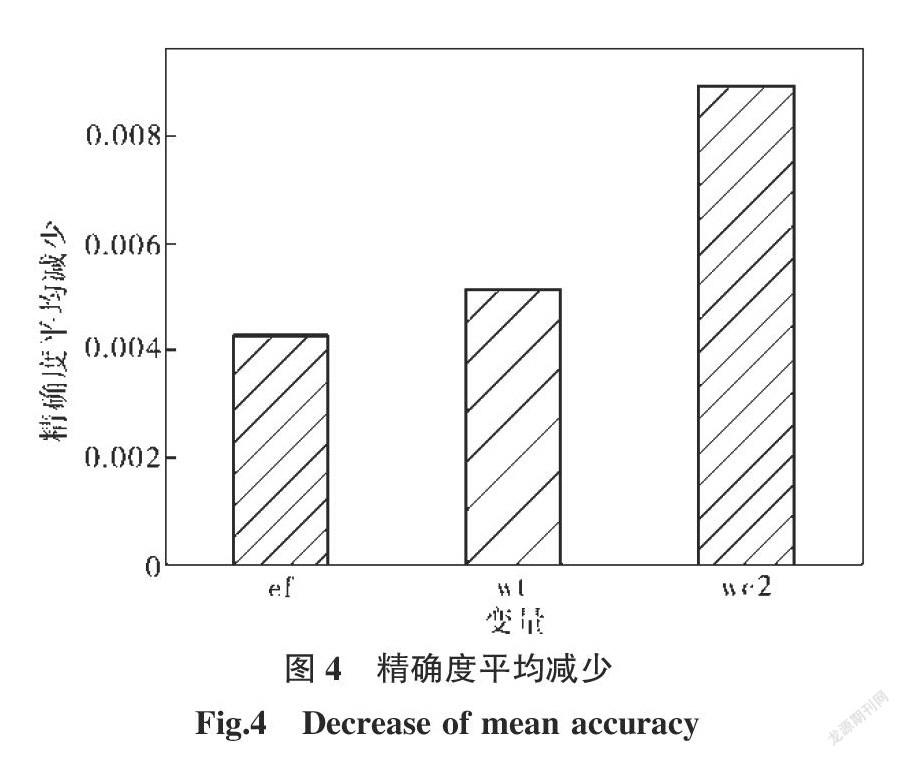
各个变量精确度的平均减少结果如图4所示，对点蚀电位影响最大的变量是焊接电流的平方值，其次是焊接时间，最小的是电极压力。焊接电流变化时，通过焊接电流平方被放大，接头热输入存在较大差异，造成接头组织差异明显，对点蚀行为产生较大影响，其重要性最高。同时，根据焦耳定律，焊接热输入变化对焊接电流的敏感度大于对焊接时间的敏感度，焊接时间对接头点蚀行为的影响小于焊接电流平方的影响。电极压力通过改变接触电阻间接影响热输入量及接头点蚀行为，但电极压力仅有两个独立的取值，变量的随机干扰对预测结果的影响小于前两个因素带来的影响，其精确度的平均减少最小，意味着该变量的重要性最低。

3.4 模型预测结果及评价

在备选节点变量个数为2、决策树数目为1 000条件下，利用模型对测试集样本数据进行预测，点蚀电位预测结果（pre）和相对误差大小（rel_error）如表2所示。可以看出，29号样本的预测相对误差为-14.81%，略微偏高。除29号样本外，预测值与真实值的相对误差的绝对值均在10%以内，绝大多数点的预测误差绝对值在5%以内。分析训练数据的点蚀电位可知，训练集自变量和预测变量的数据变化均比较均匀，预测变量的点蚀电位值在0.381 87～0.485 47 V范围内波动，训练集数据经模型训练后，对真实结果位于该范围内的样本预测效果会比较优良，而对于变量值偏離该范围较大的样本而言，相当于“离群点”，随机森林预测结果的相对误差会有一定程度的提高。对多数预测样本点而言，自变量与预测变量间的非线性特性关系已通过训练集获得，且变量数值均处于变量均匀变化的范围内，预测效果通常较好。而29号样本点的点蚀电位数值为0.512 40 V，偏离训练集中的最大点蚀电位值0.485 47 V，两值之间偏差较大，该预测样本点可看成是“离群点”，预测效果不太理想。

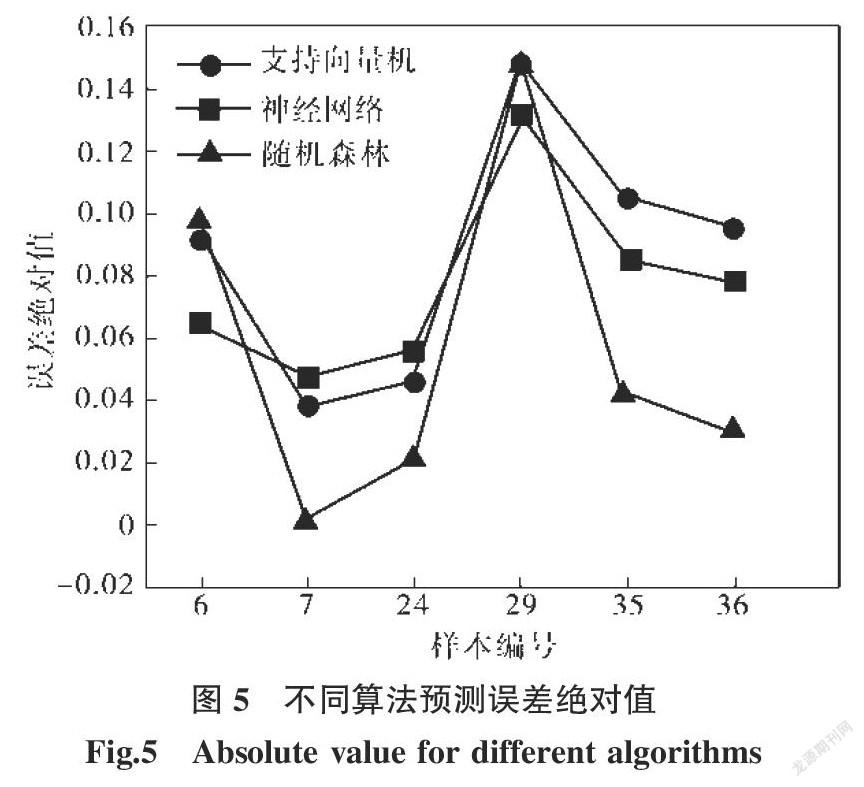
对比随机森林、BP神经网络及支持向量机预测结果误差的绝对值，如图5所示。3种方法对29号样本的预测结果均不理想，是所有预测样本结果中最差的。而对于其余样本点，随机森林的预测结果几乎都优于另外两种方法。事实上，绝大多数方法均对“离群点”比较敏感。当样本中出现“离群点”时，首先应从试验过程中考虑该结果是否有效，试验材料是否存在加工、组织缺陷，或是否有随机因素对试验结果产生影响等等。当试验结果准确无误时，需要探索更优化的算法，以提高预测的准确度。

4 结论

采用随机森林模型，对不锈钢点焊接头的点蚀行为数据进行建模，并选择、分析及评价模型参数，主要结论如下：

（1）通过“五折交叉验证”获得训练子集和测试子集的平均均方误差的变化规律，得到最佳节点备选变量个数为2。

（2）利用精确度平均减少分析变量重要性，电流平方对点蚀电位的影响最大，其次是焊接时间，电极压力影响最小。

（3）对比随机森林与神经网络、支持向量机算法预测结果，29号“离群点”样本预测结果都不理想;对剩余样本而言，随机森林的预测效果几乎均优于另外两种方法，预测相对误差绝对值均在10%以内，绝大多数样本点预测误差绝对值小于5%。

参考文献：

[1] Wei P S，Wu T H. Electrical contact resistance effect on resistance spot welding[J]. International Journal of Heat andMass Transfer， 2012（55）： 3320-3323.

[2] Florea R S，Bammann D J，Yeldell A，et al. Welding parameters influence on fatigue life and microstructure in resistance spot welding of 6061-T6 aluminum alloy[J]. Materials & Design，2013，（45）：460-462.

[3] Aslanlar S，Ogur A，Ozsarac U，et al. Welding time effect on mechanical properties of automotive sheets in electrical resistance spot welding[J]. Materials & Design，2008，29（7）：1430.

[4] Breiman L. Random Forests[J].Machine Learning，2001，45（1）：5-32.

[5] 李欣海. 随机森林模型在分类与回归分析中的应用[J].应用昆虫学报， 2013，50 （4）：1195.

[6] 陈华舟，陈福，石凯，等. 基于随机森林的鱼粉蛋白近红外分析[J]. 农业机械学报，2015，46（5）：233-238.

[7] 赵小欢，夏靖波，李明辉. 基于随机森林算法的网络流量分类方法[J]. 中国电子科学研究院学报，2013，8（2）：185-189.

[8] 张华伟，王明文，甘丽新. 基于随机森林的文本分类模型研究[J]. 山东大学学报（理学版），2006，41（3）：139-143.

[9] Malekipirbazari M，Aksakalli V. Risk assessment in social lending via random forests[J]. Expert Systems with Applications， 2015（42）：4624-4628.

[10] Martín ó，Tiedra P D，López M. Artifical neural networks for pitting potential prediction of resistance spot welding joints of AISI 304 austenitic stainless steel[J]. Corrosion Science，2010，（52）：2400-2401.

[11] 吳喜之. 复杂数据统计方法-基于R的应用（第二版）[M]. 北京：中国人民出版社，2013：37-40.

[12] 曹正凤. 随机森林算法优化研究[D].  北京：首都经济贸易大学，2014：67-71.