核心素养下小学数学模型思想如何在课堂教学中建构浅析

张雪紫

摘要：数学素养是属于认识和方法论的一种综合性思维模式，是我们通过对数学知识学习以及积累渐渐形成的一种概念化、抽象化、模式化的一种特殊认识品质，一般来说就是拥有数学思维的人们和周遭环境应用数学素养把数学概念和数学理论想结合处理实际事务的方式方法。数学建模是数学素养的重要表现形式，经过对数学建模可以把学生的综合实践能力优化提升，也可以对学生形成独自思维和大胆创兴的良好品质。在教学过程当中，着重培养学生的数学模型建设以及实际应用，可以为学生构建终生学习思维以及坚持不断学习创造坚定的基础。数学模型的建立基本可以分为三步：情境提问、构建模型、理解应用。

关键字：核心素养;数学模型;建构;模式;模型思想

对于构建数学模型来说最早可以最早追溯到人类开始使用数字的时代。随着人类使用数字，就不断地建立各种数学模型，以解决各种各样的实际问题。把具体实际问题进行实际分析、抽象、简化、最终得到和数学问题相似的问题，使用形式化的数学语言，解决实际生活问题。从广义的角度来说：数学模型就是只数学概念数学知识理论，他都是人们从生活当中的实际问题提炼出来的。从狭义的角度来说：数学模型其实就是指那些反應实际问题的指定的具体数学思想和具体数学结构原理。对于数学模型的建立基本上可以从三个方面出发：情境设问、构建模型、解决应用。

在国家《义务教育课程标准》的前言之中明确的对模型建立给出专业定位：建立模型思想是学生学会和理解数学同自己生活的外部世界确定联系的基本途径、建立和解决模型可以提高学习数学的兴趣和实际应用素养。建立和解决数学模型的过程主要是从实际生活或者是具体情况中抽象提出的数学问题，构成由数学符号建立的方程、不等式以及函数来对实际问题进行数学转化，构成模型当中的定量关系和变化规则，最终经过数学计算获得结果，并对得到的结果思考其中的实际意义并举一反三。

核心素养下模型思想如何在课堂实践中建构？建构过程中，应该注意哪些问题？在长期的教学实践中，有了以下理解。

一、“空间与图形”建构模式：生活问题——抽象本质——数学思想——推导公式——变换应用。

空间与图形的模型思想建构过程，普遍都是从生活实际问题开始，由此来展示数学问题出自于生活。利用实际生活问题，在对学生的教学当中，通过对学生的引导，让学生在学习之中经过对问题的观察和推敲还原问题的数学本质，从而完成生活问题到数学问题的转换，最后在有数学思想和数学原理来解决这些转化而来的问题。借助“数学思想”，如转化思想、归纳思想、分类思想、方程思想、数形结合思想等推导出公式模型并在“变换应用”环节深化建构。借助探索活动：对于平行四边形的面积计算举例。老师在学生对平行四边形的特征展开教学，把平行四边形用几条线段分成几个部分，根据学生掌握的平行四边形三角形以及梯形的特征，以及相关三角形、四边形形计算的基础上进行引导式教学。

教学片段：

（一）实际生活问题：

老师：为了能够让学校的空地都都铺上草坪，美化我们的校园环境，给我们的课外活动和日常课堂增添一抹绿色。

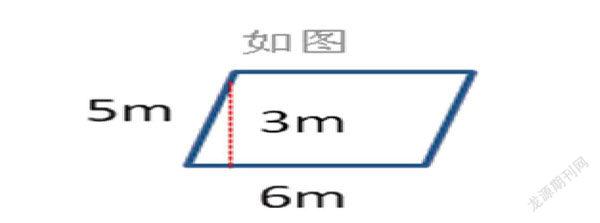
如下图：

作为学校的一份子，你们有什么好办法能够算出这块空地需要铺上多少平方米的草呢？

（二）抽象本质：师：同学们，我们要知道需要铺多少草，实际上就是要求我们做什么？

学生：求出这块外形是平行四边形的空地面积？

老师：请问大家可以用什么方法对此平行四边形空地面积进行计算呢？

学生1：可以数方格子的办法计算。

学生2：可以把这个平行四边形空地分割成我们学过的三角形和四边形的面积计算方法求和。

（三）数学思想：师：哦！原来我们可以迁移之前的学习经验，利用数方格子的方法可以近大致的算出这块空地的面积。那么如果让我们用数方格的方法去实际应用时是不是比较麻烦呢？

学生1：是的，一个一个数那么大一块地，难度大，有误差。

老师：那么我们试试另外一个同学说的方法，看能成功解决难题吗？把这个平行四边形空地分割一下，我们可以分成什么形状呢？沿着途中的那条线把它分割开来，移动在他的另一面，那么我们可以得到一个什么形状呢？大家一起在学习单上操作一下。

学生们：长方形

老师：那么长方形的面积怎么计算呢？我们之前学过的。

学生：长乘以宽。

（四）推导出计算公式：

老师：那么这回大家会计算平行四边形的面积了吗？你们小组是怎么做的？

学生：我们小组把平行四边形沿图中高剪开，分成一个梯形和三角形，把三角形移到另一边，拼补成长方形。发现：平行四边形的底部边长就是我们后来拼接成的长方形的长;平行四边形的这条分割线也就是平行四边形的高就是我们拼成长方形的高。所以求出平形四边的面积是6×3=18（㎡）（学生操作演示）

老师：这个结果与数方格的结果一致吗？

学生：一致。

老师：看来，我们这种解决实际问题的办法是有用的。这种方法体现了我们怎样的数学思想呢？

学生：转化思想。通过切割拼补把平行四边形转化成我们学过的长方形。

师：嗯，转化思想是我们数学学习中比较常用的数学思想方法。同学们要常用哦！哪位同学可以为我们再具体推导一下平行四边形的面积计算公式，以方便我们日后更加方便快捷地解决生活问题呢？

学生：长方形的面积=✖，

平行四边形的=长方形的，

平行四边形的=长方形的，

所以平行四边形的面积=。

老师：伟人说过实践出真知那么我们下面来具体检验一下学生的结论。请大家用这个平行四边形面积计算公式重新计算这道题。

学生3：运用公式计算，结果完全正确。

（五）变换应用：

老师：通过大家的通力合作，前面我们公共推导出平行四边形的面积的计算公式了，那么我们接下来在计算一个实际问题吧，举例：在某一个大商场的广场上有一个平行四边形空气，用来给顾客做停车场，它的底边长度为64m它的高为26m，一般每个汽车占地面积都是16㎡。那么这个停车场一共可以停放多少辆轿车？

学生：上面我们推导出的平行四边形面积计算公式：平行四边形的面积=长×高，所以64×26=1664（㎡），1664÷16=104（辆）

模型思想的构建以生活当中的实际问题为根本，教师从实际问题出发，引导学生建立数学模型，让学生对模型建立产生浓浓的兴趣。本例中“铺草坪美化校园环境”的问题情境有利于激发学生参与学习活动的积极性。模型思想建立的核心方式是老师的教学方式，在实际课堂教学过程当中，引导学生把身边的实际问题抽象为数学模型，充分感受模型思想带来的方便与快捷。兴趣是最好的老师，老师一旦把学生的学习兴趣提起来，那么学生的积极性也就跟着大大的提高，学生就会对课堂的实际教学听得津津有味，思维的马达就会轰鸣运转不停歇。老师在教学的过程当中要着重对数学思想方式方法进行提炼和深入体会，增减建立模型的思维厚度。提升建模的趣味。从具体的实际生活问题出发，建模、运算、总结。同时作为老师还要有变化的把实际问题转换情境和场合，引导学生深入了解某种数学模型，加深对数学模型的认知以及课后拓展。

二、“数与代数”建构模式：问题情境——尝试建构——得出模型——应用模型。

这类模式的教学活动开展，最重要的一步就是把实际问题情境转化成为一个学生们日常之中经常接触和了解的实际问题情境。引导学生进行实质性探究，在小组活动中进行尝试性建构。在建构的过程中，运用猜想、画图、折纸、演示等方式逐步加深认识，实现对某种特定数学模型的建立和应用过程。初步建构出公式、算理、法则、方程等模型后在进一步的变换运用中得到巩固，升华，进而完成建构。以“邮票张数”为例。

教学示范：

（一）案例情境：

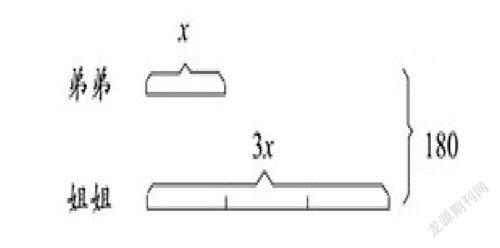
师：各位同学都有没有收集过邮票呢？收集过的请举手。现在大家看，晚饭过后，姐弟俩正和妈妈展示最近的集邮成果呢，（课件当中的情境图片所示）从图中你能观察到哪些是何数学相关的信息呢？

生1：姐弟俩一共有180张邮票。

生2：姐姐邮票张数是弟弟的3倍

师：你能提出一个数学问题吗？

生1：姐弟俩集邮各多少张？

（二）尝试建构：

师：我们今天就来探究用方程解决学生提出的问题：姐弟俩各集邮多少张？各位同学以小组为单位共同对这个问题进行探讨。

生1：我们小组的思路是：先写出题目中的等量关系：姐姐拥有的邮票张数和弟弟拥有的邮票张数相加总共有180张，并且弟弟的邮票张数的三倍是姐姐的郵票张数......

生2：我们小组的思路是画方框图表示他们之间的等量关系：

师：同学们都用不同的方式表示数量之间的等量关系，根据等量关系，我们设谁为未知数呢？

生1：应该设弟弟邮票为X张，则姐姐有3X张.......

（三）得出模型：师：那么我们可以根据大家提炼到的信息列出方程组来解决。

应用模型：师：假如我们现在把姐姐和弟弟一共有180张邮票改成姐姐的邮票数量比弟弟的多90张，那么我们现在可以这么列方程呢？想一想，与同伴交流一下。学生自主画线段图，根据题干的信息，列出等量关系方程式，求解方程并带入数字验证正确性。

数与代数中符号运算、方程思想也是模型思想的构建主要阵地。本例中“邮票张数”同样以日常生活中喜闻乐见的实际问题为元素，教师从实际问题出发，引导学生建立解形如“ax±x=b”的方程数学模型。在尝试建构阶段通过归纳概括、画线段图、方框图等方式方法让学生自主探究，用符号代替中文，写出等量关系式，初步建立方程模型解决问题的思维路线。本例中“尝试建构”环节是这节课的关键。当学生对模型思路有一定的经验认识后，模型才能得以初步建立。本例中，应用模型只是简简单单地将问题情境更改了一个条件，属于变式应用。刚建立的模型对学生而言并不代表模型已经牢牢建立在学生的思维模式当中，必须通过不断的实践应用，才能使模型真正在学生认知思维世界中“生根发芽”。

数学是一门关于研究数量、结构、变化以及空间模型概念的一门抽象学科，它对量进行演算并实际论证。是关于模式的科学。数学的产生基于人类日常生活的需要，是为人类解决问题服务的。人们需要解决实际问题的话，就需要根据实际问题建立想适应的数学模型，再由模型解决实际问题。模型思想在课堂教学中的建构成效起着举足轻重的作用。学生模型思想在课堂教学过程中的建构策略必须从学生的实际出发，在不断的实际探知过程中，不断的探究、观察、总结计算，最后得到应用于实际生活当中的数学模型，共筑和谐美好生活。

参考文献：

[1]义务教育《数学课程标准》（2011年版）北京师范大学出版社

[2]小学数学义务教育课程标准（2011年版）案例式解读丛书教育科学出版社

[3]《核心素养导向的备课》主编吴筱玫天津教育出版社