刍议高阶思维视域下简便运算的教学策略

沈君

摘要：思维培育是数学教育的重要任务。文章以简便运算的教学为例，尝试以错题解读为切入点，思考数学教育的旨归，从教材解读、多元表征、辨析讨论、开放练习等角度探寻培养学生高阶思维能力的教学策略。

关键词：小学数学 高阶思维 简便运算

简便运算是计算教学中的重要组成部分。它建立在四则运算的基础上，要求学生运用运算律，根据算理简化较复杂的运算，提高速度和正确率。实际应用中，由于简便运算类型多样，变式复杂，许多学生运算时往往不知所措、错误频出。因此，厘清教育发展定位，变革陈旧教学模式，在知识传授的同时进行高阶思维培育，是改变现状的有效途径。

一、错题分析，初窥学生思维现状

简便运算是计算策略化和最优化的综合，也是学生思维能力的综合体现。从学生简便运算中部分错题情况来分析学生的思维状态，以反思教学方式不足。

错例1：42÷（7+7）

题型分析：在本题中，常有学生把乘法分配律与之混淆，用42分别除以两个7，强行简算。这个题目错误率在高年级较中年级更高，主要是学生在了解乘除互逆运算后，将之与头脑中的乘法分配律进行混淆造成。

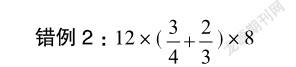
题型分析：有部分学生将括号内先通分再展开计算，还有部分学生注意到可使用乘法分配律，却忽视了乘8。这说明部分学生缺乏整体思维，只发现该题有部分乘法分配律的呈现，而没有注意到题目的本质是三部分相乘，将本题视作新类型束手无策。

学生的种种错误，折射出其思维训练的不足。真实的数学情境往往状态新奇、多条件并存，学生需要运用已知的信息分析、综合和评价，多法并举才能解决。

二、立足学生发展，思考数学教学旨归

高阶思维就是指发生在较高认知水平层面上的心智活动或认知能力。它是建构高阶能力的核心，是提出问题能力、批判性思维能力、反思质疑能力和创新能力生发的源泉，是促使儿童数学向上生长的重要力量。

陶行知先生曾提出“要以学生的发展为本”。数学教育不应仅停留于传授基本知识与基本技能的较浅层面，而应着眼于适应社会和学生的终身发展。在教学中，教师应关注数学思维的培育，精心设计活动，让学生能在真实的数学模型中阐释观点、交流方法、感悟意义、优化方法，提升高阶思维发展。

三、高阶思维视域下简便运算的教学策略

在课堂教学中，教师应站在思维培育的角度，调整教学的策略，在教学中恰当地处理教材、表征、辨析、练习之间的关系，把握教学本质，提高思维培育质量。下面仅以简便运算中乘法结合律的教学为例，浅议高阶思维视域下简便运算的教学策略。

1.三维读教材，把握教育任务

事实上，学生在学习运算律之前，早已不知不觉地用上了这些规律。例如，二年级计算进位加法24+8：24+6=30，30+2=32。这里就运用了加法结合律。简便运算教学的真正教育目的不仅是掌握运算律的表达形式及应用运算律进行简便计算，而是让学生在经历归纳、抽象、辨析与质疑的过程中，自然生发高阶思维，从而在现实生活中自然地进行运用。把教材中显性的知识要点、隐性的教育任务与实用的数学价值结合在一起，就构成了解读教材的三维视图。

2.多元化表征，激活思维

曹培英教授曾说过，小学数学的核心问题是适度抽象，谋求儿童思维的形象性与数学的抽象性的协调统一。因此，教师在教学中可以通过多元表征的方式帮助学生理解知识，让算理说得通、看得见、悟得透。

（1）言语表征

教学时，教师可以让学生用自己的话来说说乘法结合律的意思。有的学生会直接用字母表达式，即（a×b）×c=a×（b×c）。这时，教师可以进一步启发，如果把a 、b、c看作三个乘数，那么这个表达式是什么意思？学生可以说出：三个乘数相乘，可以先把前两个乘数相乘，也可以先把后两个数相乘，结果不变。这样，学生不仅能在认知上理解规律，而且能够通过语言进行表达。

（2）图形表征

将抽象的数学运算与形象、直观的图形进行相互转化，是让学生理解算理、迁移算法的有效路径。在乘法结合律的教学中，教师可以用数字举例，以3×2×4 配点子图，可以先横着看，得到3×2，再一行一行地往下数，就可以得到3×2×4；也可以先竖着数，发现左边有3×4个点子，再往右发现有这样的两部分，进而得到3×2×4；还可以把3个点子当作一个整体，先数一数一共有几个3，发现一共有2×4个，然后得到结果3×2×4。

在教学中，教师借助图形使学生明白了算理的内在本质。数与形的相互辅助，让学生实现了认知上的飞跃，完成了抽象到具象之间的转化，实现了思维的可视化。

（3）符号表征

教学中，教师可以让学生再列举一些这样的算式。通过观察、计算、比较，学生提出这些算式的结果都是相等的。在此基础上，教师可以让学生用自己喜欢的方式来表达这样的算式。有的学生会采用圆圈、方块、三角来组成算式；有的学生会用甲、乙、丙表示三个数合成算式，还有的学生则尝试用不同的字母来表达式子间的关系。这样的操作活动，不仅使学生经历了不完全归纳的过程，更让学生的思维水平由表象水平上升到抽象水平。

3.辨析大讨论，促进思维发展

《义务教育数学课程标准（2011版）》指出，“要寻求合理简洁的运算途径解决问题”。例如，在教学540÷36 时，学生可能会出现540÷4÷9、540÷9÷4、540÷6÷6、540÷2÷18、540÷18÷2等多种解法。教师通过引导学生观察、交流，让学生自发产生思考、辨析、质疑与评价。交流中，学生发现第一种和最后一种的第一步540÷4和540÷18都要通过笔算；540÷2个别学生易误算。在对比中，学生自主选择了最易计算、最不容易出错的解法。在个体或群体为了做出决定而进行的分析、交流、判断与选择的过程中，学生形成了深刻、理性的认知，同时促使思维迈向高阶发展。

4.创意微练习，丰盈高阶思维

教学的本质是知识的再创造。教师要为学生参与数学活动提供足够的时间和空间，让学生有条件、有机会去观察、尝试、思考、讨论，促使学生将经过自己的亲力亲为转化为知识的再生成、再创造。

例如，在教學简便运算时，教师让学生用自己喜欢的方法计算25×44。有的学生用25×4×11，有的用25×40+25×4，有的交换乘数位置，用44×5×5计算，还有的学生列式44×100÷4。由最后一种解法，部分学生甚至联想到44×5×10÷2。学生的运算方法没有依靠教师现成的说教，而是创造性地大量生成。多角度、多策略思考问题，创造性地解决问题，这正是高阶思维追求的灵活品质。

综上所述，思维培育是数学教育的重要任务。教师应当在理解教材的基础上，采用多元的通道，引导学生在学习中进行表征、辨析和创造，发展高阶思维的能力，赋予儿童数学向上生长的力量。

参考文献

[1]冯贵群.言语与符号：培育学生思维的重要表征[J].教学与管理，2019（07）：34.

[2]赵瑞生.在算术运算的教学中培养学生的准变量思维[ J].江苏教育，2013（33）：11.

[3]孔凡哲，史宁中.中国学生发展的数学核心素养概念界定及养成途径[ J].教育科学研究，2017（06）：5-11.