HPM视野下高中立体几何教学研究

俞文锐

摘要：立体几何教学在培养学生几何知识与空间想象力等方面有着关键性的作用。文章在分析HPM视野下，高中立体几何教学的价值的基础上，以《空间中直线与直线的位置关系》为例，探索HPM视野下高中数学立体几何教学策略。

关键词：HPM视野 高中数学 立体几何

立体几何拥有悠久的历史，不仅能够培养学生的空间想象能力，发展学生的空间观念，而且立体几何也是平面几何的延伸，是空间解析几何的基础，在教学中起着承上启下的作用。然而，随着向量的引入，立体几何在培养学生空间想象和锻炼学生综合思维能力方面有所减弱。而且，在课堂教学中很少融入文化元素，致使学生在利用传统几何中的逻辑推理解答立体几何题目时，往往死记硬背、机械操作，而数学史（HPM）能够有效激发学生学习的兴趣，澄清数学知识的本质，有助于在科学和人文之间建立桥梁。因此，在HPM视角下探究高中立体几何教学具有重要的意义。

一、HPM视野下高中立体几何教学的价值

1.激发学生探索兴趣，改善课堂气氛

“兴趣是最好的老师。”不同于传统教授式的学习方式，数学史更加注重学生的探究过程，能够促使学生感受到主动探索知识的乐趣，积累基本活动经验，从而让课堂气氛变得更加活跃。以《空间中直线与直线的位置关系》为例，数学史的融入能够激发学生关于公理与定理之间关系的讨论，促使学生思考直线在空间中的形象，从而引导学生探索空间中直线与直线的位置关系。

2.探寻发生过程，促进知识理解

陶行知先生说：“先生所教授的知识，不是僵化的、死的知识，应要引导学生不仅要知其然，还要知其所以然。”在立體几何教学中融入数学史，能够让学生明白，数学思想和方法不是直接得到的，而是由无数数学家不断演化、探索获得的，从而促使学生探寻知识本源，探寻知识发生过程。以《空间中直线与直线的位置关系》为例，数学史的融入能够让学生明白一个公理需要相当数量的数学家经过演算和推理才能建立，也就是“平行于同一条直线的两条直线平行”这条公理是有根可循的，完全是可以证明的。

3.品味数学文化，培养正面情感

数学史的融入能够让学生体会数学知识与生活之间紧密的联系，认识不同数学文化形成的多元文化。同时，激励学生学习众多数学家的探索精神，拓宽学生的思维，有效培养学生的正面数学情感。以《空间中直线与直线的位置关系》为例，数学史的融入可以让学生体会到转化、化归、反证法等数学文化，认识到欧几里得等数学家的数学精神和信念。

4.经历数学抽象，加强空间想象

数学史的融入能够让学生经历公理化、形式化等抽象定义的过程，能够有效锻炼学生数学抽象等能力。以《空间中直线与直线的位置关系》为例，教师可以引导学生通过增添辅助线、勾勒草图等方式对定理进行推导证明，从而有效锻炼学生的空间想象和空间推理等能力，发展学生的空间观念。

二、HPM视野下高中立体几何教学实践

HPM视野下高中数学立体几何教学理应是理论联系实际的，而异面直线处于立体几何的入门阶段，在实践方面，需要多观察实物模型；在理论方面，需要与平面几何知识做对比和类比。因此，为了研究的深入，笔者以《空间中直线与直线的位置关系》为例，探索HPM视野下高中立体几何教学策略。

1.复习旧知，引出课题

为了更好地研究空间中直线与直线的位置关系，教师应通过考一考、问一问的方式组织学生回顾已学知识。例如，平面的两个特性、三条公理以及公理的推论，促使学生理解公理与定理之间的区别，理解平面没有厚度、无限延伸的两个特性，以及如何确定一个平面以及两个平面如何相交。在此基础上，从而引出线线之间的关系，进而引出课题。

2.直观感知，建构概念

为了初步建构概念，教师应以日常生活中常见的物体为例初步感知。如图1所示的正方体是我们日常教学中常见的图形，要求学生在回顾平面中线线之间平行和相交两种关系的基础上，引出平面AA1DD1中直线DD1与平面BB1CC1中直线BC既不相交也不平行的新型位置关系，即异面直线，并要求学生对照上述异面直线的特性，列举日常生活中常见的异面直线情形。例如，天安门广场上，旗杆所在的直线与长安街所在的直线；教室内的日光灯管所在直线与黑板的左右两侧所在的直线等。

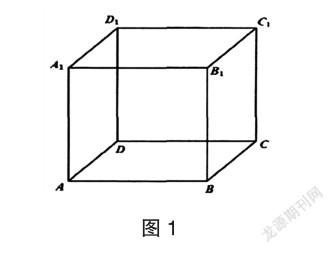
同时，要求学生通过画一画的方式，思考如何在数学中表述出异面直线，并在学生探究的基础上，通过演示的方式呈现出了以下两种异面直线规范画法，如图2、图3所示。

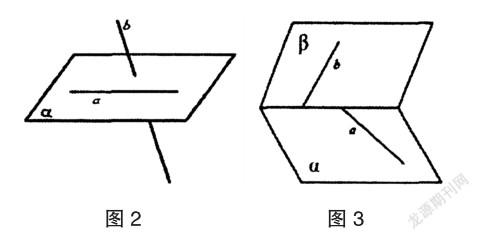
随后，引导学生总结得出异面直线的定义，特别是对于一些不严谨的说法，教师应鼓励其他学生通过反例的形式加以讨论和证明。例如，有学生总结出异面直线就是不在同一个平面上的两条直线，此时，教师应及时引导学生通过反例的形式加以验证，从而得出如下异面直线的定义，即不在任意一个平面中的两条直线就是异面直线。

3.探究概念，引出定理

对于初次接触异面直线的学生来说，上述定义较为抽象。教师可以组织学生利用教具摆出不同位置的两条异面直线，然后要求观察所呈现异面直线之间的区别。与此同时，引导学生回顾在平面角教学中是如何表示两种不同的倾斜状态，并以日常生活中建造立交桥为例，思考不同角度下的立交桥，从而引出异面直线所成角的概念。

随后，引导学生思考异面直线所成角的概念与平面中夹角概念之间的区别和联系，并在此基础上得知异面直线所成角的概念实质上就是平面中夹角概念的推广。并思考异面直线所成角概念中由于点o是任意选取的，那么是否对于所成角的角度有影响，从而引出等角定理，并通过如图4所示的图形让学生探索证明方法，从而展现出历史上欧几里得的证明。

4.设置疑问，历史重现

在上述等角定理证明过程中，如果两条直线和同一条直线平行，那这两条直线就平行。这样的结论在平面几何中是正确的，那么在空间几何中是否还能成立？因此，教师应以此为疑问，要求學生以所学知识为根基，思考是否可以将上述结论推广到空间几何中，并思考如何尝试证明。显然，对于这样的疑问，学生利用现有知识是无法正确解答的。因此，教师可以通过视频的形式重现历史上空间平行线的传递性质探究过程，即呈现欧几里得与几何原本，重点突出欧几里得的几何无“王者之道”。然后讲述Playfair、Legendre、Thompson等数学家对于空间平行线传递性质的证明，最后讲解历史上出现过的两个错误证明，鼓励学生要在学习过程中养成探索和质疑的意识。

5.巩固练习，总结提升

以本节课程的收获和疑惑为主题，要求学生总结出本节课程的知识点，指出空间中直线与直线的位置关系经历了漫长的发展历程，要求学生深刻体会这些历史上做出贡献的数学家的数学精神，并要求学生独立完成如下练习题目：

如图5所示，已知空间四边形ABCD，AE=EC，BF=FD，若AB⊥EF，AB=2，CD=4，试求EF与CD之间的夹角。

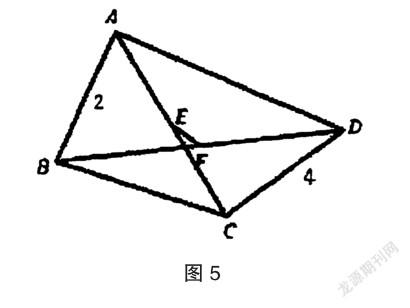
三、HPM视野下高中立体几何教学反思

在具体实践教学中，HPM视野下的空间中直线与直线的位置关系课堂教学还需要注重以下几个问题：

一是在角的概念推广过程中，有极少部分学生对于两条异面直线所形成的夹角概念存在一定的疑惑，两者是否存在历史相似性还有待考证。若两者确实存在历史相似性，则在设计异面直线概念时应体现更多元素。

二是在数学史素材融入教学材料分析时，可采用附加、点缀、复制、顺应、重构等方式融入，可以从趣味、科学、可学、有效和新颖等方面对史料进行挑选，从而有效增加文化和人文元素。

三是在重现空间平行线的传递性质等视频时，教师应鼓励学生充分挖掘历史上数学家在探究过程中所涌现的精神，而不是只停留在感兴趣的层面上，只注重他们做出的具体贡献等。

四是由于缺乏具体的实验，学生的注意力难以长时间集中。因此，教师应在引导学生总结得出定义和定理时，通过适当的提问引起学生的注意力。同时，在课堂教学过程中，要在听、说、读、写、画等方面不断转换。

总之，HPM视野下高中立体几何教学能够激发学生学习的兴趣，培养学生逻辑思维和空间想象能力。在具体教学实践中，教师应充分借鉴历史、呈现历史、开发对数学及其社会背景的深刻意识，并通过附加、复制、顺应、重构等方式，体现数学史的文化之魅、方法之美、探究之乐、能为之助、德育之效、知识之谐等价值。在理解立体几何基本内容知识点之外，解决很多历史上的“为什么”问题，从而有效提高高中立体几何教学质量和水平。

参考文献

[1]曾泽群，赖宝禧.HPM视角下的“勾股定理”教学设计[J].数学教学，2019（9）.

[2]汪晓勤，王苗，邹佳晨.HPM视角下的数学教学设计：以椭圆为例[J].数学教育学报，2011（10）.