从天体运动中的追及和相遇问题说开去

◇ 山东 李庆艳 王明洲

在一条直线上的追及和相遇问题是直线运动教学的重点,圆周运动中也有追及和相遇问题,在高考中经常出现,特别是考查万有引力与航天中的追及和相遇的问题更是屡见不鲜.

1 天体运动中的相距最远和最近问题

天体运动中的追及和相遇问题,即为天体运动中的相距最远和最近问题,从两星相距最近开始到下一次相距最近两星转过的角度之差为2π,从两星相距最近开始到第一次相距最远两星转过的角度之差为π.

A.4 B.6 C.7 D.8

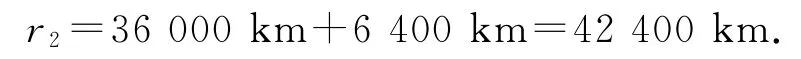
两个轨道半径的关系是r2＝4r1,由开普勒第三定律可得,解得.某时刻宇宙飞船和同步卫星相距最远,假设经过时间t1二者相距最近,则有,其中T2＝24h,解得t1＝,设再经过时间t2二者下一次相距最近,则有,解得

因此,在24h内,地面上的接收站一共接收到7次电磁信号.选项C正确.

2 从相距最近和最远引申出天体运动中的几何关系

天体相距最近和最远是非常特殊的几何关系,在天体运动中,如果避开相距最近或者最远考查几何关系,则题目难度将加大.

(1)B 卫星的周期；

(2)A 卫星和B 卫星不能直接通信的最长时间(电磁信号传输时间不计).

(2)设A 和B 卫星不能直接通信的最长时间是t,A 卫星转过的角度是α,B 卫星转过的角度是α′,那么两颗卫星不能直接通信是指它在图1中的B 点和B′点之间,内圆是指地球的赤道,由几何关系得,B 卫星因为轨道半径小,运行得要比A 卫星快,有如下关系：α′－α＝∠BOB′,解方程得

天体运动中两卫星的最近和最远及其他几何关系问题,既是对空间想象力的考查,又是对应用数学知识解决物理问题能力的考查,很好地体现了物理学科核心素养中的物理观念和科学思维.解决该类问题,万有引力和圆周运动有关知识是基础,挖掘隐含条件是关键.

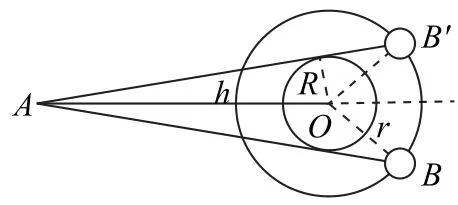
图1