巧用正交分解,速求电场强度

◇ 山东 孙 扬 董蓓蓓

已知匀强电场中若干点的电势,求解匀强电场的电场强度,是静电场中比较常见的一种题型,求解该类问题最常用的一种方法是“等势点法”,等势点法的关键是寻找等势点,画出等势面,确定电场线,最后由电场强度的大小与电势差的关系求解.但教学实践表明,学生在运用等势点法求解时,效果并不理想,通过询问学生发现问题出在几何图形的构建和几何关系的寻找上.那么有没有其他的解法可以避开几何图形的构建和几何关系的寻找呢? 答案是肯定的,下面笔者结合例题介绍另外一种方法：正交分解法.

1 正交分解法的缘起

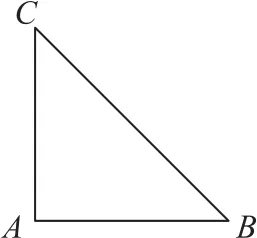
图1

解法1等势点法

由题意可知,BC 边上一定有一点电势为0,设为D 点,连接AD 为一条等势线,过B 点作AD 的垂线交AD 于P 点,设∠DAB＝α,如图2所示.则

解得α＝60°,即电场强度的方向与BA 间的夹角为30°,E＝40V·m－1.

解法2正交分解法

以A 点为坐标原点,BA 为x 轴,AC 为y 轴建立直角坐标系,设电场强度E 在x 轴方向的分量为Ex,在y 轴方向的分量为Ey,E 方向与x 轴间的夹角设为β,如图3所示.则有

解得E＝40V·m－1,β＝30°.

图2

图3

通过等势点法和正交分解法两种方法的比较,不难发现,正交分解法的优势在于有效避开了几何图形的构建和复杂的几何运算,既体现了物理问题的本质,又使电场强度的求解变得简单易行,不失为一种好的方法.

2 正交分解法的应用

图4

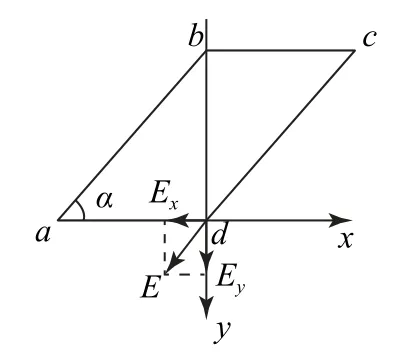
图5

综上所述,在匀强电场中,若已知三点的电势,且该三点间的连线构成一直角三角形时,便可运用正交分解法求解匀强电场的电场强度.相比等势点法,这种方法思维流程短,运算量小,学生更易于掌握,并能有效地规避错误,提高学生求解问题的准确性.