基于不确定性的高速公路路线方案比选方法研究

祝文君

（中国市政工程中南设计研究总院有限公司，武汉 430010）

对于高速公路建设项目，线路走向是否科学合理不但关系到工程的经济收益、建设成本，还会直接影响到周边城市的旅游、矿产等资源能否得到充分开发，能否促进贫困地区经济的发展以及满足国防建设的需要等. 因此，作为建设前期需要解决的重要问题即高速公路路线方案比选，除了要考虑主要技术标准、投资成本等技术和经济上的定量指标，还要分析工程对周边环境的影响、对贫困地区经济发展的带动作用等定性指标，而且在某种程度上这些定性指标的作用更加突出.

在国外研究中，人们最先关注方案的经济成本，如文献［1］中Dupuit J提出的费用和效益理论被广泛应用于项目方案的选择；20世纪末美国哈佛大学Dompere K K［2］提出的层次分析法，对于解决模糊决策以及利润比选问题提供了科学依据. 随着政府及人民对环保意识的加强，路线方案比选也逐渐将环境比选加入重要指标进行考虑，David J R和Tony F［3］提出的“压力-状态-响应”（PSR）模型，为设计、决策人员进行方案的环境比选提供了依据. 国外对公路路线的技术设计方面也取得了显著的成就，主要包括将GIS 软件、AHP、模糊数学、神经网络、遗传算法、熵和熵权等理论和方法应用于公路路线综合比选中，从技术层面保证公路路线方案评价技术及优选技术的科学合理性［4］.

在国内研究中，傅荧［4］针对费用效益分析法的缺点，即不能量化直接效果外的效果，提出改进的费用效益分析法，给决策者提供更多的参考价值；雷岩［5］通过对方案比选中经济因素的总结，提出了基于基金评价的经济指标体系，并成功应用到项目中. 进入21世纪后，RS、GIS等技术已经可以通过对三维空间进行环境分析及模拟，实现公路路线方案定量化的环境比选. 自此，生态环境评价方法已由最初的专家定性分析逐渐发展到定量方法计算的阶段. 苏万军［6］和陈毕新［7］考虑项目建设时经济与环境的损失情况，通过构建数学模型求解最优方案. 随着公路建设项目的逐渐复杂化，公路路线方案决策也随之复杂，因此专家学者开始将多目标决策方法引入到方案比选中以解决决策复杂化问题. 如刘志军等［8］将方案比选看作是多目标决策问题，基于AHP法构建的评价指标体系基础上建立模糊优选模型. 赵康［9］构建了12个环境影响路线比选方案评价指标，并提出将其与AHP法、模糊数学等多目标决策方法结合进行公路路线的优选.

多年来，尽管国内外学者针对路线方案比选开展了大量的研究工作，但上述研究方法选取指标包含经济、工程技术、环境、社会影响等指标，对于路线方案中的安全指标研究较少，同时方案中的定性指标在处理时，不能全面地考虑指标的不确定性. 本文正是基于该背景下将安全因素引入路线方案比选评价中，对评价指标体系的定性指标通过云模型理论进行相应转换，减少传递过程中的不确定性，为路线方案的安全比选评价、决策提供可靠准确的依据. 为此，本文提出基于云模型的高速公路路线方案比选方法，从地形地质条件、线形协调性和设计要素、危险路段和路侧危险、路网布局和大型构造物分布5方面分析其对高速公路路线安全的影响，建立了高速公路路线方案安全评价指标体系，通过云模型及组合赋权方法，建立了基于不确定性的高速公路路线方案比选方法，为路线方案比选决策者提供参考及依据.

1 评价指标体系的建立

高速公路路线方案安全比选首先需要解决的问题就是方案指标的选取，但目前研究方法尚无对路线安全比选的统一标准，本文从地形地质条件、线形协调性和设计要素、危险路段和路侧危险、路网布局和大型构造物分布、恶劣天气影响5个方面进行分析，选择了地形条件、不良地质条件等20 个定性和定量指标［10-16］，建立了高速公路路线方案安全比选评价指标体系，并将体系中的各指标按照定性、定量指标；效益型、成本型指标进行划分，方便后续计算. 结果如表1所示，可按照实际线路方案的性质（原则方案、局部方案等）对指标进行相应的调整.

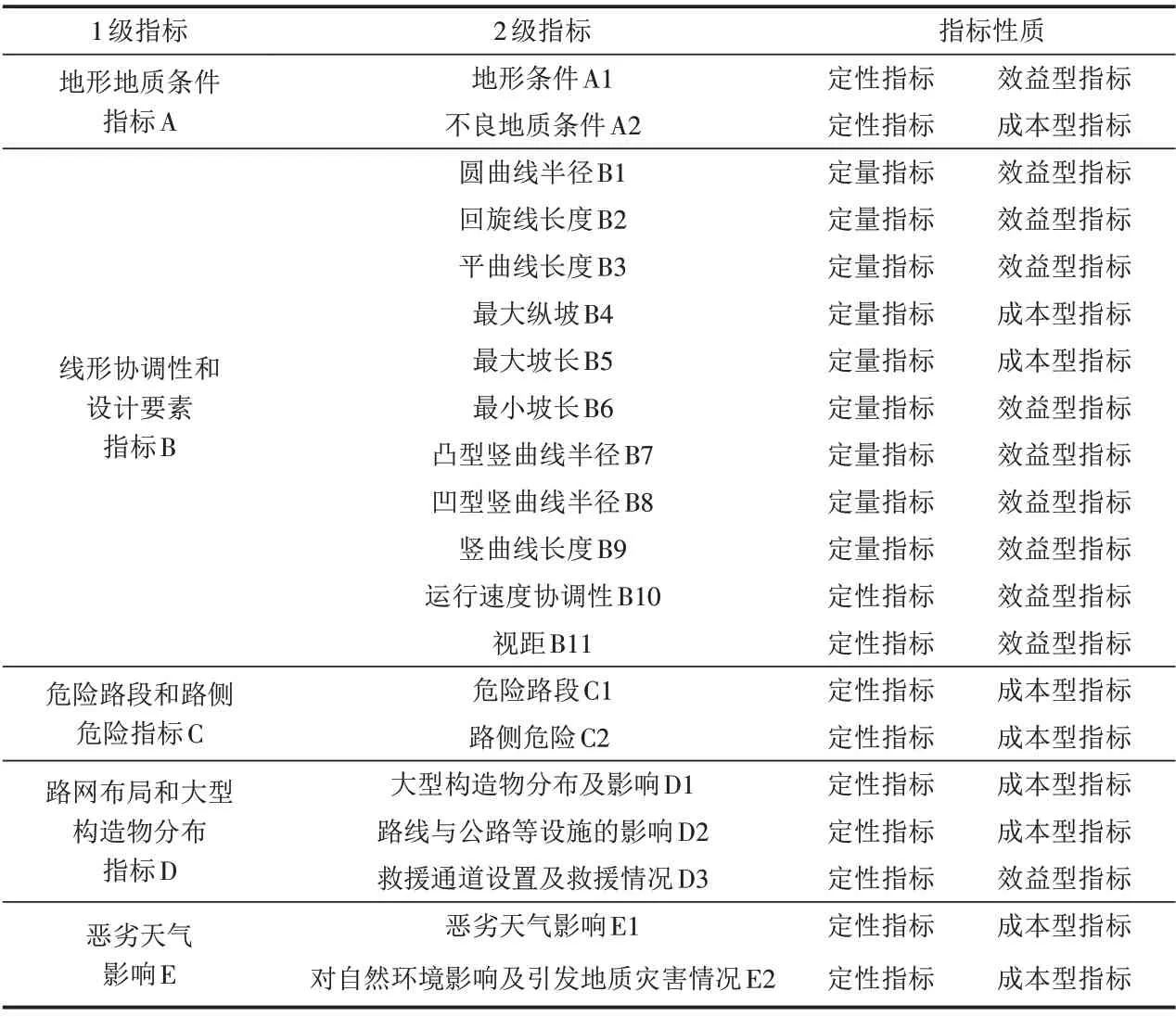
表1 高速公路路线方案安全比选评价指标体系Tab.1 Highway route plan safety comparison and selection evaluation index system

2 云模型理论

2.1 云的基本概念和数值特征

设μ（x）：U→［0，1］为论域U中的任意一个元x素对定性概念的隶属度，则所谓的云即为μ（x）在U上的分布，这里的x叫作云滴，是云最基本的组成元素，也是定性概念的一个量化值［17］.

云模型理论中，对一个定性概念的描述是通过3个数字特征（Ex，En，He）［18］来完成的，其中，Ex称为云滴群或云的期望，En称为云滴群的熵，He称为云滴群的超熵. Ex表示定性概念量化为云滴群的中心点；En 反映了云滴群分布的不确定性；He则进一步表征定性概念量化为云滴群的离散性. 通过使用（Ex，En，He）来表征一个定性概念，并作为定性与定量间转换的工具，充分考虑了转换间的不确定性及离散性.

为了更好地理解对云模型的三个数字特征，以定性概念“青年人”为例，图1 表示“青年人”的一维正态云图.

从图1 中可以看出，Ex 是定性概念的中心值，是最能代表定性概念的典型样本点；En 是表示定性概念能被接受的范围区间；He是En的不确定性度量，它的大小与云的“厚度”呈正相关关系.

2.2 基于云模型的不确定性推理及云发生器

定性概念可通过云模型的单规则不确定性推理来量化，推理的基本形式为：如果“定性概念T1”，那么“定性概念T2”. 然后将概念T2转化为（Ex，En，He），再根据（Ex，En，He）采用如下的算法生成由任意多个云滴（云滴群）组成的正态云，这种云的生成方法称为正向云发生器.

1）根据T2的数字特征（Ex，En，He），生成以En为期望、He2为方差的正态随机数En′i；

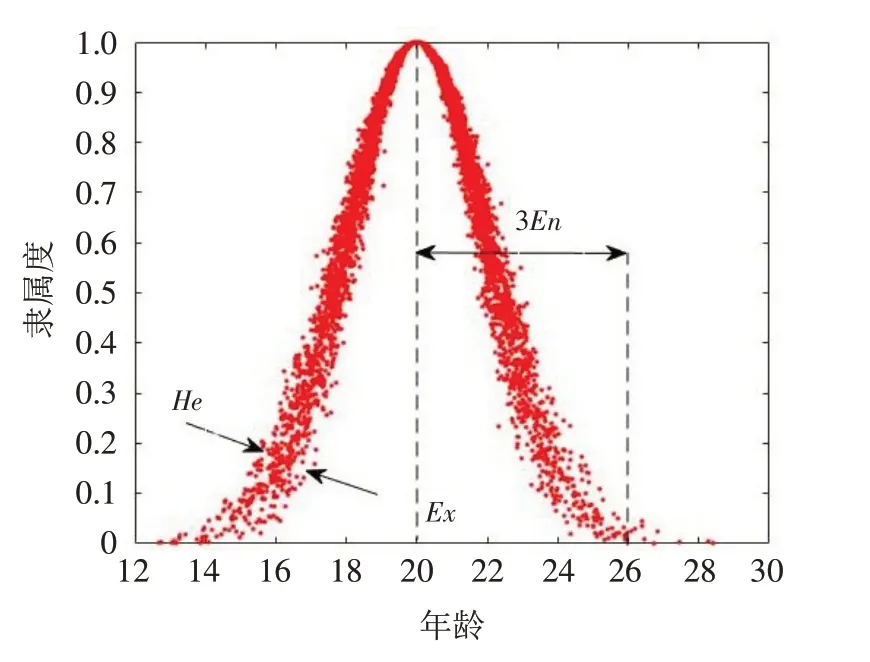
图1 “青年人”的一维正态云图Fig.1 One dimensional normal cloud chart of“Young People”

4）生成N个具有确定度ui的云滴xi.

3 基于不确定性的高速公路路线方案比选方法

指标的权重是指在评价过程中评估对象的每个指标在整个系统中影响程度的比例，权重分配的准确性将直接影响评估结果. 目前，主要分为主观赋权法、客观赋权法和组合赋权法3种. 主观赋权法虽然可以在吸收专家经验的基础上，反映出各指标的重要程度，但其缺点即是主观性强；客观赋权法虽然可以有效避免主观性强的缺点，但最后计算的权重值可能出现与实际情况相违背的情况. 针对主观、客观赋权法存在的不足，本文提出以G1法与熵权法结合的组合赋权法，并在确定权重前，将定性指标通过云模型转换为定量数值，减少传递过程中的不确定性，并在高速公路路线方案安全比选中进行实例应用.

3.1 G1法确定主观权重

G1法的原理是通过专家的知识、经验判断出各指标间的序关系，并给出重要程度赋值，计算步骤如下.3.1.1 确定序关系 设评价指标体系中存在n个评价指标，记为x1，x2，…，xn，对于评价总目标，若评价指标xi的重要性程度大于xj时，则记为xi≥xj. 对于n个指标，若存在x1≥x2≥…≥xn，则认为n个指标建立了序关系，并可按照以下步骤来确定序关系：

1）在评价指标集｛x1，x2，…，xn｝中，专家依据评价总目标的需求选出仅且一个认为最重要的指标，记为x1*；

2）在剩下的n-1个指标中，专家选出仅且一个最重要的指标，记为x2*，以此方法进行挑选；

3）挑选了n-1次后，评价指标集中仅剩余唯一的一个指标，记为xn*；按上述步骤进行挑选后，则认为确定了序关系.

3.1.2 相对重要程度分析 将指标xk-1与xk间的重要程度之比记为ωk-1/ωk，比值结果为rk（k=n，n-1，…，2），序关系的具体赋值见表2.

若专家给出的rk不在表2范围内，则序重新进行指标重要度评价.

3.1.3 权重系数计算 根据专家对指标间的重要程度赋值，计算出某指标的权重ωn为：

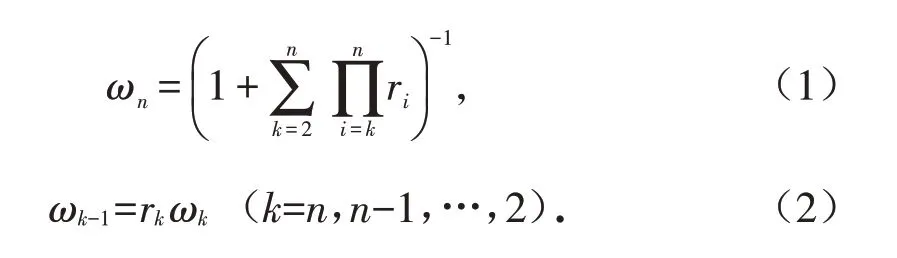
表2 赋值参考表Tab.2 Assignment reference table

3.1.4 群决策结果的确定 设有t为专家参与决策，记第k位专家的权重指数为Lk，第k 位专家的第i 项指标权重记为，则第i个指标的群决策结果为［19］：

表3 专家熟悉程度赋值表Tab.3 Expert familiarity rating table

其中专家的权重指数计算按照专家对路线方案安全比选的熟悉程度进行不同的赋值（dk），并熟悉程度分为四个等级，各专家熟悉程度赋值情况见表3.

根据表3，即可得出第K位专家的权重指数：

3.2 熵权法确定主观权重

设有m 个路线比选方案X=｛X1，X2，…，Xm｝可供选择，方案中有n 个评价指标，指标集表示为A=｛A1，A2，…，An｝，在指标集中R存在定性指标Rj（j=1，2，…，k）和定量指标Rj（j=k+1，…，n）. 对于方案Xi，定性指标Rj（j=1，2，…，k）采用语言模糊数作为其取值，定量指标Rj（j=k+1，…，n）的取值则为一个确定的数值. 语言类模糊集为S=｛很大，大，较大，一般，较小，小，很小｝或S=｛很好，好，较好，一般，较差，差，很差｝.

通过将语言类模糊数作为定性指标的取值，不仅将取值边界进行了模糊化，而且充分考虑了定性指标的不确定性，更加符合人类对定性概念的描述习惯. 基于云模型的高速公路路线方案安全比选的一般步骤如下.

Step1 利用云模型的不确定推理对定性指标进行量化，过程如下：

1）采用语言类模糊数｛很高、高、较高、中等、较低、低、很低｝来描述定性指标得分的高低，其对应的云模型描述如表4所示.

2）通过云模型的不确定性推理，将定性指标的语言类模糊数取值转换为对应的云模型描述，现以定性指标“对自然环境影响及引发地质灾害情况”为例，利用专家的知识建立不确定性推理规则：

If 对自然环境影响及引发地质灾害情况“很大”，Then 因子作用分值“很低”，则对应的云模型描述为（10，20/3，0.02）；

If 对自然环境影响及引发地质灾害情况“大”，Then 因子作用分值“低”，则对应的云模型描述为（30，10/3，0.02）；

表4 因子分值高低的定性评语与云模型描述的关系Tab.4 Relationship between qualitative comments and cloud model descriptions

If对自然环境影响及引发地质灾害情况“较大”，Then因子作用分值“较低”，则对应的云模型描述为（45，10/3，0.02）；

If对自然环境影响及引发地质灾害情况“一般”，Then因子作用分值“中等”，则对应的云模型描述为（55，10/3，0.02）；

If对自然环境影响及引发地质灾害情况“较小”，Then因子作用分值“较高”，则对应的云模型描述为（65，10/3，0.02）；

If对自然环境影响及引发地质灾害情况“小”，Then因子作用分值“高”，则对应的云模型描述为（80，10/3，0.02）；

If对自然环境影响及引发地质灾害情况“很小”，Then因子作用分值“很高”，则对应的云模型描述为（90，20/3，0.02）.

Step2 根据定性指标取值的云模型描述，采用云滴的正向发生器算法，按照最大隶属度原则计算各比选方案各项定性指标的得分，记为rij（i=1，2，…，m，j=1，2，…，n），这样与定量指标的取值一起，构成路线方案评价的决策矩阵，记为R=（rij）m×n.

为了消除量纲的影响，需要对决策矩阵进行规范化. 按照表1 中对指标性质的划分，采用公式（5）、公式（6）进行规范化的处理，最终得到归一化矩阵Sij.

所有被评价的各项指标的无量纲处理结果组成为矩阵S.

Step3 计算指标的客观权重.

1）计算i项指标的熵值

2）计算i项指标的权重

Step4 计算指标的组合权重.

本文提出将G1法获取的主权权重wi与熵权法获取的客观权重ui进行组合优化，是指标体系兼具主观权重与客观权重的优点，使最终得到的评价结果更加符合实际情况，组合权重的计算公式如下：

式中：α为主观权重系数；β 为客观权重系数；α与β 的乘积大于0，α与β 之和等于0，且α与β 值的区间为［0，1］.某地j的主客观加权属性值一致水平公式为：

式中：αviχij为主观加权属性值；βuixij为客观加权属性值. 为了使主观、客观加权属性值的一致水平趋于最小化，采用公式（11）进行线性加权来优化模型：

式中：α与β 的乘积大于0，α与β 之和等于0，且α 与β 值的区间为［0，1］.

公式（11）中关于α与β 的二元优化模型采用拉格朗日乘法，最终求得的指标权重系数值带入公式（12），从而获得组合权重λi. 设λ为所有评价指标的权重组成的权重向量，则

Step5 基于不确定性的高速公路路线方案安全比选方法.

将各指标进行无量纲处理后，将公式（12）的组合权重向量的转置解和标准化矩阵S带入到高速公路路线方案安全比选的计算公式，得到各比选方案的评价结果H，公式（13）即为基于云模型的G1-熵权高速公路路线方案安全比选模型.式中：H即为各方案的综合比选结果，H值越大，表明方案整体安全性更好，方案越优；反之，则表明方案越差.

4 实例分析

结合西南地区某高速公路进行方案比选实例分析，对该高速公路进行评价时需要考虑众多的定性指标，主要研究了K线方案（方案一）、K+B9线（方案二）、B6+C1线方案（方案三），三个同深度方案的路线走向示意图如图2所示.

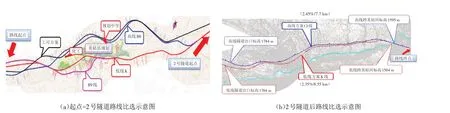
图2 路线走向示意图Fig.2 Schematic diagram of the route

通过对该段线路工程概况的整理，得出上述3 个方案各指标取值的基础数据，并聘请专家采用语言类模糊数对定性指标进行赋值，见表5. 下面说明本文模型的计算式.

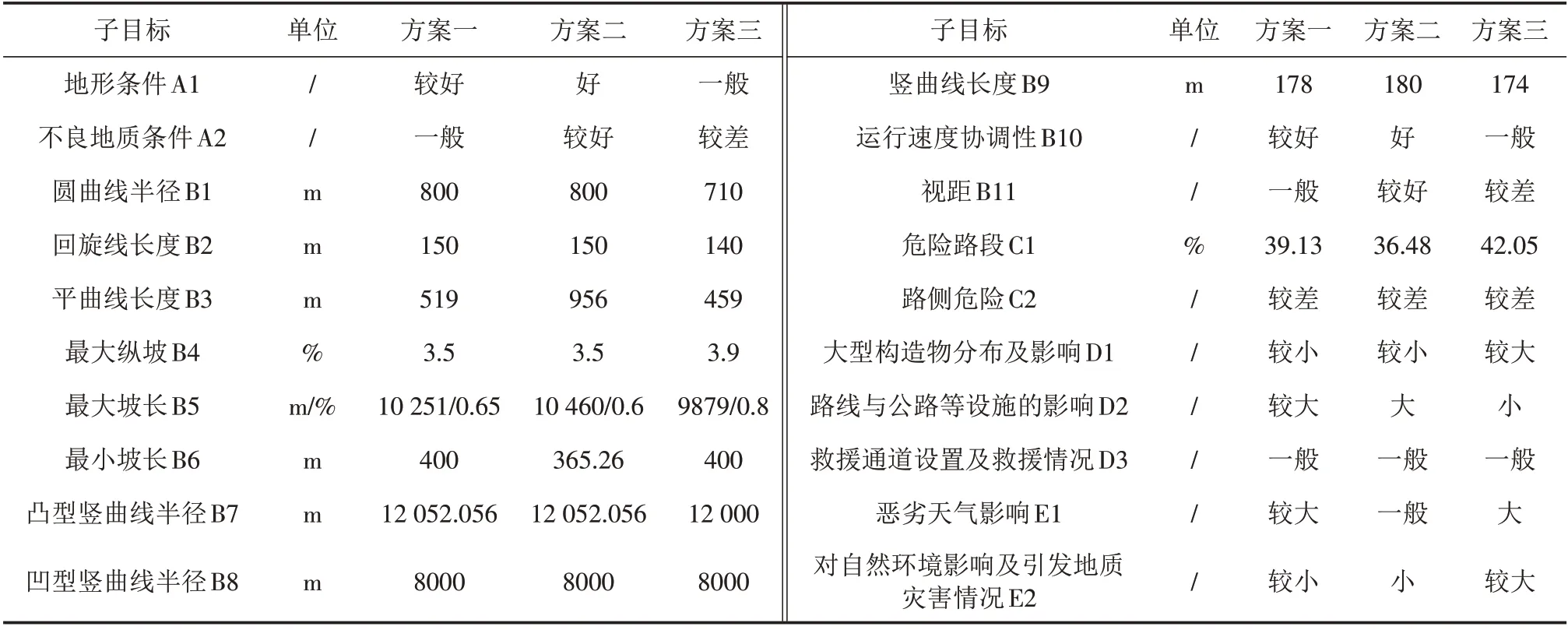
表5 各比选方案对应指标取值Tab.5 Corresponding indicators for each comparison scheme

1）G1 法计算主观权重. 通过上文所提计算方法，并根据每位专家的调查反馈结果计算相应的一级指标、二级指标的权重，并计算每位专家的权重指数，对赋权的结果进行整理，计算得到高速公路路线方案安全比选的一级指标、二级指标的单层权重及综合权重，综合权重为（0.035 1，0.056 1，0.018 6，0.015 5，0.012 9，0.022 4，0.018 6，0.015 5，0.007 7，0.010 8，0.006 4，0.050 1，0.031 3，0.243，0.141 8，0.081 5，0.042 5，0.051，0.093 7，0.052 1）.

2）熵权法计算客观权重. 通过表5的取值，按照2.2章节中关于云模型的计算方法对表5中的定性指标进行，计算结果见表6.

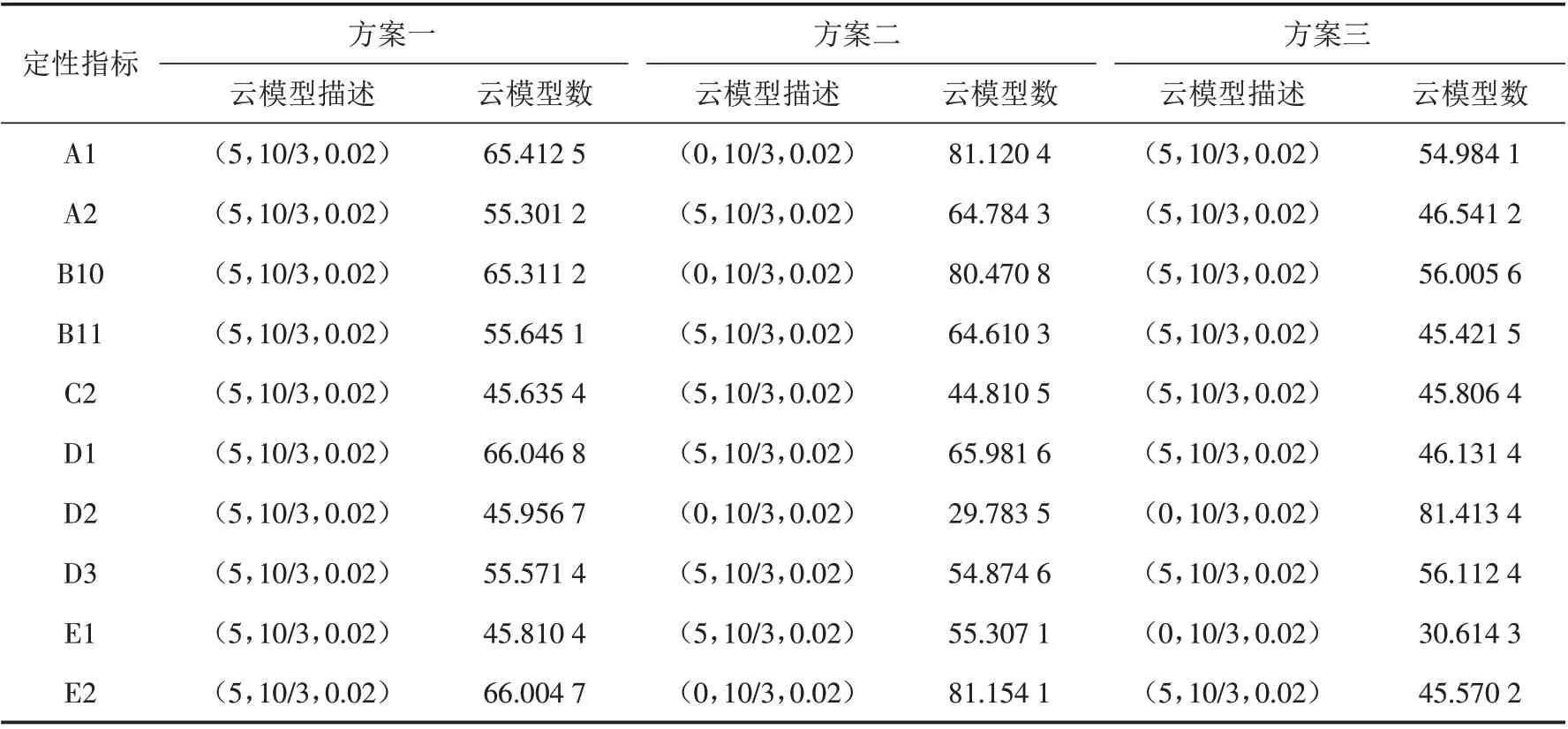
表6 定性指标得分Tab.6 Qualitative indicator scores

根据公式（7）、（8）计算出指标的客观权重：

（0.024 3，0.099 7，0.031 3，0.004 1，0.007 8，0.048 9，0.021 4，0.007 8，0.016 8，0.017 4，0.004 2，0.078 4，0.028 6，0.187 4，0.074 5，0.051 1，0.103 6，0.027 4，0.123 6，0.041 7）.

根据公式（12）得到指标体系的组合权重：

（0.030 2，0.077 8，0.025 0，0.010 1，0.010 5，0.035 5，0.020 1，0.011 9，0.012 2，0.014 1，0.005 4，0.064 3，0.030 3，0.218 1，0.110 3，0.067 4，0.072 6，0.040 0，0.109 1，0.047 5）.

3）综合比选结果分析. 将计算出的组合权重与规范化矩阵的结果带入公式（13），即可得出三个方案的综合评价得分，最终算出的3个同深度比选方案的综合评价分数见表7.

表7 方案综合得分Tab.7 Eme comprehensive score

通过不确定性分析的高速公路路线比选方法，最终确定的最优方案为方案二（K+B9线），方案一（K线方案）为第二选择方案，方案三（B6+C1线方案）为第三选择方案，这与工程实际比选结果是一致的.

从表7中可以看出，基于不确定性分析的高速公路路线方案安全比选方法与工程实际比选结果相比，不仅能给出安全性最优的方案，还能根据各方案最终计算分值结果给出第二推荐方案、第三推荐方案，通过分值大小可以看出各方案间的差距. 同时实现方案中定性指标的有效量化及各指标权重的赋值，能够根据量化的定性指标及权重赋值找出造成方案安全性差距的原因，有针对性地进行改善及优化.

5 结语

1）本文针对评价体系中的定性指标，根据云模型理论在定性和定量间的不确定性转换，通过专家的语言变量对定性指标进行评价，实现了对定性指标的有效量化.

2）根据所建立的指标体系的特点，采用组合赋权方法进行指标权重的确定，即采用G1 法确定主观权重，在利用云模型将定性指标转换为定量描述后采用熵权法求取客观权重，并通过相应的系数求得组合权重值，该方法既包含专家的经验，也体现了指标自身携带的信息.

3）根据高速公路路线方案比选的特点，建立了基于不确定性的高速公路路线方案比选方法. 该方法克服了传统评价方法的缺点，充分考虑了定性指标的不确定性特征，实现了定性指标的定量化研究以及定量指标和定性指标的综合比选. 最后通过西南某高速公路路线方案比选实例说明了方法的可行性和实用性.

但本文仍存在以下不足：目前对于高速公路建设与工程技术指标、投资、环境影响等研究较多，而对于高速公路建设与安全的影响则停留在初级阶段. 本文建立的评价指标体系只考虑了其中地形地质条件、线形协调性和设计要素、危险路段和路侧危险、路网布局和大型构造物分布、恶劣天气影响因素，后续研究中应对指标的安全性进行全面分析；对于云模型理论在方案比选中的应用需进一步完善，使其可以在不同等级的公路中进行方案比选，同时为了实现方案比选的自动化，应开发出相应的方案比选系统.