航天器狭小空间总装紧固件预紧技术研究

宋晓晖，刘智斌，薛 峰，顾 磊

（1. 北京卫星环境工程研究所，北京 100094；2. 北京市航天产品智能装配技术与装备工程技术中心，北京 100094）

螺纹连接结构作为航天器产品大量使用的基本结构，直接影响到航天器整体性能，甚至会直接关系到航天器飞行任务的成败。美国第1颗WGS（World Geodetic System）卫星在2005年组装时，有148个紧固件安装不当（每颗卫星上有1500多套紧固件），因而需要重新组装，并由波音公司负责紧固件的检查费用，同时另外2颗WGS卫星也要进行检查。螺纹连接的可靠性成为航天器研制过程中关注的焦点。

国内卫星上的螺纹连接形式一般是通过钛螺钉与结构板（如铝蒙皮蜂窝板、碳纤维蒙皮蜂窝板）内的钢丝螺套连接。为保证螺纹连接的高可靠性，确保满足力学环境要求，一般采用对螺纹紧固件施加预紧力的方法进行紧固。对螺纹紧固件预紧力的控制一般采用力矩控制法，即采用扭矩拧紧装置通过操纵拧紧力矩值T的方式来控制螺纹连接的预紧力F。

扭矩拧紧装置在航天器总体装配中扮演着重要角色。特别是在长寿命、高可靠航天器的高质量研制背景下，扭矩拧紧装置成为机械连接中必不可少的在线检测和装配设备，对保证航天器的装配质量起到关键作用。航天器总装研制中使用的扭矩拧紧装置一般为预置式力矩扳手，尤其是手动预置式力矩扳手应用尤其普遍。目前常用的手动预置式力矩扳手型号有GEDORE DREMOMETER 753型、GEDORE DREMOMETER 8560型等。

尽管预置式力矩扳手在航天器研制过程中发挥了很大的积极作用，满足了大部分工况下紧固件预紧力的加载需求，但随着航天器结构日益复杂，由于操作空间的限制导致的紧固件无法实施力矩拧紧的情况日趋增多。如果紧固件的预紧力未达到设计指标要求，则可能导致螺钉脱落、螺钉断裂等故障[1]，致使航天器研制质量受到影响。

在航天器总装研制过程中，对紧固件进行扭矩加载是控制螺纹拧紧程度的主要手段。由于航天器结构设计日趋复杂，受到操作空间限制，扭矩拧紧工具无法在该空间内进行正常作业，紧固件无法使用标准工具实施扭矩加载的问题越来越多。经过分析，可将问题主要归纳为两种情况，一种是紧固件轴向空间受到限制，即螺钉轴线方向上的空余有效高度小于力矩扳手及转接头的高度之和，力矩扳手无法与螺钉实施有效连接。另一种是紧固件径向空间受到限制， 即螺钉直径方向上的空余有效空间小于力矩扳手头部的回转直径，力矩扳手无法与螺钉进行有效连接。

本文在分析航天器紧固件无法实施扭矩加载工况的基础上，提出了一整套基于一体式L型杆的航天器狭小空间内紧固件螺钉预紧解决方案，有效解决了恶劣工况下对螺钉施加预紧力的难题。

1 螺纹预紧机理

在紧固件安装过程中，螺钉的拧紧力矩通过螺纹副的相对运动转化成从轴向压紧螺纹的预紧力，螺纹连接的可靠性主要取决于紧固件与基体之间发生的预紧力[2]，预紧力的主要形式是拉力。拧紧力矩和预紧力之间存在对应关系，在紧固件、被连接件和基体状态确定的情况下，一般而言，加载在螺钉上的拧紧力矩越大，预紧力相应越大，相应螺纹拧紧程度越高，螺纹连接越可靠。螺钉拧紧力矩T与轴向预紧力F存在以下关系[3]：

其中，K为拧紧力矩系数；d为螺纹公称直径。

在螺钉同等规格的情况下，螺钉的拧紧力矩受到两个因素影响：合理的预紧力和拧紧系数。

拧紧力矩系数K的理论公式：

其中，φ为螺纹升角，φ=arctan(p/πd2)；ρ为螺纹连接副的当量摩擦角，通常φ=arctan1.15f；f为螺纹副摩擦系数；d2为螺纹中径；μn为螺钉与被连接件支撑面间的组合摩擦系数；rn为圆环面当量摩擦半径，。

在航天器总体设计过程中，紧固件的规格是预先设计的，因此螺钉的公称直径d为确定值。螺钉的拧紧系数K主要受螺钉与被连接件螺纹副之间的摩擦和螺钉头部与被连接件表面之间的摩擦影响[4]。

航天器一般采用内六角形式的钛螺钉，基体一般是铝蒙皮蜂窝结构板，被连接材料一般为铝合金板。在螺钉、基体和被连接件状态均确定的情况下，相应的拧紧系数K应为一定值。航天器上典型的螺纹连接方式如图1所示。图2是航天器上典型的螺钉安装过程中扭拉关系曲线[5]，其中紧固件规格为M3，采用强度等级为880MPa的ML30CrMnSiA材质，基体材料为1Cr18Ni9Ti的不锈钢，被连接件为牌号5A06的铝材。

可知，紧固件进行力矩加载后产生的抗拉力与预置的扭矩之间的关系基本成线性，也就是说只要合理地对螺钉施加安装扭矩就能实现紧固件预紧力控制，从而保证紧固件安装牢靠，进而确保被连接件的安装可靠性。

2 方案设计及分析

对于因轴向、径向空间受限造成的紧固件无法实施扭矩拧紧的原因可以归结为力矩扳手（包含转接杆）头部过大，不能在目标紧固件空余空间内进行有效运动，在操作空间无法改变的前提情况下，解决渠道只能是将力矩扳手头部尽量变小，以适应操作空间需要。

图1 螺纹连接示意图Fig.1 Sketch of screw installation

图2 螺钉安装扭拉关系曲线Fig.2 Pull-up curve of screw installation

对于轴向空间受限制的情况，应将扳手头部连同与螺钉连接的垂直转接杆尽量变短，以适应有限的轴向操作空间。

对于径向空间受限制的情况，应将扳手头部直径沿径向缩小或者将扳手头部沿径向后退至不占用有效操作空间的位置。

目前在航天器总装过程中常用的力矩扳手，例如GEDORE DREMOMETER 753型，其头部高度约为50mm，头部半径约为15mm，极大地占用了操作空间。根据对航天器总装紧固件的调研，航天器紧固件实施力矩加载的轴向空间最少值约16mm、径向空间最小值约10mm，现有的力矩扳手无法满足需求。

GEDORE4400型力矩扳手与普通力矩扳手结构形式不同，其力矩输出部位可以远离与紧固件连接的部位，可以与L型连接杆组合从而实现狭小空间内紧固件力矩加载。一体式L型连接杆具有较好的刚性，且可根据需要定制不同的长度，以适应轴向、径向空间需要。转接杆与力矩扳手采用过渡配合，能够最大限度减少配合引起的系统误差。图3是GEDORE4400型力矩扳手与一体式L型转接杆组合后与内六角螺钉连接的示意图。

2.1 L型杆设计

某种意义上来说，力矩扳手转接工装实际上就是连接需紧固的螺钉与力矩扳手的工具，其目的是通过转接获得有效的连接及操作空间，从而有效地控制紧固件的拧紧力矩[6]。

按照系列化、模块化、参数化的设计原则，与GEDORE4400型力矩扳手连接的转接杆设计为一体式L型结构，可分为水平杆和垂直杆两部分，垂直杆与水平杆采用一体式连接设计，以减少转接环节引入的误差，其中垂直杆用于与目标紧固件连接，水平杆用于与力矩扳手连接。

一体式L型转接杆构型示意如图4所示，设定垂直杆有效长度为l1，水平杆有效长度为l2，水平杆后部的连接套根据力矩扳手形式设计为φ15mm圆柱形，水平杆与连接套通过锁定螺丝固连在一起，L型杆截面形状为正六边形，与对应的内六角螺钉端头匹配。通过对转接杆截面规格及l1、l2长度分别进行不同的组合，研制一套转接杆，以满足不同工况需要。

图3 力矩扳手及L型杆组合与螺钉连接示意图Fig.3 Sketch of the combination of one-piece L-shaped connecting rod joint with screw

在航天器研制中，L型杆截面形状可适应M3、M4、M5、M6、M8等内六角圆柱头螺钉，垂直杆长度包括15mm、20mm、30mm、50mm共4个规格，水平杆长度包括50mm、80mm、100mmm、120mm共4个规格。

2.2 L型杆有限元分析

L型转接杆的材料为T9工具钢，采用一次成形加工而来。工具钢是用来制造耐磨工具的钢，具有较高的硬度和适当的韧性。使用ANSYS Workbench软件对L型杆进行力学仿真计算，其中水平杆长度设置为最大值150mm，M4螺钉拧紧力矩取设计要求的最大值2.5N·m时，将集中载荷施加在垂直杆末端，得出应力分布如图5所示。应力最大区域出现在水平杆与垂直杆结合部位，应力最大值为870Pa，远低于该工具钢的屈服强度240MPa。因此不会出现材料破坏的情况，强度能够满足力矩加载要求。

3 试验验证

由于一体式L型杆与力矩扳手组合后，相当于改变了力臂长度，而且由于系统误差的存在，会造成理论力矩传递系数与实际力矩传递系数之间有偏差。为了得出对应于每个L型杆的真实力矩传递系数，设计了扭矩加载工具组合的标定试验，并分析力矩扳手加转接杆系统输出力矩与力矩扳手输入值、转接杆长度等参数的关系，得出扭矩加载工具力矩传递系数。

图4 一体式L型杆构型示意Fig.4 Sketch of one-piece L-shaped transfer

图5 一体式L型杆应力云图Fig.5 Stress diagram of L-shaped

3.1 试验方案

本次试验的设备主要为8624–001型扭矩测试仪，测试精度0.001N·m，试验对象主要包括力矩扳手、一体式L型转接杆。试验过程中，操作者采用钳夹方式把握力矩扳手，以最大限度地减少人为误差和随机误差，而且保证垂直杆尽量与力矩标定仪转接头垂直，操作过程中缓慢、平稳实施加力。

3.2 传递系数分析

图6为力矩扳手与一体式L型转接杆连接关系的简化示意图。其中：线段AB表示水平杆，有效长度为l；线段BC表示力矩扳手的施力力臂，点D表示操作者使用力矩扳手时的施力点，线段BD表示力矩扳手施力点到方榫中心线的距离，有效长度为l；α表示水平杆与力矩扳手手柄之间的夹角；F表示从点D处施加的垂直于线段BC的力。

在力矩扳手加转接工装系统处于静力学平衡的前提下，对外力F施加给点A的力矩M'以及施加给力矩扳手（即点B）M之间的关系进行了推导。

可知，力矩扳手加转接工装系统力矩输出值M'与力矩扳手力矩输入值M之间的关系取决于力矩转接工装水平杆的长度l'、力矩扳手施力力臂的长度l以及水平杆与力矩扳手施力臂之间的夹角α。计算传递系数K时，先测量转接工装水平杆的有效长度以及待使用的力矩扳手的有效长度，并根据公式（7）计算给出理论上的传递系数K。

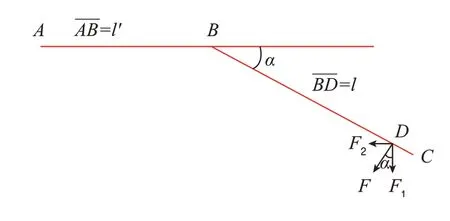
图6 力矩扳手与L型杆组合系统受力分析示意Fig.6 Stress analysis diagram of torque spanner plus one-piece L shaped

3.3 试验过程

采用不同长度的垂直杆分别进行适应，发现垂直杆的长度变化对力矩输出值基本无影响。在输入力矩一定的情况下，影响力矩输出值变化的主要因素是水平杆的长度，水平杆长度直接决定了扭矩传递系数K。

将试验中不同水平杆长度的试验数据罗列如表1所示。表1还给出了M4螺钉的扭矩传递系数K的试验测量值和理论值比对，可知力矩扳手加一体式L型转接工装系统的输出力矩实测值基本上在理论计算值的88%～98%之间。造成误差的主要原因包括两个方面，其一是水平杆自身的刚度，随着水平杆长度的增加，金属杆在力矩施加过程中会产生一定的弹性变形，造成有效长度l'的变化；其次是力矩扳手和水平杆二者之间的同轴度，二者之间的α越大，输出力矩的误差也随之增大。对表1的数据比对、分析，考虑到系统误差，可以认为一体式L型转接工装的力矩传递系数在合理可控的范围内[7]。

3.4 结果分析与讨论

对比表1中的试验数据和理论数据可知，使用一体式L型转接杆的理论传递系数与标定试验得出的实际传递系数存在一定误差，影响传递系数误差的主要因素在于使用转接工装后至少增加1个转接环节，且力矩扳手与转接工装间的配合引入的摩擦将带来一定的系统误差，而且水平杆与力矩扳手存在不确定的夹角误差也会引入到传递系数系统误差里。

为了减少输出力矩的偏差，保证K值的准确性，应在设计及实施过程中采取如下措施：

（1）尽量减小水平杆有效长度l'与力矩扳手力臂长度l之比，即在满足要求的前提下，选用l'与l之比较小的一体式L型转接工装加力矩扳手组合。

（2）为减少测量过程中产生的误差对K值的影响，可尽量使力矩扳手和水平杆在一条直线上，即α=0，则该工况下的力矩传递系数计算公式可简化为。

4 结论

对于因轴向空间受限而引起的无法使用标准力矩扳手实施紧固件扭矩加载的问题，可以根据紧固件端头轴向空间的大小选取所需要的一体式L型转接工装垂直杆的长度，与一定长度的水平杆结合，可以实现紧固件力矩加载。根据对各型号的调研，轴向空间最小值确定为16mm，故将垂直杆的长度最小值定义为15mm，能够满足型号总装研制需要。对于紧固件径向空间受限而引起的无法使用标准扳手实施紧固件扭矩加载的问题，该一体式L型杆采用与紧固件相同的正六边形，不会凸出在螺钉径向包络，能够满足总装作业需求需要。

表1 M4螺钉扭矩测量记录表Table 1 Log sheet of torque about M4 bolt

基于一体式L型杆的航天器狭小空间内紧固件预紧技术， 解决了航天器总装过程中紧固件轴向、径向空间受限工况下的力矩加载难题，合理地控制了系统误差，具有通用性强、灵活性好的特点。通过理论计算和试验验证了该方案的工程应用效果，在有效提高紧固件安装可靠性的基础上，满足了长寿命、高可靠性航天器研制需求，具有良好的推广应用前景。