2020年美国数学竞赛(AMC10B)的试题与解答

华南师范大学数学科学学院(510631) 李湖南

1.What is the value of 1-(-2)-3-(-4)-5-(-6)?

(A)-20 (B)-3 (C) 3 (D) 5 (E) 21

译文式子1-(-2)-3-(-4)-5-(-6)的值是多少?

解直接计算,原式=1+2-3+4-5+6=5,故(D)正确.

2.Carl has 5 cubes having side length 1,and Kate has 5 cubes each having side length 2.What is the total volume of the 10 cubes?

(A) 24 (B) 25 (C) 28 (D) 40 (E) 45

译文卡尔有5 个棱长为1 的立方体,凯特有5 个棱长为2 的立方体.则这10 个立方体的总体积是多少?

解依题意,总体积=5×13+5×23=45,故(E)正确.

3.The ratio ofwtoxis 4:3,the ratio ofytozis 3:2,and the ratio ofztoxis 1:6.What is the ratio ofwtoy?

(A) 4:3 (B) 3:2 (C) 8:3 (D) 4:1 (E) 16:3

译文已知w与x之比为4:3,y与z之比为3:2,z与x之比为1:6.则w与y之比是多少?

解化简即得故(E)正确.

4.The acute angles of a right triangle area°andb°,wherea＞band bothaandbare prime numbers.What is the least possible value ofb?

(A) 2 (B) 3 (C) 5 (D) 7 (E) 11

译文一个直角三角形的两个锐角分别是a°和b°,其中a＞b且a和b均为素数.则b最小可能的值是多少?

解问题转化为求a+b=90 的最小素数解,可解得a=83,b=7,故(D)正确.

5.How many distinguishable arrangements are there of 1 brown tile,1 purple tile,2 green tiles,and 3 yellow tiles in a row from left to right? (Tiles of the same color are indistinguishable)

(A) 210 (B) 420 (C) 630 (D) 840 (E) 1050

译文把1 块棕色瓷砖,1 块紫色瓷砖,2 块绿色瓷砖和3 块黄色瓷砖从左到右排成一行有多少种不同的方法? (同种颜色的瓷砖不可分辨)

解这是一个组合问题,相当于从7 块瓷砖中选出1 块棕色的,再选出1 块紫色的,然后选出2 块绿色的,剩下的全是黄色,即有=7×6×10×1=420 种方法,故(B)正确.

6.Driving along a highway,Megan noticed that her odometer showed 15951(miles).This number is a palindrome—it reads the same forward and backward.Then 2 hours later,the odometer displayed the next higher palindrome.What was her average speed,in miles per hour,during this 2-hour period?

(A) 50 (B) 55 (C) 60 (D) 65 (E) 70

译文梅根正开车在一条高速公路上,她注意到里程表正好显示着15951 英里.这是一个回文数—正反读起来是一样的.2 个小时后,里程表显示着下一个更大的回文数.则在这2 小时期间她的平均速度是多少英里/小时?

解下一个回文数是16061,在2 小时内,梅根行驶了16061-15951=110 英里,从而她的平均速度是55 英里/小时,故(B)正确.

7.How many positive even multiples of 3 less than 2020 are perfect squares?

(A) 7 (B) 8 (C) 9 (D) 10 (E) 12

译文有多少个小于2020 的平方数是正的3 的偶数倍?

解依题意,正的3 的偶数倍的平方数必须是62的倍数,因此满足条件的数有以下这些:62,122,182,242,302,362,422,共7 个,故(A)正确.

经过上述的分析，不难发现：传统的IoT技术和中心化的系统框架已经很难满足未来的发展需求。针对IoT平台的特点，区块链技术能解决大量的智能设备数据在中心化的系统框架中会出现的安全和管理问题。区块链是一种集成分布式数据库、共识机制、点对点（P2P）传输和非对称加密算法等新型应用模式，具有去中心化、开放性、自治性、匿名性和信息不可篡改的特点。本文主要对IoT平台之一的体域网展开了详细研究，结合新兴的区块链技术，针对传输的安全性能和数据传输性能差的特点，研究分析了适用于体域网的身份认证技术，利用区块链技术在体域网平台下设计一个新兴的系统框架，主要解决以下问题:

8.PointsPandQlie on the number line withPQ=8.How many locations for pointRin this plane are there such triangle with verticesP,Q,andRis a right triangle with area 12 square units?

(A) 2 (B) 4 (C) 6 (D) 8 (E) 10

译文点P,Q在数轴上,PQ=8.在平面上有多少个点R使得以P,Q,R为顶点的直角三角形面积为12 个平方单位?

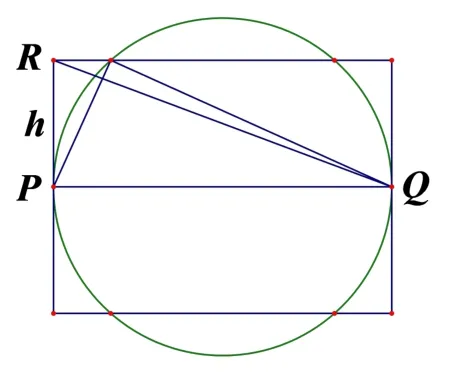
解以PQ为底,则ΔPQR的高为h=12×2÷8=3,从而点R在与PQ距离为3 的平行线上.如图示,作距离为3 的上下两条平行线,分三种情况:(1)若∠RPQ为直角,则R在过点P且垂直于PQ的直线与平行线的交点上,共2 个点;(2)若∠RQP为直角,则R在过点Q且垂直于PQ的直线与平行线的交点上,共2 个点;(3)若∠PRQ为直角,则R在以PQ为直径的圆与平行线的交点上,共4 个点.故满足条件的点R有8 个,(D)正确.

9.How many ordered pairs of integers(x,y)satisfy the equationx2020+y2=2y?

(A) 1 (B) 2 (C) 3 (D) 4 (E) infinitely many

译文有多少个整数对(x,y)满足方程x2020+y2=2y?

解原方程可化为x2020+(y-1)2=1,容易解得故满足方程的解共有4 对,(D)正确.

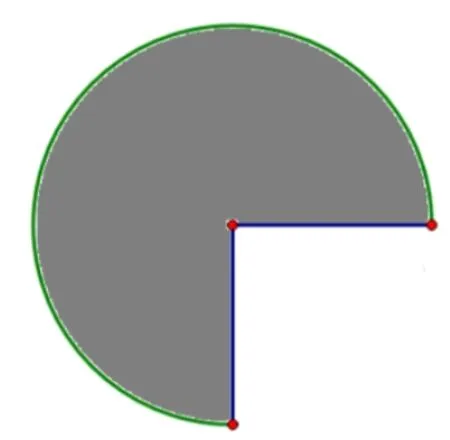
10.A three-quarter sector of a circle of radius 4 inches together with its interior can be rolled up to form the lateral surface of a right circular cone by taping together along the two radii shown.What is the volume of the cone in cubic inches?

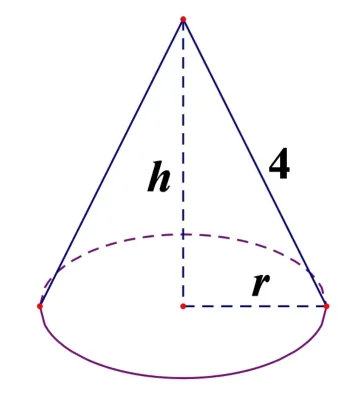
译文如图示,有一个半径为4 英寸的圆的四分之三部分连同它的内部,将其沿着两条半径粘合,正好可以卷成一个圆锥的侧面.则这个圆锥的体积是多少立方英寸?

解设这个圆锥的底面半径和高分别为r和h,则有2πr=·2π·4,r2+h2=42,解得r=3,h=于是该圆锥的体积为V==故(C)正确.

11.Ms.Carr asks her students to read any 5 of the 10 books on a reading list.Harold randomly selects 5 books from this list,and Betty does the same.What is the probability that there are exactly 2 books that they both select?

译文卡尔夫人要求她的学生们从一个含有10 本书的书单中阅读其中的5 本.哈罗德从书单中随机选择了5 本书,贝蒂也随机选择了5 本书.那么他们同时选择了其中2 本书的概率是多少?

解假定哈罗德选择的5 本书为A,B,C,D,E,则符合条件的结果是贝蒂从中选择了任意2 本,且在另外5 本书中选择了任意3 本,即有=100 种选择,概率为故(D)正确.

12.The decimal representation ofconsists of a string of zeros after the decimal point,followed by a 9 and then several more digits.How many zeros are in that initial string of zeros after the decimal point?

(A) 23 (B) 24 (C) 25 (D) 26 (E) 27

译文的小数表示为小数点后面一串的0,接下来是9 和其它几位数字.则在小数点后面那一串有多少个0?

解又因此,的小数表示中,小数点后面有26 个0,故(D)正确.

13.Andy the Ant lives on a coordinate plane and is currently at (-20,20) facing east (that is,in the positivex-direction).Andy moves 1 unit and then turns 90°degrees left.From there,Andy moves 2 units (north) and the turns 90°degrees left.He then moves 3 units(west)and again turns 90°degrees left.Andy continues his progress,increasing his distance each time by 1 unit and always turning left.What is the location of the point at which Andy makes the 2020th left turn?

(A)(-1030,-994) (B)(-1030,-990) (C)(-1026,-994)(D)(-1026,-990) (E)(-1022,-994)

译文蚂蚁安迪住在坐标平面上,且在点(-20,20)处面朝东(即x轴正方向).安迪爬了1 个单位然后向左转90°,跟着安迪爬了2 个单位(向北)然后向左转90°,接着他又爬了3 个单位(向西)然后向左转90°.安迪重复他这种动作,每次都比上次多爬1 个单位然后向左转.则安迪向左转了2020次之后处在什么位置?

解从方向上来讲,安迪爬4 次就是一个周期.他的爬行轨迹为:由此可见,每爬一个周期,安迪会向西移动2 个单位,向南移动2 个单位.于是,经过2020 次爬行即505 个周期之后,安迪所处的位置为(-20-505×2,20-505×2) 即(-1030,-990),故(B)正确.

14.As shown in the figure below,six semicircles lie in the interior of a regular hexagon with side length 2 so that the diameters of the semicircles coincide with the sides of the hexagon.What is the area of the shaded region—inside the hexagon but outside all of the semicircles?

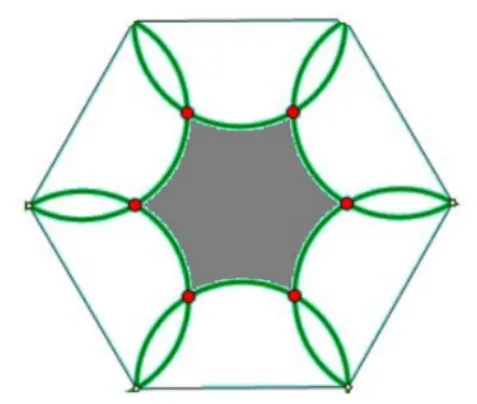
译文如图所示,一个边长为2 的正六边形的内部有6个半圆,这些半圆的直径恰好是该六边形的6 条边.则图中阴影部分——六边形内部半圆以外的面积是多少?

解S六边形=6·S半圆+S阴影-6·S树叶,其中树叶为两个半圆的交集部分.而S半圆=树叶恰好是半圆内一个60°的扇形去掉一个正三角形的部分的两倍,于是有

故(D)正确.

15.Steve wrote the digits 1,2,3,4,and 5 in order repeatedly from left to right,forming a list of 10,000 digits,beginning 123451234512….He then erased every third digit from his list(that is,the 3rd,6th,9th,…digits from the left),then erased every fourth digit from the resulting list(that is,the 4th,8th,12th,…digits from the left in what remained),and then erased every fifth digit from what remained at that point.What is the sum of the three digits that were then in the positions 2019,2020,2021?

(A) 7 (B) 9 (C) 10 (D) 11 (E) 12

译文史蒂夫从左至右依次按顺序地重复写下数字1,2,3,4,5,形成了一个以123451234512…开头的10,000 位数字.然后他每三位擦掉最后一位数(也就是从左边开始的第3 位,第6 位,第9 位,…),接着他在剩下的数字中每四位擦掉最后一位数(也就是剩下从左边开始的第4 位,第8 位,第12 位,…),最后他在剩下的数字中每五位擦掉最后一位数.则在剩下的数字中第2019,2020 和2021 位数字之和是多少?

解我们可选择30 位数字为一个周期进行分析:123451234512345123451234512345,第一次操作后得12452351341245235134,第二次操作后得124235341452513,第三次操作后得124253415251,剩下12 位数字.而2019≡3(mod 12),即剩下数字中的第2019,2020 和2021 位数字就是最后12 位数字中的第3,4,5 位,和为11,故(D)正确.

16.Bela and Jenn play the following game on the closed interval[0,n]of the real number line,wherenis a fixed integer greater than 4.They take turns playing,with Bela going first.At his first turn,Bela chooses any real number in the[0,n].Thereafter,the player whose turn it is chooses a real number that is more than one unit away from all numbers previously chosen by either player.A player unable to choose such a number loses.Using optimal strategy,which player will win the game?

(A) Bela will always win.

(B) Jenn will always win.

(C) Bela will win if and only ifnis odd.

(D) Jenn will win if and only ifnis odd.

(E) Jenn will win if and only ifn＞8.

译文贝拉和珍在实数轴的闭区间[0,n]上玩如下游戏,其中给定整数n＞4.他们轮流玩,贝拉先开始.最开始,贝拉在[0,n]上选择一个任意实数.然后,接下来轮到的选手要选择一个与他们之前选择的所有实数距离都要大1 个单位的实数.无法选择的选手就算输.使用最优策略,哪位选手会赢得这个游戏?

解贝拉将赢得这个游戏.因为最开始贝拉选择将区间分成两个对称的小区间和接下来无论珍在哪个区间中选择什么数,贝拉都将选择另一个区间中关于中心对称的那个数.只要珍能够选择数,贝拉就可以继续游戏.到最后,无法选择的一定是珍,即珍必败,故(A)正确.

17.There are 10 people standing equally spaced around a circle.Each person knows exactly 3 of the other 9 people:the 2 people standing next to her or him,as well as the person directly across the circle.How many ways are there for the 10 people to split up into 5 pairs so that the members of each pair know each other?

(A) 11 (B) 12 (C) 13 (D) 14 (E) 15

译文10 个人等距地围坐在一个圆周上,每个人都只认识其余9 人中的3 人:与他或她相邻的2 人,以及圆周上相对的那个人.问有多少种方式把这10 个人分成5 对,使得每对的两个人都互相认识?

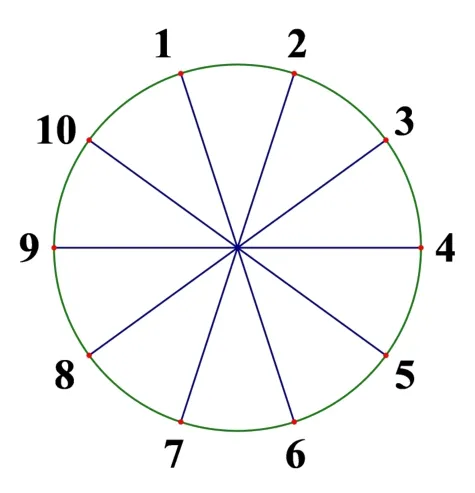
解如图示,分别给这10 个人编号为1,2,3,…,10,互相认识的人用线段或弧线连接,先考虑1 号,分如下三种情况:

(1)1 与2 配对:若3 与4 配对,则有{5,6},{7,8},{9,10},或{5,10},{6,7},{8,9},共2 种方式;若3 与8 配对,则7 必与6 配对,有{4,5},{9,10},或{4,9},{5,10},也是2 种方式.

(2)1 与10 配对:同理可得4 种方式;

(3)1 与6 配对:若2 与3 配对,则7 必与8 配对,有{4,5},{9,10},或{4,9},{5,10},共2 种方式;若2 与7 配对,则有{3,4},{5,10},{8,9},或{3,8},{4,5},{9,10},或{3,8},{4,9},{5,10},共3 种方式.

综上可得,符合条件的分法共有13 种.故(C)正确.

18.An urn contains one red ball and one blue ball.A box of extra red and blue balls lies nearby.George performs the following operation four times:he draws a ball from the urn at random and that takes a ball of the same color from the box and returns those two matching balls to the urn.After the four iterations the urn contains six balls.What is the probability that the urn contains three balls of each color?

译文缸里有1 个红球和1 个蓝球,旁边另有一盒子红球和蓝球.乔治进行如下操作四次:首先他从缸里随机拿起一个球,然后他从盒子里拿起一个相同颜色的球,接着把两个球放回缸里.四次操作之后,缸里有6 个球.则缸里有两种颜色各3 个球的概率是多少?

解四次操作之后,缸里可能有1,2,3,4,5 个红球.根据对称性,剩1 个红球和1 个蓝球即5 个红球的概率是一样的,2 个红球和4 个红球的概率是一样的.

剩1 个红球,也即乔治每次拿起的都是蓝球,从而P(1个红球)=

剩2 个红球,也即乔治四次操作中只拿起一次红球,其中第1,2,3,4 次均有可能,从而

因 此,P(3个红球)=1-2× P(1个红球)-2×P(2个红球)=故(B)正确.

19.In a certain card game,a player is dealt a hand of 10 cards from a deck of 52 distinct cards.The number of distinct(unordered) hands that can be dealt to the player can be written as 158A00A4AA0.What is the digitA?

(A) 2 (B) 3 (C) 4 (D) 6 (E) 7

译文在某扑克游戏中,一位选手要从装有52 张不同扑克的盒子中抽取一手10 张牌.抽取这一手牌(无序)的方式可以写成158A00A4AA0 种,则数字A是多少?

解从52 张牌中抽取10 张牌的方式为种,而==15820024220,故A=2,(A)正确.

20.LetBbe a right rectangular prism (box) with edges lengths 1,3,and 4,together with its interior.For realr＞0,letS(r)be the set of points in 3-dimensional space that lie within a distancerof some pointB.The volume ofS(r) can be expressed asar3+br2+cr+d,wherea,b,c,dare positive real numbers.What is

(A) 6 (B) 19 (C) 24 (D) 26 (E) 38

译文设B是一个棱长分别为1,3,4 的长方体.对于实数r＞0,令S(r)为三维空间中与B中的点距离为r的所有点的集合,S(r)的体积可以表示成ar3+br2+cr+d,其中a,b,c,d均为正实数.则是多少?

解实际上,S(r)就是长方体往外扩张距离为r的所有内部点集,平面往外扩张形成一个高为r的长方体,棱往外扩张形成个底面半径为r的圆柱体,点往外扩张形成个半径为r的球体,从而

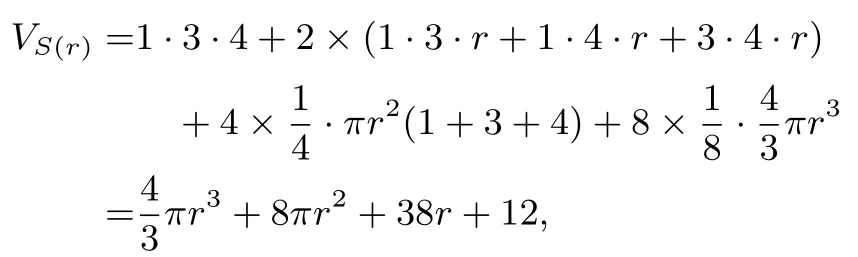
于是有a=b=8π,c=38,d=12.故==19,(B)正确.

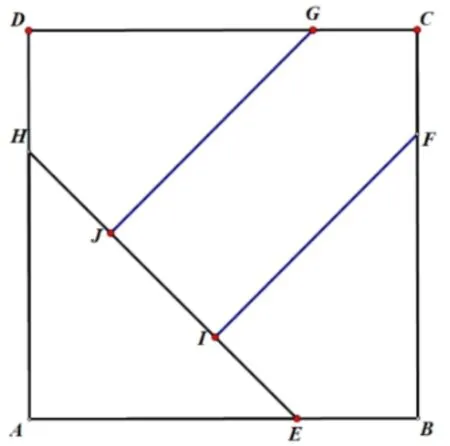
21.In squareABCD,pointsEandHlie onand,respectively,so thatAE=AH.PointsFandGlie onand,respectively,and pointsIandJlie onso thatandSee the figure below.TriangleAEH,quadrilateralBFIE,quadrilateralDHJG,and pentagonFCGJIeach has area 1.What isFI2?

译文在正方形ABCD中,点E,H分别在边和上,AE=AH,点F,G分别在边和上,点I,J在边上,使得如图所示,三角形AEH,四边形BFIE,DHJG和五边形FCGJI的面积均为1.则FI2是多少?

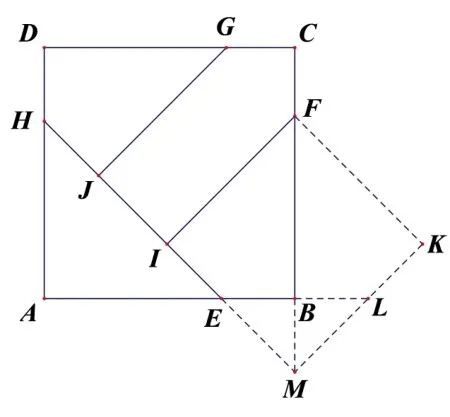
解由题意知,SABCD=4,AE=从而AB=2,BE=2-作四边形BFIE关于BF的对称图形BFKL,分别延长IE和KL且相交于点M,连接BM,则可得四边形FKMI是一个正方形,如图示.于是

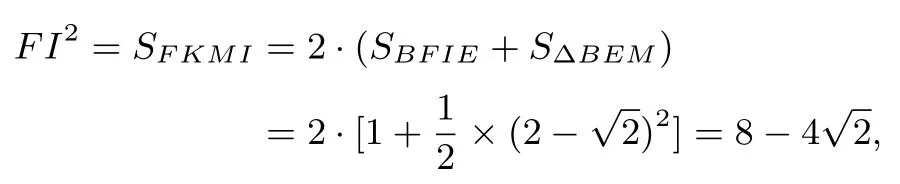
故(B)正确.

22.What is the remainder when 2202+202 is divided by 2101+251+1?

(A) 100 (B) 101 (C) 200 (D) 201 (E) 202

译文2202+202 被2101+251+1 除后的余数是多少?

解令250=x,则2202+202=4x4+202,2101+251+1=2x2+2x+1,由多项式的带余除法,可得4x4+202=(2x2+2x+1)·(2x2-2x+1)+201.故余数为201,(D)正确.

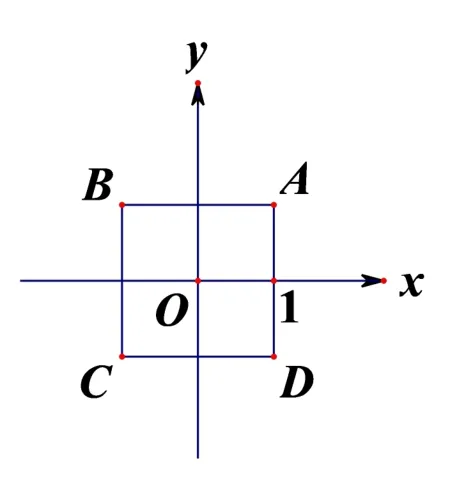
23.SquareABCDin the coordinate plane has vertices at the pointsA(1,1),B(-1,1),C(-1,-1),D(1,-1).Consider the following four transformations:

L,a rotation of 90°counterclockwise around tic origin;

R,a rotation of 90°clockwise around tic origin;

H,a reflection across thex-axis;

V,a reflection across they-axis,

Each of these transformations maps the square onto itself,but the positions of the labeled will change.For example,applyingRand thenVwould send the vertexAat(1,1)to(-1,-1)and would send the vertexBat (-1,1)to itself.How many sequences of 20 transformations chosen from{L,R,H,V}will send all of the labeled vertices back to their positions? (For example,R,R,V,His one sequence of 4 transformations that will send the vertices back to their original positions.)

(A) 237(B) 3·236(C) 238(D) 3·237(E) 239

译文坐标平面中的正方形ABCD顶点分别为A(1,1),B(-1,1),C(-1,-1),D(1,-1).考虑以下四种变换:

L,绕原点做90°的逆时针旋转;

R,绕原点做90°的顺时针旋转;

H,关于x轴的反射;

V,关于y轴的反射.

每一种变换都将这个正方形映回自身,但顶点的位置会发生变化.比如,施行R和V会将点A由(1,1) 映到(-1,-1),将点B由(-1,1)映回自身.从集合{L,R,H,V}中选择20 个变换,有多少种顺序方式可以将四个顶点均映回自身? (比如,R,R,V,H就是一种4 个变换的顺序方式,它将四个顶点均映回自身.)

解我们记正方形ABCD经过变换后得到的正方形分别在第一、二、三、四象限的顶点顺序.例如:变换L将ABCD映成DABC,LL将ABCD映成CDAB.经过一对变换之后,结果只可能为如下四种:

(1)ABCD映成ABCD:恒等变换,通过4 种方式LR,RL,HH,V V可得;

(2)ABCD映成CDAB:相当于中心对称变换,通过4种方式LL,RR,HV,V H可得;

(3)ABCD映成ADCB:相当于交换B,D两点,通过4种方式LV,RH,HL,V R可得;

(4)ABCD映成CBAD:相当于交换A,C两点,通过4种方式LH,RV,HR,V L可得.

因此,首先经过18 个任意变换之后,其结果也只可能是ABCD,CDAB,ADCB,CBAD中的一种,且是等概率的.此时,只需要再经过一对变换即可映回ABCD,且均有4 种方式.

故将ABCD映回自身的方式共有418×4=238种,(C)正确.

24.How many positive integers satisfy=(recall thatis the greatest integer not exceedingx.)

(A) 2 (B) 4 (C) 6 (D) 30 (E) 32

译文有多少个正整数满足(注意表示不超过x的最大整数.)

解设则k≥1,0≤r＜1.于是且n=70k-1000,从而原方程可化为k2-70k+1000+2kr+r2=0,即(k-20)(k-50)+2kr+r2=0.当r=0时,解得当r＞0 时,解得故共有6 组解,(C)正确.

25.LetD(n)denote the number of ways of writing the positive integernas a productn=f1·f2·····fk,wherek≥1,thefiare integers strictly greater than 1,and the order in which the factors are listed matters (that is,two representations that differ only in the order of the factors are counted as distinct).For example,the number 6 can be written as 6,2·3,3·2,soD(6)=3.What isD(96)?

(A) 112 (B) 128 (C) 144 (D) 172 (E) 184

译文设D(n)表示正整数n写成乘积n=f1·f2·····fk的方式数目,其中k≥1,且fi是严格大于1 的整数,因子的排列顺序也考虑在内(也就是说,两种仅因子顺序不同的表示被算作是不一样的).比如,6 可以表示成6,2·3,3·2,所以D(6)=3.则D(96)是多少?

解96=3×25,分情况讨论:

(1)1 个因子:就是表示成96,1 种方式;

(2)2 个因子:可以表示成3×32,6×16,12×8,24×4,48×2,每一种表示可以交换顺序,共10 种方式;

(3)3 个因子:可以表示成3×2×16,3×4×8,6×2×8,6×4×4,12×2×4,24×2×2,因子的顺序可以重新排列,共有4+2=30 种方式;

(4)4 个因子:可以表示成3×2×2×8,3×2×4×4,6×2×2×4,12×2×2×2,重新排列后共有2×3+=40种方式;

(5)5 个因子:可以表示成3×2×2×2×4,6×2×2×2×2,重新排列后共有=25 种方式;

(6)6 个因子:可以表示成3×2×2×2×2×2,重新排列后共有=6 种方式.

由加法原理,可得112 种方式,故(A)正确.