含有指数和对数的函数不等式问题的求解策略

广东省中山市中山纪念中学(528454) 李文东

同时含有指数和对数的函数的不等式问题是高考中的重点也是难点问题,此类问题常常在压轴题的位置出现,难度很大,而且直接求导后导函数往往比较复杂,只有少部分简单类型能够直接求导求解,其思考角度比较独特.本文针对此类问题给出了常见的一些求解策略.

策略一:极值点在同一位置,直接求导判断单调性

例1若不等式ex(2x3-3x2)-lnx-ax＞1 恒成立,求实数a的取值范围.

解ex(2x3-3x2)-lnx-ax＞1 恒成立,分离参数得:a＜ex(2x2-3x)-令f(x)=ex(2x2-3x)-则f′(x)=ex(2x+3)(x-1)+显然f′(1)=0,且当x＞1 时,f′(x)＞0,f(x) 递增;当0＜x＜1 时,f′(x)＜0,f(x)递减;故a＜fmin(x)=f(1)=-e-1.

点评指数部分和对数部分的极值点在同一位置,可以直接判断出函数的单调性,这属于此类问题中比较简单特殊的情形,求导后需要仔细观察导函数即可!

策略二:虚设零点,设而不求

例2已知函数f(x)=axex-1,g(x)=lnx+kx.

(1)求g(x)的单调区间;

(2)若k=1,f(x)≥g(x)恒成立,求实数a的取值范围.

解(1)略.

(2)当k=1 时,f(x)≥g(x) 恒成立,即axex-1≥lnx+x恒成立,由于x＞0,故a≥令h(x)=则h′(x)=令p(x)=lnx+x,显然p(x) 递增,又p(1)=1＞0,=-1＜0,故存在惟一的使p(x0)=0 且当x∈(0,x0)时,p(x)＜0,h′(x)＞0;当x∈(x0,+∞)时,p(x)＞0,h′(x)＜0.

故hmax(x)=h(x0)=由于p(x0)=lnx0+x0=0,即x0=e-x0,从而hmax(x)=h(x0)=所求实数a的取值范围为a≥1.

点评本题是一道精妙设计的好题,函数h(x)在x0处取得最大值,虽然x0无法直接求出,但是利用lnx0+x0=0代换后可以求出h(x0)的具体值.零点的设而不求是解决此类问题的一个重要方法,它就是针对导函数有零点且零点难以求出的情况,解题时有时还需要借助零点定理确定零点的范围才能求解.

策略三:利用不等式局部放缩

例3若不等式xe2x-lnx-ax≥1 恒成立,求实数a的取值范围.

解不等式xe2x-lnx-ax≥1 恒成立,分离参数得:a≤由 于ex≥x+1,故xe2x=e2x+lnx≥2x+lnx+1,于是≥=2,等号当且仅当2x+lnx=0时成立,显然有唯一的实数x0满足该方程.因此所求a的取值范围为a≤2.

点评本题也可用和例2 一样的虚设零点设而不求的方法求解.

例4当x＞1 时,不等式(x+1)lnx-a(x-1)＞0 恒成立,求实数a的取值范围.

解不等式(x+1)lnx-a(x-1)＞0 恒成立,分离参数得:由于故等号当且仅当x=1 时成立,因此所求a的取值范围为a≤2.

点评a＜f(x)恒成立,则a＜fmin(x).为求f(x)的最小值,我们可以适当放缩,若能得到f(x)≥g(x)≥m,并且等号同时成立,则fmin(x)=m.

例5证明:当x∈(0,1)∪(1,+∞)时,ex-＞0.

证明由于故构造函数要证原不等式,只需证:即证当x＞1 时,lnx＞成立;当0＜x＜1时,lnx＜成立.令f(x)=lnx-则故f(x)递增,又f(1)=0,可见所证成立.

点评本题也可以采用切线放缩:易求得函数和函数g(x)=在x=1 处的切线分别为和从而有一般,对于指数函数,我们常用的放缩有:ex≥x+1⇒ex-1≥x⇒ex≥ex,

策略四:根据函数的结构特征,构造同构式

例6若对任意x＞0,a(eax+1)≥恒成立,求实数a的取值范围.

解不等式a(eax+1)≥两边同乘 以x得:ax(eax+1)≥2(x2+1lnx,进一步有(eax+1)lneax≥(x2+1)lnx2.令f(x)=(x+1)lnx,则原不等式等价于:f(eax)≥f(x2).又易知f(x)在(0,+∞)上递增,故eax≥x2,取对数分离参数可得:令易知g(x)在(0,e)上递增,在(e,+∞)上递减,故a≥2·gmax(x)=

点评当函数f(x)的表达式比较复杂时,我们可以对其进行等价变换,比如换元法,同构法等,使得问题达到简化的目的!

例7当x＞0 时,(ex-1)ln(x+1)＞x2.

证明

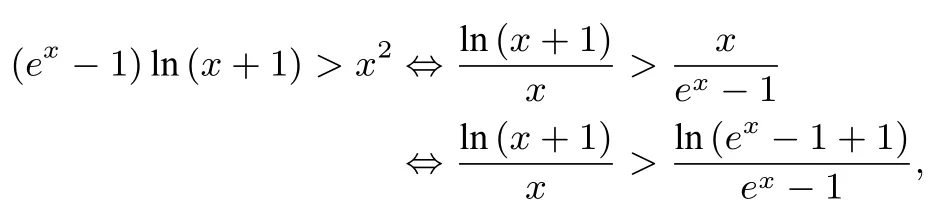
令f(x)=所证为f(ex-1)＜f(x).又当x＞0时,ex-1＞x,故只需证f(x) 在(0,+∞) 上递减.因为f′(x)=而故f′(x)＜0.

点评本题也可采用ex＞1+x+放缩来证明.

一般地,常见的同构类型有:

类型1aea≤blnb,它可以从以下三个角度同构:

(1)改写左边:ealnea≤blnb,构造函数f(x)=xlnx;

(2)改写右边:aea≤(lnb)elnb,构造函数f(x)=xex;

(3)取对数:a+lna≤lnb+ln(lnb),构造函数f(x)=x+lnx.

类型2它可以从以下三个角度同构:

(3)取对数:a-lna＜lnb-ln(lnb),构造函数f(x)=x-lnx.

类型3ea±a＞b±lnb,它可以从以下两个角度同构:

(1)改写右边:ea ±a＞elnb ±lnb,构造函数f(x)=ex±x;

(2)改写左边:ea ±lnea＞b±lnb,构造函数f(x)=x±lnx.

类型4拼凑后再同构:

(1)aeαx＞lnx⇒axeax＞xlnx,转化为类型1;

(2)a(eax+1)≥⇒ax(eax+1)≥转化为类型1.

策略五:指数对数分离,直线隔离

例8(2014 高考新课标卷) 证明:当x＞0 时,

证明令f(x)=exlnx+从而所证f(x)＞1等价于xlnx＞设函数g(x)=xlnx,则g′(x)=1+lnx.所以当x∈时,g′(x)＜0;当x∈时,g′(x)＞0.故g(x)在上单调递减,在上单调递增,从而g(x)在(0,+∞)上的最小值为

设函数h(x)=则h′(x)=e-x(1-x).所以当x∈(0,1) 时,h′(x)＞0;当x∈(1,+∞) 时h′(x)＜0.故h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,从而h(x)在(0,+∞)上的最大值为h(1)=综上,当x＞0时,g(x)＞h(x),即f(x)＞1.

点评通过变形后求转化为:f(x)＞g(x),通过常数隔离后转化为fmin(x)＞gmax(x).

例9(2013年高考全国卷)设函数f(x)=ex-ln(x+m),当m≤2 时,证明f(x)＞0.

证明函数y=ex在x=0 处的切线方程为y=x+1,从而有ex≥x+1,等号当且仅当x=0 时成立;而函数y=ln(x+m)在x=1-m处的切线方程为y=x+m-1,函数y=ln(x+m)为凸函数,从而ln(x+m)≤x+m-1,等号当且仅当x=1-m时成立;因为m≤2,故ln(x+m)≤x+m-1≤x+1≤ex,又等号不同时成立,从而ln(x+m)＜ex.

点评这里我们采用切线隔离的方式,本题也可以采用虚设零点设而不求的方法求解.

策略六:利用端点效应

例10(2016年高考四川卷)设函数f(x)=ax2-a-lnx,其中a ∈R.

(1)讨论f(x)的单调性;

(2)确定a的所有可能取值,使得在区间(1,+∞)内恒成立(e=2.718···为自然对数的底数)

解(1)略.

g(x)=注意到g(1)=0,故可得

另一方面,当a≥时,

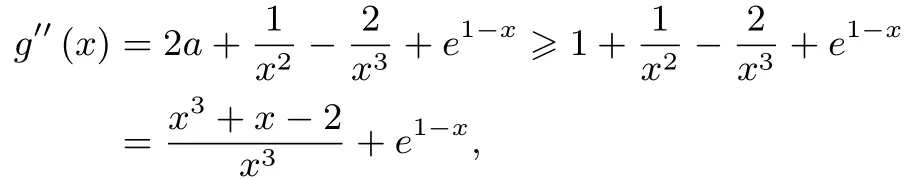
所以x∈(1,+∞),故x3+x-2＞0,e1-x＞0,于是g′′(x)＞0.所以当a≥时,g′(x) 在x∈(1,+∞) 单调递增.所以g′(x)＞g′(1)=2a-1≥0,故g(x) 在x∈(1,+∞)单调递增.所以g(x)＞g(1)=0,即g(x)在(1,+∞)上恒大于0.综上,

以上是解决含有指数和对数的函数不等式问题的求解策略,具体求解时,我们需要仔细观察函数的特征,从以上角度去多方面尝试,采取合理的策略.