蒙日圆问题的拓展变式研究*

广东省中山市中山纪念中学(528454) 鞠火旺

受文[4]研究思路的启发,我们将蒙日圆问题的约束条件“两条垂直的切线”改为“两条切线的斜率之和差积商为定值”,并称切线交点的轨迹为相应圆锥曲线的伴随曲线,通过在Geogebra 实验环境中探究,我们发现了伴随曲线的性质并给出了证明.

结论1过椭圆C:外一点P引椭圆的两条切线PA和PB,若kPB·kPA=δ,其中δ为常数且δ≠0,则两切线的交点P的轨迹方程为δx2-y2=δa2-b2,且OA、OB的斜率之积为定值,即

证明设点P(x0,y0),切线PA、PB的斜率分别为k1和k2,切线方程为y-y0=k(x-x0).联立得

(a2k2+b2)x2-2a2(kx0-y0)kx+a2((kx0-y0)2-b2)=0,

由于直线与椭圆相切,于是

Δ=(-2a2(kx0-y0)k)2-4(a2k2+b2)a2((kx0-y0)2-b2)=0,

化简整理得

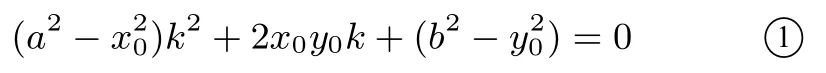
因为k1、k2为①式的两根,由韦达定理得k1k2=从而两切线交点P的轨迹方程为δx2-y2=δa2-b2,该伴随曲线的类型取决于δ的取值范围.

当δ=-1 即两条切线互相垂直时,伴随曲线为x2+y2=a2+b2,这就是蒙日圆.

当δ＜0 且δ≠-1 时,伴随曲线1 是椭圆,见图1.

当δ=时,伴随曲线为两条直线y=在椭圆C外的部分,见图2.

当δ＞0 且δ≠时,伴随曲线为双曲线,其中,当时,伴随曲线是双曲线在椭圆C外的部分;当时,伴随曲线是双曲线在椭圆C外的部分,分别见图3和图4.

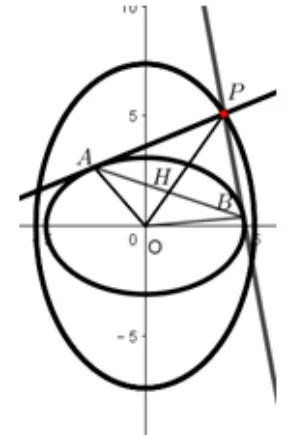
图1.δ＜0 且δ≠－1 的情形

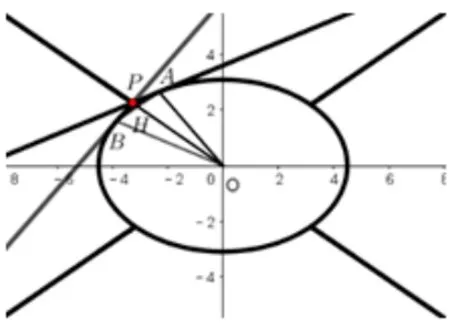
图2.δ=的情形

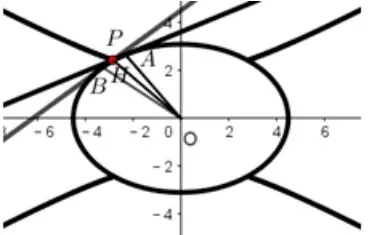
图3.δ∈(0,)的情形

图4.δ∈(,+∞)时的情形

下证OA、OB的斜率的乘积为定值,为此不妨设A(x1,y1),B(x2,y2),AB的中点为H,切点弦方程为即

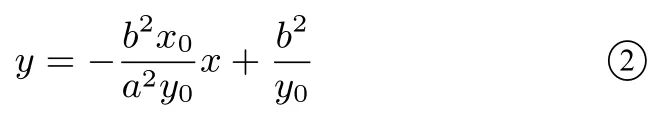
又A(x1,y1)∈l,于是kPA=-又kOA=因此

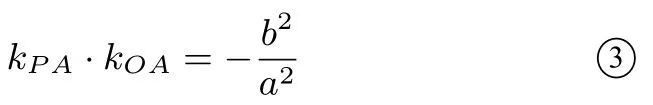
同理kPB·kOB=于是kPA·kOA·kPB·kOB=而kPA·kPB=δ,故kOA·kOB=

结论2过椭圆C:=1 外一点P引椭圆的两条切线PA和PB,若=δ,其中δ为常数且δ≠±1,则两切线的交点P的轨迹方程为且OB、OA的斜率之比为定值,即=δ.

证明因为k1、k2为①式的两根,于是由韦达定理得

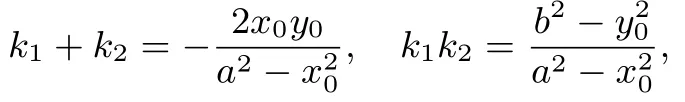
于是两切线的交点P的轨迹方程为

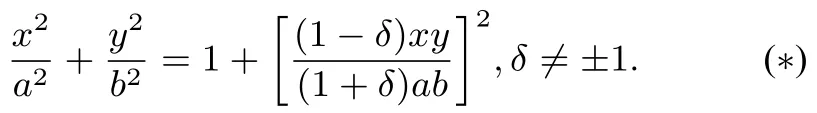
注意到方程(*)是x、y的幂都是偶数,因此伴随曲线关于x轴,y轴是轴对称的.又由问题的实际意义可知,当δ=1 时轨迹不存在,当δ=-1 即kPB=-kPA时,轨迹是椭圆外与坐标轴重合的四条射线,见图5.

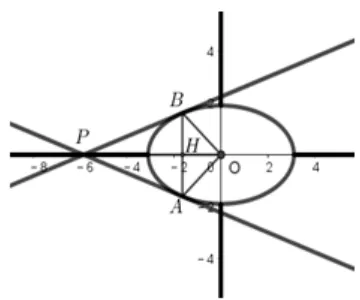
图5.δ=－1 的情形

再注意到伴随曲线的方程中x、y是对称的,于是y=±b是其水平渐近线.借助Geogebra 软件我们可以清晰地看到该伴随曲线的图像,见图6～图9.

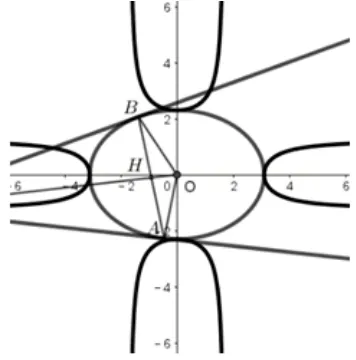
图6.δ＜0 且δ≠－1 的情形

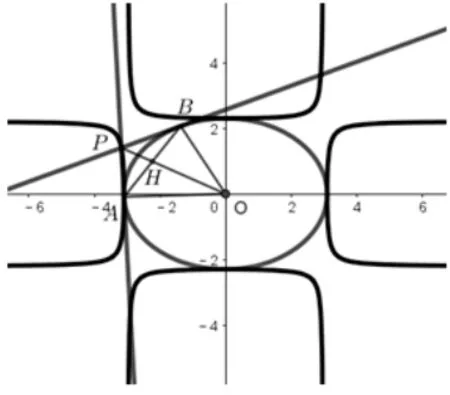
图7.δ→－∞时的情形

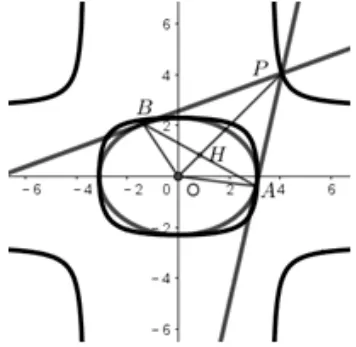
图8.δ＞0 的情形

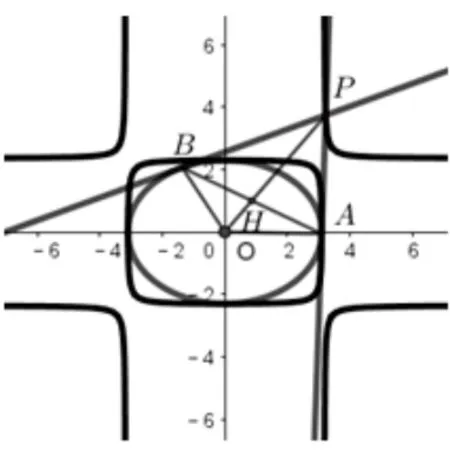
图9.δ→+∞的情形

结论3过椭圆外一点P引椭圆的两条切线PA和PB,若kPB+kPA=δ,其中δ为常数且δ≠0,则两切线的交点P的轨迹方程为δx2-2xy=δa2,且OA、OB的斜率的倒数之和为定值,即

证明由①式结合韦达定理知从而两切线交点P的轨迹方程为δx2-2xy=δa2,注意到该方程可以化为这是常见的“双刀型”函数.

当δ＜0 时,伴随曲线在(-∞,0)及(0,+∞)都是单调递减的;当δ＞0 时,伴随曲线在(-∞,0)及(0,+∞)都是单调递增的,即两切线交点所形成的椭圆的伴随曲线是“双刀型”函数在椭圆C外的那一部分,其图像见图10和图11.

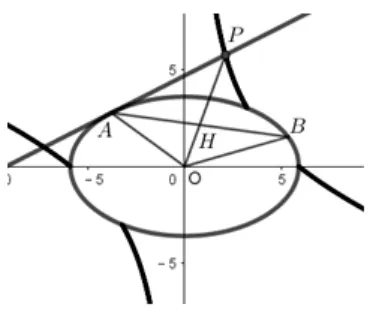
图10.δ＜0 的情形

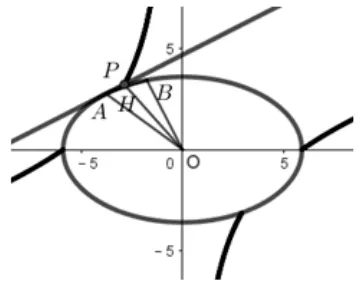
图11.δ＞0 的情形

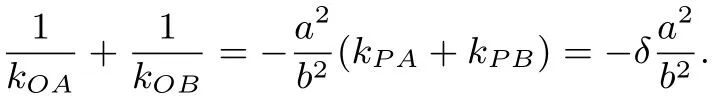
结论4过椭圆外一点P引椭圆的两条切线PA和PB,若kPB-kPA=δ,则两切线的交点P的轨迹方程为

且OA、OB的斜率的倒数之差为定值,即

证明将k2-k1=δ代入②式得

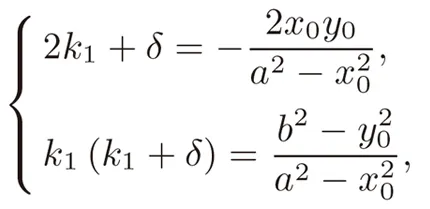
消去k1并化简整理得

于是两切线的交点P的轨迹方程为

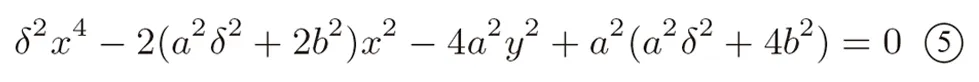
将y用x表示出来(为方便起见,我们只研究y＞0 的情形),得到函数

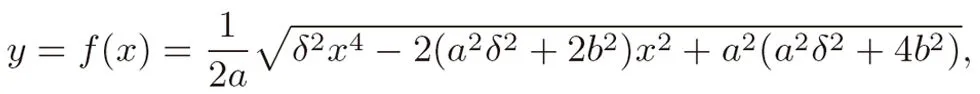
该函数的定义域为

由

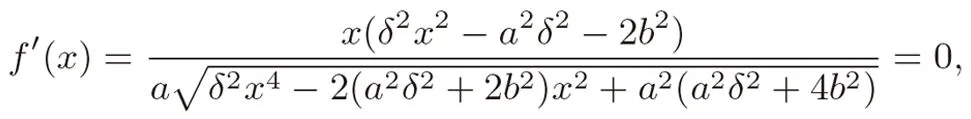
得x=或x=0 或x=结合函数的定义域及单调性可得函数y=f(x)的图像如图12所示,因此由⑤式确定的伴随曲线的图像如图13所示,这与直接作图产生的轨迹曲线是相吻合的;此外,定值的证明与结论3 中的方法类似,这里略去.

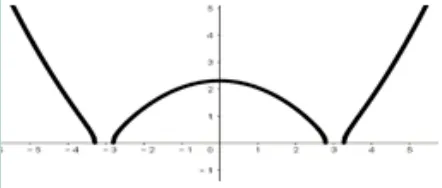
图12.函数y=f(x)的图像

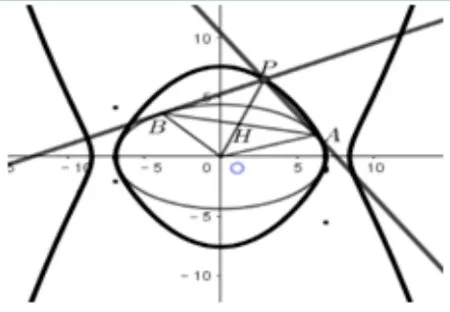
图13.伴随曲线的图像

至此,我们对椭圆的伴随曲线作了较详细的研究,在双曲线及抛物线中也有类似的性质,限于篇幅,我们就不再一一赘述.