汽车运行工况的构建方法

汪雯琦，高广阔，王子鉴，梁易鑫

(上海理工大学 管理学院，上海 200093)

0 引言

目前，我国汽车运行工况的相关标准主要是在上个世纪引进的德国和欧洲标准。这些标准与我国汽车运行工况的差异很大。近年来，随着汽车保有量的快速增长和城市化率的不断增加，我国道路交通状况变化很大,且不同地区汽车运行工况差异很大，目前缺乏统一适用的标准。当前，制订出适合我国各地国情的油耗标准和排放规范是当务之急。

运动学片段是指汽车从怠速状态开始至相邻的下一个怠速状态开始之间的车速变化状况的连续过程，如图1所示。本研究设计了一种合理的方法，将预处理后的数据划分为多个运动学片段，并给出通过数据文件处理计算得到的运动学片段的最终数量[1]。

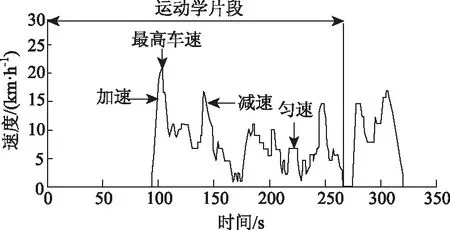
图1 运动学片段的定义Fig.1 Definition of kinematic segment

为了在国际市场上占据新一代能源汽车性能的领先地位，欧洲、日本、美国加快了汽车运行工况的研发[2-7]。近年来，国内学者也开始对车辆的运行状况进行深入研究[8-9]。多数学者采用结合主成分分析(PCA)和K-means聚类法来进行汽车运行工况的拟合，但传统K-means聚类算法的初始聚类中心会导致聚类结果下降，陷入局部最大值。胡宸等[10]、胡志远等[11]使用PCA、K-means聚类分别构建了哈尔滨和上海的车辆运行工况，但均未在初始聚类中心的基础上寻优。石琴等[12]改进了初始聚类中心，并使用神经网络算法构建了汽车运行工况，但神经网络需要设置初始权值，导致聚类质量下降。

本研究将在公共交通系统、城市发展及汽车排放标准方面起到推动作用，其意义主要体现在：

(1)有助于公共交通系统的建设与发展，减少汽车怠速时间和缓解城市拥堵，从而提高出行效率。

(2)能规范城市汽车市场准入标准，解决汽车采购中的乱象，有助于有关部门掌握车辆的实际使用情况，提升政府决策能力。(3)车辆运行工况的变化对汽车燃料消耗和污染物排放有重要影响，在节能减排和环境保护以及在国际市场上抢占新能源汽车性能的领先地位有重要作用。

1 模型

1.1 原始数据

用行车记录仪采集记录上海市某辆轻型汽车在实际普通道路上行驶的数据，采集3次包括3个不同时间段的信息，采样频率为1 Hz。先判断各个指标所代表的含义。“速度”提供了车辆的速度信息，由于采样时间的间隔为1 s，因此也可计算出车辆行驶加速度。“三轴加速度”提供了车辆3个轴向的加速度信息，对后续速度与加速度的计算与分析意义不大。“经纬度信息”提供了计算行驶距离的可能性，可根据具体公式计算汽车行驶距离。“发动机转速”和“节气门开度”[13]有助于判断汽车是否处于熄火状态。其他变量也会为研究汽车运行状况提供帮助。车辆主要结构、配置和性能参数情况见表1。

表1 试验车辆情况Tab.1 Conditions of experimental vehicles

1.2 数据预处理

1.2.1缺失数据填充

由于高层建筑遮挡或经过隧道等，行车记录仪所记录的信息会出现GPS信号过弱或丢失，造成数据记录不连续。首先判断数据丢失时汽车可能的行驶状态，以便采用不同方法对缺失数据进行填充。数据丢失时汽车可能处于以下3类行驶状态。

第1类：缺失数据时间前后的行驶速度均大于10 km/h，认为在信号丢失的这段时间内汽车处于正常行驶状态，可能由于高层建筑覆盖或过隧道等原因造成了信号丢失。根据信号丢失前后的GPS速度，利用线性插值法对丢失的速度进行填充。

第2类：缺失数据时间前一个状态GPS速度为0且油门踏板开度也为0，则认为发动机未处于运行状态，故车辆处于熄火状态，GPS可能也处于待机状态，未检测到数据信息，视为汽车怠速进行处理，将速度填充为0。对于间隔时长超过180 s的数据，按照怠速长度180 s进行处理。

第3类：缺失数据时间前一个状态GPS车速为0或小于10 km/h，而加速踏板位移不为0，可能由于进隧道长时间堵车等原因造成，认为这一阶段处于怠速，按照车速为0进行数据填充。

对于时间不连续问题的处理，将后一个数据的秒数减去前一个数据的秒数，若差值等于1，则继续进行；若差值不等于1，需要将其标记为0并返回该值所在的位置，进而提取缺失时间数据前后的速度和加速踏板位移值，以判断车辆在信号丢失时间段的可能行驶状态。对于不同的行驶状态，采用上述方法进行相应处理。

利用Matlab进行计算，发现724处时间不连续的情况，符合上述第1类情况的时间间隔有429处，符合第2类的有189处，符合第3类的有106处，分别进行相应的处理与填充。

1.2.2平滑速度异常状态数据

行车记录仪记录的速度单位为km/h，加速度的单位为m/s2，所以先对速度进行单位转化，使其单位变为m/s，计算公式为：

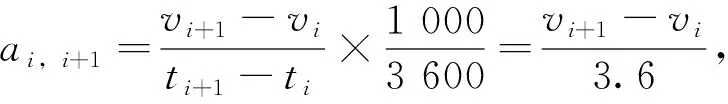
i=1, 2，…，k-1,

(1)

式中，ai,i+1为第is到第(i+1)s的加速度；vi+1，vi分别为第is和第(i+1)s的速度；ti+1，ti分别为第is和第(i+1)s的时刻；k为运动学片段的总时间，也是总速度的个数。

根据式(1)算出各个时间点上的加速度值。通常认为，一般情况下，普通轿车0～100 km/h的加速时间大于7 s，紧急制动最大减速度为7.5～8 m/s2。所以可认为当加速度大于3.97 m/s2或减速度小于-8 m/s2时为异常值。采用移动平均滤波器Smooth函数进行平滑处理以消除这些异常值，默认窗宽为5。

1.2.3长期停车数据处理

对长期停车(如停车不熄火等候人、停车熄火但采集设备仍在工作等)所采集的异常数据，首先明确长时间停车的类型，分为是/否熄火两种情况进行考虑。如果发动机转速为0，表示发动机已处于熄火状态，将该数据做删除处理；如果发动机转速不为0，但车速为0，按怠速处理。

1.2.4怠速情况分析

将长时间堵车、断续低速行驶状况(车速小于10 km/h)按照怠速工况处理。首先找出车辆行驶速度长时间小于10 km/h的连续时段，选择车速小于10 km/h的时间点进行划分。根据其连续性的判断与选择，合并连续的时间点，划分为若干个连续片段。如果某片段的持续时间长度大于180 s，则将这段时间视为怠速工况状态；如果持续长度未达到180 s，为了保证数据的准确性，则不作处理而保留原始速度信息。

1.2.5怠速数据处理

找到怠速时长超过180 s的片段，利用滑动窗口法进行解决。首先定义一个长度为180 s的窗口，并用这一窗口按照从上到下的顺序去截取速度为0的数据。当截取的这段数据中车速均为0时，需删除1个数据再继续截取，直至遍及所有数据。为了提高滑动速度，若截取到的1段数据的最后一个车速值不为0，就直接跳过这一片段，继续进行滑动。最后保证数据集中没有出现超过180 s的怠速工况。

数据的预处理均利用Matlab软件编程解决。在补齐缺失数据、处理或剔除异常值数据后，行车记录仪在3个不同时间段采集的数据最终记录数分别为205 990，173 368，180 786。预处理前后的数据对比如图2所示。

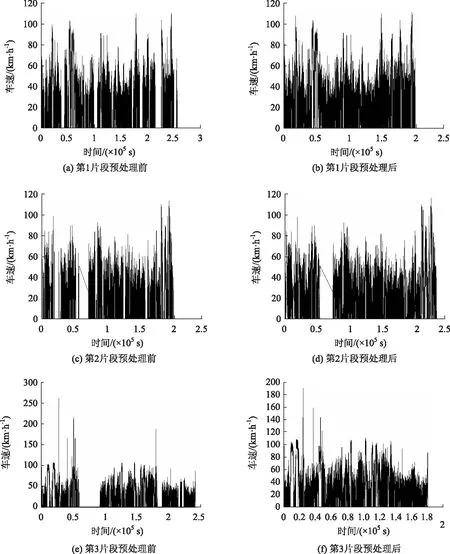
图2 三个片段运动学数据预处理前后对比Fig.2 Comparison of kinematic data of 3 segments before and after preprocessing

2 运动学片段的提取

2.1 运动学片段相关理论

在构建道路运动工况的过程中存在着多种方法，其中应用最为广泛的是将全部试验数据按照某种既定原则划分为若干个片段，并对所有小片段进行研究。选择适当的方法构建运行工况，而其中这些片段即为运动学片段(从怠速状态开始至相邻的下一个怠速状态开始之间车速变化状况的连续过程)。用此方法构建的运行工况更符合实际。

将上述运动学片段中的几种运动学状态进行划分如下。

(1)怠速工况：发动机工作，且车辆速度V为0的状态。

(2)匀速工况：车辆加速度a小于0.10 m/s2并大于-0.10 m/s2，且V不为0的状态。

(3)加速工况：车辆加速度a大于0.10 m/s2，且V不为0的状态。

(4)减速工况：车辆减速度a小于-0.10 m/s2，且V不为0的状态。

2.2 运动学片段的划分

为构建运行工况，需要对运动片段进行划分。划分标准是：从怠速状态开始至相邻的下一个怠速状态开始之间车速变化状况的连续过程。由于汽车行驶状况数据的试验数据量较大，且城市道路行驶过程中启停较为频繁，需要进行行程划分的数据数量较大，必须利用软件进行处理，选用Matlab软件辅助处理，分别对3个行驶数据文件的数据进行切分，形成若干运动学片段，分别划分成1 716，2 184，1 681个运动学片段。

2.3 运动学片段的特征提取与计算

表2 特征参数Tab.2 Characteristic parameters

由上述选取的特征参数中，发现加速度值较多为5个，因其不能直接通过观测得到，故需要根据GPS速度，使用相关公式进行计算。

13个特征值的计算公式如下。

加速时间百分比：

Pa=Ta÷T，

(2)

式中，Ta为运动学片段中加速度大于0.1 m/s2的时间数；T为运动学片段的总时间数。

减速时间百分比：

Pd=Td÷T，

(3)

式中，Td为运动学片段中加速度小于-0.1 m/s2的时间数。

怠速时间百分比：

P0=T0÷T，

(4)

式中T0为运动学片段中的怠速的时间数。

匀速时间百分比：

Pc=(T-Ta-Td-T0)/T。

(5)

最大速度：

vmax=max{vi,i=1, 2，…,k}。

(6)

平均速度：

(7)

式中,S为每个运动学片段所代表的汽车行驶距离。由于该试验的采样频数设置为1 Hz，即每两个点的时间间隔为1 s，所以S为该片段的速度之和，计算式为：

(8)

平均行驶速度：

Vm=S/T。

(9)

速度标准差：

(10)

式中,Vi为汽车行驶数据中按时间顺序的第i个速度;k为行驶数据的总条数。

加速度相关特征值：

(11)

通过编程对上述特征参数进行了计算，并为后续运动学片段的筛选及汽车运行工况的构建提供了重要信息。分别对3个文件中的数据进行了特征值的提取与计算，每份汽车行驶数据文件中分别选取了1张运动学片段进行前后对比。

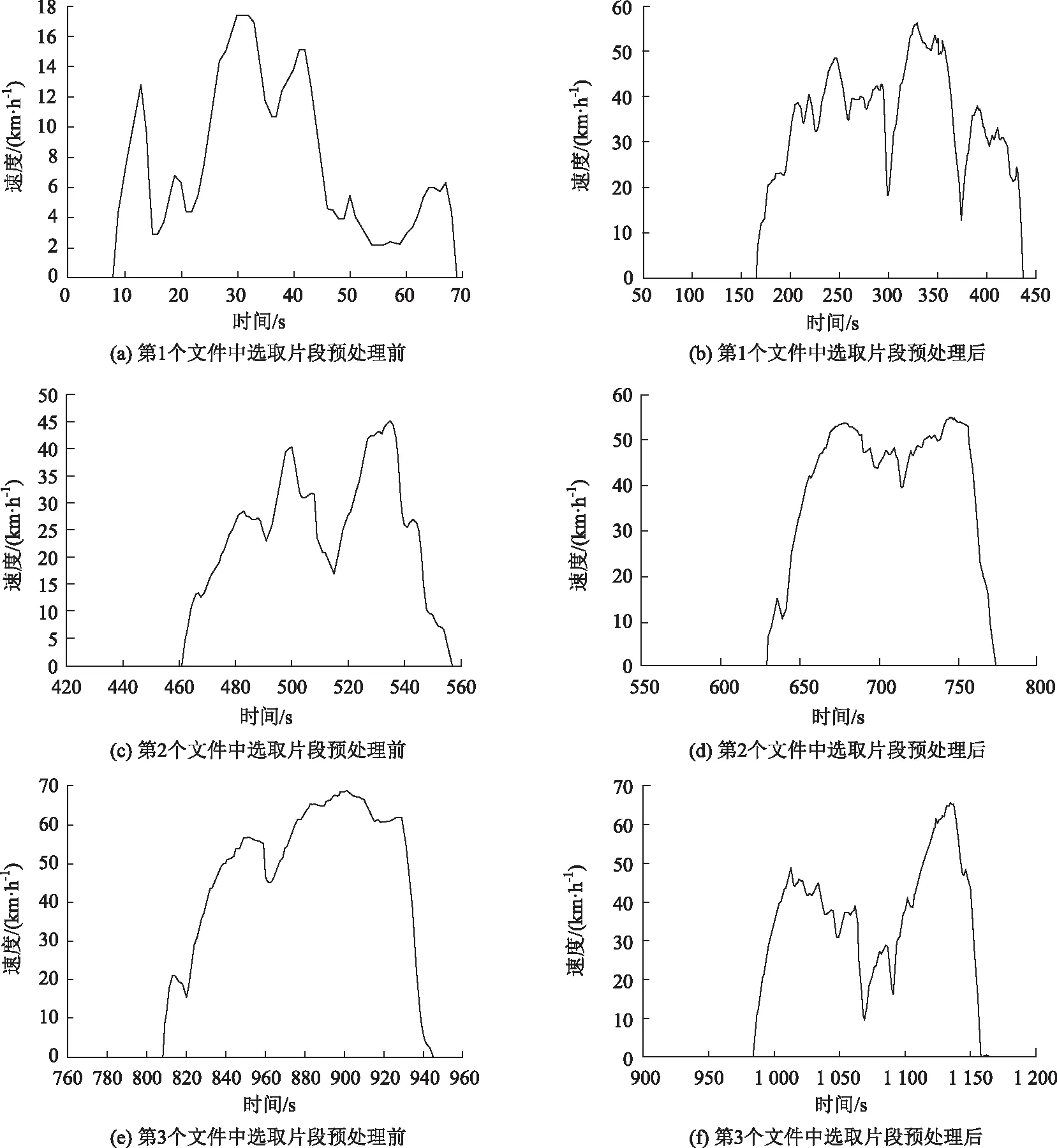
图3 三个行驶数据文件中预处理前后的汽车行驶工况对比Fig.3 Comparison of vehicle driving conditions in 3 driving data files before and after preprocessing

由图3可明确地识别该车在特定时间段的行驶状态。接下来对上述所有分割出来的运动学片段进行有效筛选，最终选取最具代表性且符合真实道路行驶的片段以构建较为准确的汽车运行工况。

3 汽车运行工况的构建

3.1 构建流程

因特征参数较多，选用主成分分析模型对特征参数进行降维处理。将13个特征参数变量转化为数量较少的几个主成分，接着以这几个主成分作为变量，运用K-means聚类模型对运动学片段进行分类，主要构建流程如图4所示。

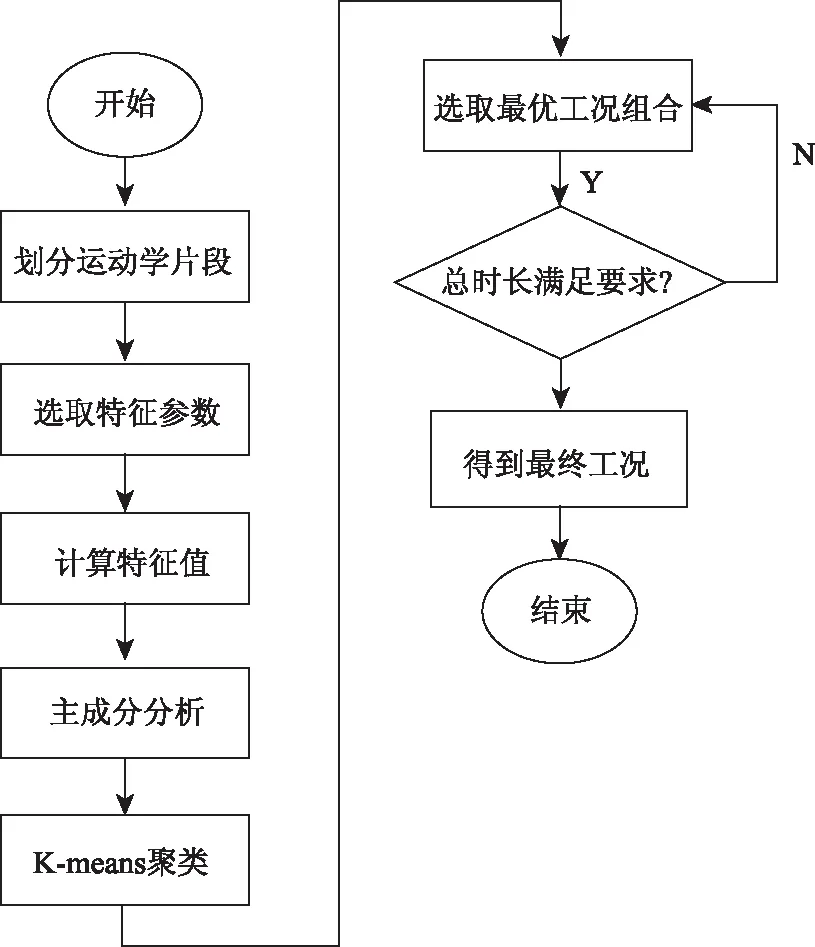
图4 汽车运行工况构建流程Fig.4 Flowchart of constructing vehicle operation condition

3.2 基于主成分分析的数据降维

按照主成分分析步骤[14]，对标准化后的特征值进行分析。计算13个特征参数的方差贡献率和累积贡献率，得到结果列在表3中。

选取累积贡献率达到80%作为基准，达到的为第4项的84.09%，且前4项主成分的特征值均大于1，基本涵盖全部信息，所以提取前4项主成分表征原始特征参数。计算因子载荷矩阵，如表4所示。

主成分1描述了平均速度、最大速度、平均行驶速度、速度标准差、最大加速度、怠速时间百分比和等速时间百分比。主成分2描述了平均减速度、平均加速度和加速度标准差。主成分3描述了最大减速度和减速时间百分比。主成分4描述了加速时间百分比。所以主成分1～4就是降维后的主成分。

根据：

(12)

式中，Mi为主成分得分序列；bij为对应的成分系数；Ym为标准化后的特征值。

从而得到第1～第4主成分的得分。经计算后式(12)变为：

(13)

主成分载荷(无量纲)见表5。

所以可得4个主成分为:

M1=0.37Y1+0.36Y2+0.35Y3+0.34Y4+0.31Y5+

0.30Y6+0.29Y7+0.01Y8-0.02Y9-0.06Y10-

0.04Y11-0.03Y12+0.1Y13，

(14)

M2=-0.02Y1-0.13Y2-0.07Y3+0.26Y4+0.31Y5+

0.30Y6+0.34Y7+0.51Y8+0.45Y9-0.44Y10-

0.08Y11-0.16Y12-0.03Y13，

(15)

M3=-0.09Y1+0.15Y2-0.07Y3-0.09Y4-0.14Y5-

0.10Y6-0.22Y7+0.01Y8-0.32Y9+0.17Y10+

0.80Y11+0.78Y12+0.02Y13，

(16)

M4=0.15Y1+0.10Y2+0.05Y3+0.18Y4+0.00Y5+

0.33Y6+0.15Y7-0.14Y8+0.03Y9-0.57Y10+

0.09Y11-0.13Y12+0.94Y13。

(17)

由上列4个表达式，通过计算变量Y1到Y13得到M1,M2,M3,M4的值。

然后进入SPSS的标准化处理，其中Y1为怠速

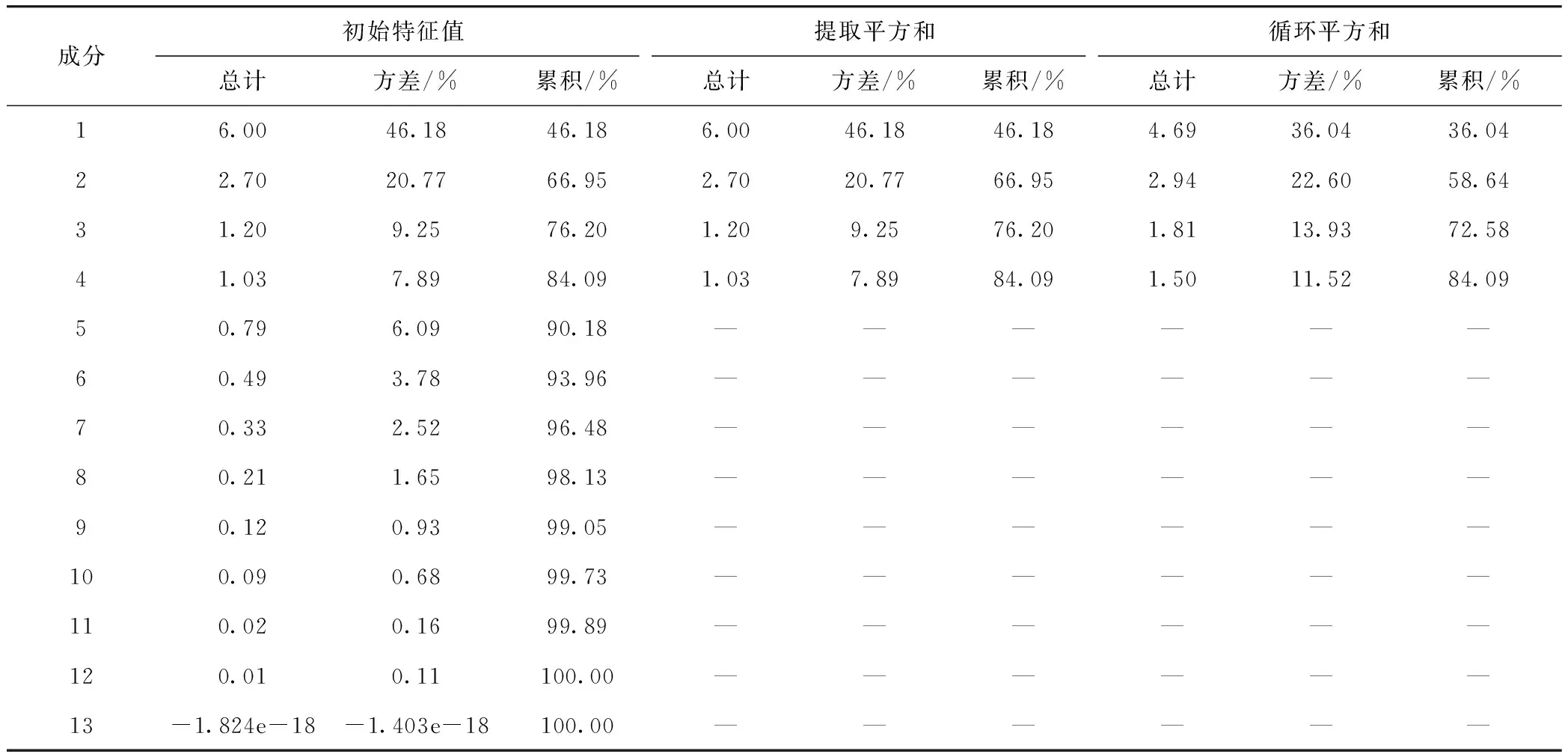
表3 运动学片段的主成分贡献率矩阵Tab.3 Principal component contribution matrix of kinematic segments

时间百分比，Y2为加速时间百分比，Y3为减速时间百分比，以此类推计算出主成分M1,M2,M3,M4的结果。

3.3 K-means聚类模型

降维处理后，运用SPSS软件以及Jupyter Notebook工具进行降维得到4个主成分分别进行分类处理。具体通过聚类分析，即经降维处理，对运动学片段数据按各自特性和一定的规则分成3类，找到了运动学片段样本数据中的相似和区别，大量减少了研究的数量，在车辆研究领域有重要意义。

3.3.1分类数量的确定

(1)初步设定

据文献[15-16]，汽车运动状态通常被分为3种：走走停停、低速行驶、高速行驶。因此，在SPSS运行时将分类数初步设定为3。

(2)轮廓系数法

在具体决定分类法个数时，采用了轮廓系数进行聚类评估。其计算公式为：

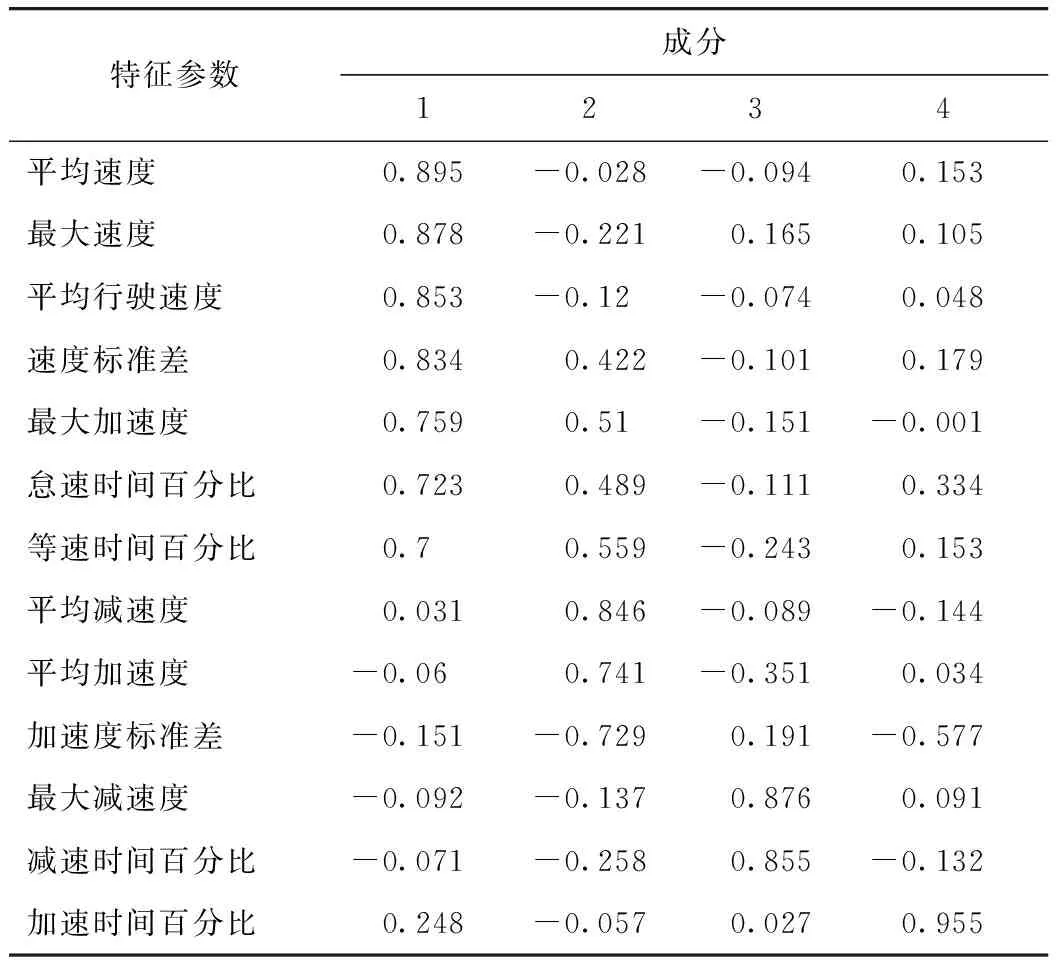
表4 运动学片段的因子载荷矩阵Tab.4 Factor load matrix of kinematic segment

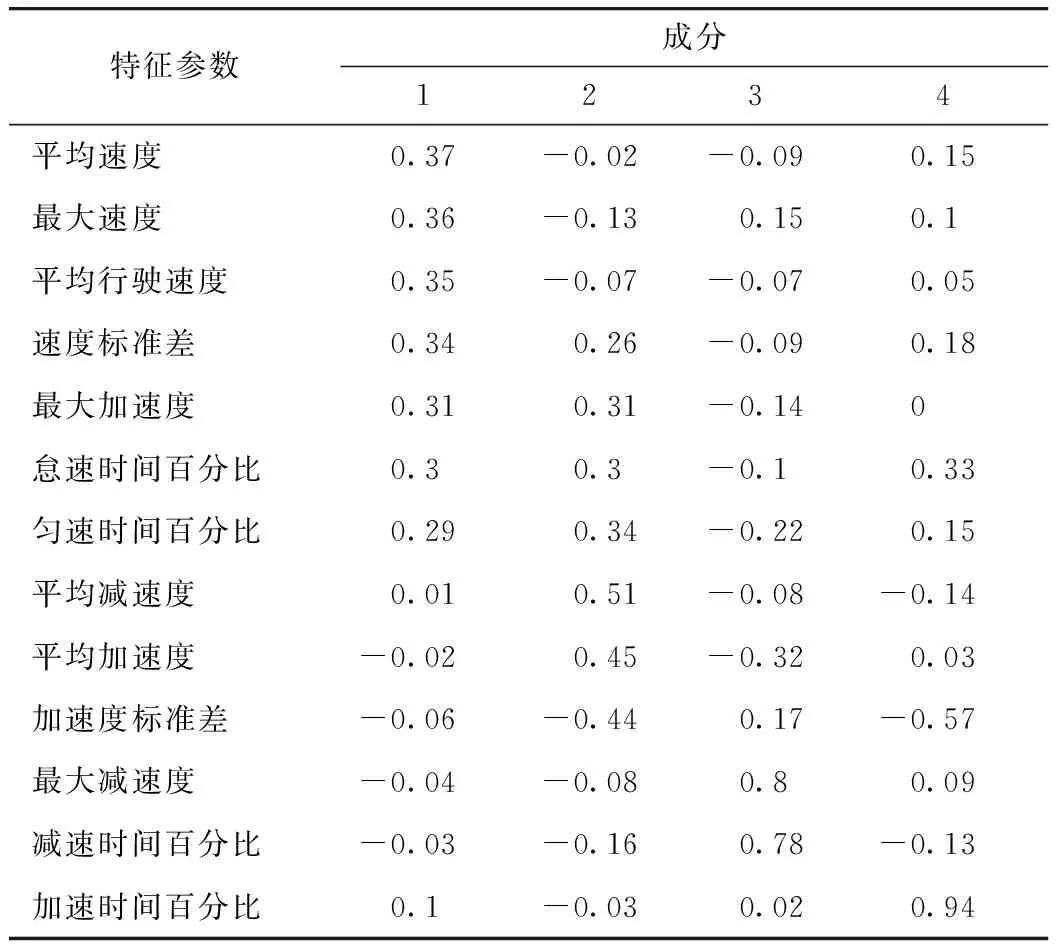
表5 主成分载荷Tab.5 Principal component loads

(18)

式中，a(i)为点i到所有它所属的簇中其他点距离的平均值;b(i)为点i到与它相邻最近的一簇内所有点平均距离的最小值。

通过Jupyter Notebook编程，得出了图5所示的初始化群集数折线图。

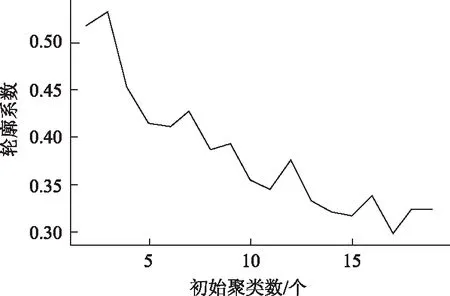
图5 初始化群集数折线图Fig.5 Line chart of initialization cluster number

由图5可知，当分类数为3时，s(i)更接近1，此时的聚类合理。这再次验证了分类为3是正确合理的。

3.3.2直观验证

根据Jupyter Notebook动态编程进行2类、3类分类尝试。经比较，分为3类合理。

3.3.3运动学片段的聚类分析

结合以上3种方法，最终确定分类数为3时最为合适。经过100次迭代，主成分被成功地分成3类，聚类中心[17]见表6。

表6 聚类中心Tab.6 Cluster centers

运动学片段聚类结果见图6。由于数据众多，为方便观测，作随机失活处理。第1类三角形图标含有3 112个运动学片段数，占总时间比例的55.76%。第2类正方形图标含有2 282个运动学片段数，占总时间比例的40.89%。第3类圆形图标含有187个运动学片段数，占总时间比例的3.35%。如图6所示，从左至右图标设置不同，分别为正方形图标、三角形图标、圆形图标。

图6 该辆车所有数据运动学片段的聚类Fig.6 Clustering of all data kinematic segments of vehicle

根据Jupyter Notebook编程将3类数据进行分析。

分析发现，第3类圆形图标：走走停停；第2类正方形图标：高速行驶；第1类三角形图标：低速行驶。这与现实情况基本吻合，再次验证了选择3种分类情况是正确的。综上所述，对于此辆汽车的运行工况数据进行分析，得出了车辆运行被分为3类，且相互之间具有明显的差异。

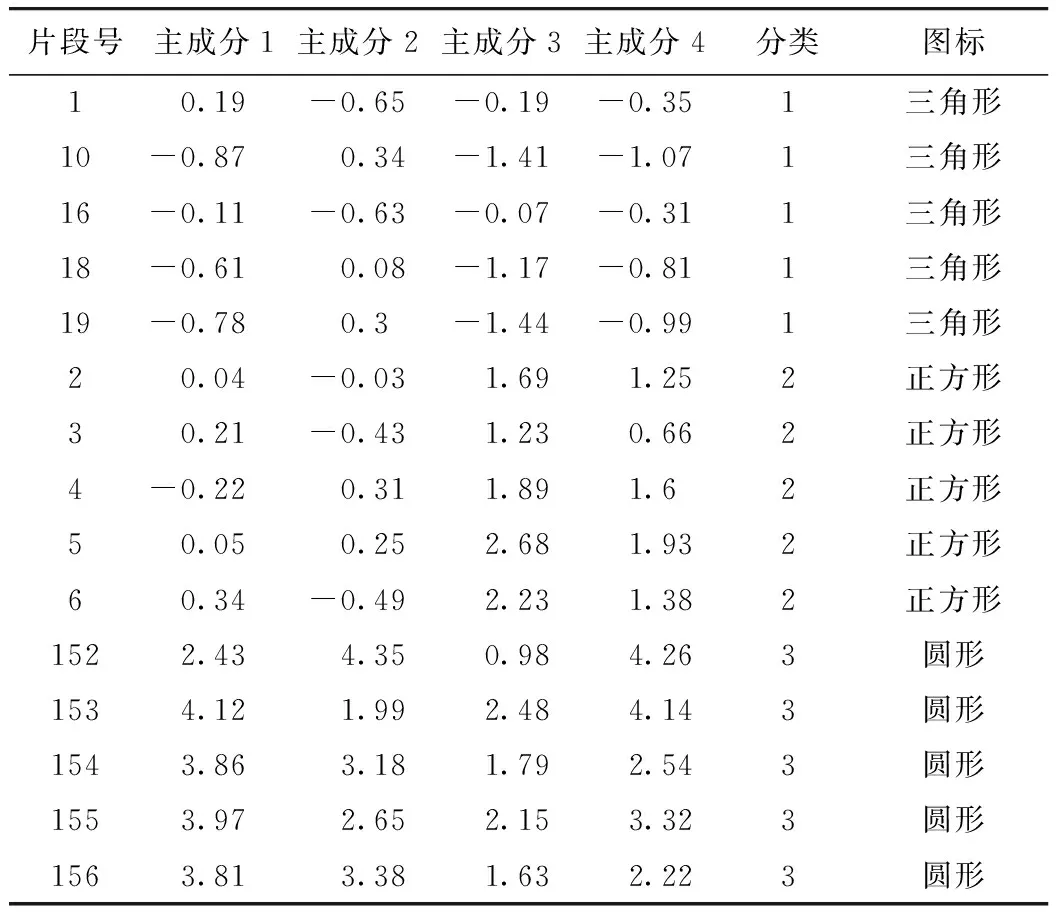
表7 部分片段分类结果Tab.7 Partial fragment classification result

3.4 构建汽车运行工况

与数据预处理后的原始数据进行匹配，得到分类后的数据特征值，然后对第1类～第3类的数据进行总体描述，得到分类后的总体数据的特征值，见表8。

接着，运用Matlab软件编程计算出与总体特征矩阵的相关系数，汇总后得出表9。

表9表示随机选出的每类与总数特征值相关性较高的计算结果，没有按照降序排列，且在生成的结果中所有的相关性系数均大于0.5，这说明聚类分析较为正确，再次验证了分为3类是合理正确的。

3.5 绘制汽车运行工况

由于第1类～第3类运动学片段的占比分别为55.76%，40.89%，3.35%。故选取了15个运动学片段，其中第1类情况中选取了6个运动学片段，第2类情况中选取了4个运动学片段，第3类情况中选取了5个运动学片段[18]。之所以选择较多片段，是因为这些运动学片段时间较短。选取的15个汽车运动学片段的情况见表10。

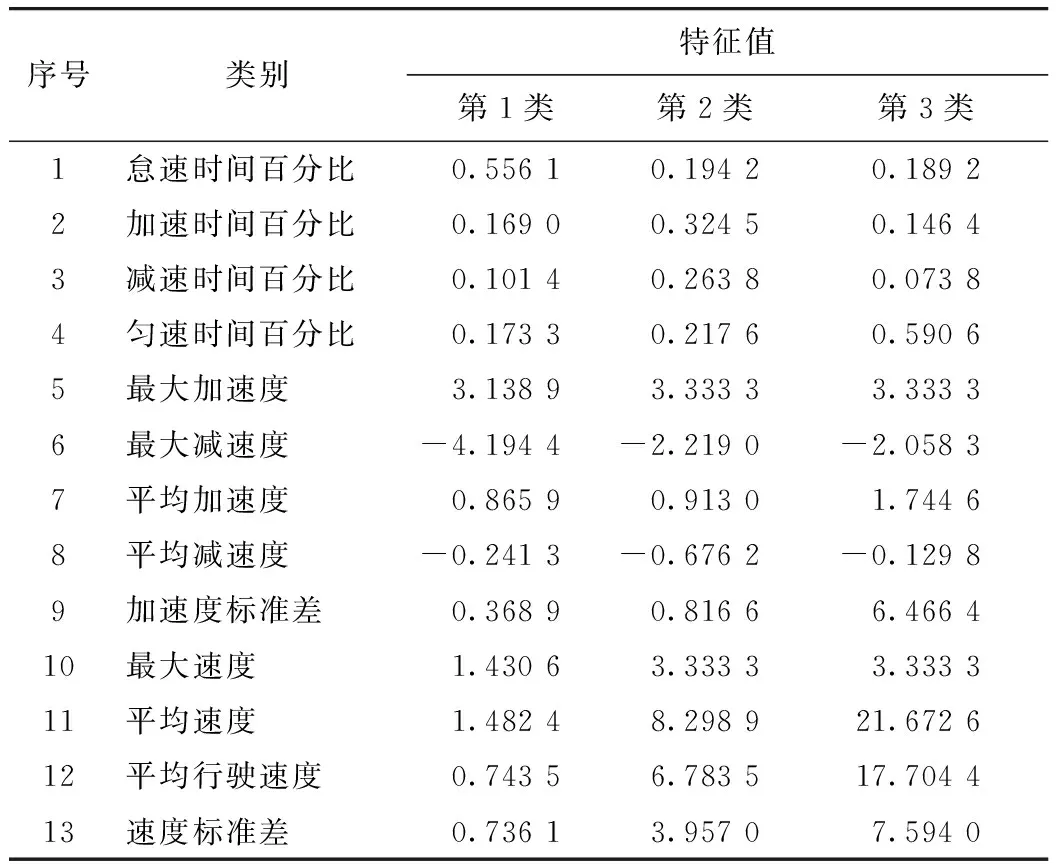
表8 总体分类后的数据特征值Tab.8 Characteristic values of data after overall classification

表9 与总体特征值相关性较高的片段Tab.9 Fragments with high correlation with the overall eigenvalues

表10 选取的运动学片段的相关性系数Tab.10 correlation coefficient of selected kinematic segments

选取的片段与总数特征值矩阵的相关性系数均为0.9以上，可以代表总体特征，相关性很强，以此绘制汽车运行工况可以起到很好的说明效果。

使用SPSS软件进行散点图的绘制，由于时间的间隔为1 s，将各个散点用直线连接起来就是车辆运行工况。图13很好地反映了汽车走走停停、加速、减速、匀速、怠速的过程，可以有效地反映车辆运行工况。

通过计算误差率，形成拟合误差分析表(表11)，拟合运行工况的绝大多数特征参数都与原始数据的参数十分接近，在10%以内，只有个别参数的误差大于10%，但都小于20%。总体说明，构建出的汽车运行工况与实际工况很相近。

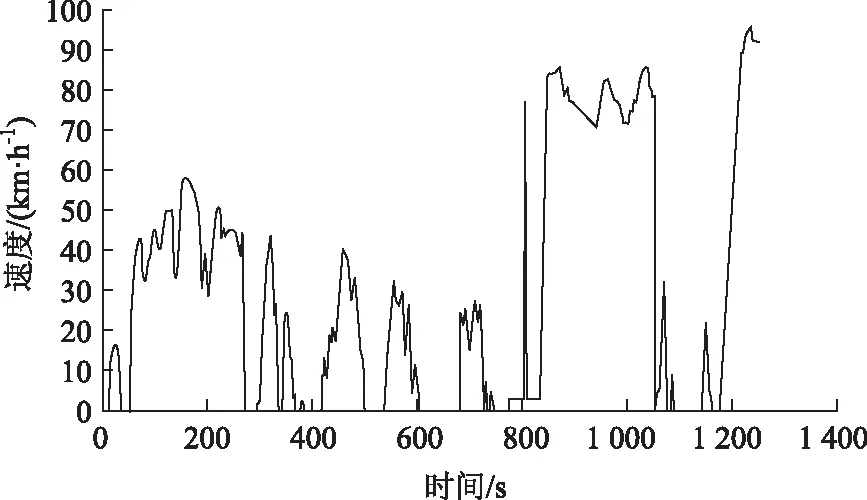
图7 车辆运行工况Fig.7 vehicle operation condition

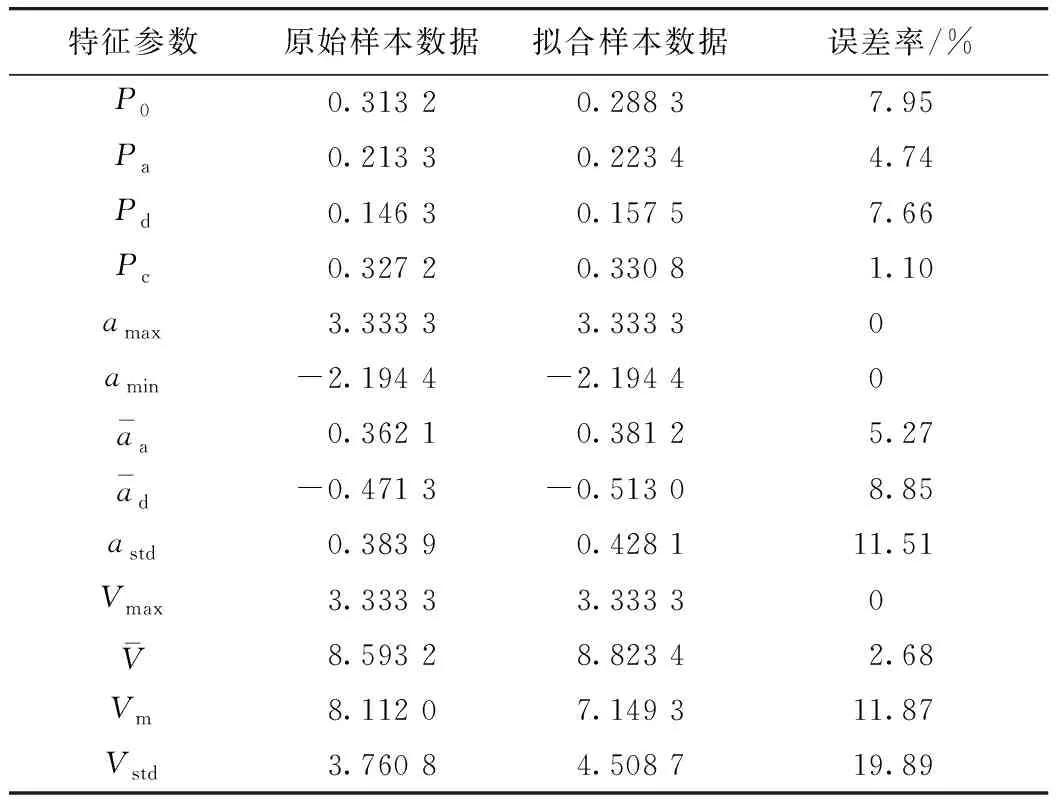
表11 拟合误差分析表Tab.11 Analysis of fitting error

4 结论

本研究选取不同的方法对采集到的车辆的3段行驶数据进行预处理并进行运动学片段划分，从中选取13个特征参数以代表运动学片段的信息，并建立PCA和K-means模型对特征参数进行降维，将数据进行分组聚类。不断提取离聚类中心最近的(即相似度最高的)运动学片段以实现汽车运行工况的构建。最后将拟合工况的各个特征参数值与原始数据的工况参数值进行对比，误差较小，工况拟合效果很好。进而得到以下结论：

(1)本研究的汽车运行工况构建方法可以有效地提取汽车行驶信息，有助于构建汽车运行工况，得到的汽车工况误差很小，优于学界大部分方法，对建立我国符合特定城市的交通状况及实际运乘条件的汽车性能与燃油排放控制的研究提供了一定的参考。

(2)从最终拟合的运行工况不难看出，我国运行工况的怠速阶段时间明显高于欧美国家的工况，欧洲工况具有较少的怠速运行时间[19]。所以若用欧美国家[20-21]的汽车油耗量与污染物排放量的标准来制订我国的污染控制策略并不符合实际国情。建议结合自身情况，建立符合我国道路的汽车运行工况。

但由于时间的关系，没有尝试使用其他模型去拟合运行工况[22]，后续可以尝试马尔可夫法、小波变化法、SOM神经网络模型等方法去改进现有的算法，这样有可能更有效地构建汽车运行工况，而目前采用的方法也可较为准确地构建汽车运行工况。