围岩蠕变对运营隧道衬砌安全性的影响
钱文喜,耿大新,梁国卿
(1. 江西省公路工程有限责任公司,江西 南昌 330006;2. 华东交通大学 土木建筑学院,江西 南昌 330013;3. 江西省天驰高速科技发展有限公司,江西 南昌 330103)
0 引言
公路隧道围岩极其复杂的非线性、各向异性和随时间变化的力学属性,决定了围岩与衬砌结构相互作用的复杂性。在软弱围岩隧道运营期间,二次衬砌与围岩可以同时作为承载主体,而围岩蠕变对隧道稳定性及衬砌结构安全性具有重要的影响。因此,许多学者开展了相关研究:刘甲荣等[1]考虑围岩蠕变效应,分析了不同埋深及偏压条件下衬砌结构表面拉、压应变与损伤值之间的关系;李建军等[2]基于Burgers模型分析了围岩蠕变作用对衬砌结构内力的影响;王迎超等[3]基于广义Kelvin模型分析了不同时机支护下衬砌结构的受力规律;徐国文等[4]建立锚杆-围岩复合体流变模型分析了围岩蠕变作用对裂损衬砌长期安全性的影响;Guan等[5-6]通过对Ureshino隧道进行跟踪监测,分析了围岩蠕变与隧道持续变形的关系;王中文等[7]考虑隧道围岩的蠕变特性,利用初衬变形理论公式分析了隧道初衬最终变形及二次衬砌合理的支护时机;唐葭等[8]基于Burgers模型推导出了考虑围岩蠕变效应的围岩抗力系数公式,进而分析了红砂岩隧道围岩的抗力系数;Fan等[9]采用室内模型试验对泥质软岩隧道围岩的蠕变力学行为进行了研究。此外,左昌群等[10]考虑软弱围岩蠕变特性,分析了不同支护形式下围岩与初期支护结构的相互作用;文献[11-14]对软岩隧道围岩的蠕变特性、蠕变模型及蠕变参数进行了大量研究。
目前,常用的模拟隧道围岩蠕变的元件组合模型有Kelvin模型、西原模型、Burgers模型、Bingham模型等[15]。但不同地区、不同类别的岩石力学性状差异较大,需要选择适用的元件组合模型来描述岩石的蠕变特性。本研究以江西九景高速公路隧道为依托,基于该隧道Ⅳ级围岩区段泥质粉砂岩蠕变试验结果,利用Cvisc黏弹塑性模型对其蠕变模型及参数进行辨识,进而分析围岩蠕变效应对运营隧道衬砌结构安全性的影响,以期为公路隧道运营期的管理和养护提供参考。
1 工程概况
九景高速公路隧道为双向两车道,隧道净宽10.25 m,净高7.425 m,洞身衬砌采用三心圆曲墙式,运营时间已超过10 a。洞身穿越地层岩性主要为泥盆系细砂岩和志留系粉砂岩,岩体完整性以较完整~较破碎为主。其中,Ⅳ级围岩隧道断面如图1所示。
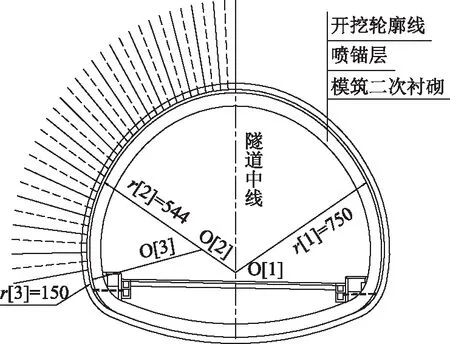
图1 Ⅳ级围岩复合式衬砌Fig.1 Composite lining of Grade IV surrounding rock
2 砂岩蠕变模型辨识
2.1 蠕变试验
通过单轴抗压强度试验,获得了5组φ50×100 mm 圆柱体岩样破坏时最大轴向压力Pi和抗压强度Rci(见表1),其中,i=1,2,…,5。岩样取自九景高速公路隧道,为泥质粉砂岩,无明显层理,且节理裂隙不发育。
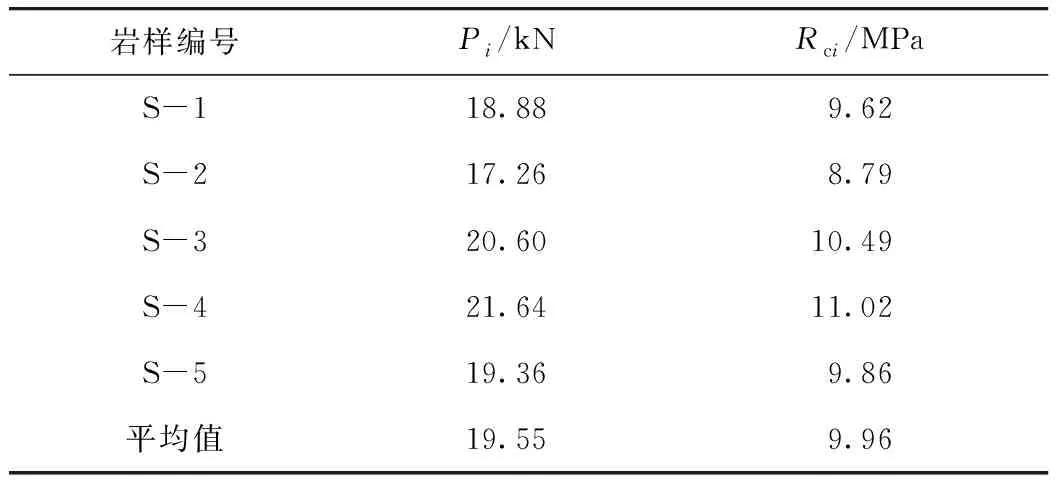
表1 泥质粉砂岩单轴抗压强度Tab.1 Uniaxial compressive strength of argillaceous siltstone
通过YSR-300型岩石三轴蠕变试验系统对泥质粉砂岩进行单轴压缩蠕变试验,获得了岩样在0.7Rc,0.8Rc,0.9Rc应力水平下较能反映其蠕变特性的试验数据曲线(见图2)。
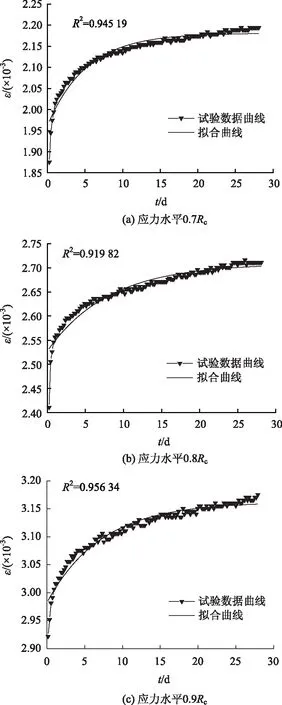
图2 不同应力水平下的非线性拟合结果Fig.2 Nonlinear fitting results at different stress levels
2.2 蠕变模型与参数确定
Cvisc模型由Kelvin体、Maxwell体和塑性体共同构成(见图3)。当应力水平较低时,变形速率逐渐减小进入衰减蠕变阶段,之后逐渐趋于某一恒定值进入稳定蠕变阶段;当应力水平等于或超过某一临界应力值σs后,逐渐转化为加速蠕变过程。
在一维应力状态下,Cvisc模型蠕变本构方程为:
(1)当σ<σs时,
(1)
(2)当σ≥σs时,
(2)
式中,EK、EM分别为Kelvin体、Maxwell体的弹性模量;ηK、ηM分别为Kelvin体、Maxwell体的黏性系数;σ0为常应力;εP为塑性体应变。

图3 Cvisc模型Fig.3 Cvisc model
蠕变方程(1),(2)属于非线性函数形式,为求其中的蠕变参数,可采用最小二乘法中Boltzmann法处理试验数据,即采用线性叠加的间接方法求解[16]。结果表明,图2中的拟合曲线与试验数据曲线的相关系数R2在0.92~0.96之间,因此,可以认为Cvisc模型能够描述泥质粉砂岩的衰减蠕变和稳定蠕变关系。根据室内蠕变试验结果,得到Cvisc模型在0.7Rc,0.8Rc,0.9Rc应力水平下的蠕变参数(见表2)。
3 数值模拟与结果分析
3.1 模型建立
以Ⅳ级围岩公路隧道衬砌结构为研究对象,利用FLAC3D建立两车道公路隧道三维数值模型,如图4所示。隧道模型左、右侧均距离隧道中心线50 m(约4倍隧道开挖跨度),洞周拱顶以上取24 m,仰拱以下取36 m,纵向取60 m。围岩采用实体单元模拟,本构模型采用Mohr-Coulomb模型,初始地应力场仅考虑重力作用。此时,边界条件采用位移约束,即左右两侧采用水平位移约束,顶部自由无约束,底部采用竖向位移约束。

表2 Cvisc模型参数Tab.2 Parameters of Cvisc model

图4 三维隧道数值模型Fig.4 3D tunnel numerical model
在隧道施工期间,假定围岩在开挖条件下的变形完全为弹性或同时含有塑性变形。因此,Cvisc模型中用以描述围岩时效变形的黏性元件应不发生作用,围岩变形仅由模型中的弹性或塑性元件来体现,故此时蠕变方程(1)、(2)中的t=0。于是,通过命令(SET CREEP OFF)来屏蔽蠕变模型的时效作用,即仅对围岩进行静力计算分析。其中,Ⅳ级围岩的物理力学参数见表3。

表3 围岩物理力学参数Tab.3 Physical and mechanical parameters of surrounding rock
通过提高洞周围岩变形模量、黏聚力等指标的方法来模拟锚杆加固区的力学行为,加固区厚度取4 m,Ⅳ级围岩锚杆加固区域的物理力学参数见表4。
假定围岩与初期支护分担60%释放荷载,二次衬砌分担40%释放荷载。于是,在施加衬砌前,对隧道周边围岩进行某一比例卸荷,即选定应力释放

表4 锚杆加固区围岩物理力学参数Tab.4 Physical and mechanical parameters of surrounding rock in anchor reinforcement area
率λ=0.6。采用实体单元模拟喷混凝土层,本构模型采用线弹性模型;二次衬砌采用衬砌结构单元(Liner)模拟,初期支护的物理力学参数见表5。

表5 初期支护物理力学参数Tab.5 Physical and mechanical parameters of initial support
考虑到喷混凝土层与二次衬砌之间防水层的影响,单元界面接触参数选取见表6。

表6 单元界面接触参数Tab.6 Contact parameters of unit interface
在隧道运营期间,假定围岩总变形由开挖导致的弹塑性变形和蠕变变形共同构成。因此,Cvisc模型中用以描述围岩时效变形的黏性元件开始发生作用。于是,基于静力计算分析结果,通过命令(SET CREEP ON)来开启蠕变模型的时效作用,即对围岩进行蠕变计算分析。其中,Cvisc模型所需的Mohr-Coulomb强度参数见表7。对泥质粉砂岩在0.7Rc,0.8Rc,0.9Rc应力水平下的蠕变参数进行平均值计算,得到围岩蠕变参数。

表7 围岩蠕变参数Tab.7 Creep parameters of surrounding rock
Cvisc模型的最大蠕变时间步长为:
(3)
为了使计算模型更好地收敛,设置蠕变计算时间步长为2.5×10-3,最大蠕变时间步长为5.0×10-3,最小蠕变时间步长为5.0×10-4。将蠕变计算总历时定为3 650 d(即蠕变计算的总历时为10 a)[17]。
3.2 结果分析
我国《公路隧道设计规范》[18](JTG3370.1—2018)规定,公路隧道支护结构需满足验算的安全系数要求。规范规定混凝土偏心受压构件的抗压和抗拉强度验算需满足式(4)和式(5)。
KcN≤φαRαbh,
(4)
(5)

在隧道运营10 a过程中,单考虑围岩蠕变作用,将数值模拟的计算结果代入式(4)和式(5)得到二次衬砌拱顶、拱肩和拱腰位置安全系数随时间的变化曲线(见图5)。从图中可以看出,随着二次衬砌服役时间的增加,拱顶、拱肩和拱腰位置安全系数总体呈逐渐减小的趋势,其中拱顶处安全系数降低最为显著,表明围岩蠕变变形压力随着时间逐渐增加。

图5 衬砌结构安全系数随时间变化曲线Fig.5 Curves of lining structural safety factor varying with time
隧道运营10 a后,二次衬砌轴力、弯矩、安全系数的分布,见图6~图8。从图中可以看出,衬砌结构最大轴力出现在边墙位置,为2 700 kN,并沿拱顶和拱底位置环向减小,最小轴力出现在拱底位置,为757 kN;最大正弯矩出现在拱脚位置附近,为312 kN·m,最大负弯矩出现在拱底位置,为40.9 kN·m;安全系数最小值出现在边墙位置,为2.9,最大安全系数出现在仰拱底位置,为72.3。这表明,在同一支护时间,二次衬砌支护结构承载较小的位置(即安全系数较高的位置),围岩的蠕变变形量较大,因而支护结构承受的围岩压力相对较小,但过小的支护承载又会导致围岩蠕变变形而增加围岩压力,进而不利于衬砌结构的长期安全。

图6 衬砌结构轴力(单位: kN)Fig.6 Axial force of lining structure(unit:kN)

图7 衬砌结构弯矩(单位: kN·m)Fig.7 Moment of lining structure(unit:kN·m)
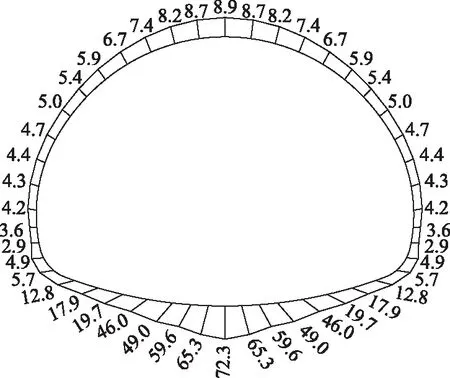
图8 衬砌结构安全系数Fig.8 Safety factor of lining structure
3.3 隧道埋深的影响分析
在隧道运营10 a过程中,考虑围岩蠕变作用,在11.7 m(hq),23.4 m(2hq),35.1 m(3hq),46.8 m(4hq)的隧道埋深下,将数值模拟的计算结果代入式(4)和式(5)得到二次衬砌拱顶、拱肩、拱腰位置的安全系数随其服役时间的变化曲线(见图9)。从图中可以看出,在围岩蠕变变形压力作用下,随着隧道埋深的增加,衬砌结构拱顶、拱肩、拱腰位置在同一服役年限的安全系数逐渐增大,其中拱顶位置的增长幅度最大。这表明,在同一支护时间,二次衬砌支护结构的承载随着隧道埋深的增加而减小,即围岩自身承担了较大部分的因蠕变变形而增加的围岩压力,从而对二次衬砌的长期安全有利。
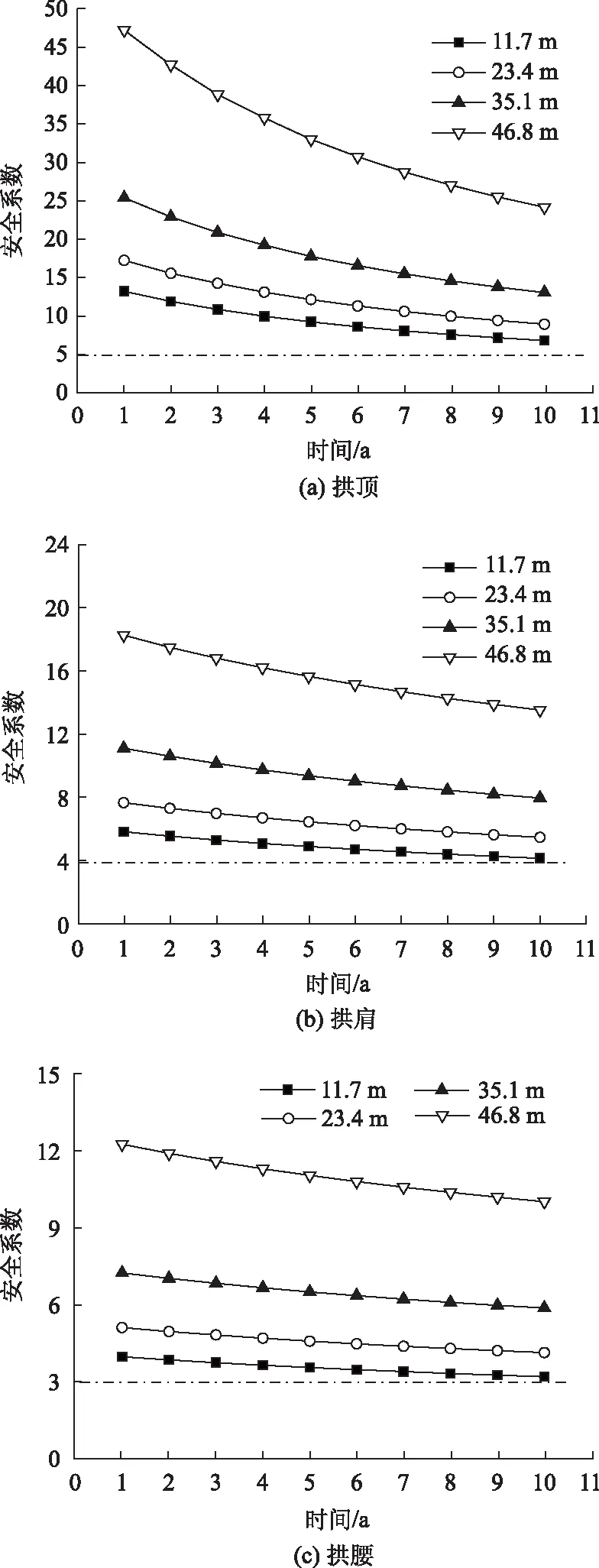
图9 不同埋深下衬砌安全系数随时间变化曲线Fig.9 Curves of lining safety factor varying with time under different depths
4 结论
以九景高速公路隧道为背景,利用有限差分软件FLAC3D建立了两车道公路隧道三维数值模型,考虑了围岩蠕变作用,对Ⅳ级围岩公路隧道在10 a运营期间衬砌结构的安全性进行了分析,得出以下结论:
(1)通过对泥质粉砂岩进行单轴压缩蠕变试验,并对试验数据曲线进行非线性拟合。结果表明,其相关系数R2在0.92~0.96之间,可认为Cvisc模型能够很好地描述泥质粉砂岩的衰减蠕变和稳定蠕变关系。
(2)单考虑围岩蠕变作用,在同一支护时间,二次衬砌安全系数较高的位置,支护结构承受的围岩压力相对较小,围岩的蠕变变形量较大,但过小的支护承载又会导致围岩蠕变变形而增加围岩压力,进而不利于运营隧道衬砌结构的长期安全。
(3)同时考虑隧道埋深的影响,在同一支护时间,二次衬砌支护结构的承载随着隧道埋深的增加而减小,即围岩能够承担较大部分的因蠕变变形而增加的围岩压力,从而对运营隧道衬砌结构的长期安全有利。

