SEC 模型在高考中的应用与反思
田 霖 韦小满
考试内容及命题方式改革是新一轮高考改革的重要方面。 2014 年,《国务院关于深化考试招生制度改革的实施意见》提出,要深化高考考试内容改革,依据高校人才选拔要求和国家课程标准, 科学设计命题内容[1]。 2019 年,《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》进一步提出,要深化考试命题改革, 高等学校招生全国统一考试(简称 “高考”)命题要以普通高中课程标准和高校人才选拔要求为依据, 实施普通高中新课程的省份不再制定考试大纲[2]。 此前,考试大纲作为高考命题的规范性文件和标准,是考试评价、复习备考的依据;各分省命题省份依据考试大纲, 结合本地高考方案和教学实际制定考试说明, 对考试大纲做进一步细化、补充,考试说明也是命题和备考的重要参考。 取消考试大纲意味着考试说明也将一同取消, 高考命题将回归课程标准。 此时,高考与课程标准的一致性就成为衡量高考质量的重要指标, 试卷与课程标准的一致性也成为研究者关注的热点。
一致性是指考试与课程标准内容要求的吻合程度。 国家课程标准是教材编写、教学、评估和考试命题的依据[3],以课程标准作为依据进行命题,可以确保 “所考即所学”,保障考生对于考查内容拥有平等的学习机会,这既是有效测量的要求,也是考试公平的要求。 国际上广泛使用的考试与课程标准一致性研究工具主要有 “韦伯模型”“课程实施调查的模型(简称 SEC 模型)” 及 “成功分析模型” 等,其中 SEC模型作为一种定量分析模型, 提出了一致性量化指标,应用较广。 美国联邦政府和十几个地方州市都采用了SEC 模型分析考试与课程标准的一致性[4]。 SEC模型为高考试卷与课程标准的一致性研究提供了参考,本研究以高考数学试卷为例,对SEC 模型在高考中的应用进行探讨与反思。
一、SEC 模型概述
SEC 模型的全称为 “课程实施的调查模型(Survey of Enacted Curriculum Model)”,由美国威斯康辛教育中心研究人员安德鲁·波特 (Andrew Porter)和约翰·史密森(John Smithson)等人于 1999 年提出,用于判断评价项目与课程标准的一致性。 SEC 模型通过建立通用矩阵的方式分析课程标准、课程、评价及教学之间的一致性, 其中关于评价与课程标准的一致性有助于深入理解考试与课程标准之间的本质关系[5]。 SEC 模型借鉴了韦伯模型中的一致性分析维度及其判断标准, 提出知识广度与知识深度的一致性是衡量考试与课程标准一致性的最直接的、 也是最核心的指标。 SEC 模型的一致性研究过程主要包括三个步骤:首先,建立分析框架,具体是指由知识主题与认知层次要求构成的二维矩阵, 这也作为编码框架;第二,对课程标准和试卷分别进行认知层次要求编码, 基于分析框架分别形成课程标准与试卷的知识主题分类与认知层次要求分布的矩阵数据,矩阵中的单元格为知识主题数量比率或试题分值比率;第三,根据课程标准与试卷的矩阵数据计算波特一致性系数(简称 “一致性系数”),衡量试卷与课程标准的吻合程度[6]。 SEC 模型提出的波特一致性系数为一致性研究提供了清晰简明的量化指标, 其具体计算公式如下:
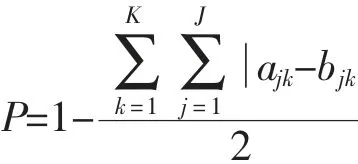
式中P 代表波特一致性系数,J 代表矩阵表格的行数,K 代表矩阵表格的列数,ajk与bjk分别代表两个矩阵表格a、b 中第j 行与k 列对应的单元格数值(比率)。 P 的取值范围是 0 到 1,P=0 表示试卷与课程标准的一致性最差,即完全不一致;P=1 表示试卷与课程标准在知识主题及认知层次要求分布上完全一致[7]。
二、基于SEC 模型的实证研究
(一)研究资料
以A 省2016 年高考数学(理科)试卷为例开展实证研究①A 省目前实行高考分省命题,由于2017 年版课程标准发布以来A 省基于该版本课程标准的高考命题还未开始,2017 年至2019 年A 省高考命题采用过渡版本的课程标准。鉴于此,本研究选择A 省2016 年试卷为例开展实证研究。。 A 省2016 年高考实行分省命题, 采用2003 年版《普通高中数学课程标准(实验)》(简称《数学课标》),A 省根据当年考试大纲、结合本省教学实际制定了数学科目考试说明(简称《考试说明》),作为高考命题的直接依据。 研究资料包括《数学课标》、A 省 2016 年高考数学(理科)试卷(简称“数学试卷”)、《考试说明》。 数学试卷的题量为 20 题,满分值为150 分,考试时长为120 分钟,包括选择题、填空题、解答题三种题型。
(二)研究工具
采用SEC 模型进行资料编码及一致性分析。 本研究主要关注试卷考查的知识主题以及认知层次要求两个方面,SEC 模型中的 “知识主题和认知层次要求” 二维编码矩阵与本研究相符。
(三)研究过程
1. 建立编码框架
采用SEC 模型通用编码框架 “知识主题×认知层次要求” 二维矩阵制定本研究的编码框架。 首先要确定知识主题分类,本研究根据《数学课标》中的必修课程及选修课程知识主题,结合《考试说明》要求及A 省教学实际,去除不在考查范围内的知识主题,最终纳入编码框架23 个知识主题, 按照知识主题在《数学课标》中的自然顺序依次编号,具体见表1。 其次要确定认知层次要求等级,《数学课标》 将认知层次要求划分为 “知道/了解/模仿”“理解/独立操作”“掌握/应用/迁移” 三个等级,《考试说明》将认知层次要求划分为 “了解”“理解”“掌握” 三个等级,二者认知层次要求等级划分相似, 只是列举的行为动词数量有所不同。 为了便于表述,本研究将认知层次要求统一界定为 “了解”“理解”“掌握” 三个层次,分别编码为A、B、C,三个认知层次要求逐级提升。 三个认知层次要求对应的《数学课标》中使用的行为动词分别是:了解——了解,体会,知道,识别,感知,认识,初步了解,初步体会,初步学会,初步理解,求,等;理解——描述,说明,表达,表述,表示,刻画,解释,推测,想像,理解,归纳,总结,抽象,提取,比较,对比,判定,判断,会求,能,运用,初步应用,初步讨论,等;掌握——掌握、导出、分析,推导、证明,研究、讨论、选择、决策,解决问题,等。 根据知识主题分类以及认知层次要求等级,建立 “23(知识主题)×3(认知层次要求)” 的表格矩阵作为本研究的编码框架,具体见表1。
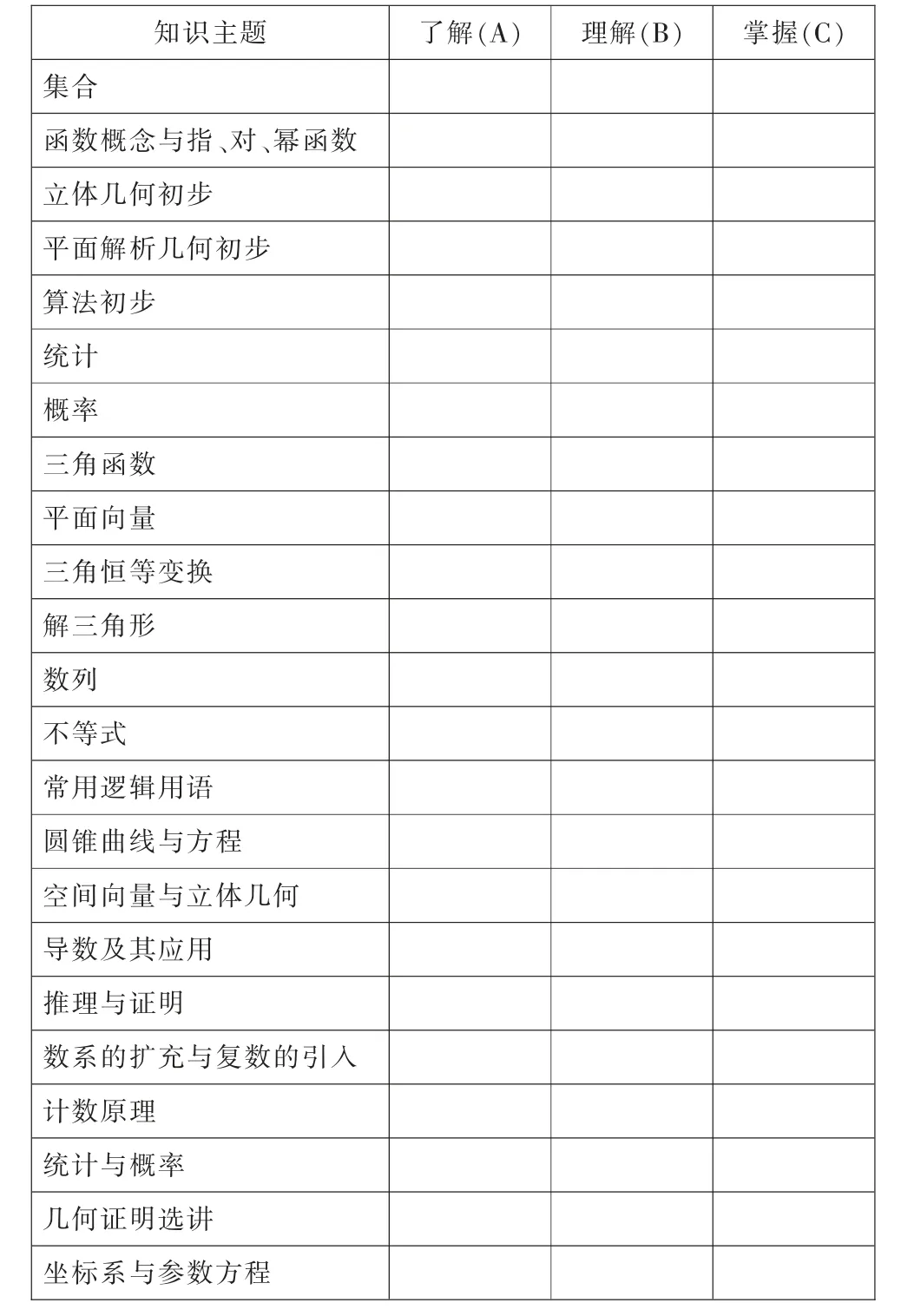
表1 一致性研究编码框架
2. 对《数学课标》编码
根据编码框架,采用23×3 矩阵对《数学课标》进行编码。 认知层次要求针对的是具体知识点(即《数学课标》或《考试说明》中的三级知识主题),具体知识点划分以A 省《考试说明》规定为准,本研究共涉及23 个知识主题162 个知识点。 本研究邀请1 位具有15 年以上高考数学命题经验的学科专家(副研究员职称) 和1 位具有数学学科背景的教育测量与评价专家(副研究员职称)担任编码员。 首先,编码员根据《数学课标》中各知识点描述所采用的行为动词,对162 个知识点依次进行认知层次要求独立编码,二人编码结果的斯皮尔曼等级相关系数为0.961(N=162,p<0.01);然后,二人针对编码分歧进行讨论,最终对所有知识点认知层次要求编码达成一致意见,作为最终编码结果(限于篇幅,162 个具体知识点及其认知层次要求编码不在文中具体呈现)。 完成162个知识点认知层次要求编码后, 将编码结果汇总至23×3 矩阵中,具体见表 2。
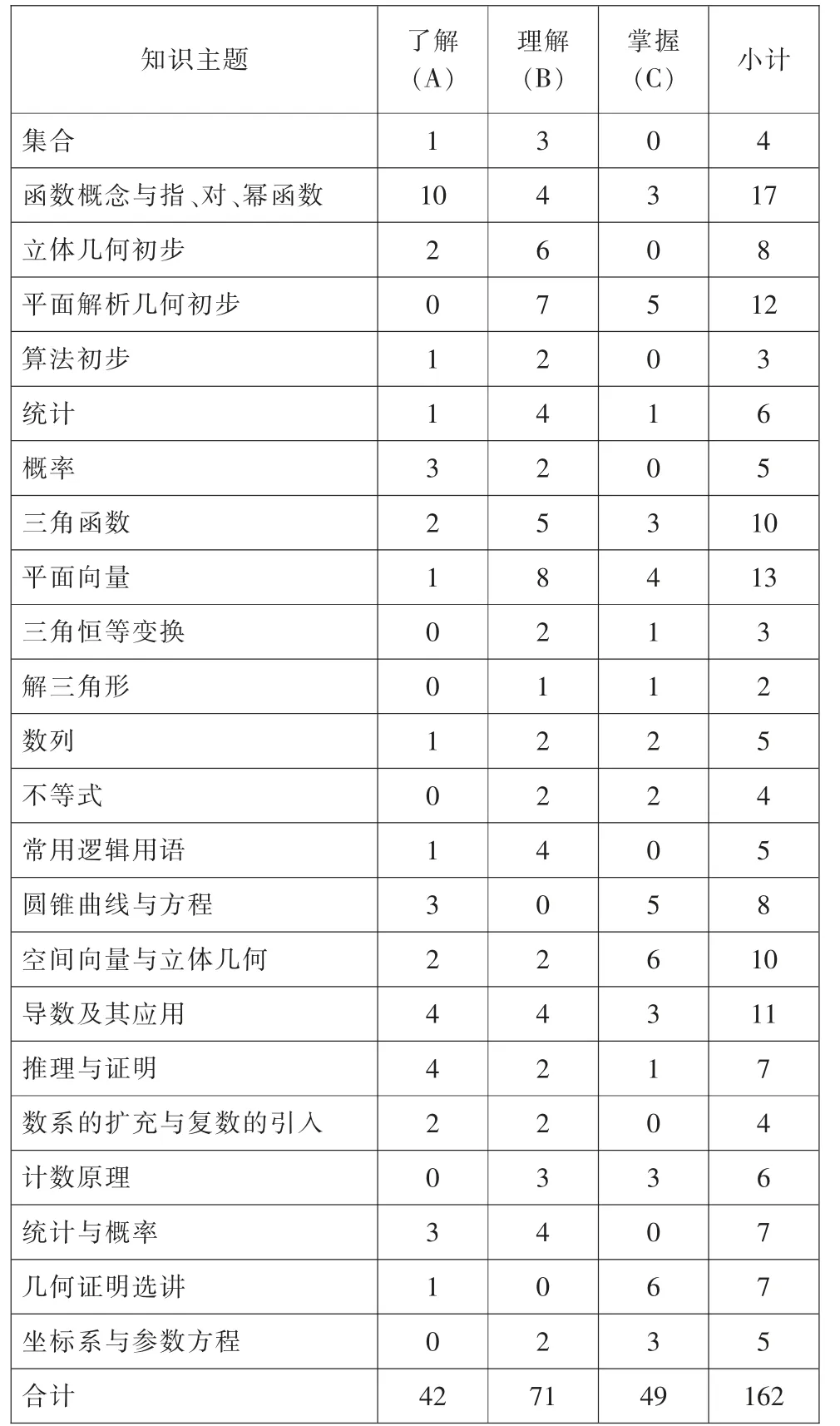
表2 《数学课标》知识主题及认知层次要求编码(数量)
为了与数学试卷的编码矩阵进行比较, 对上述矩阵进行转化处理, 根据数量分布计算各单元格数量比率,结果见表3。

表3 《数学课标》知识主题及认知层次要求编码(比率)
3. 对数学试卷编码
根据编码框架,采用23×3 矩阵对数学试卷进行编码,编码员同《数学课标》编码员。 首先,两位编码员共同对试卷考查的知识主题进行判断, 确定该试卷主要考查了22 个知识主题、40 个知识点,并结合试题满分值、考查主题权重进行分值分配;然后,编码员独立对试题考查知识点进行认知层次要求编码,二人编码结果的斯皮尔曼等级相关系数为0.947(N=40,p<0.01);最后,两位编码员对编码分歧进行讨论,最终达成一致意见。 需要说明的是,一个试题可能同时考查多个不同的知识点, 对不同知识点的认知层次要求也可能不同, 需要根据试题实际考查的知识点及认知层次要求分别进行编码; 不同试题可能考查同一个知识点, 需要按照知识点所属的知识主题进行认知层次要求编码汇总。 完成对试卷全部试题认知层次要求编码后, 按知识主题分类汇总各认知层次要求下的试题分值, 将汇总结果分配到23×3 矩阵中,具体见表 4。
为了与《数学课标》的编码矩阵进行比较,同样对上述矩阵进行转化处理, 根据分值分布计算各单元格分值比率,结果见表5。
(四)研究结果
在SEC 模型中, 需要通过模拟数据获得一致性系数显著性参考值[8],本研究采用R 语言软件模拟数据获得一致性系数显著性参考值。在R 语言软件中,运用均匀随机数生成器runif()函数进行数据模拟,将编码框架涉及的162 个知识点随机分配到表1 所示的23×3 矩阵中;然后进行转化处理,将矩阵中各单元格数值以比率形式呈现, 所获矩阵各单元数值总和是1。 将数学试卷满分值150 分也随机分配到表 1 所示的 “23×3” 矩阵中,同样进行转化处理。 然后, 利用一致性系数公式计算前述两个随机矩阵的一致性系数P。 将上述过程在R 语言软件中循环计算20000 次,可获得一致性系数P 值的正态分布,其在0.05 水平显著的参考值为0.6987。 即在《数学课标》与数学试卷随机一致性系数的正态分布中,要达到0.05 水平统计学意义上的显著一致性,在知识主题为23 个、 认知层次要求等级为3 个、 知识点为162 个、试卷总分值为150 分的情况下,一致性系数需要达到0.6987 及以上。

表4 数学试卷考查知识主题及认知层次要求分布结果(分值)
确定一致性系数显著性参考值后, 计算本研究中的数学试卷与《数学课标》的一致性系数,将表3和表5 中的数据代入一致性系数计算公式中, 得到P 值为 0.3306,P 值小于 0.6987,并未达到 0.05 水平的显著性参考值。 研究结果表明,A 省2016 年高考数学(理科)试卷与《数学课标》的一致性程度较低,二者不具有统计学意义上的显著一致性。
三、讨论与反思
SEC 模型一致性系数不显著能否作为否定试卷与课程标准相吻合的充分证据? 是否反映试卷偏离课程标准、 内容效度较低? 对高考命题实践有何启发? 这些问题需要进一步讨论和反思。
(一)波特一致性系数的适用性
通常高考命题会依据课程标准、 考试大纲及考试说明等规定性文件制定命题蓝图与双向细目表,来确保试卷构念代表性, 从这个角度而言高考试卷应该与课程标准相一致。 例如, 本研究中A 省规定《数学课标》23 个知识主题纳入考查范围,数学试卷考查了22 个知识主题,试卷覆盖率为95.7%。 因此,虽然本研究中试卷与《数学课标》的一致性系数不显著, 但这不能作为否定试卷与课程标准相吻合的充分证据。 目前,并没有相关理论明确提出我国高考试卷与课程标准存在显著一致性, 且SEC 模型提出的波特一致性系数量化指标是否适用于我国高考领域也尚无定论。 对国内已有的基于SEC 模型的高考与课程标准一致性研究报告进行梳理, 发现高考各科试卷与课程标准的一致性程度表现不一。 其中,高考物理试卷与课程标准一致性系数分布于0.277~0.508 之间,均未达到统计显著性参考值[9];高考化学试卷与课程标准一致性系数分布于0.324~0.524 之间,均未达到统计显著性参考值[10,11];高考政治试卷与课程标准一致性系数为0.448,未达到统计显著性参考值[12];高考语文试卷与课程标准一致性系数为0.717,未达到统计显著性参考值[13];高考生物试卷与课程标准一致性系数分布于0.603~0.705 之间,均未达到统计显著性参考值[14];高考地理试卷与课程标准一致性系数分布于0.300~0.467 之间,均未达到统计显著性参考值[15];已有的基于SEC 模型的实证研究结果都发现, 我国高考各科试卷与课程标准的一致性系数普遍较低, 而且都没有达到统计学意义显著水平。
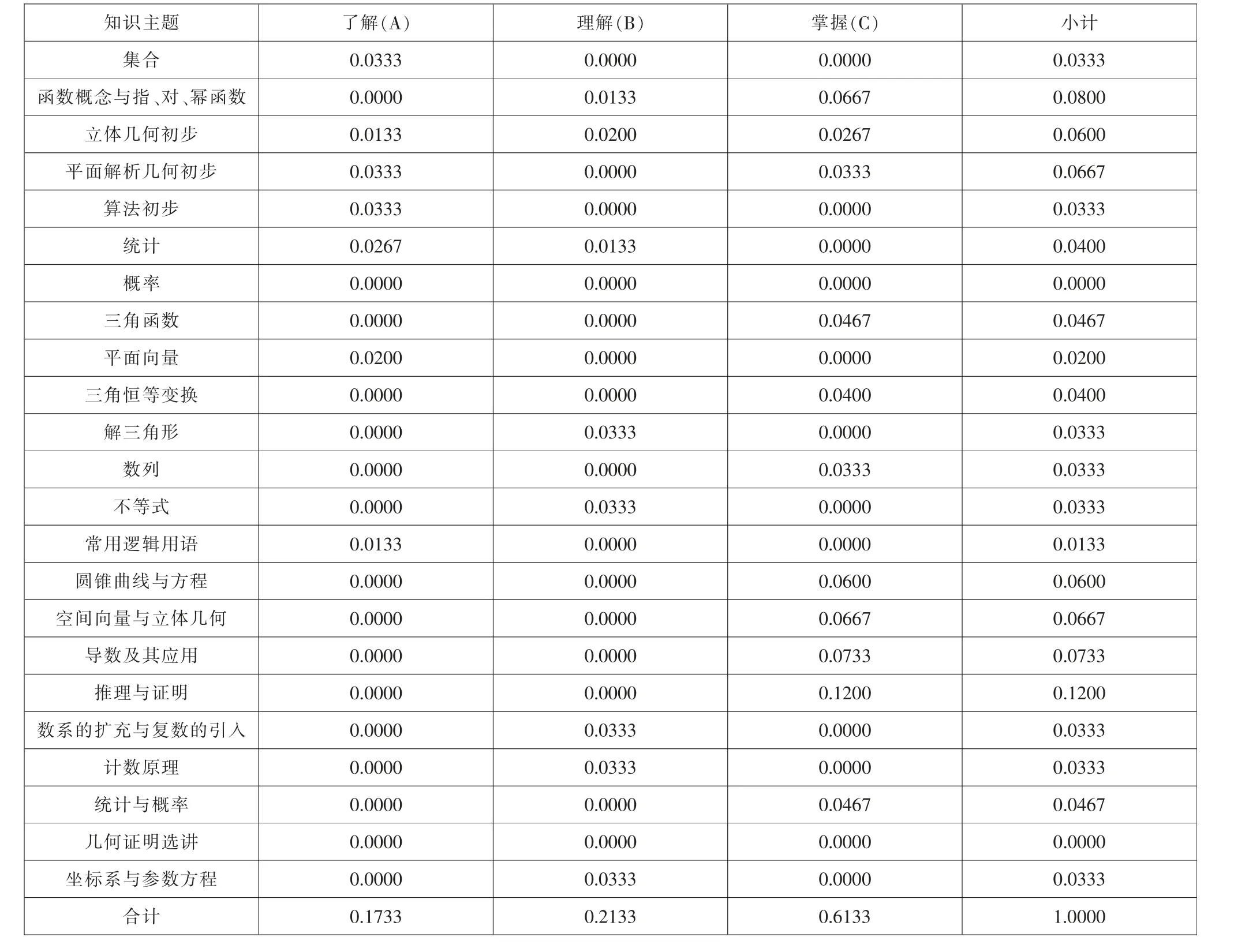
表5 数学试卷考查知识主题及认知层次要求分布结果(分值比率)
高考试卷与课程标准的波特一致性系数不显著,可能存在多种影响因素。 首先,高考试卷强调选拔性, 并不是对普通高中阶段的最低达标者进行筛选,传统的高考命题以考试大纲及考试说明为依据,可能并未追求或强调试卷与课程标准的一致性,造成二者一致性系数较低;其次,SEC 模型中的认知层次要求划分通常采用布鲁姆教育目标分类法, 包括记忆、理解、运用、分析、评价和创造六个层次,而我国普通高中课程标准对认知层次要求的划分并未严格采用布鲁姆教育目标分类法, 且不同学科课程标准之间的认知层次要求划分也存在差异, 例如本研究中的数学试卷认知层次要求划分为了解、理解、掌握三个等级, 这会影响一致性编码框架进而影响一致性系数;第三,一份高考试卷的试题量有限,考查的具体知识点数量及认知层次要求也是有限的,一致性系数可能受到试题量局限的影响;第四,在高考分省命题中, 各省制定的考试说明还可能根据本省教学实际对课程标准中相关知识主题考查要求作出调整, 例如规定本省高考试题考查的知识点认知层次要求高于或低于课程标准, 这也会影响一致性编码框架。鉴于上述原因,本研究认为SEC 模型作为考试与课程标准一致性研究工具在分析思路上具有较高的参考价值, 但该模型提出的一致性系数指标并不一定适用于我国高考领域, 不宜将一致性系数是否显著作为判断高考试卷与课程标准一致程度的唯一标准;研究者应主要关注试卷考查内容覆盖率、试卷考查深度与课程标准的相符程度, 同时参考其他的考试与课程标准一致性研究工具获得的指标。
(二)对高考命题实践的启示
高考作为一种终结性评价活动, 其评价机制的基础是被评价对象(即考生群体)在不同程度上掌握的相关知识或能力。 在这种评价机制中,教学和考试是两个不可或缺的环节, 而这两个环节的连接纽带就是高中课程标准。 在高考改革背景下,命题管理回归课程标准是未来趋势, 如何加快建立适应没有考试大纲或考试说明的命题工作模式、 如何保障高考试卷与课程标准的吻合程度、 如何利用课程标准衔接教学与命题实践, 成为高考命题实践面临的新挑战。 在国务院于2019 年6 月发布文件明确提出我国高考不再编制考试大纲后,教育部考试中心于2020年1 月发布了《高考评价体系》,围绕高考的核心功能、 考试内容和考试要求等关键问题形成系统的理论框架, 旨在建立全面深化高考内容改革的长效机制。 但《高考评价体系》更多的是作为高考内容改革和命题工作的理论依据与实践指南[16],为高考命题提供理论性的、方向性、原则性的指导,命题实践在落实对具体学科知识、能力、素养、核心价值的考查要求时,仍然要以课程标准为根本依据。 我国高考命题采取入闱封闭式管理模式,通常不设置试测环节,无法通过试测数据的统计分析获得试卷/试题参数的量化指标。 一致性分析并不依赖试测数据,命题人员在入闱封闭阶段、 试卷投入使用前就可以通过知识广度与知识深度方面的数据处理完成分析过程,获得试卷质量的量化指标, 进而积累试卷的效度证据。在命题过程中实施试卷与课程标准的一致性分析,能够在试卷投入使用前形成一致性结果反馈,为试题修改提供参考, 尤其对于入闱封闭式管理模式而言这种即时反馈更具实用价值,有利于保障命题质量。
综上, 本研究建议命题管理机构充分重视试卷与课程标准一致性的重要意义, 可结合实际工作条件在命题管理中增设一致性分析环节, 作为一项命题重量保障手段;在一致性分析工具选择方面,建议应综合考虑不同分析模型的优缺点并结合具体学科试卷特点,合理选择使用一种或多种模型;在一致性指标设计方面,建议结合不同学科特点,重在形成有效的、 学科专家充分认可的能够反映试卷与课程标准吻合程度的一个或多个指标, 不必追求某一绝对数量标准, 而要强调指标促进命题活动不断指向高吻合度的方向。 另外,分析框架制定是实施一致性研究的基础和难点,随着2017 年版高中课程标准投入使用,基于新版课程标准的高考命题也逐步启动。 新版课程标准凝练了各学科的核心素养, 明确了学生学习课程后应达成的正确价值观念、 必备品格和关键能力,对知识与技能、过程与方法、情感态度价值观三维目标进行了整合。 以新版课程标准为依据的高考命题实践, 如何在各学科素养体系下建立恰当的一致性分析框架, 将是未来一致性研究要解决的关键问题。

