中小学教师资格考试《语文学科知识与教学能力》试卷质量分析——基于经典测量理论和多元概化理论的视角

杨宏博 罗成禹 杨 卓

一、问题提出

2018 年1 月，中共中央国务院发布了《关于全面深化新时代教师队伍建设改革的意见》。 《意见》是对习近平总书记关于打造 “四有教师” 队伍要求的具体落实，是新时代教师队伍建设的行动指南。 《意见》强调，要完善教师资格考试政策，严格教师准入，提高入职标准，重视思想政治素质和业务能力。 中小学教师资格考试秉承这一宗旨， 致力于考查申请教师资格人员是否具备从事教师职业所必需的教育教学基本素质和能力，以遴选乐教、适教、善教的优秀人才进入教师队伍[1]。

截至2019 年下半年，中小学教师资格考试已经拓展到全国28 个省（市、自治区），累计参加笔试考生2227 万人次，面试考生866 万人次。 中小教师资格考试《语文学科知识与教学能力》（初级中学、高级中学） 是中学类别报考人数最多的科目之一，仅2019 年下半年就有32.3 万人报考。 该科目重点考查申请者四个方面的基本能力[2]，分别是运用语文学科知识的能力、语文教学设计能力、语文教学实施能力和语文教学评价能力。 从测量的角度分析，对《语文学科知识与教学能力》科目的试卷质量进行研究，具有典型参考价值， 有助于完善中小学教师资格考试的科学性以及考查内容和考查策略的合理性。

二、研究工具

1. 经典测量理论

经典测量理论（Classical Test Theory，简称CTT），又称为真分数理论，因其易于被人理解和接受，并且具有较强的适应性， 在20 世纪前叶迅速发展起来。毫无疑问，经典测量理论是体系最成熟的测量理论。它在各行各业测量中的成功应用使其在新的测量理论崛起的今天，仍具有不可替代的地位和作用[3]。 利用经典测量理论，本文统计了2019 年下半年中小学教师资格考试《语文知识与教学能力（初级中学）》科目的148986 份有效笔试试卷（去除零分卷和违纪考卷），全卷平均分为91.5 分，难度为0.61，试卷难度较为合理。 同时，对每一道试题利用经典测量理论进行统计分析，详情如表1 所示。

通过表1 可以发现， 中档题占整份试卷的比例超过80%，区分度优良的题目占比为76%。试卷难度中等，结构合理，区分度较好，具有较高的命题质量。

表1 2019 年下半年《语文知识与教学能力（初级中学）》笔试试卷质量分析

2. 概化理论

当然， 经典测量理论也具有许多不可避免的缺陷和不足，例如不能对测量结果进行推广、模型的若干假设与实际不符等[3]。 相对于考试首次试点以来，一直采用的经典测量理论的质量监测方法， 概化理论（Generalizability Theory，GT）重点讨论考生能力水平与考试题目之间的实质性关系， 能够达到区分考生、评估应考者真实水平的目的，并能较好地控制测评误差。

概化理论的基本原理是运用实验设计的思想，分析影响测验分数差异的各项因素 （如考生个体水平的差异、题目难度等）；并运用方差分析技术，分别估计各因素对分数总变异的贡献 （以方差分量为指标）。 根据不同研究目的的需要，分别考察研究目标在分数总变异中所占的比重。 测量信度的概念在概化理论中用概化系数或可靠性系数来代替[4]。

概化理论用方差分析的方法估计各种方差成分的相对大小，并可直接比较其大小；不仅能估计出主效应，也能估计出交互作用效应，并能对各估计值的大小进行直接比较。 在概化理论中，理论估出各方差成分相对大小的过程，称为概化理论的G 研究。 在G研究的基础上，可通过实验性研究，进一步考察不同测验设计条件下概化系数的变化情况， 如试题容量变化对于概化系数的影响等， 从而寻找最佳的控制误差的方法，作出最佳的设计决策，为改进测验的内容和方式方法提供有价值的信息。 这一阶段称为概化理论的D 研究。

多元概化理论（Multivariate Generalizability Theory，MGT）在概化理论的基础上，深入研究测量目标具有多个全域分数等方面的问题（如总测验可以分解为多个不同维度的分测验）， 主要可应用于测试多门学科或多种能力的综合测验。 近些年来，高考、研究生考试、高等教育自学考试等大规模测验为加强测验信度检验，开始广泛应用这一理论进行研究设计[5-7]。

多年来，虽然山区群众种植核桃的积极性高，但由于重栽轻管、管理粗放，缺乏科学的管理技术。加之山区社会综合发展水平不高，经济基础薄弱、农村外出务工人员增多，农村劳动力减少，农民文化技术素质低、资金投入严重不足等因素阻碍了核桃产业发展。

《语文学科知识与教学能力》是考查考生多种基本素养和能力的综合性测试，根据其考试目标，可以将其分解为多个分测验， 因此对其测验信度进行研究适宜采用多元概化理论的原理和方法。 通过多元概化模型分析中小学教师资格考试 《语文教学知识与能力》 试卷， 探讨各模块及全卷的测量精度 （信度），考察内容模块样本容量变化对考试信度（概化系数）的影响，分析各模块对总测验的贡献率，以期为优化试卷、提高命题质量提供参考。

三、概化理论研究样本

2019 年下半年中小学教师资格考试《语文知识与教学能力 （初级中学）》 科目的全国考生人数为176615（教育部考试中心，2019），从中随机抽取3500份有效试卷（去除零分卷和违纪考卷）。 依据考试大纲，将学科知识、教学设计、教学实施、教学评价四个内容模块作为四个测量分项，分别以V1、V2、V3、V4表示。 试卷总题量为 21 题，满分 150 分。 V1 包括 8题，29 分；V2 包括 2 题，45 分；V3 包括 6 题，52 分；V4 包括 5 道题目，24 分（见表 2）。

本研究将考试的内容设计为四内容因子的单面交叉设计 p×i 多元概化模型， 其中 p 代表考生，i 代表试题。 运用多元概化模型，完成G 研究和D 研究的数据统计与分析；采用Brennan 开发的mGENOVA软件完成多元概化理论相关数据的计算[8，9]。

表2 《语文知识与教学能力（初级中学）》试卷测量内容

四、概化理论研究结果

1. 四因子模型的G 研究

根据理论模型，编写涉及四个分测验的mGENOVA 程序， 分别对整个试卷及四个模块进行G 研究，以估计整个测验和各个模块的测量信度。 同时，利用有关信息评价各个模块对总测验的贡献程度。G研究采用p×i 四因子随机单面交叉设计， 可以得到各效应在四个因子上的方差和协方差变量估计矩阵，如表 3 所示，其中 V1 表示 “学科知识” 模块，V2表示 “教学设计” 模块，V3 表示 “教学实施” 模块，V4表示 “教学评价” 模块。

由表3 可知，V1 相对于其他因子的协方差分量较小，这说明考生在 “学科知识” 模块中的得分高低顺序与他们在其他模块中的顺序不太一致， 即这个模块中的题目在区分考生能力方面功能较弱。 在效应p 上，V2 因子的方差分量最大，而V4 因子的方差分量最低，表明在本次考试中，“教学设计” 模块对考生的区分能力较强，而 “教学评价” 模块对考生的区分能力相对较弱。

2. 四因子模型的D 研究

D 研究采用p×i 四因子随机单面交叉设计，基于G 研究估计的方差与协方差矩阵， 进一步估计考生在四个因子上的全域分数及相应误差项的方差分量，进而估计概化系数与可靠性指数，如表4 所示。

由表4 可知， 四因子中全域分数方差分量从高到低依次为 “教学设计 V2”、 “教学实施 V3”、“学科知识 V1”、 “教学评价 V4”。 考虑到各分量误差方差的因素， 测量信度最高的因子是V2 （概化系数为0.599）。 结果表明本次考试中，“教学设计” 模块的测量信度相对较高。

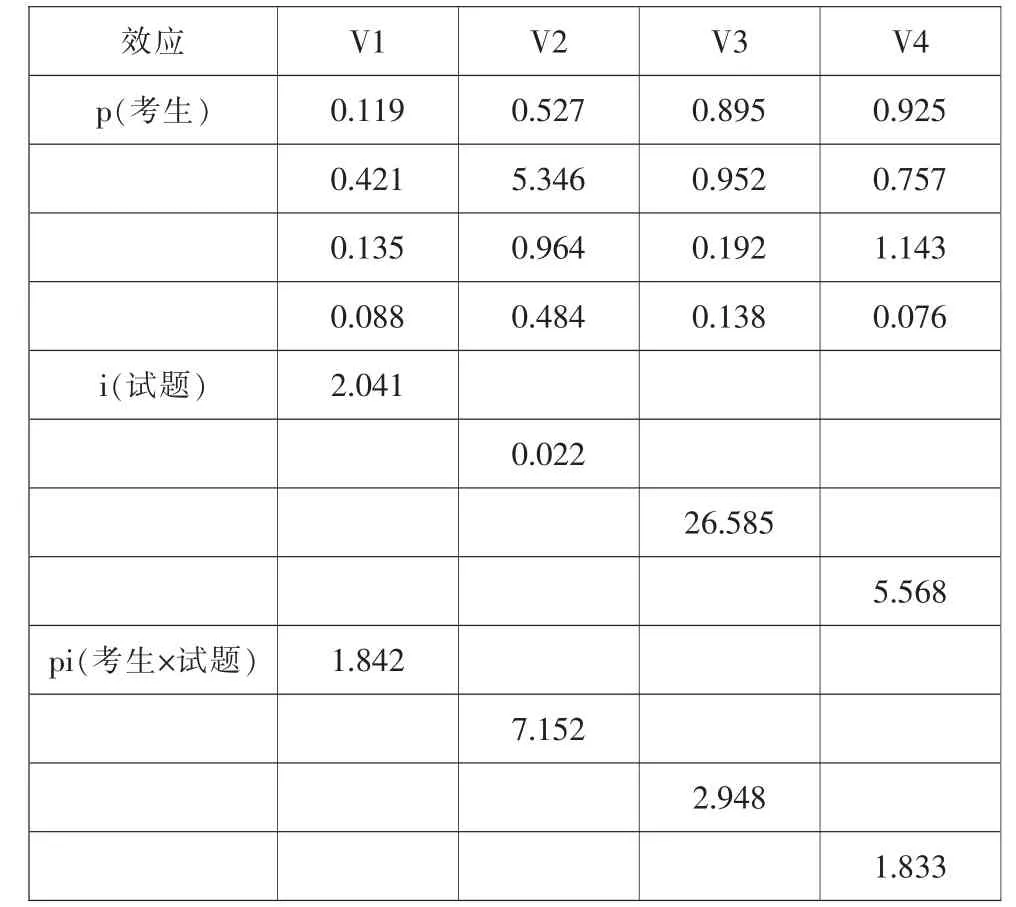
表3 各效应在四因子的方差与协方差分量估计

表4 四因子全域分数各项指标的估计

（2）全域合成分数的测量精度

本研究按照各测量分项试题量所占比例来确定权系数 b，V1 至 V4 四个因子的权系数分别是：0.381，0.095，0.286，0.238。 对四因子全域分数进行合成，可以得到全域总分的方差为0.255，全域合成分数相对误差方差为0.127，全域合成分数绝对误差方差为0.589，进而可计算出全域合成分数的概化系数为0.668，可靠性系数为0.302。

可见， 此次初中语文试卷的总体测量信度较高。 全域合成分数的概化系数较高，而四因子未进行全域分数合成时，各因子全域分数的概化系数及可靠性系数均较低， 在全域分数合成总分后测量精度显著提高，因此对四个分测验的分数进行合成是合理的。

（3）各因子对总方差的贡献比例

为了考察四个分测验对试卷总分方差的实际影响程度， 可使用mGENOVA 程序同时估计出各模块对考试总分方差的实际贡献率（比例），如表5 所示。

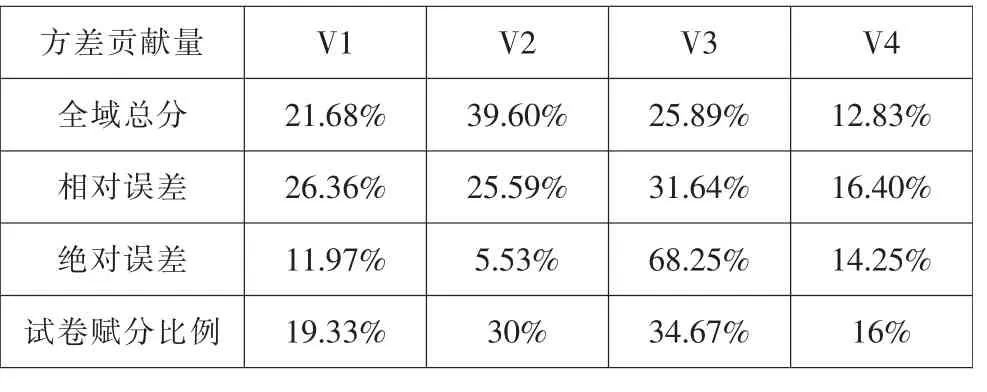
表5 各模块方差贡献比例与试卷赋分比例的比较

由表5 可知，因子V1、V2 对全域总分方差的贡献比例较试卷赋分比例略高，而因子V3、V4 对全域总分方差贡献的比例较试卷赋分比例略低。总体而言，四个因子的总体方差贡献比例与设计的赋分比例较接近，说明各分测验基本达到考试的预期测量目的。

（4）各因子样本容量对测量信度的影响

为了改善测验方法，进一步改进测量信度，本研究考察了各因子样本容量变化对各分测验自身及试卷总分测量信度（采用总分概化系数作为信度指标）的影响情况，如表6 所示。

由表6 可知，当各因子样本容量为2 倍模式时，全域总分的概化系数可增至0.801；当各因子样本容量为3 倍模式时， 全域总分的概化系数可增至0.858。而当各因子的样本容量都减少为1 道题目时，全域总分的概化系数下降至0.425，这样的信度对于教师资格考试这样大规模的国家教育考试是不可接受的。 但是，提高样本容量使题目数量增加为2 倍、3倍时，测量信度将大幅度提高。

当分别固定四因子中的三个因子的样本容量，只变化其中一个因子的样本容量时， 表6 中列出的20 种情况，增加样本容量均能提高测量信度。

由于V1、V3、V4 因子的全域分数误差方差相对较小，因此，提升这几部分的题量对整卷的概化系数的影响并不显著。 V2 因子的全域分数误差方差相对较大，因此，提升这一部分的题量对整卷的概化系数的影响较显著。尤其是当 V2 因子 “教学设计” 题量增至3 题时，总分概化系数增长最为明显。

表6 各因子样本容量与总分概化系数的变化关系

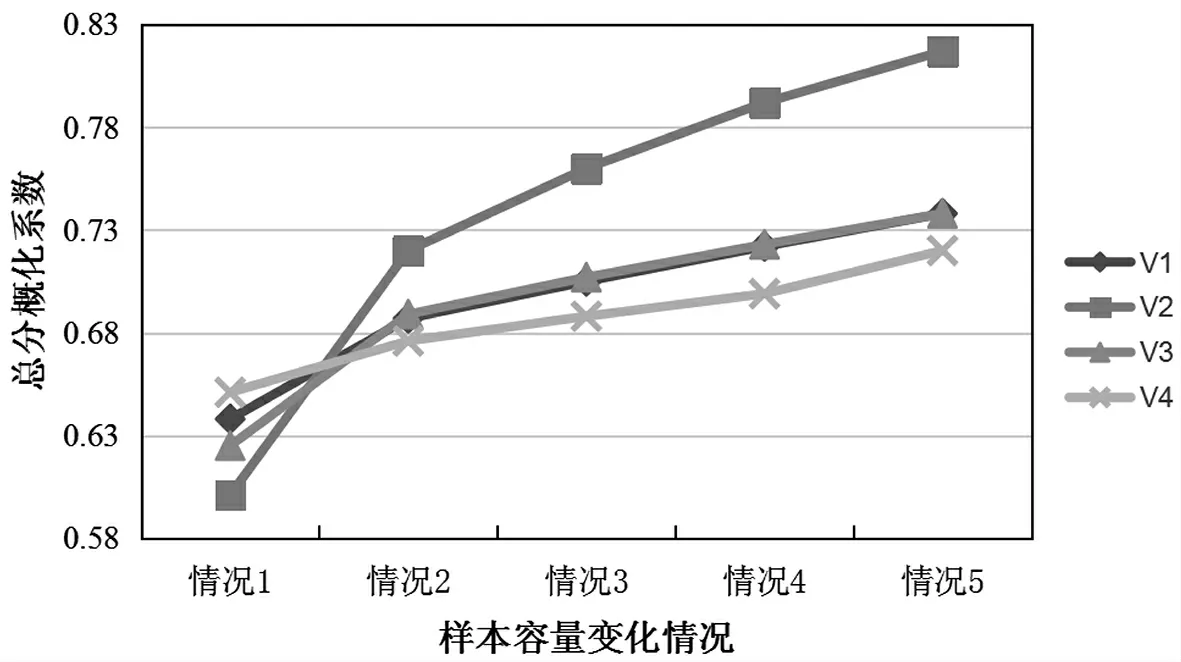
图1 各因子样本容量与总分概化系数的变化关系

五、讨论与结论

通过应用经典测量理论和多元概化理论对2019年下半年《语文学科知识与教学能力（初级中学）》试卷进行分析，可以得到以下结论：

（1）本次考试所使用的试卷质量较好。 试卷总体测量信度属中上水平， 分测验对于全域总分方差的贡献比例与试卷命制时的赋分意图基本一致。

（2） 现行试卷所考查的各个能力模块比重和题量设置比较合理。 尤其是赋分比例最高的 “教学设计” 部分，区分度较强，信度较高，难度适宜（0.6），能够满足对中学语文教师进行选拔的目的和要求。

（3）可尝试通过提高 V2 “教学设计” 分测验的题量来获得更高的测量信度。 若综合考量作答时间等因素的限制， 可考虑减少信度较低的客观题试题数量，或 V4 “教学评价” 分测验的试题数量，同时增加V2 “教学设计” 分测验的试题数量，从而提高全卷的测量信度。

表7 基于CTT“学科知识V1”客观题部分统计分析

结合经典测量理论可以发现，“V1 学科知识” 的选择题第1 题、第2 题、第 15 题难度均在0.8 以上，区分度在0.2 以下（见表7），试题过于简单、区分度较低；而第7 题难度仅为0.16，属于难题，区分度也较低。 可以考虑删除这几道试题，适当提高 “学科知识” 客观题整体难度，增加区分度，从而达到提高测量信度的目的。

六、结语

引入多元概化理论， 对于评价中小学教师资格考试质量提供了更多的角度， 同时提供了有效提高试卷信度的方案。 本文将经典测量理论与多元概化理论相结合， 提供了现有大纲要求的模块结构下的精细化调整方案， 得到了更为准确的试题单题质量和整卷质量改进方案。 今后，可以将多种测量理论结合在一起，形成一套完整、严谨、合理的试卷质量评价模式， 并进一步推广至教师资格考试其他笔试科目的分析和研究，为未来考试大纲的修订提供思路，为政策决策部门提供参考， 不断提升考试的科学化水平，维护国家教育考试的公信力。