基于多特征时空信息融合的行为识别

车维崧，彭书华，李俊杰

(北京信息科技大学 自动化学院，北京 100192)

0 引言

人的行为识别一直是计算机视觉领域中的研究热点。近年来深度神经网络成为处理行为识别问题的主要工具。Tran等[1]最早使用3D卷积网络C3D (convolutional 3D)处理行为识别问题并为此后的研究打下了基础。Hara等[2]系统比较了多种3D卷积网络结构在不同数据集上的表现，发现3D-ResNeXt是当时性能最好的网络结构。但另一方面，3D卷积网络结构的研究总体落后于2D卷积网络，很多性能优秀的二维网络结构在三维领域没有得到充分利用，并且缺乏轻量级的多尺度机制。

随着传感器技术的发展，结构光及飞光(time of flight)摄像头开始快速普及，这类摄像头可以采集被摄物体的深度信息。同时包含RGB及深度视频的多特征数据集开始出现，基于多特征融合的行为识别模型也在快速涌现。许艳等[3]使用通过梯度局部自相关提取的深度信息与通过高斯混合模型及Fisher向量提取的骨架位置进行融合，在基于人工设计特征的方法中取得了较好的效果。黄友文等[4]提出将2D-CNN与LSTM结合用于RGB和光流输入特征的行为识别，并在网络的决策层对两种特征的分类结果进行加权融合，改善了网络性能。基于多特征融合的行为识别方法可以有效去除噪声对各单一模态的影响，提升网络的分类能力。

本文提出了一种新的带有多尺度特征融合层及时空注意力机制的双路径3D卷积网络结构和一种新的加权深度多特征典型相关分析网络。在两个多特征行为数据集上对本文模型进行了实验，证明了该方法的有效性。

1 双路径多尺度时空卷积网络

1.1 双路径时空卷积网络

为保留时间序列信息，循环神经网络引入了隐状态h的概念。为使网络更好地保留完整的时间信息，Chen等[5]提出了广义高阶循环网络：

(1)

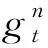
记第t个残差单元的输出为rt，每个残差单元的两个卷积层对应的卷积运算分别记为ft和gt，第一个卷积层的输出记为ht，则：

rt=gt(ft(rt-1))+rt-1

(2)

ht=ft(rt-1)

(3)

(4)

式(4)为广义高阶循环网络形式的残差连接定义式。以同样的方式对密集连接进行分析，3D密集连接的结构如图2所示。

记密集连接单元中两个卷积层分别为gt和ft，单元的输出为

ht=ft(gt([h0,h1,…,ht-1]))

(5)

式中[·]表示按特征维进行拼接。对特征拼接后进行卷积运算等价于分别进行卷积运算后再相加，即：

(6)

为利用两种连接的优势，将残差连接和密集连接两种结构进行拼接可以得到双路径时空卷积单元。将残差连接和密集连接的表达式分别改写为

xt=φt(xt-1)+xt-1

(7)

(8)

则第t个双路径卷积单元的输出为

ht=[xt,yt]

(9)

双路径卷积单元首先将输入特征图分割为两部分，两部分分别通过残差路径和密集连接路径后再进行拼接。由于对输入特征在特征维分割后分别进行卷积与直接对特征进行卷积运算后再进行特征维分割是严格等价的，故其实际结构如图3所示。

1.2 时空多尺度特征融合层

视觉问题与图像或视频的尺寸息息相关，从不同的尺度对特征进行描述会产生不同的效果。在行为识别中由于动作的幅度和持续时间存在差异，在时空网络中加入多尺度方法可以提升网络的分类能力。由于视频样本的规模明显大于图像，在图像领域常见的多尺度金字塔等方法由于显存限制很难直接应用于视频领域。针对现阶段3D卷积网络结构中缺乏轻量级多尺度特征提取方法的问题，本文将二维Rse2Net[6]网络结构三维化并进行了改进，将其作为时空多尺度特征融合层嵌入到3D卷积单元中。

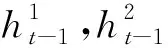
其计算过程用公式表示为

(10)

(11)

式中：*表示卷积运算；Wi为第i组输入特征对应的卷积核。时空多尺度特征融合层除第一组特征不进行卷积直接输出外，其余各组输入均与上一组的输出结果相加后进行卷积运算。第二组到第s组对应的卷积核尺寸均为(3×3×3)，故第一组输入特征对应的感受野范围为1×1×1，第二组为3×3×3，第i组感受野范围为3i-1×3i-1×3i-1。使用时空多尺度特征融合层替代传统卷积单元中间层(3×3×3)卷积后，该层各组输出特征对应的激活区域范围出现了明显差异。最后通过第三层(1×1×1)卷积对不同时空尺度的特征进行非线性组合，使得网络获得更有利于分类的特征表示。

1.3 双路径多尺度时空卷积网络

将前述的双路径、时空多尺度特征融合层和改进的时空注意力机制[7]相结合，组成新的3D卷积网络结构。将其简称为3D-MsDPN(3D multi-scale dual path networks)。该网络的整体结构如图5所示。

网络包含4个时空卷积块，每个卷积块中包含多个时空卷积单元，各时空卷积单元由带有残差和密集连接双路径的3层3D卷积层组成，其中第二层为时空多尺度特征融合层，在第三层卷积层后加入时空注意力机制。网络的最后通过全局池化和激活函数为log softmax的全连接层得到分类输出。

2 深度多特征典型相关分析网络

记第i个输入随机变量对应的深度神经网络非线性变换为fi，则DMCCA的目标是求：

(12)

式中：corr为相关系数；βij为第i和j典型向量在总相关系数中的权重。该权重通过Nelder-Mead方法进行启发式搜索得到。记输入特征Xi对应的神经网络的输出为Hi：

Hi=fi(Xi)

(13)

(14)

(15)

(16)

其中ri为使协方差矩阵非奇异的正则化项。令：

(17)

则Hi和Hj的相关系数为矩阵Tij的核范数。总相关系数即网络训练的损失函数为

(18)

在网络误差梯度反向传播时，记Tij的奇异值分解为UDVT，则损失函数对Hi的偏导数为

(19)

(20)

(21)

DMCCA可以用于特征层级或决策层级的多特征融合。鉴于决策层的特征数目与分类数目相同，采用决策层融合可以减少运算量，并达到与特征层融合相近的结果。在决策层DMCCA融合时，设以灰度、光流和深度视频为输入，分别训练的3D-MsDPN网络的决策层输出为(Yg,Yf,Yd)(Yg,Yf,Yd∈Rn×m，n为样本数目，m为分类的类别数目)，将其按特征维拼接后送入深度多特征典型相关分析网络，该网络为3层全连接结构。记其对应的非线性映射为f，分别计算网络的输出f([Yg,Yf,Yd])∈Rn×m与(Yg,Yf,Yd)的加权相关系数，并以此为损失函数对典型相关分析网络进行训练，最终得到使加权相关系数最大的非线性映射

(22)

式中βi为输入特征对应的权重，通过Nelder-Mead方法启发式搜索获得。在线性特征融合中通过加权可以改善融合效果[10]，在使用典型相关分析进行特征融合时由于各输入特征在分类准确率上存在差异，在总相关系数中对分类准确率高的特征赋予较大权重、对分类准确率较低的特征赋予较小权重同样可以起到改善融合效果的作用。将融合后的输出通过SVM进行分类可以进一步提升分类准确率。上述方法整体结构如图6所示。

3 实验与结果分析

3.1 实验数据集

选择UTD-MHAD[12]和IsoGD[13]两个多特征行为数据集对本文模型进行实验。UTD-MHAD为27分类单人行为数据集，包含861段样本。本文将编号为奇数的实验对象视频作为训练样本，偶数实验对象作为测试样本。IsoGD为249分类单人手势行为数据集，包含47 933段样本，其中有35 878段训练样本、5784段验证样本、6271段测试样本。

3.2 实验环境

CPU：Intel i5-9600K；GPU：RTX2080；显卡运算平台：CUDA 10.1.0；显卡加速库：Cudnn 7.6.0；编程语言：Python 3.6；开发框架：Pytorch 1.3.1。

3.3 视频数据增强

本文提出了一种输入帧速率抖动的视频数据增强方法。记视频样本原始帧速率为ft；由于原始样本存在一定时间冗余，通过实验确定对原始视频时间轴的下采样程度即确定一个最佳网络输入帧速率，记为fh，令k=ft/fh。设置抖动范围L、X为离散随机变量，则第i轮训练时的实际输入帧速率：

(23)

令L=3，X服从-(L-1)/2到(L-1)/2的离散均匀分布。UTD-MHAD数据集ft=30帧/s，经实验确定fh=10帧/s，故每个最小批次的输入样本帧速率在5帧/s、10帧/s和15帧/s中随机抖动。IsoGD数据集ft=10帧/s，实验确定fh=5帧/s，输入样本帧速率在3.33帧/s、5帧/s和10帧/s中随机抖动。

在时间维数据增强的基础上，继续使用了一种视频MixUp增强方法。MixUp[11]通过对两个不同类别的样本和标签进行线性插值来构造新的虚拟样本标签对，以此扩展训练样本的分布，提升网络的泛化能力。此前该方法主要用于图像的数据增强，本文通过实验发现该方法对视频样本同样有效。

3.4 输入及超参数设置

灰度输入：将两数据集RGB视频样本转换为灰度图像序列，输入采用前述输入帧速率抖动和Mixip进行数据增强，依据输入帧速率截取16帧图像序列，采用空间随机剪裁和随机翻转。对于UTD-MHAD数据集样本不进行分辨率压缩直接截取，输入维度为1×16×192×160。对于IsoGD数据集先将视频分辨率压缩到192×144后随机截取128×128窗口，输入维度为1×16×128×128。

光流输入：采用TV-L1方法提取光流。UTD-MHAD数据集样本每隔1帧提取光流，IsoGD数据集提取相邻两帧光流。通过极坐标转换为HSV序列后输入网络。UTD-MHAD光流输入维度为3×16×192×160，IsoGD数据集为3×16×128×128。

深度输入：与灰度输入预处理完全一致。

网络训练采用自适应的Radam(rectified adam)和Lookahead方法结合作为优化器，初始学习率设置为1×10-3，Lookahead机制设置k=5。

3.5 网络结构对比分析

以50层的3D-ResNeXt-50作为基准模型，分别与只加入双路径结构的3D-DPN-50、只加入时空多尺度特征融合层的3D-Res2Net-50,以及同时加入两种改进结构的3D-MsDPN-50进行比较。4种网络第1层卷积均为64个的(7×7×7)卷积核，之后有4个时空卷积块。每个卷积块前均有时空池化层，采用平均和最大两种池化方式，第1层池化窗口为(3×3×3)、步长为(2,2,2)，其余各层池化窗口均为(2×2×2)。在第4个卷积块后进行全局池化，使用以log softmax为激活函数的全连接层作为分类器。各网络卷积块内的具体结构如表1所示，表中括号内数字为每层卷积核数量，G=x为分组卷积的分组数，(+x)表示密集连接路径的特征增长数。

表1 不同3D卷积网络各卷积块结构对比

表2对4种网络对应的参数量、计算复杂度及实验数据集分类准确率进行了对比。可以看到3D-DPN结构由于同时具有残差和密集连接，其参数量和计算复杂度相比于基准模型小幅提升。3D-Res2Net结构由于其时空多尺度特征融合层第一组特征图不进行卷积，相比于基准模型减少了参数量及计算复杂度。双路径结构及时空多尺度特征融合层的加入均可以提升网络的分类准确率，两者共同作用下，3D-MsDPN相比基准模型在参数量及计算复杂度分别增加3.19%和 1.49%的前提下，在UTD-MHAD和IsoGD两个数据集以深度视频为输入的测试集分类准确率分别提升了1.86%和3.76%。

表2 不同3D网络参数量、计算复杂度及实验数据集分类准确率

图7显示了4种网络结构在IsoGD数据集训练过程中测试样本损失函数的收敛过程。可以看到双路径结构和时空多尺度特征融合层的加入并没对网络收敛速度造成影响，Res2Net和MsDPN由于加入多尺度特征融合层在训练过程中收敛更加稳定。

为进一步分析多尺度特征融合层的作用，将DPN和MsDPN网络卷积块1的第3个卷积单元的中间层输出进行比较，该层输出时空特征图的时间步长为8，抽取中间4个时间步的输出结果，将所有特征通道相加后进行显示，结果如图8所示。展示样本为UTD-MHAD数据集中编号为12的抛保龄球动作，其中图8(b)中每行依次为多尺度融合层4个分组的输出。可以看到不含多尺度层的DPN网络输出特征图主要在脚部和右臂区域激活且激活区域尺寸固定，范围相对较小。加入多尺度融合层后网络在双脚、头部和手臂区域都有较大激活，且不同分组的激活范围存在明显差异，这说明多尺度融合层为后面卷积层提供了更丰富的特征选择空间。

网络深度、宽度和多尺度融合层的分组数目对网络性能的影响如表3所示。

表3 网络规模对参数量及分类准确率的影响

表3中38层网络各卷积块卷积单元数依次为3、3、3、3，101层依次为3、4、23、3。将表1展示的MsDPN结构宽度记为W，每层卷积核数量减半的网络宽度记为0.5W，翻倍的为2W。通过表3的对比结果可以看到，随着网络深度和宽度的提升，在IsoGD数据集深度视频测试样本的分类准确率也在提升，当网络深度达到50层、宽度达到W时分类准确率接近饱和。对多尺度特征融合层分组数进行分析，当分组数为1时网络退化为3D-DPN结构，参数量最大。当分组数为2时只有一半特征通道进行卷积运算，参数量下降但分类性能也随之下降。当分组数为8时多尺度结构过于冗余难于训练，分类准确率同样出现下降。综合来看，选择50层卷积、宽度为W、多尺度融合层分组数为4的网络可以达到参数量和分类准确率的平衡。

3.6 特征融合算法比较

用灰度、光流和深度3种输入模态分别训练3D-MsDPN-50网络，将网络全局池化层输出作为特征层融合输入特征、网络最后的全连接层输出作为决策层融合输入特征。将DMCCA方法与其他特征融合方法进行比较，结果如表4所示。

表4 不同特征融合方法分类准确率对比

表4中特征层融合时的DCCA和DMCCA方法均采用3层全连接神经网络，3层神经元数量依次为2560、2560、1024，均采用sigmoid为激活函数。在决策层进行如图6所示的DMCCA融合时，IsoGD数据集其对应的3层全连接网络的神经元个数分别为1024、512、249，参数量为1.42×106，单样本FLOPs为2.83×106，UTD-MHAD数据集对应的DMCCA网络3层神经元个数分别为128、64、27，其计算复杂度相较于时空卷积网络基本可以忽略不计。从表4可以看到，在不使用典型相关分析的特征融合方法中，在特征层进行拼接融合并使用线性SVM作为分类器的效果最好。在特征层和决策层进行DMCCA融合的效果好于CCA、DCCA方法及其他融合算法。在特征层通过加权的DMCCA相比于未加权的DMCCA在两个数据集上的分类准确率分别提升了0.73%和0.47%，在决策层分别提升了0.49%和0.47%，这证明了在总相关系数中进行加权可以起到提升分类准确率的作用。最终使用线性加权的DMCCA进行决策层融合在两个数据集上分类准确率达到了72.65%和98.14%。

3.7 与现有方法的对比

将本文方法在UTD-MHAD和IsoGD两个数据集上与基于其他模型的研究结果进行了对比，结果如表5和表6所示。本文方法在UTD-MHAD数据集上相比于此前最好的研究结果[16]将测试集分类准确率提升了3.86%，在IsoGD数据集上相比于此前最好的研究结果[19]将测试集分类准确率提升了4.51%。分类准确率的提升是时空网络结构改进、新的视频数据增强方式以及新的特征融合算法3个方面因素共同作用的结果，其中网络结构改进和特征融合的作用更为显著。

表5 在UTD-MHAD数据集上与其他研究的对比

表6 在IsoGD数据集上与其他研究的对比

4 结束语

本文提出了一种新的3D卷积网络结构3D-MsDPN并将其用于行为识别。该网络通过双路径结构提升了特征提取能力，通过时空多尺度特征融合层提升了对不同时空尺度特征的表达能力。设计了一种新的深度多特征典型相关分析网络用于灰度、光流和深度输入的决策层多特征融合。本文方法在UTD-MHAD和IsoGD两个公开行为识别数据集上的分类准确率分别达到了98.14%和72.65%，高于现有其他研究。将该网络结构与循环网络结合用于长时间复合行为识别是下一步的工作重点。