基于中点弦测法的中低速磁浮轨道不平顺检测

高雄杰，于 龙，陈唐龙

(西南交通大学 电气工程学院，四川 成都 610031)

现有的轨道不平顺检测方法主要可分为弦测法和惯性基准法两大类。目前国内关于磁浮轨道不平顺检测系统的研究主要针对上海的高速磁浮轨道交通系统，检测系统安装在磁浮列车上，采用惯性法检测磁浮轨道不平顺[1-3]。惯性基准法对传感器要求较高，主要应用在高速检测条件下。为长沙中低速磁浮线路研发的综合检测车运行速度不超过30 km/h，而弦测法不受检测速度的影响，故更适合采用此种检测方式。文献[4-8]介绍了弦测法的相关理论及特性研究，文献[9]使用1D激光位移传感器检测轨道高低不平顺，对1 m的标准钢轨进行了试验，检测数据采用FIR逆滤波进行数据复原。文献[10]采用点位计式位移传感器设计手推式波磨检测小车，文献[11]设计了单轨轨道的线形检测系统，并对弦测法测量的数据进行了统计方面的分析。可以看出以上文献都是传统的轨道检测应用，而中低速磁浮有不同的运行环境及不同的F轨轨道特征。目前尚无将弦测法用于磁浮轨道不平顺动态检测的研究。本文研制了车载非接触式中低速磁浮F轨动态检测装置，采用线结构光传感器，获取F轨轨道轮廓信息的二维图像，基于机器视觉技术将三点弦测法运用于中低速磁浮轨道不平顺检测中，通过三个共线标定过的激光摄像式传感器采集F轨轮廓图像，提取出F轨外磁极面轨距点，得到轨距点距离信息，算出轨道不平顺正矢值，并由“以小推大”公式得到不同弦长的不平顺。

1 F轨轨道不平顺

图1(a)为F轨轨道截面，F轨因形似字母F而得名，轨道在轨枕两侧铺设开来，主体部分悬空。

图1(b)为F轨道效果图，上表面是一层直流电机反应板，下凹槽面是磁浮间隙检测面，底部表面为内、外磁极面，外磁极面与侧面的交点为F轨轨距点。

图1 磁浮轨道示意图

轨道轨向(高低)不平顺为钢轨在左右方向(高低)与钢轨理想位置几何尺寸的偏差，表征钢轨水平(竖直)方向上的弯曲程度。三点弦测法可测轨道轨向不平顺，见图2，将两个轨道简化为圆弧，过线段AB上的点C做垂线交圆弧于点D，CD长度Vi即为轨向不平顺值。若C点为AB的中点，则称为中点弦测法(正矢法)，对应的Vi称为正矢值。高低不平顺同理。本文讨论固定弦测的不平顺。

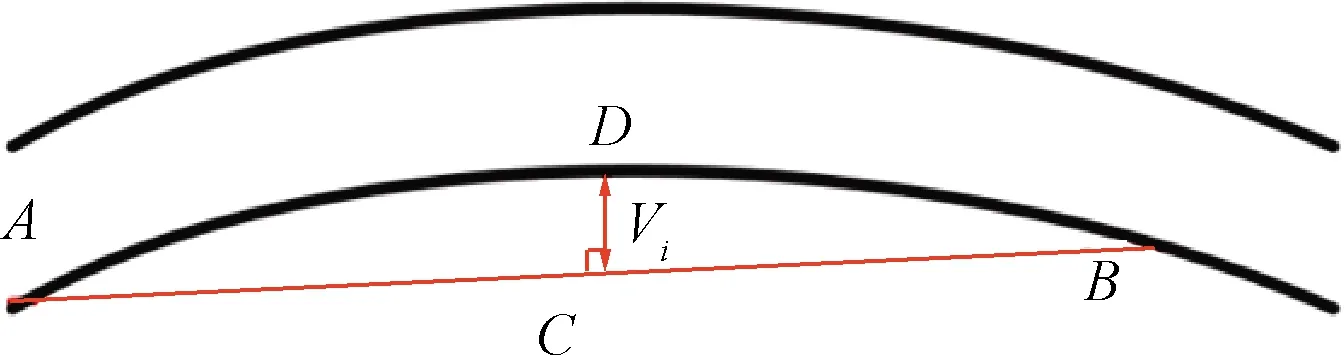
图2 弦测法测轨道不平顺

2 基于机器视觉的三点弦测法

2.1 检测原理

磁浮轨道不平顺检测主要采用激光摄像式传感器，激光摄像式传感器由激光器和工业相机组成，激光器发出的线结构光面与相机图像具有对应关系，对应关系的查找过程称为标定，常用的标定方式有棋盘格标定法、针型靶标标定法等。

传感器的布置图见图3(a)，左右轨道分别使用一组激光摄像式传感器，三个传感器为一个弦测组，传感器中心轴线分别对应F轨轨距点，激光光面垂直于轨道走行方向，相机拍摄范围覆盖F轨侧面和磁极面。左右弦测组的排布见图3(b)；左右侧弦测组激光打到F轨轨道上的示意见图3(c)，在外磁极面上有一道激光线，外端点处为F轨轨距点。

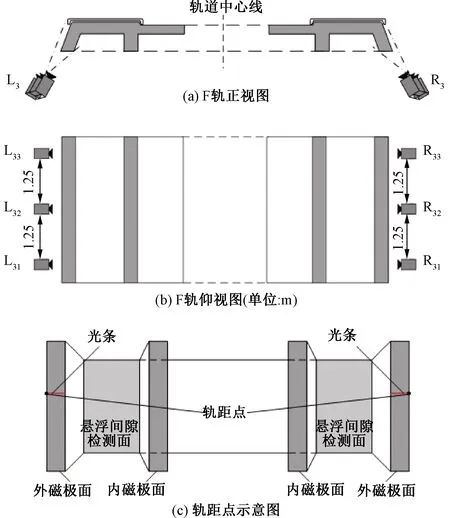
图3 F轨轨道不平顺检测传感器位置图

检测流程如下：

(1)检测车运行过程中，带动安装在车轴上的速度传感器脉冲计数，可根据车轮轮长记录车体行走距离，并触发左右侧弦测组传感器采集图像。

(2)对同一组F轨轨廓激光光条图像进行裁剪、光条提取、轨距特征点图像坐标提取。

(3)将轨距特征点图像坐标，通过摄像机内外部参数建立的视觉测量模型对应关系，得到在世界坐标系下的特征点坐标，即可计算相关的方位距离信息。

(4)将实时的特征点坐标，通过对比静态条件下已标定的特征点基准，计算得到正矢值，并通过“以小推大”等方式得到不同弦长的不平顺值。

在某时刻下，传感器检测F轨轨道不平顺示意见图4。

( 1 )

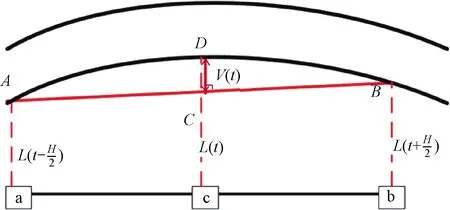
图4 弦测法测轨道不平顺

式中：H为弦长；L(t)为某时刻下轨道与传感器的距离。对式( 1 )进行傅里叶变换可得传递函数为

N(ω)=1-cos(πH/λ)

( 2 )

式中：ω=2π/λ为空间域角频率；λ为轨道不平顺波长。根据式( 2 )可知，幅值增益与速度无关，由此可得各条件下的增益情况，如表1所示。

表1 弦测法的传递函数幅值

针对弦测法的限制，可采取“以小推大”、插值和滤波算法等进行改进。通过车载检测设备，可在动态条件下对F轨轨道不平顺进行连续测量。

2.2 F轨轨距点的提取

通过对全线拍摄到的F轨光条波动范围进行统计，对图像有效ROI进行裁剪，利用灰度重心法提取F轨光条中心曲线，并进行滤波得到光条中心坐标(x1,y1)，(x2,y2)，(x3,y3)，…，(xn,yn)，…。图5为激光打在F轨轨道上的拍摄图，光条拐点即为F轨轨距点。由于单点受干扰波动性影响较大，故采取最小二乘法拟合直线的方式选点。

(1)先遍历整组坐标，找到纵轴极值点yi，将A(xi,yi)选定为轨距点坐标初值。

(2)以A点为中心，向数组两边遍历，距初值各取一定长度点集，采用最小二乘法拟合出直线。

(3)计算两条直线的交点，即为最终的轨距特征点。

将弦测组采集到的轨距特征点记为A1k(x1i,y1i)、A2k(x2i,y2i)、A3k(x3i,y3i)，k为采集的次数。

图5 F轨激光轮廓图像

2.3 正矢值的检测

由于弦测组三个相机在实际拍摄过程中的角度存在略微不同，且各自对应的世界坐标系不共线，因此要进行共线标定，归一化处理。

(1)调整三个相机的坐标系基准

对于弦测组相机拍摄角度略微偏差的问题，需选取共同的坐标平面进行统一。图6为相机拍摄F轨坐标系示意图，可将标准外磁极面FH作为基准，通过式( 3 )转正坐标系。右侧同理。

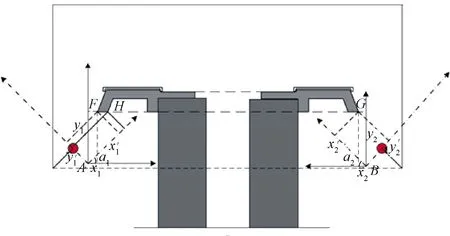
图6 F轨及传感器模拟图

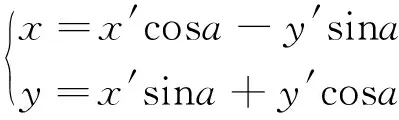
( 3 )

(2)三个相机共线标定

弦测组坐标系转正后坐标系原点为A1、A2、A3，见图7(a)，以点A2为基准，计算A1和A3偏移量，将坐标系归算到T2坐标系，得到如下公式

( 4 )

( 5 )

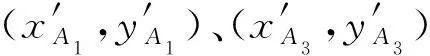
( 6 )

式中：Vi、Ui为轨向、高低不平顺正矢值。

弦测组坐标系的间距Z1、Z2即为各激光光面的纵向距离，见图7(b)。

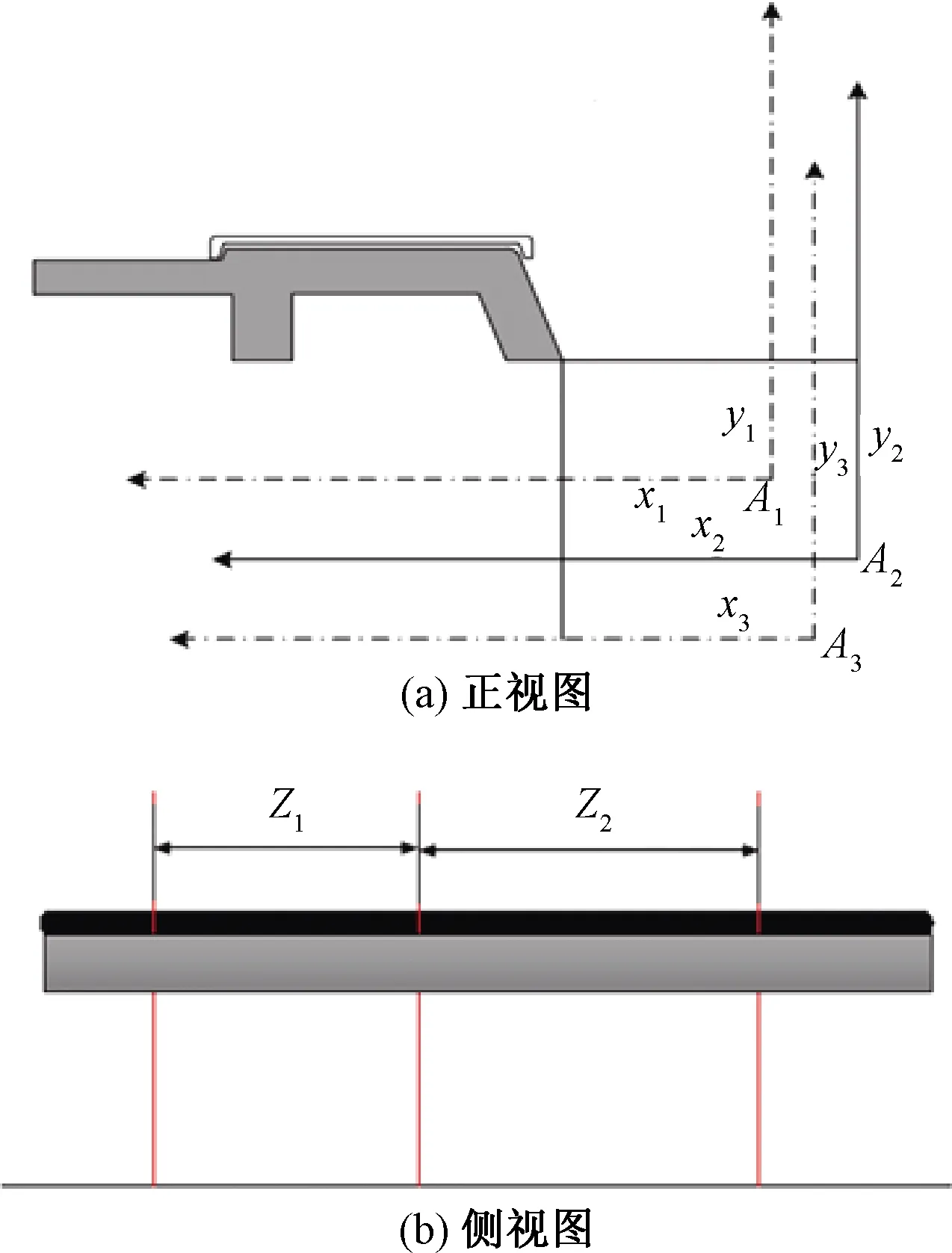
图7 三个相机坐标系模拟图

2.4 不平顺数据拟合

由固定弦长的正矢值，可通过“以小推大”[10]、插值和滤波算法得到其他固定弦长的轨道不平顺。如图8所示，在一个圆弧上，1，2，3，…，2n-1为圆弧的等分点，以弦长H连接两等分点作图。得到V1为第一个弦测值，V2为第二个弦测值，…。通过中点弦测量值V1，V2，…，Vn，Vn+1，…，V2n-1可求得弦长AB的中点弦测值VL，其中n=|AB|/H。

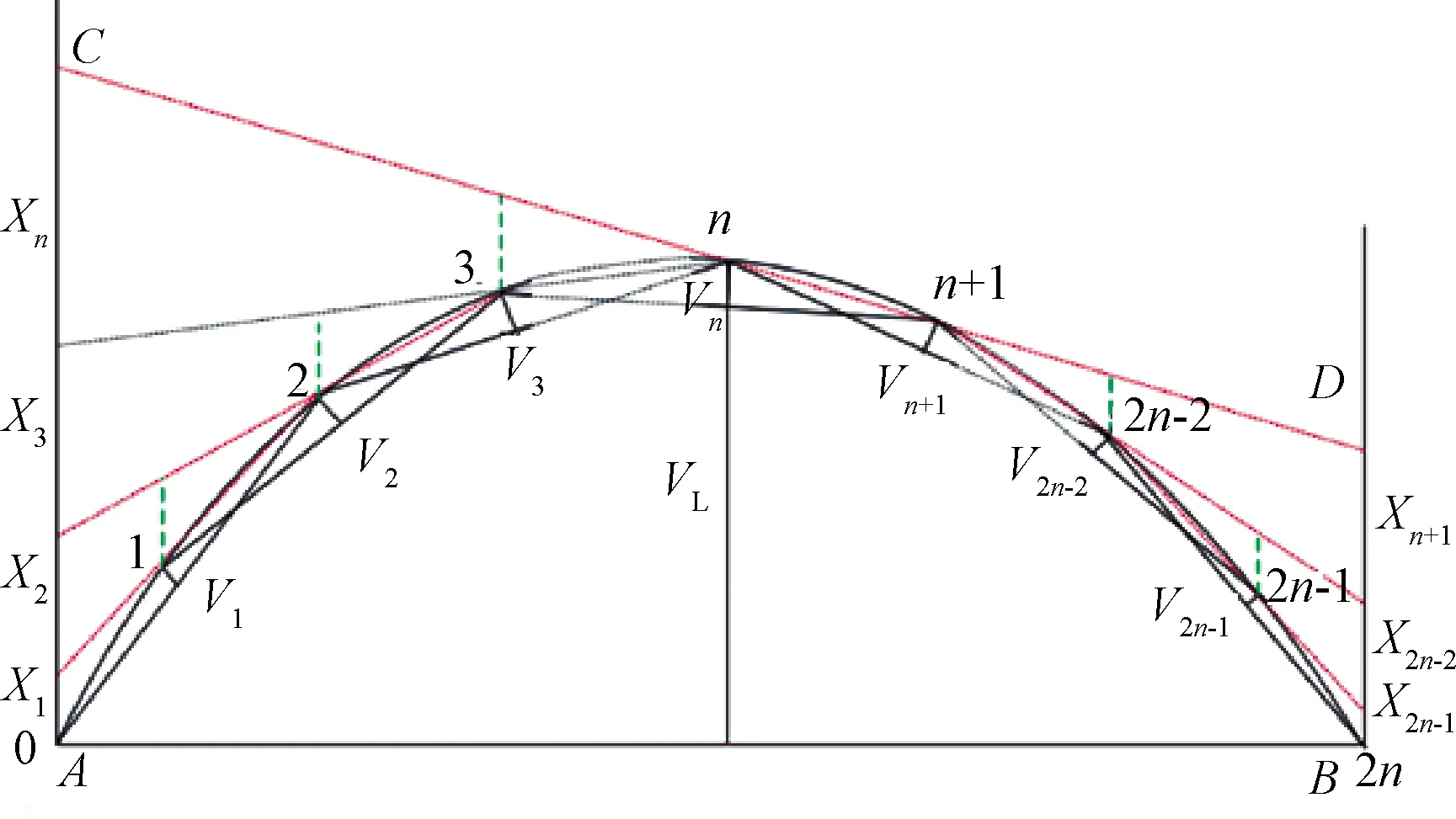
图8 基于中点弦测法的矢距计算通式示意图

AC、BD与VL平行，而|AB|取值数米及以上，VL取值在毫米级别，所以|AB|通常远大于VL，那么可近似认为V1,V2,…与线段AC、BD平行。

VL=(|AC|+|BD|)/2

( 7 )

Xn=(2·Xn)·n

( 8 )

则

( 9 )

|BD|≈2V2n-1+2(2V2n-2)+…+(n-1)(2Vn+1)=

(10)

所以

(11)

由此推导，弦长为H，步长为H/(2m)(m为正整数)时，长度为i·H/2(i为正整数)的弦测值公式

(12)

式中：n=(i·H/2)/H=i/2,即已知弦长H的正矢值时，可推导长度为H/2整数倍的不平顺值。对于其他弦长的不平顺值，通过Newton插值法[4]近似得到。

本文检测装置组成2.5 m弦长，设备检测步长为0.25 m，可计算得到4、10 m弦测值公式为

(13)

(14)

3 试验

3.1 F轨轨道不平顺测量方法验证

为了验证该方法的有效性及检测设备的稳定性，进行动态重复性对比试验：在相同运行环境下，检测车匀速、同方向、多次测量相同路段，通过对比检测结果验证检测装置的稳定性。检测结果满足重复性95%最大偏差值的精度要求，则判断系统重复性合格。根据相关部门对中低速磁浮轨道检测设备的精度要求，轨道不平顺4 m和10 m弦的检测精度要在0.5 mm和1.5 mm内。其中95%最大偏差值指的是对比数据之间的差值按从小到大顺序排列，排在数据总数95%位的数据。

3.2 试验环境

选择株洲电力机车有限公司的磁浮交通系统中心试验线为试验地点(图9)，轨道检测车见图10，检测设备主要由图像采集模块、综合定位模块、数据处理模块以及电源控制模块组成。车上安装有两个机柜，主要放置数据处理模块、电源控制模块。在车体两侧均设置了前、中、后端三个测量架，用于安装图像采集设备，激光摄像式传感器为采集单元，按照1.25 m间隔安装，三个传感器组成弦长为2.5 m中点弦测模块，激光摄像式传感器的标定可参考文献[12]。

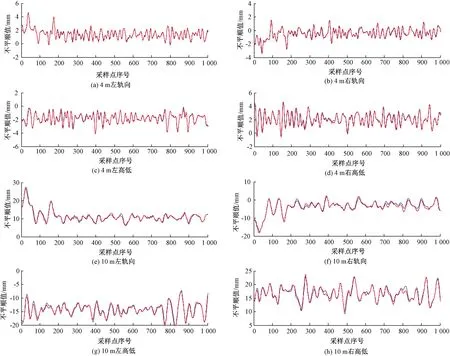
图11 同速度下不平顺数据对比

图9 磁浮交通系统中心试验线

图10 F轨轨道不平顺检测车

3.3 同速度下重复性试验

选取磁浮试验线路中的一段，检测车以20 km/h的速度进行两次检测，软件每0.25 m输出4 m和10 m弦测高低、轨向不平顺值。截取1 000个值进行对比，见图11。蓝色与红色曲线为两次相同起点的检测结果，其中正负值代表实际轨道弯曲的两个方向。

将两次检测数据进行对比分析，统计结果如表2所示，可得F轨4 m弦测轨向/高低不平顺值的重复性95%最大偏差值为0.301/0.441 mm，10 m弦测轨向/高低不平顺值的重复性95%最大偏差值为1.425/1.348 mm，满足设计要求。

3.4 不同速度下重复性试验

选取磁浮试验线路中的一段并记录起始位置，检测车分别以20 km/h和25 km/h的速度进行两次检测，软件每0.25 m输出4 m和10 m弦测高低、轨向不平顺正矢值。截取1 000个值进行对比，见图12。

将两次检测数据进行对比分析，统计结果如表3所示，可得F轨4 m弦测轨向/高低不平顺的重复性95%最大偏差值分别为0.417/0.451 mm，10 m弦测轨向/高低不平顺的重复性95%最大偏差值分别为1.420/1.451 mm，满足设计要求。

表2 相同速度下的不平顺重复性偏差统计

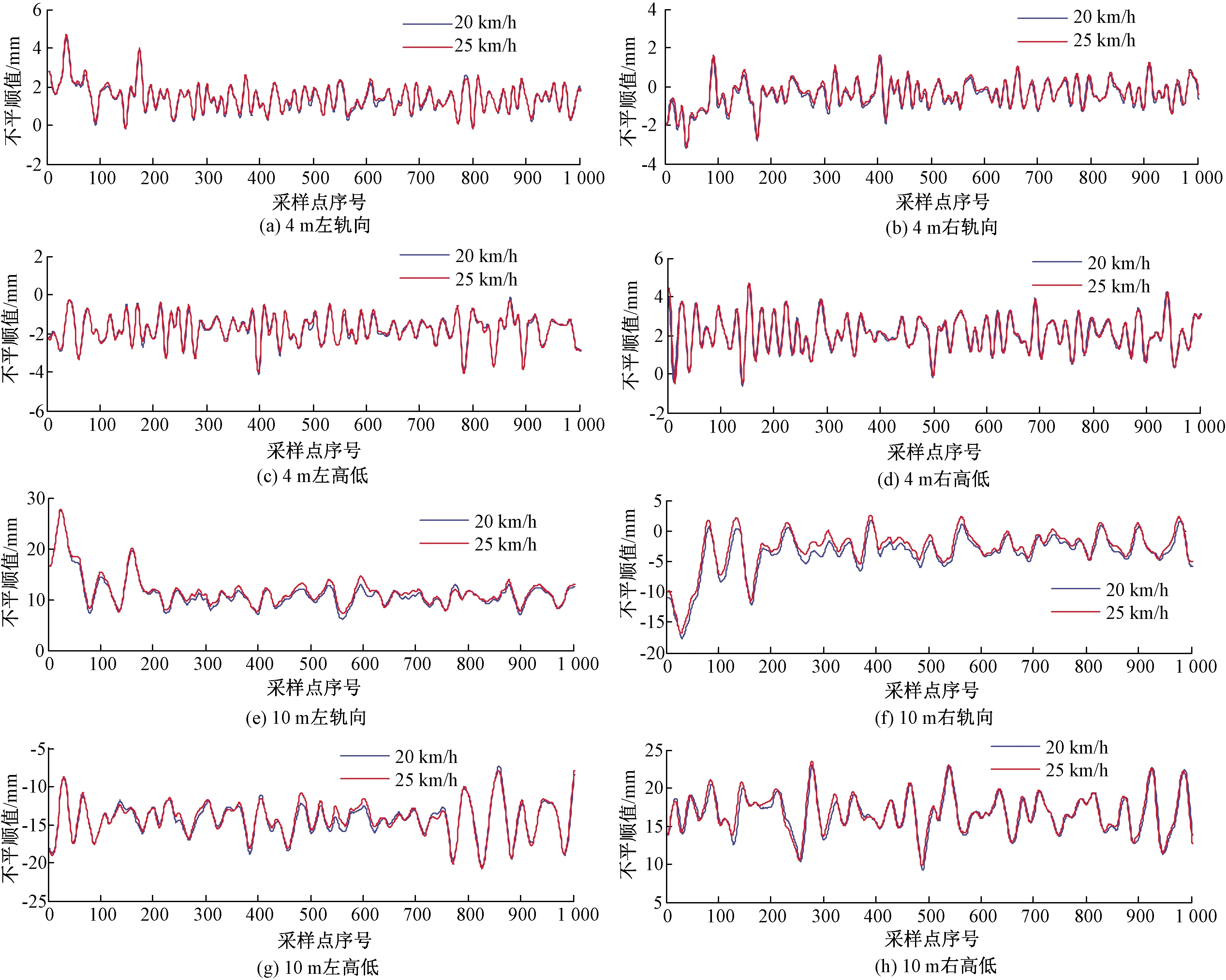
图12 不同速度下不平顺数据图

表3 不同速度下的不平顺重复性偏差统计

4 结论

本文基于激光摄像测距技术，建立三个视觉传感器的全局测量模型，采用三点弦测法计算F轨轨道正矢值，利用以小推大方法拟合轨道不平顺。给出了基于中点弦测法的中低速磁浮F轨轨道不平顺测量方案。研制了中低速磁浮F轨轨道不平顺检测装置，对该装置在实际线路中进行动态测量试验。试验表明，在20 km/h同速度下和20、25 km/h不同速度下测量的4 m(10 m)弦水平、高低不平顺重复性偏差95%最大偏差值均在磁浮轨道检测标准要求的精度0.5 mm(1.5 mm)范围内,验证了该方法切实可行。