考虑解编调车成本的铁路技术站调车线运用优化
赵 军,张思宇,彭其渊
(1. 西南交通大学 交通运输与物流学院,四川 成都 611756;2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 611756)
调车场是铁路技术站里的重要调车设施,是供中转车、本站作业车、维修车等车辆集结和停留的场所。车辆/车流去向-调车线的指派方案不仅直接影响驼峰解体和峰尾编组调车工作的质量,也限制车流推算、调机运用等车站作业计划的可行性。目前,我国大多数技术站里,主要采用固用活用相结合的经验规则使用调车线,此做法固然可降低调车线运用计划的编制难度,但不适用于车流去向多、车流波动性强的技术站,也不利于控制解编调车成本及发挥调车场的能力。根据各类型车辆对调车场的占用需求,并结合调车线的固定使用方案,研究调车线灵活运用的优化方法,是技术站作业计划编制需解决的重要问题。
目前国外针对技术站调车线运用的研究不多。国外技术站调车作业压力一般较小,列车解体和编组都由驼峰来完成,各去向的车辆可溜放到不同的调车线上,若调车线数量不足,某些去向的车辆需暂时停放在“混合线”上,后续再拉回驼峰进行二次解体,直到所有出发列车按要求完成编组。对此,Bohlin等[1]研究了含混合线的列车-调车线指派问题,以总重复解体车数最少为目标,分别建立了基于生成列和弧索引的整数规划模型,并提出分支定价和滚动时域算法。Gestrelius等[2]进一步将出发列车的站顺要求纳入列车-调车线指派,构建了基于生成列的整数规划模型,并采用分支定价算法求解。此外,国外还探讨了含调车线指派的作业计划综合编制问题。例如,Gestrelius等[3]研究了列车-到达线/调车线指派与解体/编组排序综合问题,提出了最小化重复解体车数和线路占用成本的整数规划模型。Haahr等[4]针对车流推算、解体/编组排序和调车线指派综合问题,设计了分解算法,其中,构建解体排序和编组排序问题的整数规划模型,调车线指派由贪婪启发式规则求解。Raut等[5]研究了相同的问题,但提出了整个问题的混合整数线性规划模型,并采用滚动时域算法求解。
国内对技术站调车线运用开展了一定工作。在我国技术站特别是编组站,每天的改编工作量大,应用国外的解编调车模式会导致大量的重复解体工作,影响调车场的使用效率,由此,现场通常规定驼峰主要负责解体,而峰尾主要负责编组作业。根据国内实际情况,早期,任勇[6]、孙玉明等[7]和陈伯羽[8]主要探讨了制定调车线固定使用方案的量化方法。近来,国内更关注技术站作业计划编制阶段的调车线灵活运用方法。薛锋等[9]以出发列车集结占用线路数、调车线集结车流去向的分散度和调车线的空闲车数为目标,建立调车线调整运用优化模型。黎浩东等[10]构建了最小化“整理线”数量和出发列车连挂次数的调车线运用优化模型。张英群等[11]在此基础上设计了禁忌算法求解模型。Zhang等[12]进一步考虑站顺编组要求,对调车线运用模型进行拓展,并开发禁忌搜索算法求解。马亮等[13]引入固定属性作为车组的特征,以此为基础,建立以调车线混乱度最小和占用优先级最大的优化模型,并设计启发式回溯算法。
综上,技术站调车线运用尚未引起国内外广泛关注,国外方法不适用于我国实际情况,国内针对调车线固用和活用做了许多尝试,但还存在进一步研究的空间,在编制作业计划时,需根据车辆和调车场的实际情况,快速生成解编调车成本更低,满足作业计划兑现需要的调车线灵活运用方案。文献[10-12]对本文工作有所启发,但存在一些可改进的地方。文中提出了整理线这一概念,并尝试最小化其数量,但没有提出在这类线路存在时如何处理,事实上,整理线一旦出现,会给技术站带来额外调车负荷,在制定调车线运用计划时,应尽可能避免存在整理线。此外,仅使用出发列车连挂次数描述调车成本,不能具体刻画由调车线运用产生的解编调车成本,还可能导致最优解集过大,影响模型算法求解性能。
本文研究技术站作业计划编制阶段的调车线灵活运用优化方法。定义由调车线运用带来的解体和编组调车成本,并根据固定使用方案引入车组-调车线占用权重。以总加权解编调车成本最小为目标,考虑车组溜放和连挂、出发列车编组顺序和调车线能力等要求,构建0-1非线性规划模型,基于图的极大团提出溜放和能力约束的紧凑表达式,该模型容易简化为线性模型,并由商业软件直接求解。最后采用算例验证所建模型。
1 问题描述与假设
1.1 问题描述
本文考虑技术站的1个调车场在给定计划时段内的调车线运用问题。典型调车场的结构见图1,该车场一端与到达场相邻,两车场一般以调车信号机分界(例如D201),中间设有驼峰,是到达列车解体的场所;另一端连接出发场,两车场也以调车信号机分界(例如D301),中部是峰尾,出发列车往往在这里编组。调车场由若干条平行且长度不一的线路组成,根据车站布置结构的不同,每条调车线可通达所有的或者部分驼峰溜放线和峰尾牵出线。对于各调车线,从与到达场分界的调车信号机至该条线入口端调车表示器的线路称为溜放进路,从该条线出口端调车/发车信号机至与出发场分界的调车信号机的线路称为连挂进路,该条线入口端调车表示器与出口端调车/发车信号机间的线路是可供车组集结的场所。

图1 调车场示意图
计划时段内:A为到达列车集合;D为出发列车集合;R为调车线集合。到达列车有|A|列,各到达列车由若干去向的车辆组成,其编组内容、编组顺序、解体起时和终时已知,将计划时段初调车场的现在车视为1列虚拟到达列车。出发列车有|D|列,各出发列车的编组内容由提前确定的车流推算方案给定,其编组起时、终时已知,且必须按照给定的车流去向排列顺序要求完成编组。根据车流推算结果,将计划时段末各去向的残存车分别视为1列虚拟出发列车。根据到达列车信息和车流推算方案,将到达列车中的车辆划分为若干车组,作为调车线指派的基本对象,其集合为C。车组共有|C|个,各车组中的车辆来自于同一到达列车、具有相同的去向且紧邻编组、并将接续同一出发列车,规定各车组在解体时需以一钩溜往同一条调车线,且在编组时在其集结调车线上以一钩完整连挂牵出。
共有|R|条调车线可用于车组集结占用,其能力以其有效长度量。规定各车组在其对应到达列车解体开始时即预定/实际占用为其指派的调车线,并在其接续的出发列车编组结束时才释放对其指派调车线的占用。已知去向-调车线固定使用方案,各调车线可集结其固定和非固定去向的车组。各出发列车的车组可在多条调车线上集结,由多次连挂完成编组,各次连挂需将对应调车线上属于该出发列车的车组全部牵出。为降低峰尾编组调车工作负担,要求在各调车线上,任意车组的编组开始时刻不能早于比其更靠近峰尾车组的编组结束时刻,若如此,必然需在峰尾进行必要的中部挑车调车作业,增加额外编组作业时间。同时,各调车线的容车能力是有限的,任意时刻集结的车组总长不能超过其有效长。
接下来分析调车线运用对解编调车成本的影响。从图1可见,车组经驼峰解体调车从到达场进入调车场,再经峰尾编组调车离开调车场进入出发场,为该车组指派哪条调车线主要影响其解体调车时的溜放作业过程和调车线上的走行过程、及峰尾编组时的连挂作业过程。因此,在研究的调车场范围内,将各车组视为质点,将其解编调车过程划分为溜放走行和连挂走行两部分。
r为调车线,r∈R;hr、lr和pr分别为调车线r的溜放进路长度、有效长和连挂进路长度,m。规定各车组的解体调车成本与其溜放走行距离正相关,后者取为该车组指派调车线r对应的hr与lr之和。各车组的编组调车成本与其连挂走行距离正相关,后者的度量相对复杂,同时与为该车组指派的调车线r以及该车组接续出发列车的连挂作业有关。
例如,对车组连挂走行距离的度量进行描述。已知有1列出发列车,含5个车组(C1~C5),车组C1和C2在调车线R1集结,车组C3~C5在调车线R2集结,根据编组顺序要求,需依次对调车线R1和R2进行连挂。该出发列车的完整连挂过程见图2。

图2 连挂走行距离的度量
由图2可知,若将各车组视为1个质点,对于车组C1和C2,在第1次连挂中,其连挂走行距离为p1,在第2次连挂中,该两车组需要首先跟随调机前往调车线R2连挂车组C3~C5,走行p2,之后再随调机返回牵出线,再次走行p2。车组C3~C5在第1次连挂中无需走行,第2次连挂中的走行距离为p2。因此,车组C1和C2在连挂过程中需要走行的距离为p1+2p2,车组C3~C5在连挂过程中需要走行的距离为p2。
稍加整理,可得出一般性规律。若出发列车d的车组分布在|K|条调车线上,则在其编组过程中需进行|K|次连挂,一般的,各出发列车只进行有限次连挂,可根据实际情况确定一个|K|的取值上限。若其中一个车组c于第k次被连挂牵出,在编组出发列车d进行第k′(k≤k′≤|K|)次连挂时,都会产生一段连挂走行。当k′=k时,车组c的走行距离为发生第k′次连挂所在调车线对应的连挂进路长度;当k′>k时,车组c的走行距离为发生第k′次连挂所在调车线对应的连挂进路长度的2倍(随调机往返于第k′次连挂的调车线)。
注意,本文对车组在进出调车线上的走行距离的度量做了适当简化,但相比于既有研究[9-13],可更为细致地刻画因调车线运用带来的解编调车成本,并在一定程度上降低模型的建模难度和求解难度。
综上,技术站调车线运用问题可描述为:给定计划时段内的车流推算方案(到发列车的车流接续方案)、到达列车的解体方案(解体起时、终时)、出发列车的编组方案(编组起时、终时),以及车流去向-调车线固定使用方案,为各车组指派调车线,以使得调车线占用不冲突、出发列车编组顺序要求和调车线能力限制等约束得到满足,且综合衡量解编调车成本和调车线固定使用方案的总加权解编调车成本达到最小。
1.2 问题假设
根据给定计划时段内提前确定的车流推算方案和列车解编方案,重在为到发列车间接续的有调中转车辆指派调车线。为便于后续方法阐述,提出以下假设:
(1)不使用本站作业车、检修车、禁溜车、特种车等车辆固定占用的调车线。
(2)只考虑受调车线运用影响的解编调车成本,包括解体调车过程中的溜放成本和编组调车过程中的连挂成本。
(3)不考虑列车/车辆的解体溜放和编组连挂的具体调车作业过程。
2 数学模型
2.1 符号定义
文中主要集合、参数和变量定义见表1。

表1 集合、参数及变量定义
2.2 目标函数
调车场是技术站的调车设施,衡量调车线运用方案优劣的标准可为调车成本。受调车线运用影响的调车成本主要是解体溜放成本和编组连挂成本,1.1节对各车组的溜放成本和连挂成本的度量进行了说明。同时,为简化调车工作,现场倾向于尽量按固定使用方案为车组指派调车线。因此,引入车组-调车线占用权重,提出总加权解编调车成本最小的目标函数,以期得到不仅调车成本低而且容易被现场接受的调车线运用方案,目标函数为
(1)

为尽量照顾调车线的固定使用方案,wcr的取值规定为:若调车线r是车组c的固用线路,即r∈Fc,取wcr=1;否则,将wcr设置为调车线r离车组c的所有固用线路的最小线间距,即wcr=min{grr′,r′∈Fc}。根据现场情况,不同调车线的总溜放和连挂走行距离的比值一般不超过1.5,且相邻调车线的线间距一般不小于5 m。显然,wcr的取值可使得各车组尽量在其固用调车线里选择解编调车成本小的线路,若能力不足,也优先选择离其固用线路近且调车成本小的调车线。wcr的不同取值对计算结果的影响在3.2.4节作对比分析。
2.3 约束条件
2.3.1 唯一性约束
各车组经解体溜放作业从驼峰进入调车场,再由编组连挂作业由调车场进入峰尾牵出线。由此,在溜放过程中,车组c必须且仅能溜放到某条调车线r上,即
(2)
在连挂过程中,各车组c必须且只能在其归属出发列车的某次连挂k时于某条调车线r上牵出,即
(3)
各出发列车d在进行编组作业时可能经过一次或多次连挂才能编成,规定各次连挂k(如果存在)必须发生在某条调车线r上,且在各条调车线r上最多进行一次连挂,即各出发列车d的各次连挂k需将对应调车线r上集结的且属于该出发列车的所有车组牵出,即
(4)
(5)
各出发列车d必然至少需要进行一次连挂,即
(6)
此外,变量xcr、yckr和zdkr需满足关系约束
yckr=xcr·zdkr∀d∈D,c∈Cd,k∈K,r∈R
(7)
式(7)表示只有当出发列车d的第k次连挂在调车线r上执行(zdkr=1),且其包含车组c也正在调车线r上集结(xcr=1)时,车组c才会在其归属出发列车d的第k次连挂时从调车线r上牵出(yckr=1)。通过式(7)可正确控制3个决策变量的取值。
2.3.2 溜放约束
为减轻峰尾编组调车工作压力,具备以下冲突的车组不能溜往同一条调车线。
(1)编组时段冲突
属于不同出发列车的车组在编组时段上可能存在冲突,简称编组时段冲突(Conflict of Assembly Interval, CoAI),不能在同一条调车线上集结。具体地,对于任意两属于不同出发列车的车组c和c′,假设车组c的解体开始时刻比c′的早(ec
参照文献[10-12]的建模方法,可对所有车组C按解体开始时刻ec从小到大排序,然后对两两具有CoAI冲突的车组建立约束
vc-uc′≤M(2-xcr-xc′r)
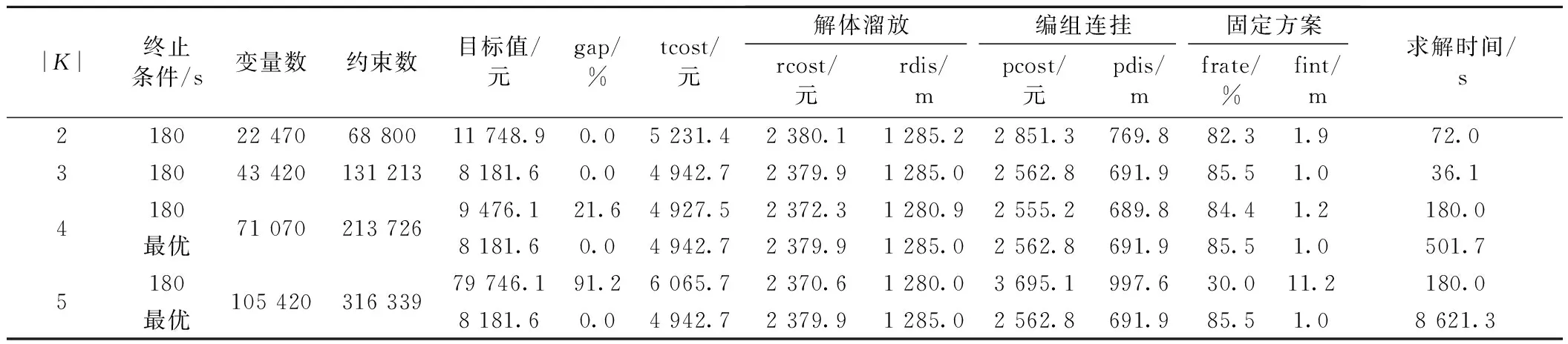
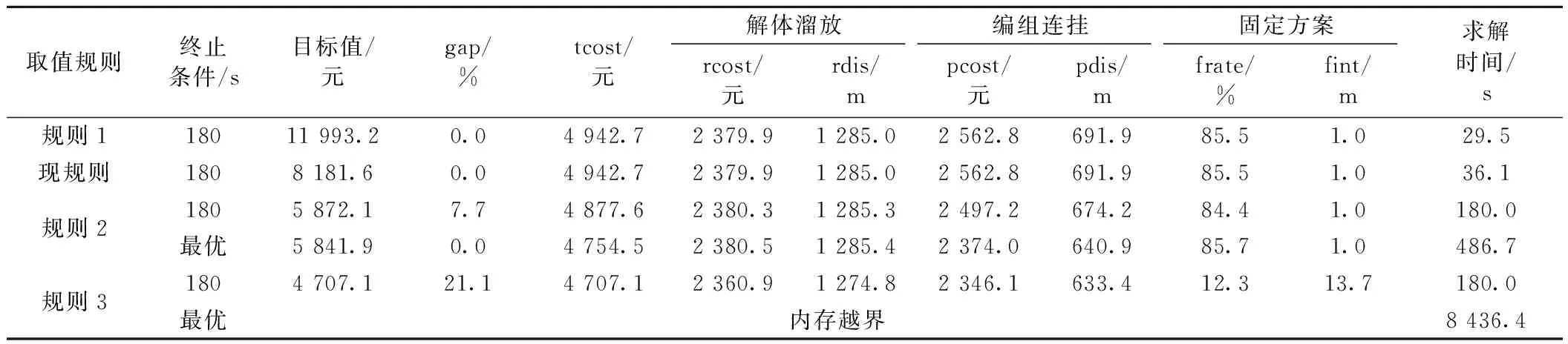
∀c,c′∈C|c (8) 式中:M为充分大正数。 式(8)可确保具备CoAI冲突的车组不占用同一条调车线,但这类方法只针对两两车组引入约束,使得各约束只含2个变量,可能导致整个优化模型的线性松弛结构松弛,影响求解性能。这里,利用图的极大团对这类约束进行改进。 引入无向冲突图G1=(C,I1),其中,顶点集C为车组集,边集I1表示车组的CoAI冲突,若车组c和c′具有CoAI冲突,则在这两车组对应的顶点间连1条无向边。车组集Cmc1⊆C为G1的1个团,当且仅当Cmc1中的任意两车组c,c′∈Cmc1具有CoAI冲突,团Cmc1为极大团,当且仅当对所有车组c*∈CCmc1,车组集Cmc1∪{c*}中至少存在两不具有CoAI冲突的车组,令CMC1为G1中所有极大团的集合。为避免具有CoAI冲突的车组溜往同一条调车线r,可限制每个极大团Cmc1⊆CMC1中,最多只有1个车组指派给该条调车线,即 (9) 相比于式(8),式(9)中每个约束的变量数最少为2,最多可为车组的数量。因此,式(9)有助于加强整个模型线性松弛的定界能力,加快模型收敛。 (2)编组顺序冲突 在具有特定编组顺序要求的1列出发列车中,其车组由于指定的编组顺序还可能存在冲突,简称编组顺序冲突(Conflict of Block Sequence, CoBS),也不能溜往同一条调车线。例如,某出发列车d有两车组c和c′,假设c 文献[12]考虑出发列车的编组顺序要求,提出了两两编组顺序冲突约束 oc-oc′≤M(2-xcr-xc′r) ∀d∈D2,c,c′∈Cd|c (10) 式(10)可保证各出发列车严格按照指定的编组顺序编成,但该式与式(8)存在类似问题,不利于构建紧凑的数学模型。这里,同样使用图的极大团提出该约束的另一表达式。 类似地,引入另一个无向冲突图G2=(C,I2),其中,顶点集C包括所有车组,边集I2代表车组的CoBS冲突,若车组c和c′具有CoBS冲突,则在这两车组的顶点间构造1条无向边。定义CMC2为G2中所有极大团的集合,索引为Cmc2∈CMC2。对各调车线r,要求在各极大团Cmc2∈CMC2中,最多只有1个车组可在该调车线上集结,由此,可避免同一列出发列车中存在CoBS冲突的车组同时溜放调车线r,即 (11) 式(11)可发挥式(10)相同的作用,但有助于提高该类约束的定界效果。 目前,寻找冲突图中所有极大团的方法已较为成熟,推荐使用文献[14]的算法,对于许多具有上万顶点数的无向图,一般可在几十秒内生成所有的极大团。 2.3.3 连挂约束 模型引入出发列车的编组连挂决策,以较为合理地估计各车组在其对应出发列车的整个编组连挂过程中的走行距离,进而度量各车组的编组连挂成本。根据定义,各出发列车d只有在实际发生第k次连挂后才可能发生第k+1次连挂,该约束可表示为 (12) 在同样的要求下,对于任意出发列车d,只有在其有车组c′∈Cd于第k次连挂时被牵出,才可能有其另外车组c∈Cd于第k+1次连挂时牵出,即 (13) 此外,对于有特定编组顺序要求的出发列车d∈D2,在编组时,还需按指定的车组排列顺序依次连挂调车场里该出发列车吸收的车组。例如,出发列车d∈D2有两车组c和c′∈Cd,假设oc≤oc′,则要求在编组d时,车组c需不晚于车组c′被连挂牵出。该约束为 ∀d∈D2,c,c′∈Cd|oc≤oc′ (14) 通过式(10)或式(11),可使得任意出发列车d∈D2中具有CoBS冲突的车组溜往不同调车线上集结,再由式(14),可对这些车组按要求的排列顺序连挂,从而确保通过简单的溜放和连挂作业便可将各出发列车d∈D2按指定的编组顺序编成。 2.3.4 能力约束 各调车线r∈R具有有限的有效长lr可供车组集结占用,考虑到可能有车组溜放不到位进而在调车线上产生空隙,引入有效长可利用率θr,规定任意时刻在该线路上占用的车组总长不能大于其可利用有效长θrlr。由定义,各车组c∈C在其对应到达列车的解体起时ec开始占用其调车线,在其归属出发列车的编组终时vc释放占用其调车线,即车组c对调车场的占用时段为[ec,vc]。显然,各调车线r∈R上集结的车辆只会在各车组c∈C的占用开始时刻ec和结束时刻vc发生变化,可在各车组c∈C的占用开始和结束时刻引入调车线能力约束。 令T为车组对调车场占用开始和结束时刻的集合,索引为t∈T;δct为0-1变量,若车组c在时刻t占用调车场,取1,否则取0。文献[10-12]提出了以下约束 (15) 式(15)容易理解和实施,但未利用1个有用的特征。任意时刻t∈T同时占用调车场的车组集合(记为Ct)可能与另一个时刻t′∈T的Ct′相同,即Ct=Ct′,甚至Ct⊂Ct′,基于式(15)可能产生许多冗余且不紧凑的约束,影响模型性能。 现利用区间图的极大团对既有的调车线能力约束进行改进。不难看出,车组对调车场的占用时段可诱导出1个区间图G3=(C,I3),其中,顶点集C为所有车组,对任意两车组c和c′∈C,若其对调车场的占用时段相交,即[ec,vc]∩[ec′,vc′]≠∅,则在G3中用1条无向边连接对应顶点c和c′。定义CMC3为G3中所有极大团的集合,由图论可得,G3中各极大团Cmc3∈CMC3是不相同的,且可代表其所包含所有时刻同时占用调车场的最大车组集合。基于CMC3,调车线能力约束可通过要求任意极大团Cmc3∈CMC3在任意调车线r∈R上集结的车辆总长不能超过该调车线的可利用有效长来满足,即 (16) 相比于式(15),式(16)可有效避免冗余约束。事实上,对各调车线r∈R,只需对满足∑c∈Cmc3sc>θrlr的极大团Cmc3∈CMC3建立约束,进而可对式(16)作进一步简化。此外,区间图的极大团生成是易解问题,既有文献存在多项式精确算法[15]可直接使用。 综上,可将技术站调车线运用问题构建为0-1非线性规划模型OCTA 式(1) s.t. 式(2)~式(7),式(9),式(11),式(12)~式(14),式(16) xcr∈{0,1} ∀c∈C,r∈R (17) yckr∈{0,1} ∀c∈C,k∈K,r∈R (18) zdkr∈{0,1} ∀d∈D,k∈K,r∈R (19) 上述模型中,式(7)含1个非线性项xcr·zdkr,为两个0-1变量相乘,容易线性化。采用以下3个线性表达式直接替代式(7) yckr≤xcr∀d∈D,c∈Cd,k∈K,r∈R (20) yckr≤zdkr∀d∈D,c∈Cd,k∈K,r∈R (21) xcr+zdkr-1≤yckr∀d∈D,c∈Cd,k∈K,r∈R (22) 目标函数(1)中还有1个非线性项yckr·zbck′r′,也是两个0-1变量相乘。为此,引入新的0-1变量λcbckk′rr′=yckr·zbck′r′,在目标函数(1)中以λcbckk′rr′替代yckr·zbck′r′,并采用下式维持3个变量的正确关系 λcbckk′rr′≤yckr ∀c∈C,k,k′∈K,k′≥k,r,r′∈R (23) λcbckk′rr′≤zbck′r′ ∀c∈C,k,k′∈K,k′≥k,r,r′∈R (24) yckr+zbck′r′-1≤λcbckk′rr′ ∀c∈C,k,k′∈K,k′≥k,r,r′∈R (25) 由此,模型OCTA可转化为0-1线性规划模型LCTA (26) s.t. 式(2)~式(6)、式(9)、式(11)、式(12)~式(14)、式(16)、式(17)~式(25) λcbckk′rr′∈{0,1} ∀c∈C,k,k′∈K,k′≥k,r,r′∈R (27) 模型(LCTA)是0-1线性规划,既有研究提出了许多高效求解算法,并已集成到主流商业优化软件(例如CPLEX、GUROBI)中。同时,我国典型编组站的统计数据显示,1个调车场一般设置不超过40条线路,1个阶段(3~4 h)集结车组数一般小于100组,出发列车平均连挂次数一般不超过3次,模型(LCTA)的规模是可控的。因此,使用商业优化软件直接求解模型(LCTA),直到获得最优解或者其他预设终止条件达到为止。 本节以文献[10]中的数据为基础构造算例,验证所提出方法的有效性。采用Matlab 9.0编程所提出方法,并调用CPLEX 12.8求解模型(LCTA)。计算环境是CPU为Inter(R) Core(TM) i7-7700 3.60 GHz,RAM为16 GB的个人计算机。 测试技术站的调车场设置10条调车线(R1~R10),用于集结7个去向(1~7)的车辆,调车线信息见表2。 表2 调车线信息 考虑测试车站2个阶段(09:00—15:00)的调车线灵活运用问题。已知到达列车共13列,编号为A0~A12,其中,A0为虚拟到达列车,用于表示阶段初调车场现在车。到达列车解体方案见表3,为便于计算,设置A0的解体起时为阶段开始时刻。出发列车共18列,编号为D1~D18,其中,D13~D18为虚设出发列车,用于分别表示阶段末去向2~7在调车场的残存车。出发列车编组方案见表3,设置D13~D18的编组起时为阶段结束时刻。 表3 列车解编方案 已知车流推算方案见表4,其中,出发列车D5、D6和D12需按照给定的可编去向顺序编组。 表4 车流推算方案 根据表3和表4,可将到达列车划分为67个车组,车组信息见表5。 算例其他参数设置如下。首先,对于单位解体溜放成本α1和单位编组连挂成本α2,由于缺乏相应成本标准,采用调机每车公里油耗费用对这两个参数进行设置。对于α2,鉴于编组连挂全过程需要调机提供动力,产生油耗成本,故令α2=10-7E油耗P柴油Q车≈ 0.004 元/ (车·m),其中,调机每万吨公里油耗E油耗取为 50 kg/万t·km,柴油单价P柴油取为10元/kg,单车质量Q车取为 80 t/车。对于α1,与编组连挂相比,解体溜放过程不需要调机参与,不直接产生调机油耗费用,但是车组在解体溜放全过程中具有的动能是由调机将其推峰积累的势能来提供的,即解体溜放间接产生调机油耗费用,结合这一特点,令α1=0.5α2。其次,令各调车线r的有效长的可利用率θr为1。需指出的是,在实际应用中,可根据考虑技术站的实际情况对α1、α2和θr进行赋值。此外,已知阶段初现在车组C1、C2、C3、C4和C5分别位于调车线R2、R8、R9、R2和R3上,设出发列车最大允许连挂次数|K|为3。 3.2.1 约束建模技术对比 在模型LCTA的建立过程中,使用图的极大团技术对既有溜放约束式(8)、式(10)和能力约束式(15)进行了改进,以期减小模型规模,提高求解效率。为检验改进效果,设置3个替代模型ACTA1~ ACTA3与模型LCTA进行对比分析,其中,ACTA1使用溜放约束式(8)、式(10)和能力约束式(15)建立模型,ACTA2使用溜放约束式(9)、式(11)和能力约束式(15),ACTA3使用溜放约束式(8)、式(10)和能力约束式(16)。 模型对比结果见表6。由表6可见,使用极大团技术改进各约束后,约束数量均有不同程度的减小,较为显著地缩减了模型规模。对于溜放约束式(8),使用式(9)使约束数量减少81.9%,各约束中平均决策变量数从2增加至6;对于溜放约束式(10)、式(11)使约束数量减少86.1%,去除了冗余约束;对于能力约束式(15)、式(16)使约束数量减少26.7%,且将约束中的最小决策变量数由5提高到16。求解效率方面,仅改进溜放约束,求解时间从54.4 s减少至46.1 s;仅改进能力约束,求解时间减少至36.5 s;同时改进两类约束,求解时间减少至36.1 s,缩短率达33.6%,改进效果较明显。综上,采用极大团技术建模溜放约束和能力约束,均有助于缩减模型规模,提高求解速度,且使用该技术对能力约束进行改进的效果更为显著。 表5 车组信息 表6 模型对比 3.2.2 结果分析 测试算例的最优调车线运用方案见图3,图中,峰尾在右端,纵轴表示调车线,横轴表示车组,横轴从右往左表示车组对调车线的占用顺序,更靠近峰尾的车组先占用调车线。方便理解,以调车线R5为例,从图3中可见,归属于出发列车D5的车组C8、C24和C29以及归属于出发列车D12的车组 C32、C40、C56、C62依次占用调车线R5。 最优出发列车编组调车计划见表7,表中,第3列为编组调车计划,由若干连挂钩组成,编组调机根据该计划指定的顺序依次将关联调车线上的车辆连挂牵出,即可将出发列车按规定的顺序编成。例如,为编组有顺序要求的出发列车D5,需首先在调车线R5上连挂去向5的40辆车(来自于车组C8、C24和C29),然后在调车线R7上连挂去向6的24辆车(来自于车组C10、C25和C33),总连挂钩数2钩。 由图3、表7可知,各车组尽可能按固定方案且以最小调车成本使用调车线。例如,对于出发列车D11,只可编入去向1的车辆,其吸收的车组C37、C50、C59和C63全部分配在其固用调车线R1上;对于出发列车D2,可同时编入去向1和2的车辆,去向1的车组C18分配至其固用调车线R1,去向2的车组C5、C19和C21则分配至其固用调车线R3。同时,受调车线能力的限制,部分车组不能在其固用调车线上集结。例如,出发列车D12可编入去向5和6的车辆,去向5的车组C32、C40、C56和C62被分配在固用线路R5上,但去向 6的车组C60和C65则被分配到了调车线R7,尽管未能满足固定使用方案,但尽可能靠近了其固用线路R6,可方便后续编组连挂作业。 统计结果见表8,其中:gap为目标值与最好可知下界的相对间隔;tcost为实际总解编调车成本;rcost为实际总解体溜放成本;rdis为车辆平均溜放距离;pcost为实际总编组连挂成本;pdis为车辆平均连挂距离;frate为按固定方案使用调车线的车辆占比;fint为车辆实际占用调车线与其固用线路的平均最小间距。 图3 调车线运用方案 表7 编组调车计划 表8 统计结果 从表8来看,在采用的单位调车成本下,总解编调车成本为4 942.7元,其中,总解体溜放成本为2 379.9元,占比48.1%,总编组连挂成本为2 562.8元,占比51.9%,表明编组连挂调车作业对总解编调车成本的影响更大。注意,在不同技术站,调车成本的度量可能有所不同,此结论不具有一般性。其次,按固定方案使用调车线的车辆占比达85.5%,车辆实际占用调车线与其固用线路的平均最小间距为1.0 m,达到预期效果,即车辆尽可能占用其固用线路,若不能满足,也尽可能靠近其固用线路,以方便调车工作。求解效率方面,耗时36.1 s将算例求解到最优(即gap为0),能够满足实时决策的要求。可见,模型LCTA具有高质量的求解效果和高效的求解速度,可用于辅助现场技术站调车线灵活运用的决策。 3.2.3 最大连挂次数的影响 出发列车最大允许连挂次数|K|是模型LCTA的输入参数,其取值影响模型的规模和求解性能,本节采用灵敏度分析方法讨论参数|K|的影响。考虑|K|的4种取值,分别为2、3、4和5,在每种取值下,保持其他参数不变,分别以180 s限制时间和求到最优为终止条件,求解模型LCTA,结果见表9。 表9 最大连挂次数的影响 根据表9可得,随着|K|的增大,模型LCTA的规模呈近似二次多项式增长,使得模型的求解难度逐步加大,且在180 s内模型的求解质量呈变差趋势。具体地,当|K|等于2和3时,分别耗时72.0 s和36.1 s便可收敛,与最好目标值(即8 181.6)相比,获得目标值分别增加43.6%和0.0%,注意,|K|取3时,已找到最好解。但当|K|等于4和5时,在180 s内均不能收敛,获得目标值分别增加15.8%和874.7%,事实上,|K|等于4和5时,需分别耗时近8.5 min和2.5 h才能收敛,且找到的是与|K|取3时相同的最好解。可见,参数|K|同时影响模型的求解质量和时间,在实际应用时,需结合对解质量和实时决策的需要,采用例如本节提出的灵敏度分析等方法合理设置|K|的取值。 3.2.4 调车线占用权重的影响 车组对调车线的占用权重wcr也是模型LCTA的输入参数,本节在2.2节取值规则的基础上,提出3个新的规则,以此讨论wcr的影响。与现规则相比,规则1加强按固定方案使用调车线的要求,增大(车组对非固用调车线的占用权重)wcr,对各车组c,若调车线r∉Fc,令wcr=2 min{grr′,r′∈Fc};规则2弱化调车线固定使用的要求,减小wcr,对各车组c,若调车线r∉Fc,令wcr=2 min{grr′,r′∈Fc}/5;规则3忽略调车线的固定使用方案,规定各车组c占用各调车线的权重wcr均为1。在各规则下,保持其余参数不变,终止条件分别取为180 s限制时间和求到最优,求解模型LCTA,结果见表10。 表10 调车线占用权重的影响 从表10可发现,随着wcr的减小,调车线运用方案的总解编调车成本tcost呈减小趋势,但按固定方案使用调车线的车辆占比frate也呈下降趋势,使得该方案可能缺乏规律性,与固定使用方案的要求存在较大出入,不利于实际实施。具体来讲,对于tcost,相比于规则1,wcr按现规则取值时,最优的tcost无变化;按规则2取值时,最优的tcost减小3.8%;按规则3取值时,尽管未找到最优解,但在180 s内获得的tcost仍减小4.8%。对于frate,相比于规则1,现规则下最优解的frate无变化,规则2下最优解的frate的增加量为0.02%,规则 3下最好解的frate的减小量达73.2%。此外,伴随wcr的减小,模型LCTA的求解难度逐渐增大,当wcr按规则1和现规则取值时,均能在180 s内求解到相同的最优解;但当按规则2和3取值时,只能在180 s内找到gap分别为7.7%和21.1%的可行解,此时为寻找最优解,规则2下需耗时486.7 s,规则3下将遇到内存越界,无最优解返回。主要原因是车组对不同调车线的wcr越接近,将使得模型LCTA中解的对称性增强,进而增大模型的求解难度。可见,wcr的取值同时影响模型的求解效果和性能,小的wcr有利于减小总解编调车成本,但不利于维持调车线运用的规律性,还会增大模型LCTA的求解难度。为尽量满足现场的调车线固定使用要求,应给wcr取较大的值,以在求解效果和效率上取得好的折中。 本文提出了铁路技术站在作业计划编制阶段的调车线灵活运用的优化方法。在对调车线运用问题进行分析的基础上,以总加权解编调车成本最小为目标,考虑车组溜放和连挂、出发列车编组顺序和调车线能力等要求,构建0-1线性规划模型,并使用基于图的极大团技术对其中的溜放约束和能力约束的既有建模方法进行改进,以减小模型规模,加快求解速度。算例结果表明,所提出方法可在合理时间内获得总加权解编成本低且容易被现场接受的调车线运用方案,能够为技术站灵活运用调车线提供决策支持。 本文侧重于研究调车线灵活运用的线性优化模型,该模型的规模随调车线与车组的数量以及最大连挂次数呈多项式增长,可能给求解带来挑战,针对大规模问题,研究有效的调车线灵活运用算法,是下一步将开展的工作。其次,本文对车组的溜放和连挂走行距离做了近似估计,接下来可研究这两个参数更加准确的度量策略,以进一步提高所提出的调车线运用模型的理论与实际价值。接着,在现场,调车线运用方案的可行性可能受解编调车进路安排的影响,未来可研究调车线运用与调车进路安排综合优化问题,提高调车线运用方案的兑现率。此外,在编制技术站作业计划时,调车线运用与车流推算和列车解编排序相互影响,探讨三者集成优化,解决作业计划整体编制问题,也是将来值得研究的方向。2.4 整体模型及线性化
3 算例分析
3.1 算例设置
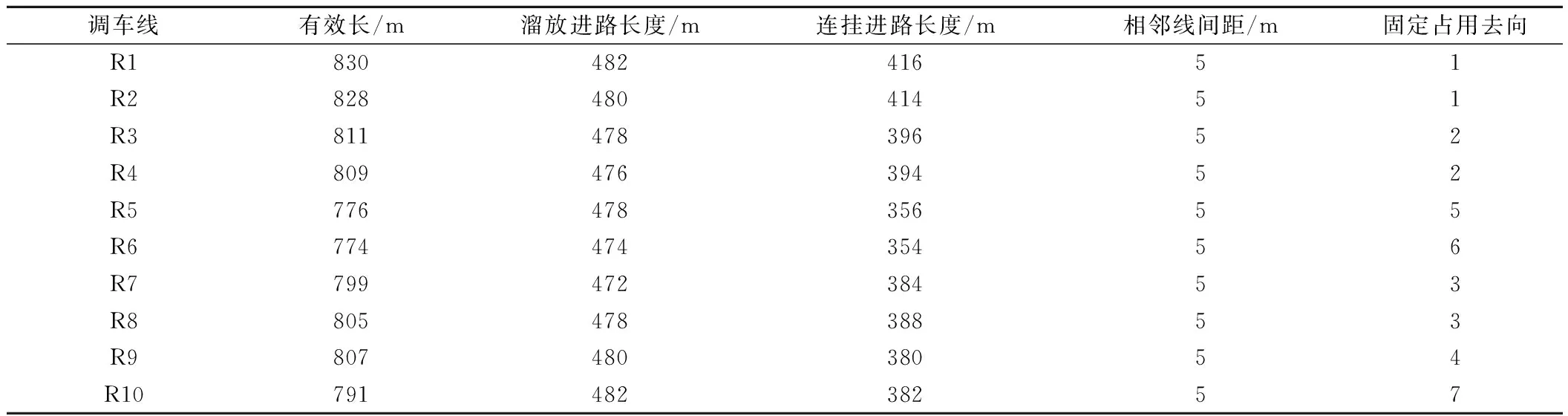


3.2 计算结果





4 结论

