运用条件下城轨车辆转向架构架疲劳寿命研究

王斌杰，谢树强，齐延辉，李 强，姜朝勇，董 磊

(1.北京交通大学 机械与电子控制工程学院，北京 100044; 2.中国国家铁路集团有限公司，北京 100844；3.中车长春轨道客车股份有限公司 转向架开发部，吉林 长春 130062)

城市轨道交通目前已成为城市建设与发展的重要交通方式，车辆安全性和关键结构疲劳可靠性成为保障完成繁忙运输任务极为重要的因素。转向架构架作为走行部的重要结构，主要以数值模拟仿真计算和台架试验来确保构架疲劳寿命满足运用要求(图1)。同时，构架设计制造单位也在不断优化改进构架结构以期在轴重与接口限制条件下提升构架疲劳可靠性。针对轨道车辆结构疲劳强度，广泛采用的方法是研究其疲劳性能，利用国际规范[1-8]进行评价。文献[9-14]采用模拟计算和台架试验方法研究标准载荷工况下转向架构架的疲劳性能，结果显示构架应力满足安全性要求，但由于条件所限未能开展基于大量运用数据的疲劳可靠性研究，导致预测的构架应力未能反映实际运用中的损伤状况。文献[15]分析了依据UIC规范进行DMU构架抗疲劳设计不能满足安全运用要求，定性分析了运用条件和焊接接头质量是导致构架发生疲劳裂纹的直接原因。文献[16]验证了提速客车的运用条件要严酷于设计规范的情况，导致构架疲劳强度不足而产生疲劳裂纹。文献[17]研究了线路条件与等级对构架疲劳损伤的影响，并且分析了运行速度对于构架疲劳的贡献。文献[18]分析了模态应力对于构架疲劳损伤的影响，表明模态应力将缩短构架的使用寿命。

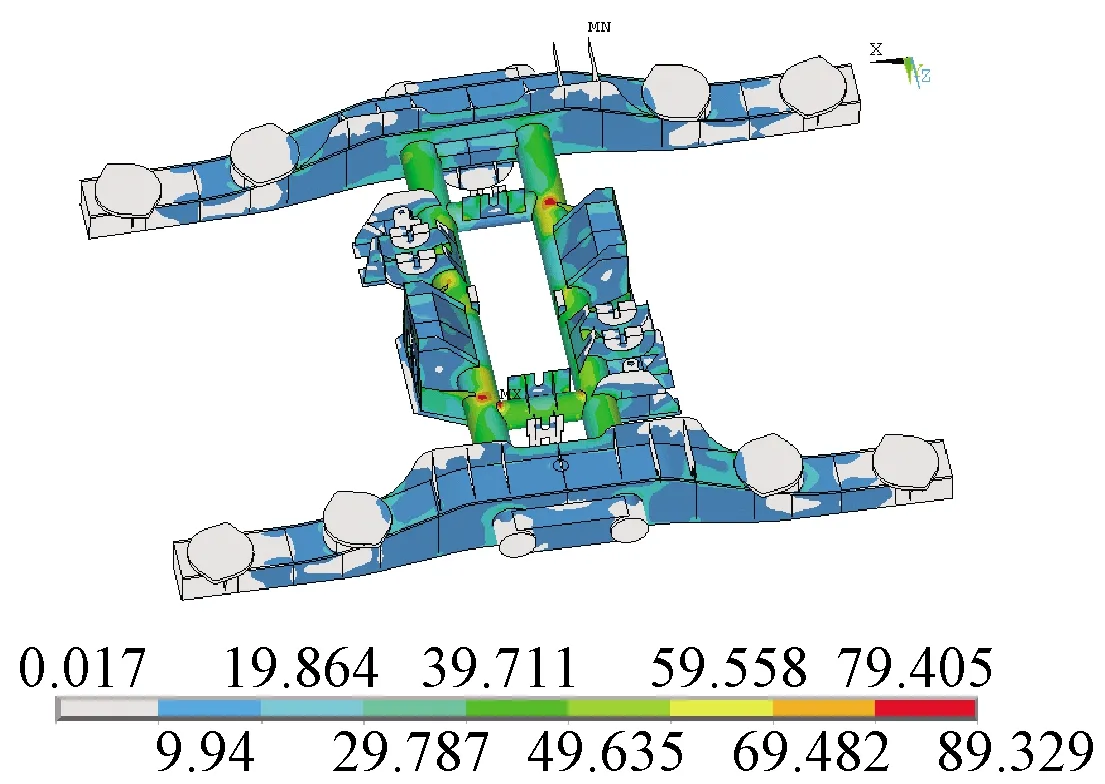
图1 构架疲劳数值模拟仿真(单位：MPa)

分析构架运用安全性的更有效方法是开展构架在实际运用状态下进行疲劳控制部位的动态应力测试与分析。因此，为确保运用安全，同时为制定以可靠性为中心的构架检修周期提供依据，迫切需要分析构架在运用中的疲劳损伤累积状况并确定构架的安全运用寿命。本文在真实运行条件下开展跟踪测试，获得了构架疲劳控制部位的动应力状况、轴箱加速度、车辆速度、车辆横向摇头角速度等信息，进行了基于真实运用条件的构架疲劳损伤与可靠性研究。

1 测试线路与测试内容

研究车辆为线路实际运行车辆，全线共计18个区间，车辆按调度计划于内环与外环运行，车辆每次驶入正线时均与上一次的车头方向相反，如图2所示。

图2 车辆运行线路

试验构架为一个新造构架，换装于被试车辆。在构架疲劳控制部位布置电阻式应变片用于获取运行中的构架动应力，在轴箱体上方布置垂向加速度传感器用于反映转向架所受到的线路动态激扰，在车体下方布置测速雷达与陀螺仪传感器，用于获得车辆的运行速度、直线、曲线等线路信息(图3)。将测试设备封装于车体下方，车辆运行供电后，所有被测数据会自动实时存储。

图3 轴箱加速度传感器与测速雷达安装

被测车辆始终按照正常运用计划上线运行，每日测试数据累积6 GB左右。所测数据涵盖了车辆全运营工况，能够完全涵盖所测物理量在真实运用条件下的特征。

2 线路实测等效应力

2.1 S-N曲线及疲劳极限

针对不同形式的焊接接头，确定了足够安全的平均缺口应变幅，对应的单轴应力幅为105 MPa[19-20]。文献[21]研究得到了不同破坏概率与中值许用应力之比。参考以上文献及文献[22]选用了幂指数S-N曲线(式( 1 ))，所研究焊接接头在可靠度为99%时，对应于200万次应力循环的疲劳极限为70 MPa。

σmN=C

( 1 )

式中：σ为应力幅值；m为焊接接头S-N曲线常数，文中取3.5；N为应力循环次数；C为常数。

2.2 等效应力与损伤计算

实测的应力-时间历程经雨流计数后获得各测点的应力谱，基于S-N曲线，采用Miner累积损伤法，由式( 2 )求得等效于构架全寿命里程的200万次作用等效应力幅(以下统称等效应力)。

( 2 )

式中：σaeq为等效应力；L为全寿命要求运用公里数；L1为实测公里数；ni为各级应力幅值的循环次数；σai为各级应力幅；m为材料或焊接接头S-N曲线常数。

对应于任一天的动应力数据，有

( 3 )

基于实测的每日损伤累积，按照预计运用里程的疲劳累积损伤为

( 4 )

式中：L=360万km；ld为第d天的测试里程。

对应于预计运用里程的等效应力为

( 5 )

式中：σeqj为第j个测点在测试总天数w内的等效应力；N为360万km的作用总频次，文中为200万次。

图4示出了具有较大等效应力电机吊座与横梁连接区域A-3、A-4与横侧梁连接区域A-1、A-2的等效应力与疲劳极限的比值。按照等损伤法则，应力幅的增大将缩小结构的疲劳寿命。若等效应力为疲劳许用应力的1.6倍，则疲劳寿命将缩小为设计寿命的19.3%。

图4 构架A疲劳控制部位与等效应力计算结果

3 构架疲劳可靠性计算

应力-强度干涉理论作为机械产品安全性分析方法，可以统计产品应力的概率密度分布、疲劳强度概率密度分布，获得相对应的干涉模型，继而求出产品的可靠性[23-26]。假设每天的实测等效应力服从正态分布，构造的检验统计量W为

( 6 )

其中

( 7 )

( 8 )

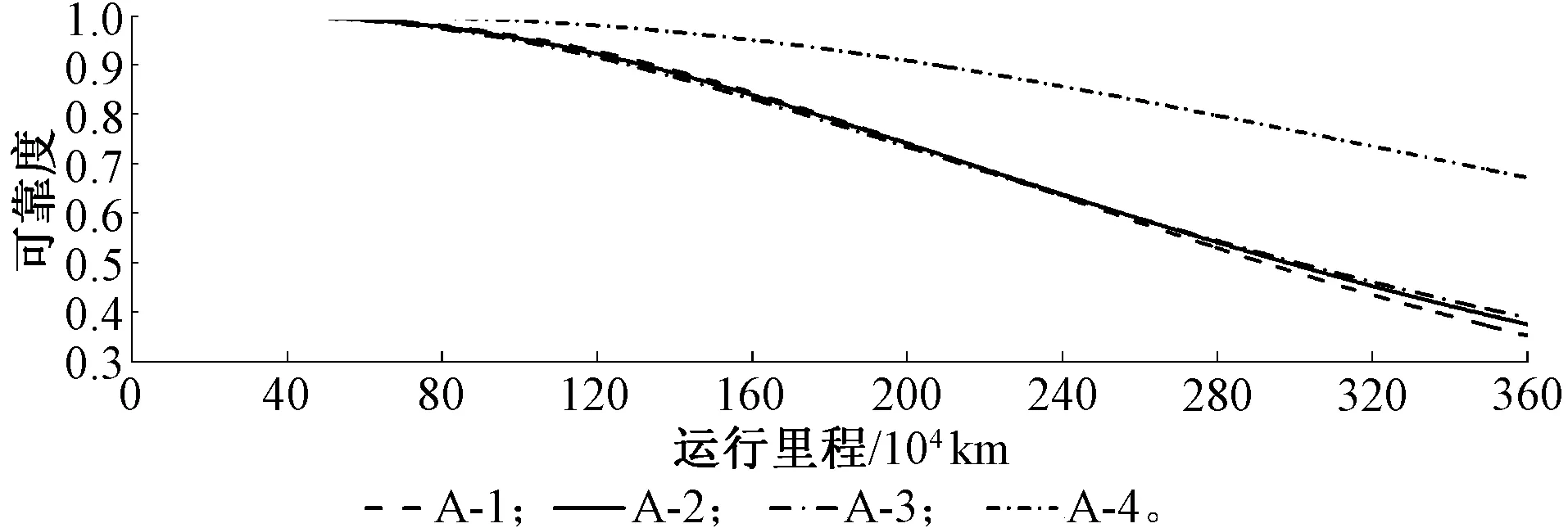
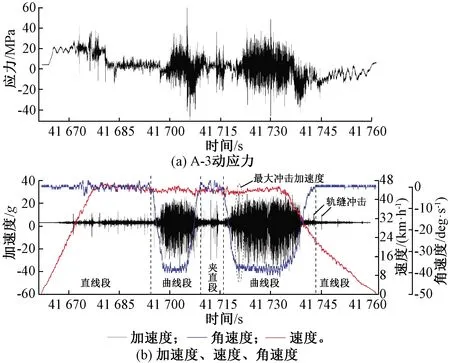
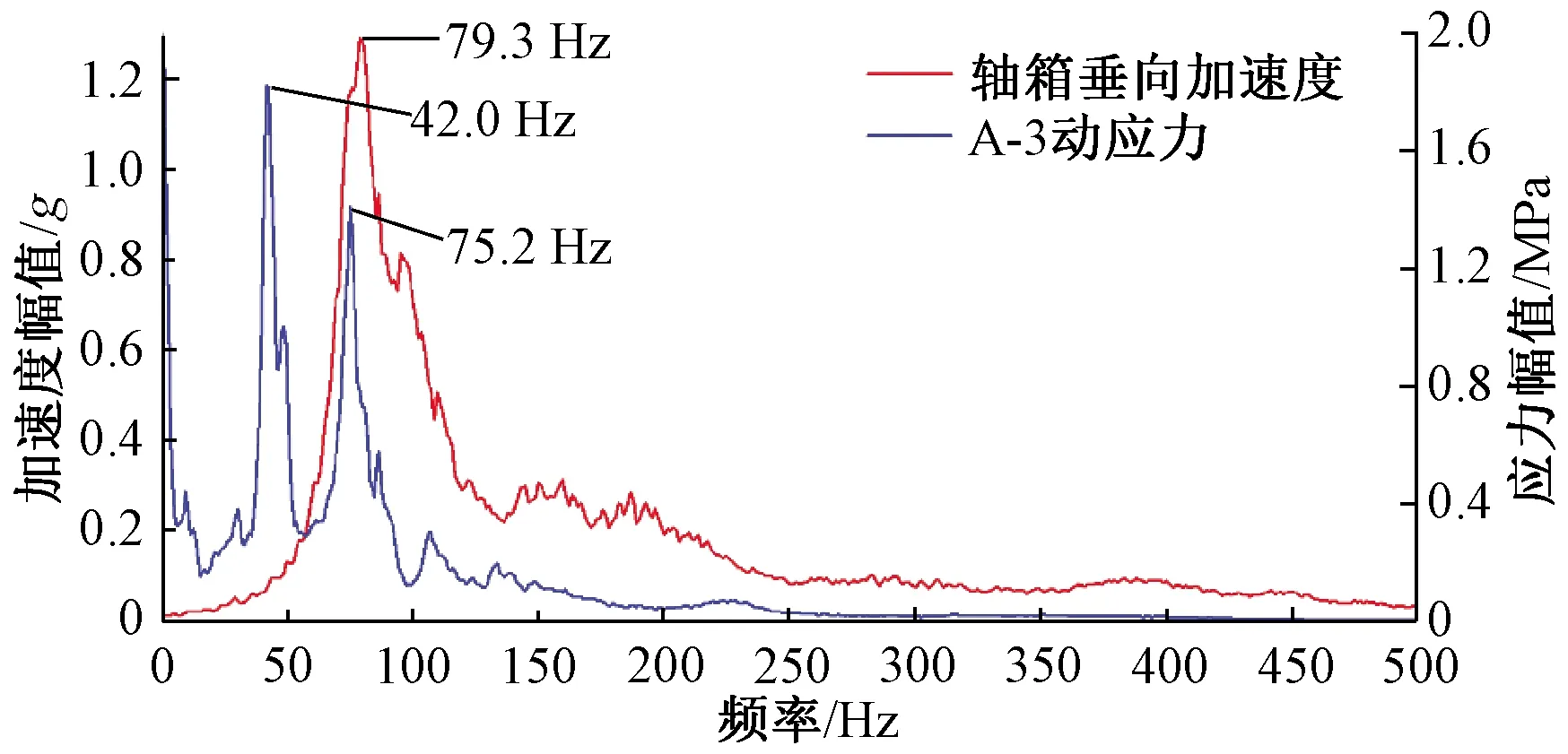
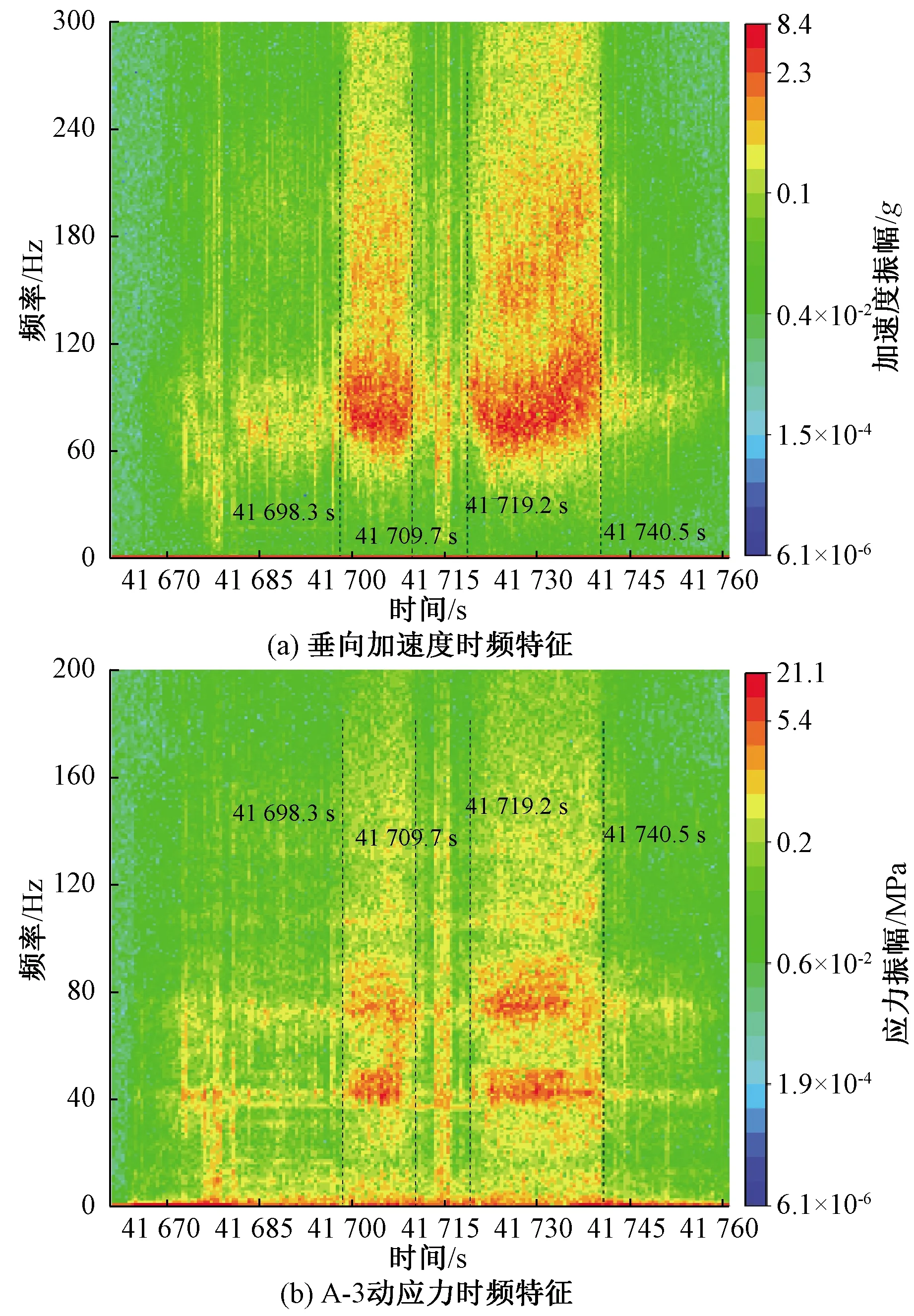
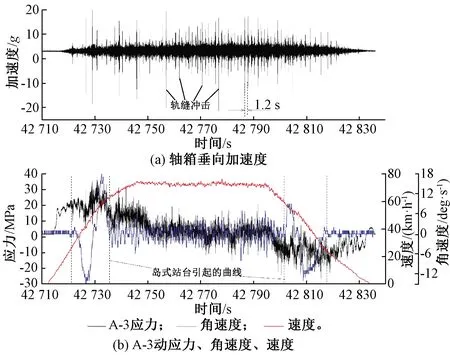
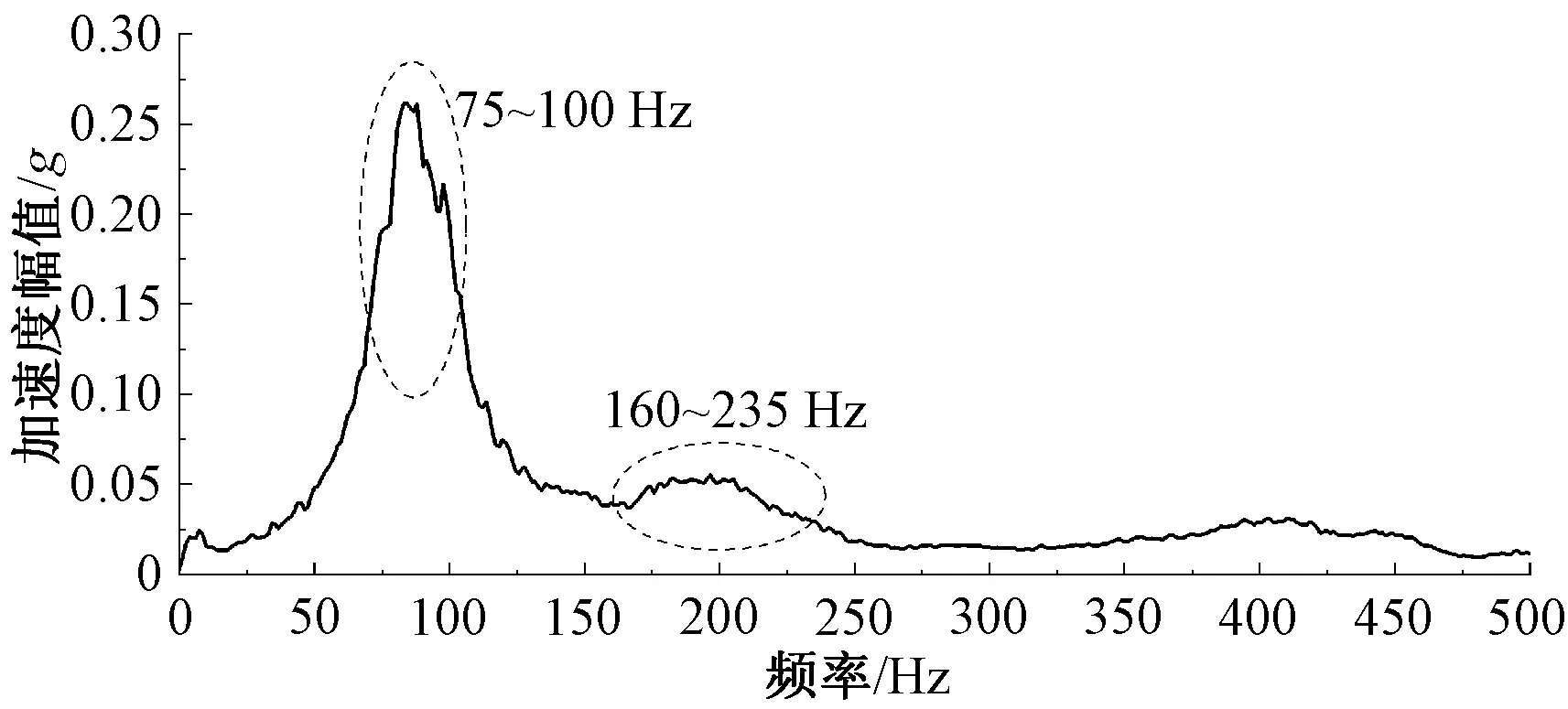
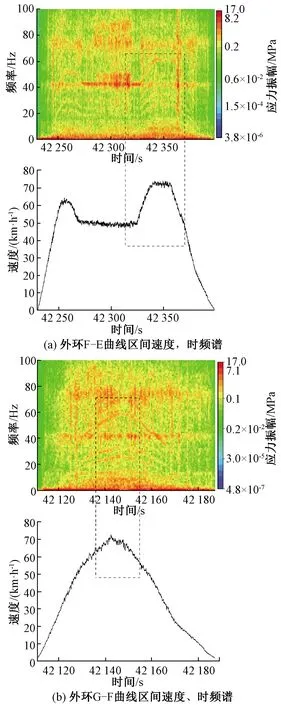
取α=0.01(99%的置信水平)，查Wα分位数表可知Wα=0.929，计算得到统计量Wα=0.929

为了更直观展现数据的正态性，以A-1为例，根据对实测等效应力值分组统计画出其概率密度直方图，并得到拟合曲线，如图5所示。

图5 等效应力概率密度统计

通过正态分布非线性拟合获得其概率密度函数的估计值，其均值μ=114.6，标准差σ=3.04。

( 9 )

在文献[22]中确定了和构架同类的焊接接头在确定服役寿命条件下的疲劳强度概率密度函数

(10)

可得可靠度为

(11)

根据式(11)，得到构架疲劳控制部位的应力-强度干涉图，如图6所示。

图6 应力-强度干涉关系

由图6可见，在相对固定的车辆运用环境与线路激扰条件下，构架受载及疲劳控制部位的应力水平较为稳定，从而使计算得到的等效应力分散性小于规范规定。

由t分布和卡方分布理论可知，均值μ与标准差σ的置信区间分别为

[μmin,μmax]=

(12)

(13)

式中：μmin为均值μ置信区间下限；μmax为均值μ置信区间上限；σmin为标准差σ的置信区间下限；σmax为标准差σ的置信区间上限。

当运行里程L未知时，等效应力即变成包含L的表达式，由式( 9 )得到构架随运行里程L变化的等效应力概率密度函数为

(14)

构架随运行里程L变化的可靠度为

(15)

计算R(L)得到可靠度随寿命的变化曲线，如图7所示。

图7 构架疲劳控制部位可靠度曲线

由图7可见，A-1、A-2、A-3三个部位的可靠度低于A-4的可靠度；在240万km之前A-1、A-2、A-3三个部位的可靠度基本相同，随着运用里程的增加，可靠度最低的部位是A-1；对应于99%可靠度，构架的运用里程为40万～60万km，与实际运用调研情况相符。随着运营里程的增加，构架可靠度将发生明显下降，在360万km的设计寿命条件下，最低约0.34，A-4处的可靠度也将降到0.67。

4 构架运用中的疲劳损伤

车辆运行中复杂的轮轨激扰导致不同线路特征下的疲劳损伤累积有显著差异。图8为基于18个区间的应力-时间历程计算得到的A-3等效应力幅。由图8可见，车辆运行于不同区间时等效应力幅具有显著差异，最大等效应力幅为160.4 MPa，位于J—I曲线区间；最小等效应力幅为51.7 MPa，位于C—B直线区间。等效应力幅峰谷值比为3.1，疲劳损伤的差异达到52.5倍。较大的区间损伤差异表明，尽管是一条完整的线路，但存在复杂多变的轮轨激励。

图8 站间等效应力幅值

4.1 高频激扰

选取J—I区间的数据示于图9，分别为A-3动应力、轴箱垂向加速度、车辆摇头角速度、列车运行速度信号。时域内，轴箱加速度、动应力的响应在曲线段均明显强于直线段，响应信号与摇头角速度在时域基本对应，说明曲线段构架的响应更为剧烈。曲线段中，线路对车轮的最大冲击加速度达到40g以上，应力峰值达到60 MPa；相同运行速度运行于直线段时，轮轨激扰主要来自于轨缝冲击。运行于曲线时的轮轨激扰完全覆盖了轨缝的冲击，具有高频次、高幅值的特点。

图9 运行于外环J—I曲线区间时的实测信号

图10 运行于外环J—I曲线区间时A-3动应力及轴箱垂向加速度频谱

将J—I区间的A-3应力信号和轴箱垂向加速度做快速傅里叶变换，如图10所示，加速度的主频约为79.3 Hz，构架应力的主频约为42 Hz和75.2 Hz。图11为轴箱加速度与应力的时频特征结果，在整个站间的两个曲线段内始终存在较高能量，其中轴箱加速度的频率范围为68～102.5 Hz，应力信号的频率为37～51 Hz和69～81 Hz。由图9～图11可见，正线运行中列车速度基本不变，在曲线段加速度和应力均出现了高频次高能量激扰，结合地铁线路特征[27]，推断曲线段存在波磨，从而形成了对车辆持续、周期性的轨道激励。

图11 运行于J—I区间时A-3动应力及轴箱垂向加速度时频特征

选取曲线段内41 724.9～41 725.9 s轴箱加速度信号，进行经验模态分解[28](Empirical Mode Decomposition，EMD)，获得该段加速度信号的固有模态(Intrinsic Mode Function，IMF)分量，如图12所示，其中Signal为轴箱加速度原始信号，IMF1～IMF10为由高频到低频提取的轴箱加速度信号固有模态分量，RES为残差。依据文献[29-31]的研究结果可知，若检测信号EMD分解后的经验模态分量中出现波浪形振动模态，则可确定，在曲线站间的曲线段内存在轨道波磨，如图12中IMF3分量红框中所示。

图12 轴箱加速度1 s信号EMD分解后IMF分量

J—I区间轴箱垂向加速度的主频在68～102.5 Hz范围内，车辆速度范围为30～45.5 km/h，由式(16)可计算得到在该区间的曲线段内波磨的波长为81.3～185.9 mm。

(16)

式中：f为波磨频率；v为列车运行速度，km/h。

4.2 轨缝影响

图13 运行于直线区间时加速度、摇头角速度、列车速度、A-3动应力

图14 运行于直线区间时轴箱垂向加速度频谱

4.3 运行中的转频

电机转频及车轮多边形产生的激扰为与速度有关的物理量，A-3测点的应力信号在不同站间的时频谱中皆存在随速度变化的高能量频率。选取较为明显的两个区间结果示于图15。设电机转频[32]为f1，车轮多边形激扰频率[33]为f2，其表达式为

(17)

(18)

式中：D为车轮直径(0.84 m)；i为齿轮箱传动比(7.69)；v为车辆运行速度，m/s；n为车轮多边形阶数，一般情况下，地铁车辆多边形取为8～9阶[34]。

图15 运行于直线、曲线站间时应力测点A-3时频谱图及速度

基于图15中虚线框中的频率及速度数据，计算电机转频及车轮多边形激扰频率的范围列于表1。对比表1中车轮多边形激扰频率、电机转频与实测频率，车轮多边形激扰频率范围很好的涵盖了实测结果，而电机转频变化范围无法完全覆盖实测范围，可确定车辆多边形激扰将引起构架与速度密切相关的应力响应。

表1 电机转频、车轮多边形激扰频率及实际频率范围 Hz

5 结论

围绕城轨车辆转向架构架运用疲劳可靠性及其影响因素，基于实测物理量，计算构架疲劳控制部位的可靠度，初步研究了运行中不同激扰对构架疲劳损伤的对应情况，得出以下结论：

(1)在99%可靠度下，构架高可靠度运用里程与设计里程具有差距，99%可靠度下构架的疲劳寿命为46.5万km，与实际运用情况吻合；设计寿命360万km对应的构架可靠度为0.34左右。

(2)不同区间线路条件对构架疲劳损伤的影响不同，曲线区间的疲劳损伤明显大于直线区间。

(3)曲线段的轮轨激励复杂，构架出现高频次高幅值的动应力响应，直线区间的轮轨激扰主要来自轨缝冲击，构架动应力响应的频次和幅值都相对较小；车轮多边形也会对构架疲劳损伤形成贡献。

(4)若按照360万km设计使用寿命使用车辆，构架可靠度将发生明显下降，可靠度模型为优化检修周期结构、制定规定可靠度下的构架检修提供了数据基础。

后续将深入研究在实际运用中轮轨激励对构架疲劳损伤的定量表征以及系统提升构架疲劳可靠性的方法，并开展相关的试验验证。