高速列车型面不同磨耗状态下的过岔性能研究分析

肖 乾，李 超，昌 超，孙加林

(1.华东交通大学 载运工具与装备教育部重点实验室，江西 南昌 330013；2.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；3.中国铁道科学研究院 铁道科学技术研究发展中心, 北京 100081)

道岔是铁路上最易损坏的部件之一。道岔的结构比较特殊且相对脆弱，因此在研究车辆振动特性时应与正线轨道区别对待。高速列车长期在线路上运营，在牵引、制动等工况的作用下，车轮型面不可避免会发生磨耗。其中最为常见的车轮磨耗形式便是踏面圆周凹形磨耗。在列车高速运行的情况下，车轮磨耗会对轮岔以及轮轨之间的动态相互作用产生较大的负面影响，进而影响列车的动力学性能。因此研究车轮型面在不同磨耗状态下的过岔性能，对提升高速列车运行的安全性和稳定性有积极作用。

目前，国内外学者对车辆-道岔耦合动力学开展了大量的研究工作，取得了一系列重要研究成果。文献[1]提出Semi-Hertz接触方法，相较于以往的方法能更精确地模拟轮岔滚动接触作用。文献[2-3]通过对比两种类型的车辆模型与道岔的动态耦合关系，认为轨道为刚体时，达到了与预期一致的效果，并求出扩展频率范围内系统动力响应的时域解。文献[4]通过轮岔有限元模型深入研究道岔钢轨破坏机理，得到了影响道岔寿命最重要的两个因素是车辆的过岔速度和车辆轴重的结论。文献[5]为了探究不同的道岔形状、尺寸以及车轮型面对轮岔作用的影响，利用多体动力学软件Simpack建立了4种车轮型面和两种道岔的模型，进行了详细的分析。文献[6]深入研究了铁路道岔轮岔接触的几何关系，对轮岔多点接触的计算和判断方法进行了详细说明。文献[7-8]系统研究了高速铁路和重载线路两种道岔情况下的车岔线桥相互作用规律。文献[9]通过仿真对比分析了单开道岔侧线尖轨不同结构形式下各个轮岔作用的响应特点，为尖轨的减磨设计提供了理论依据。文献[10]通过迹线法和有限元法研究了车轮与道岔钢轨的磨耗问题。文献[11]利用Simpack与Abaqus软件联合仿真，建立了车岔桥刚柔耦合动力学分析模型，全面分析了高速列车直向和侧向经过道岔时车辆、桥梁和道岔的动力学特性。总体来看，上述研究成果推动了道岔区轮轨和车辆轨道动力学的发展。但上述研究较少涉及以下两个方面的问题：一是车轮磨耗引起的轮岔相互作用问题；二是不同里程下磨耗型面对轮岔的作用规律。

文献[12-15]开展了关于轮轨型面磨耗对车辆动力学、轨道动力学特性影响的相关研究工作，但关于车轮型面磨耗对车岔作用的研究相对较少。本文采用数值模拟方法，采用多体动力学软件UM, 以350 km/h客运专线60 kg/m钢轨18号高速道岔和国内某型号高速列车为研究对象，建立车辆-道岔耦合动力学模型，考虑不同里程下的车轮磨耗型面，利用轮轨非椭圆多点接触算法，系统研究不同等级速度下通过18号高速可动心轨道岔的振动特性。

1 变截面道岔模型与车轮型面磨耗实测分析

1.1 变截面道岔模型

图1所示为单开道岔，单开道岔结构包括撤叉区、转辙区和连接部分。高速列车在单开道岔线路行驶时，钢轨截面是实时变化的，同时钢轨的结构特性如高度、廓形、轨顶宽度也会实时变化。钢轨结构的不断变化，不可避免会增加钢轨的振动。如图2、图3所示，通过轮轨型面测量仪得到高速铁路线路道岔各处截面的数据，将得到的数据通过拟合处理获得道岔的空间结构外形。变截面钢轨的拟合处理示意图如图4所示，在变截面道岔模型中对钢轨截面形式变化等非线性特征进行了考虑。在建模过程中还参考了18号道岔的现实尺寸情况，创建了完整的右开道岔swt格式文件。 18号道岔各关键截面参数见表1。

图1 道岔区间示意图

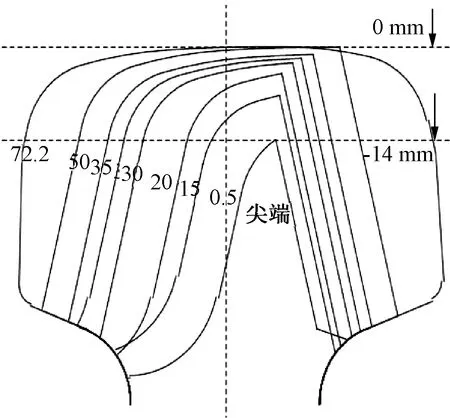
图2 尖轨CAD图示

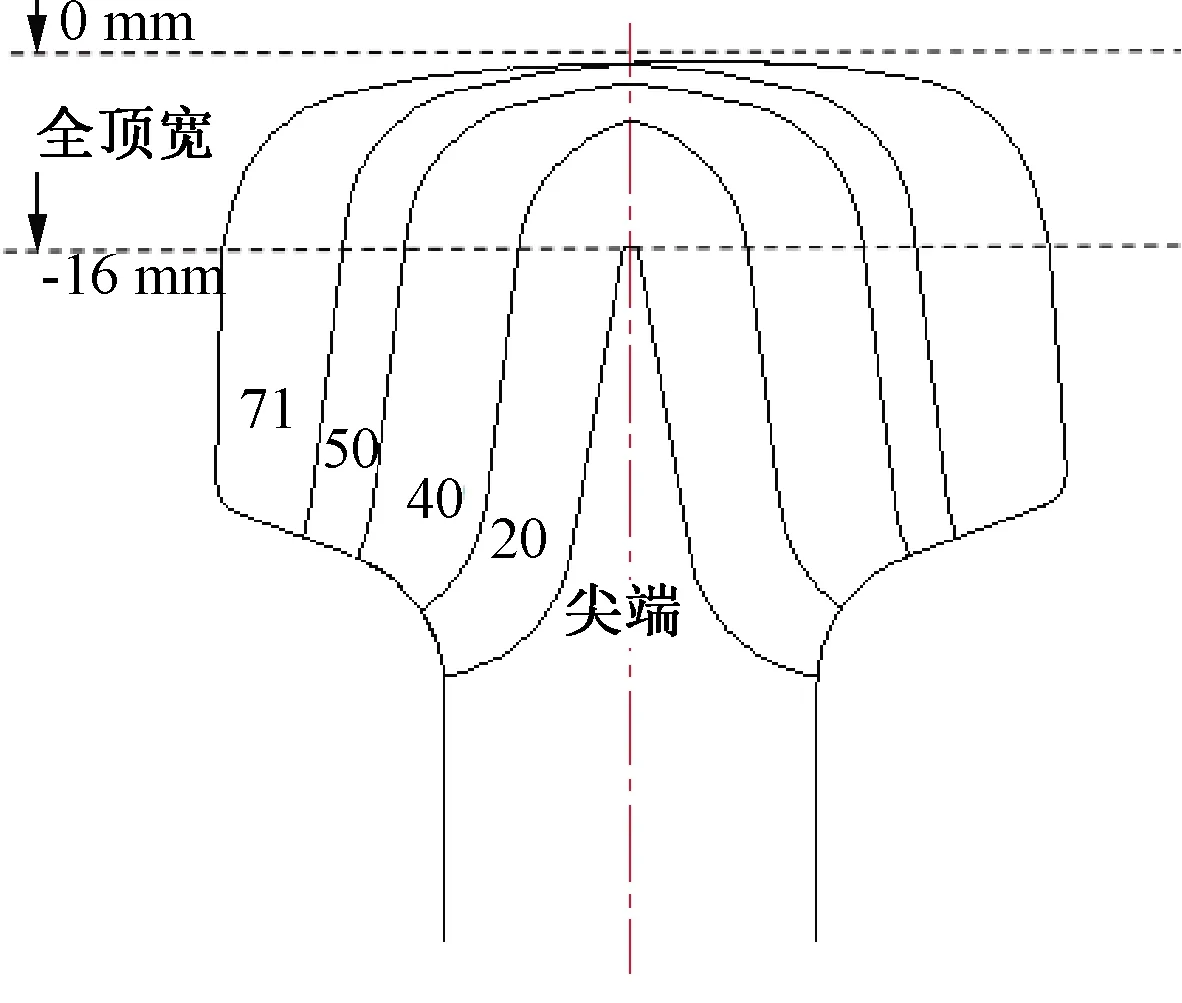
图3 心轨CAD图示

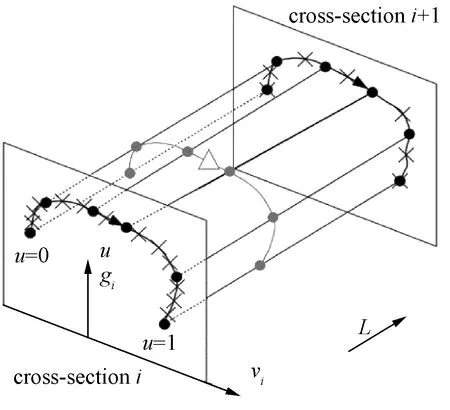
图4 变截面钢轨拟合示意

1.2 车轮型面跟踪实测与磨耗特性分析

通过对该型号动车组车轮型面的磨耗情况进行跟踪实测(图5、图6)，选取测试的运营里程数分别为11.6万、15.3万、20.8万、25.3万km，平均间隔里程约5万km。规定距轮缘内侧70 mm处为车轮圆周磨耗数值的测量位置。所测试的4个运营里程阶段的车轮磨耗深度见表2。将现场实测型面曲线与初始型面曲线(图7)进行对比，可以得出车轮的磨耗主要分布在两个区域：轮缘直线区域和名义滚动圆附近区域。

表1 18号高速道岔变截面钢轨各关键截面参数 mm

型面磨耗的分布范围与运营里程数关系不大且基本固定；磨耗深度和运行里程关系较大，运行里程越大磨耗越深。车轮的轮缘位置处有轻微的磨耗且主要的磨耗形式为圆周凹形磨耗[12]。

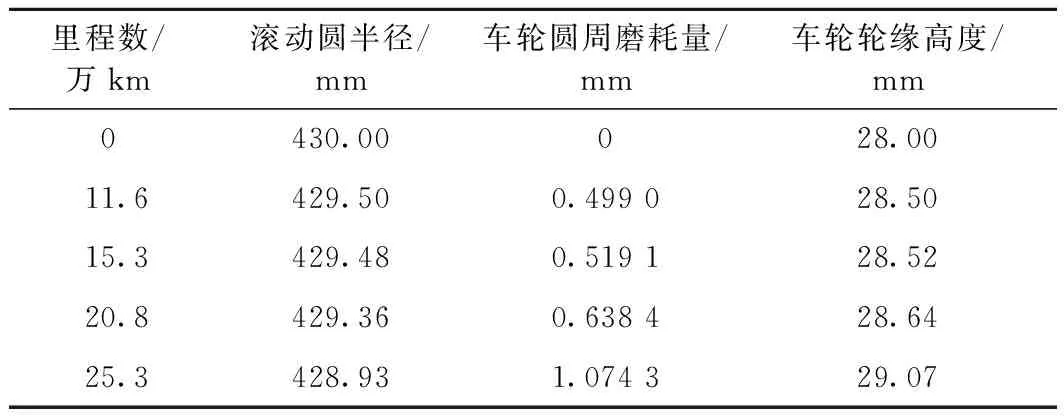
表2 车轮型面磨耗情况统计

图5 车轮型面现场测试

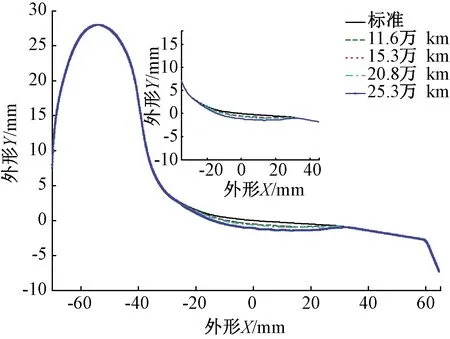
图6 LMA实测不同运营里程下的磨耗型面

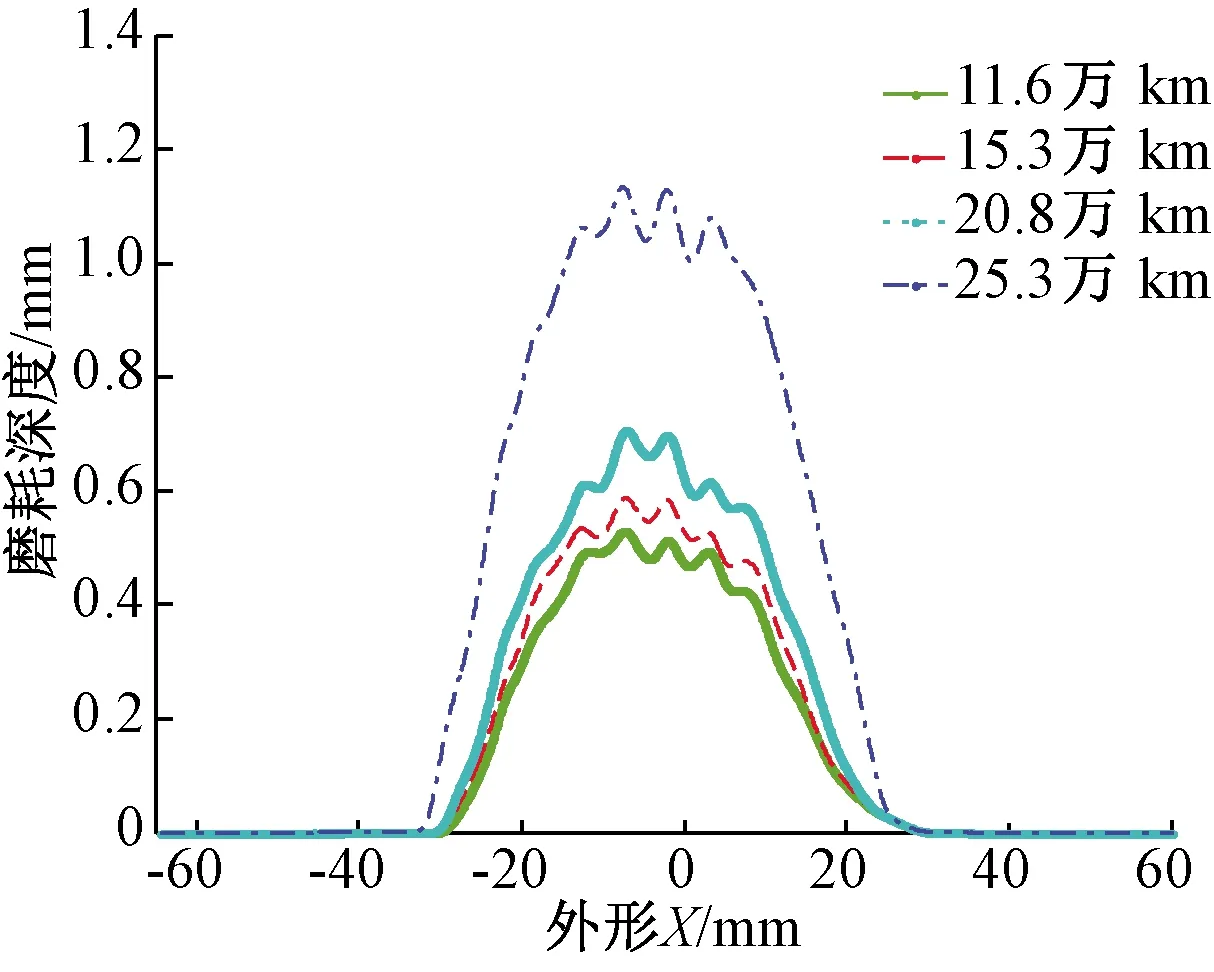
图7 车轮型面不同位置磨耗深度示意

2 车辆-道岔耦合动力学模型

2.1 车辆系统动力学模型

在动力学软件UM中建立50自由度的高速列车车辆模型，模型中共15个刚体，刚体的种类、数目以及各刚体的自由度见表3。在利用UM软件建模时，弹簧、减振器等元件均忽略了其质量，以力元的形式代替。例如空气弹簧使用的力元为Bipolar force，同时综合考虑阻尼；一系钢簧使用的力元为Linear force；转臂节点使用的力元为Special force。动力学模型使用的基本轨为CHN60钢轨，车轮踏面类型为LMA。将拟合处理好的道岔线型输入至UM软件中，图8所示为建立好的车辆-道岔耦合动力学体系。

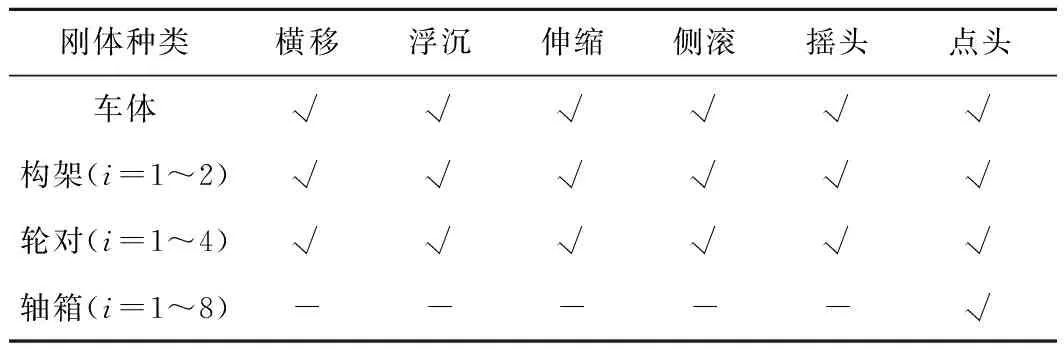
表3 刚体种类及自由度

图9 无磨耗型面与磨耗型面轮岔接触特性对比

图8 车辆-道岔耦合动力学模型

2.2 轮轨滚动接触力学模型

研究表明，列车在转辙区域行驶过程中，将会由开始的基本轨缓慢过渡至尖轨。同时为使列车安全平稳驶过道岔，钢轨的结构会随着行驶状态的改变而变化。图9(a)、图9(c)为初始型面顶宽分别为30、50 mm的接触点分布图。图9(b)、图9(d)为运行25万km，顶宽分别为30、50 mm的磨耗型面接触点分布图。从图9可知，轮轨型面磨损时，轮轨接触部分容易发生多点接触。由于接触斑区域内的车轮和钢轨曲率不是常数，不再满足赫兹接触理论的假设条件[16-17]。为更准确模拟轮轨接触状态，同时满足工程上计算效率的需求，本文采用文献[16]提出的基于虚拟渗透法的轮轨非椭圆多点接触算法(简称K-P算法)。

K-P算法中考虑轮轨接触的法向接触应力pz为

( 1 )

渗透区域的函数为

( 2 )

h(y)=zw(y)-zr(y)

( 3 )

式中:δ0为渗透量；h(y)代表x=0界面上轮轨型面曲线zw(y)、zr(y)两点间距离。接触斑近似服从

( 4 )

由此可通过积分得到

( 5 )

其中，yl表示在y方向的接触斑边界。

则(0,0)处的法向变形位移w0为

( 6 )

可知(0,0)处的渗透值为δ0=2w(0,0)=2w0，由此可得

( 7 )

( 8 )

如图10所示，若轮轨处发生多点接触，根据接触点的渗透量δ0、δi，可求解出轮轨法向力N1、Ni。

计算出轮轨接触的法向接触力以及间隙量后, 可以利用FASTSIM算法得出任意轮轨接触区域上的切向蠕滑力。以80 km/h侧向过岔作为研究对象，分别应用CONTACT、FASTSIM、K-P三种算法进行对比计算。根据图11、图12以及表4的计算结果可知，K-P算法的计算结果精度高，同时通过计算统计可知，K-P算法的计算效率比CONTACT算法高。从数值分析可知，K-P算法和CONTACT算法的计算结果相近。

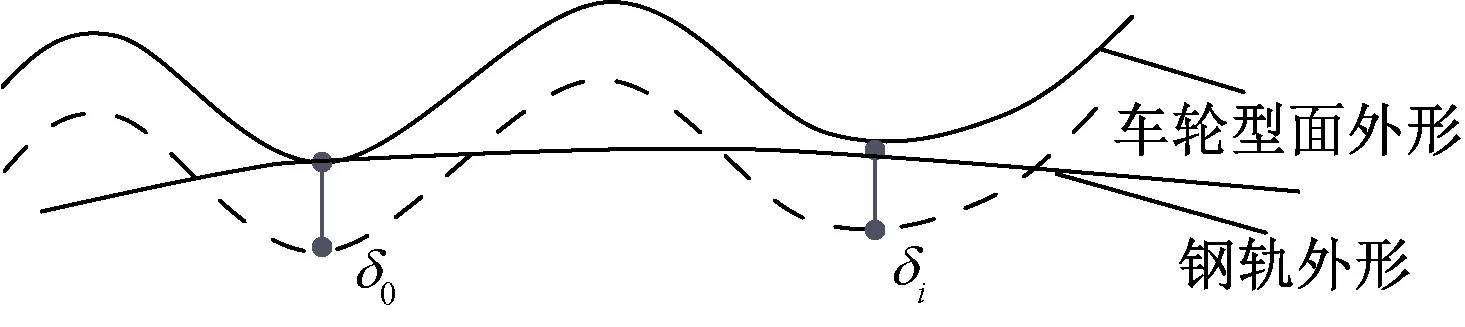
图10 轮轨多点接触示意图

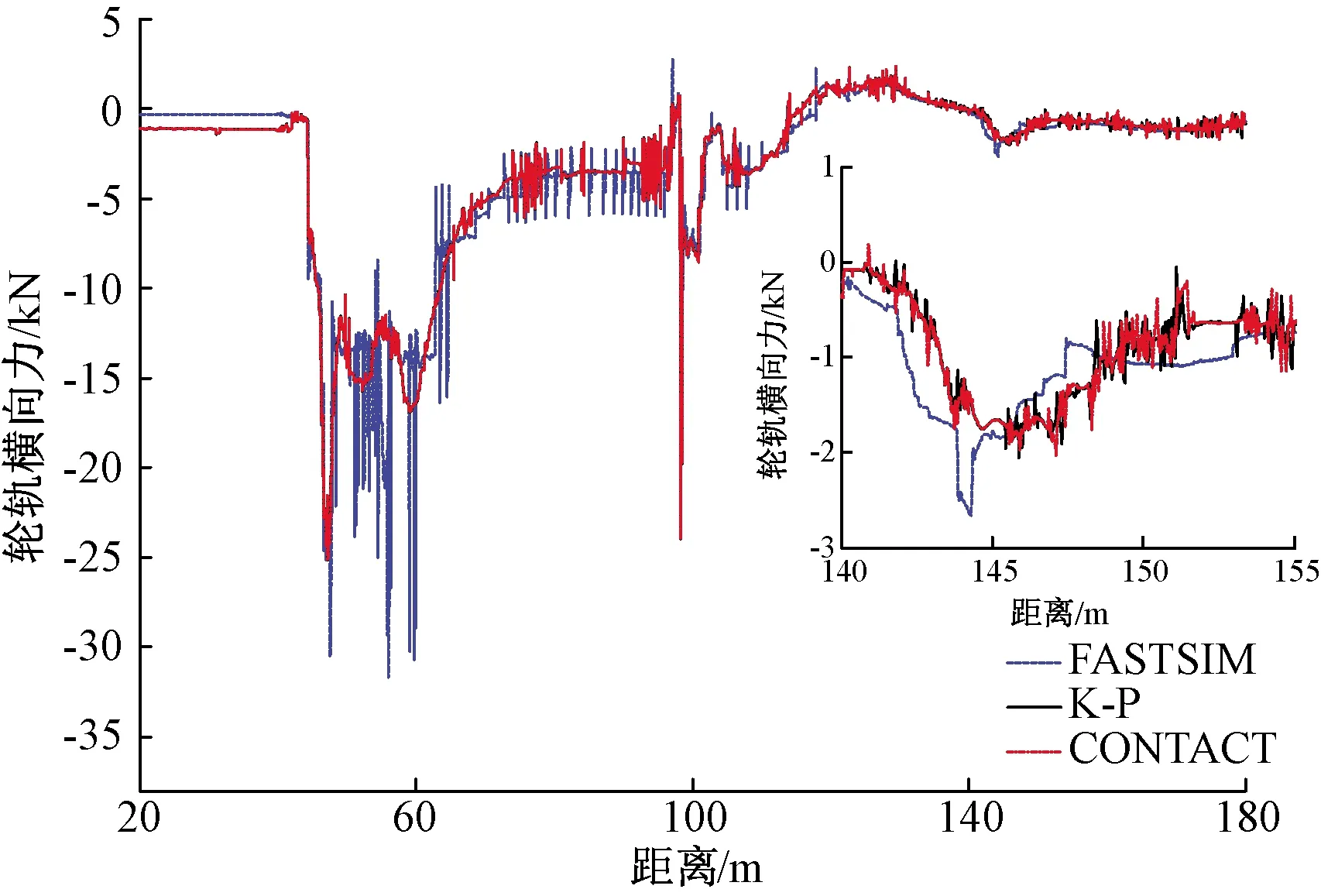
图11 不同轮轨接触理论下轮轨横向力计算结果对比

图12 不同轮轨接触理论下轮轨垂向力计算结果对比

表4 不同轮轨滚动接触计算方法结果比较

3 车辆通过道岔的振动特性分析

为研究车辆通过道岔的振动特性，根据建立的车辆-道岔耦合动力模型，设置60～100 km/h，步长为10 km/h的5个速度等级，以及车辆在不同运行里程下的磨耗型面。应用车辆振动特性分析指标分析磨耗型面对过岔时的振动特性影响。

图13 轮轨力峰值变化情况

3.1 轮岔相互作用

图13(a)为不同速度和磨耗里程型面轮轨横向力的极大值变化情况，轮轨横向力达到最大值时的情况为：车轮通过道岔转辙区；车轮通过尖轨位置。轮轨横向力最大值与速度成正比，且速度提高对轮轨横向力的增长呈现非线性趋势。但是当型面磨耗增大到一定程度时，其轮轨横向力最大值反而会减小。出现这种情况的原因在于当磨耗增大到一定程度时，车轮经过道岔时接触形式会变成多点、共形接触，这种接触形式会改善横向的轮轨匹配特性[12]。例如，车辆在采用无损型面与已运行25万km的型面进行分析时，同样以80 km/h通过岔道，轮对横向力最大值分别为27.43 kN和22.39 kN，下降幅度可达18.37%。图13(b)为轮轨垂向力最大值的变化情况，轮轨垂向力最大值与磨耗深度成正比，磨耗深度越大，轮轨垂向力最大值越大。根据高速列车动力学规范，轮轨垂向力极限值Pmax=170 kN。当磨耗为0.5 mm，车辆以100 km/h的过岔速度运行时，轮轨垂向力峰值为176.87 kN，超出运行允许极限值。

以80 km/h过岔速度分析，图14为轮轨力功率谱密度变化的对数图，在12 Hz后显露出差异，其中15.3万km的功率谱数值最大，说明该里程的磨耗型面产生的轮轨横向力作用最剧烈。轮轨垂向力功率谱密度变化曲线表明，轮轨垂向力频率分布主要为10 Hz以下的低频。对比初始型面的曲线和各磨耗阶段的功率谱曲线不难发现，在大于100 Hz的中高频，随着车轮型面磨耗量增加，功率谱密度值随着运营里程数增大而明显上升。

图14 轮轨力功率谱密度变化情况

3.2 车辆运行安全平稳性

3.2.1 安全性

图15～图17对车辆的脱轨系数、轮重减载率和磨耗功率的峰值变化进行了说明。其中轮轨横向力最大值通常在辙叉区产生，这与脱轨系数表现出的规律大致相同。磨耗量逐渐增加时，脱轨系数整体波动较小。当车辆使用未产生磨耗的车轮以100 km/h的速度通过道岔时，脱轨系数达到最大值0.51。轮重减载率由于作用时间极短(小于0.01 s)，会经常出现超过标准的情况[6]，因此需要对其进行滤波处理。经过20 Hz的低通滤波处理，轮重减载率变化情况如图16所示，车轮型面磨耗量增加后，5条曲线均表现出了减小的趋势，且车辆运行速度越大，减小趋势就越明显。

图15 脱轨系数峰值变化情况

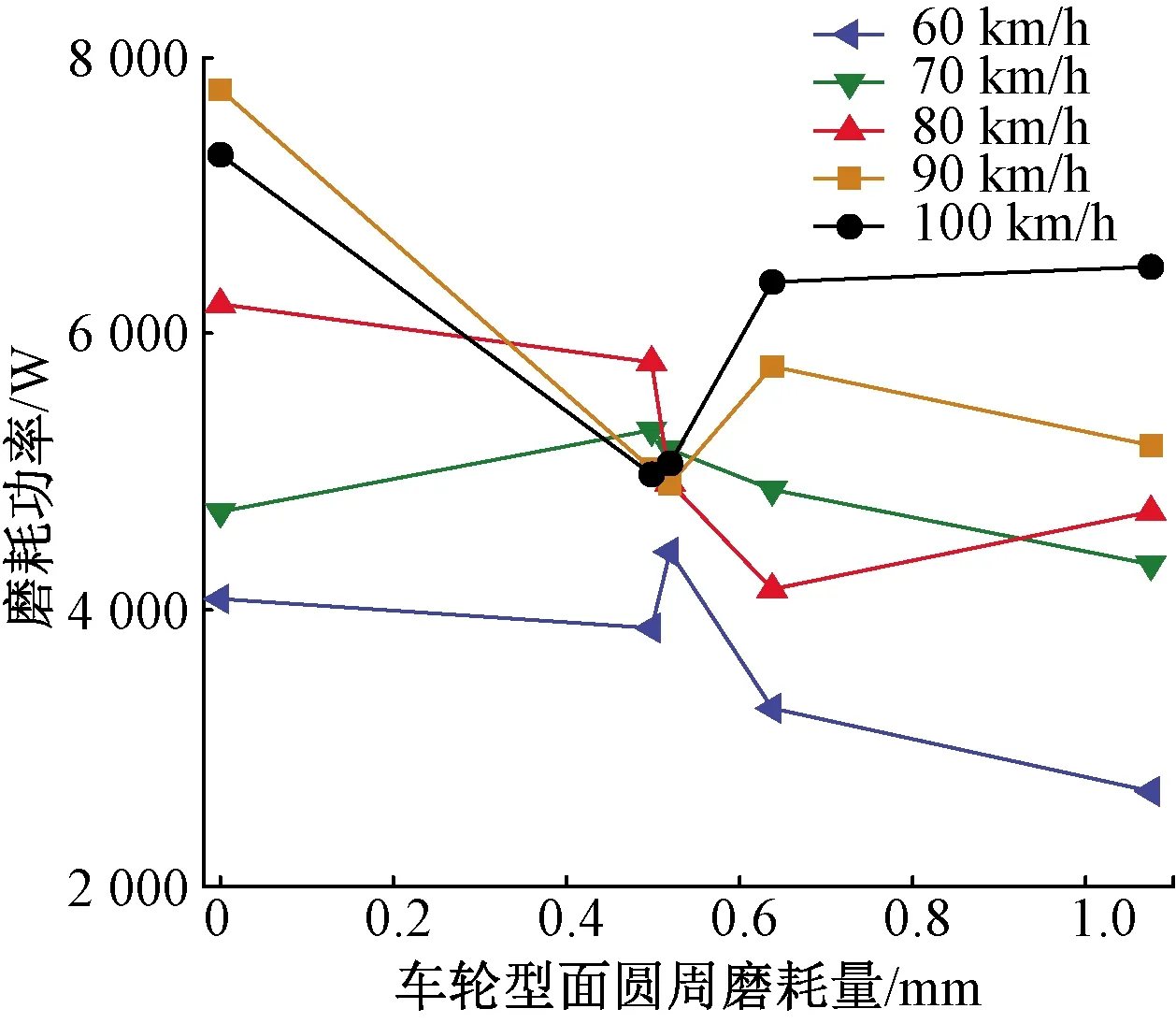
图17 磨耗功率峰值变化情况

利用磨耗功率评价车轮的磨耗性能。

Mwear=|Fx·ξx|+|Fy·ξy|+|Mn·wn|

( 9 )

式中：F为蠕滑力，下标x表示方向为纵向，即纵向蠕滑力；ξ为蠕滑率，下标y表示方向为横向，即横向蠕滑率；Mn为自旋蠕滑力矩；wn为自旋蠕滑率。

从磨耗功率峰值变化情况可知，在磨耗进入一定阶段后(磨耗量0.5 mm左右)，无论哪个速度等级，轮轨磨耗功率会达到约5 kW的一个相对稳定的数值，其后峰值会随着速度等级不同继续增大或者减小[12]。

3.2.2 平稳性

(1)车体振动特性

图18、图19为车辆以80 km/h标准过岔速度通过时的车体横向和垂向加速度功率谱密度对数变化图。从图中可以看出，随着运营里程数增加，车体横向加速度功率谱密度曲线波动情况并不明显。车体横向振动加速度主频为1.4 Hz，垂向振动加速度主频为0.8 Hz。垂向加速度功率谱曲线整体幅值上升。由于道岔结构不平顺主要表现为短波，主要引起轮轨间的高频冲击力，而车体加速度主要受长波轨道不平顺的影响较大，因此对车体垂横向加速度的影响较小。

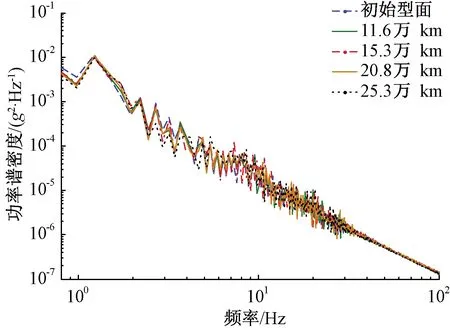
图18 车体横向加速度功率谱变化情况

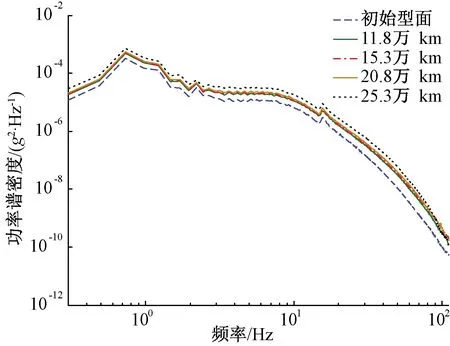
图19 车体垂向加速度功率谱变化情况

Sperling指标通常作为衡量车辆乘坐舒适性和运行品质的指标。Sperling指标变化情况如图20、图21所示，其中横向Sperling指标随着磨耗量增加无明显变动，最大值为100 km/h过岔速度时，达到2.16。说明横向Sperling指标主要对速度变化敏感。垂向Sperling指标随着磨耗量累积逐渐上升。说明车轮型面的磨耗会影响列车乘坐舒适性，尤其对垂直方向舒适度影响明显。车轮初始型面在80 km/h过岔速度条件下，垂向Sperling指标为1.07，运行25.3万km后，指标的最大值达到1.15。横垂向的Sperling指标在5种速度等级下均小于安全限度值2.5，表明车轮磨耗对乘坐舒适度的影响在可接受规范内。

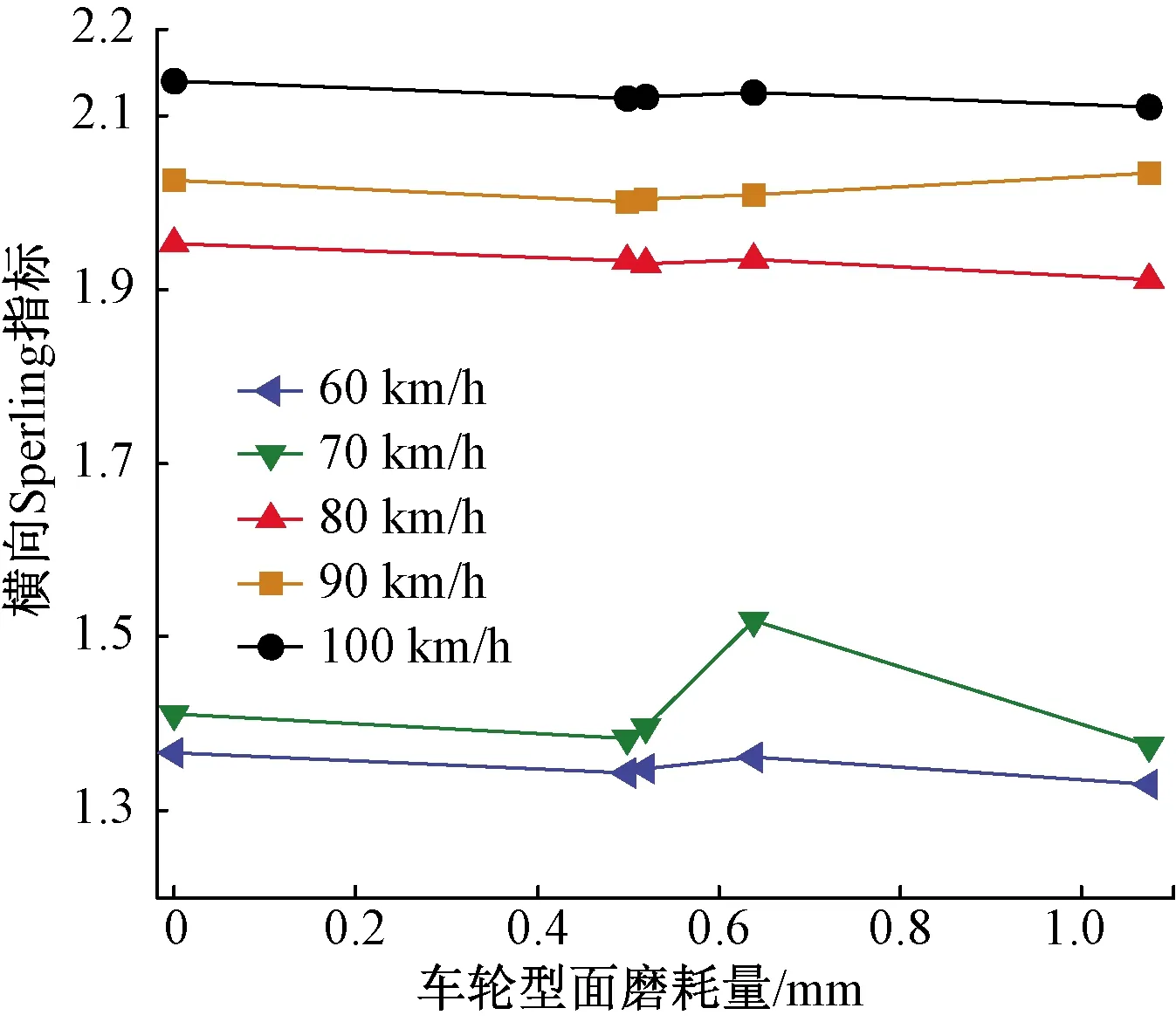
图20 车体横向Sperling指标变化情况

图21 车体垂向Sperling指标变化情况

(2)构架振动特性

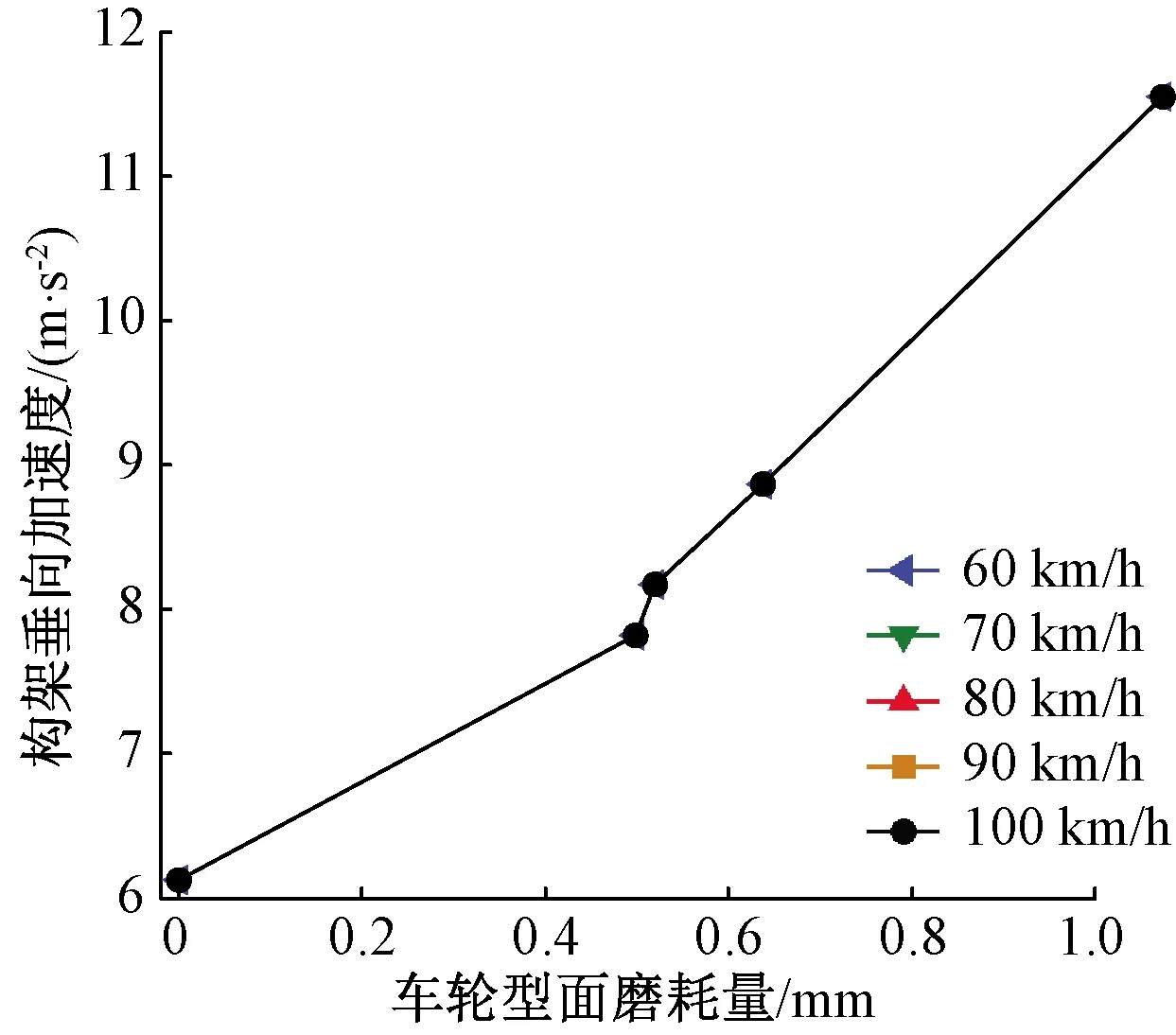
图22 构架垂向振动加速度峰值变化情况

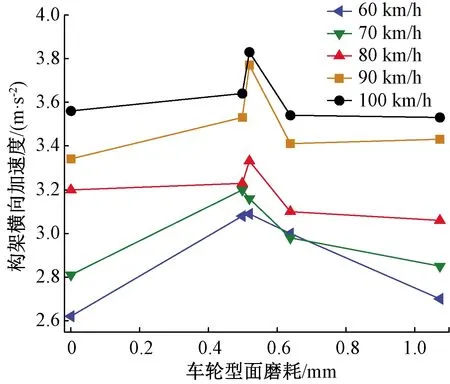
图23 构架横向振动加速度峰值变化情况

图22、图23分别是车辆构架垂向和横向振动加速度峰值变化图，从图中可以看出，构架的垂向加速度峰值基本不随速度变化而波动，5种速度下的峰值曲线基本重合。车轮凹形磨耗对构架垂向振动加速度峰值影响较为突出，随着磨耗的恶化，加速度峰值出现明显增长，从初始型面的6.15 m/s2增大到11.6 m/s2，提高了88.61%。构架横向振动加速度峰值先小幅度上升，再下降回归，运营25.3万km下的横向振动加速度值和初始无磨耗型面振动数值相似。构架横向振动加速度峰值最大可达3.83 m/s2。

(3)轮对振动特性

图24、图25为轮对加速度峰值变化图。轮对垂向振动加速度和构架垂向加速度变化规律相似，在车轮磨耗量小于0.5 mm的阶段，轮对的垂向最大加速度值保持稳定，基本没有变化。但是当磨耗量超过0.5 mm后，轮对的垂向最大加速度值变化幅度较大，加速度最大值由64 m/s2增大到102 m/s2。当车轮磨耗量从0增加到0.5 mm时，横向振动加速度最大值会逐渐减小，车轮磨耗量为0.5～0.6 mm时，横向振动加速度最大值会有小幅度变化。总体看来，轮对横向振动加速度峰值会随着磨耗量增加略有降低。

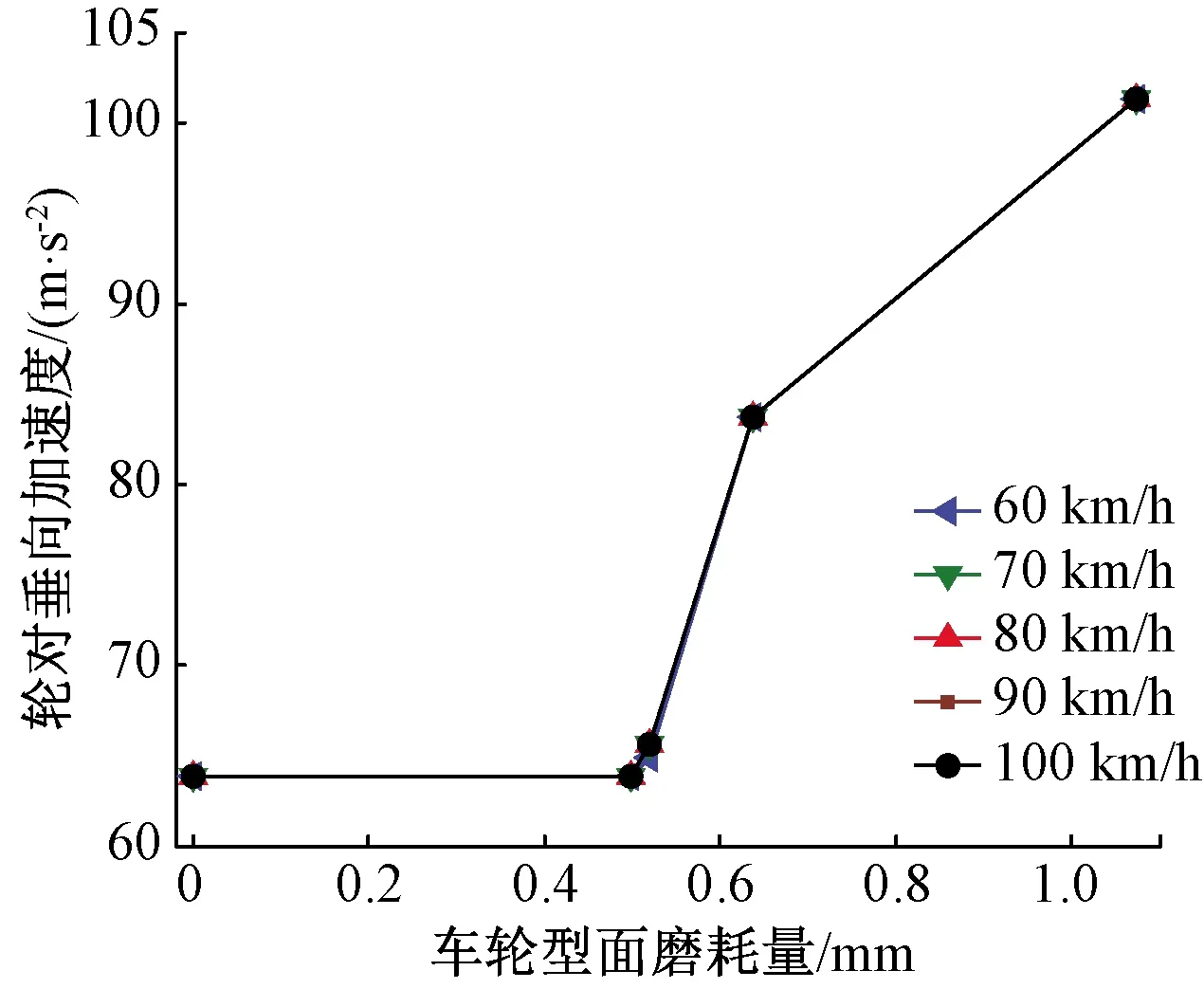
图24 轮对垂向最大振动加速度变化情况

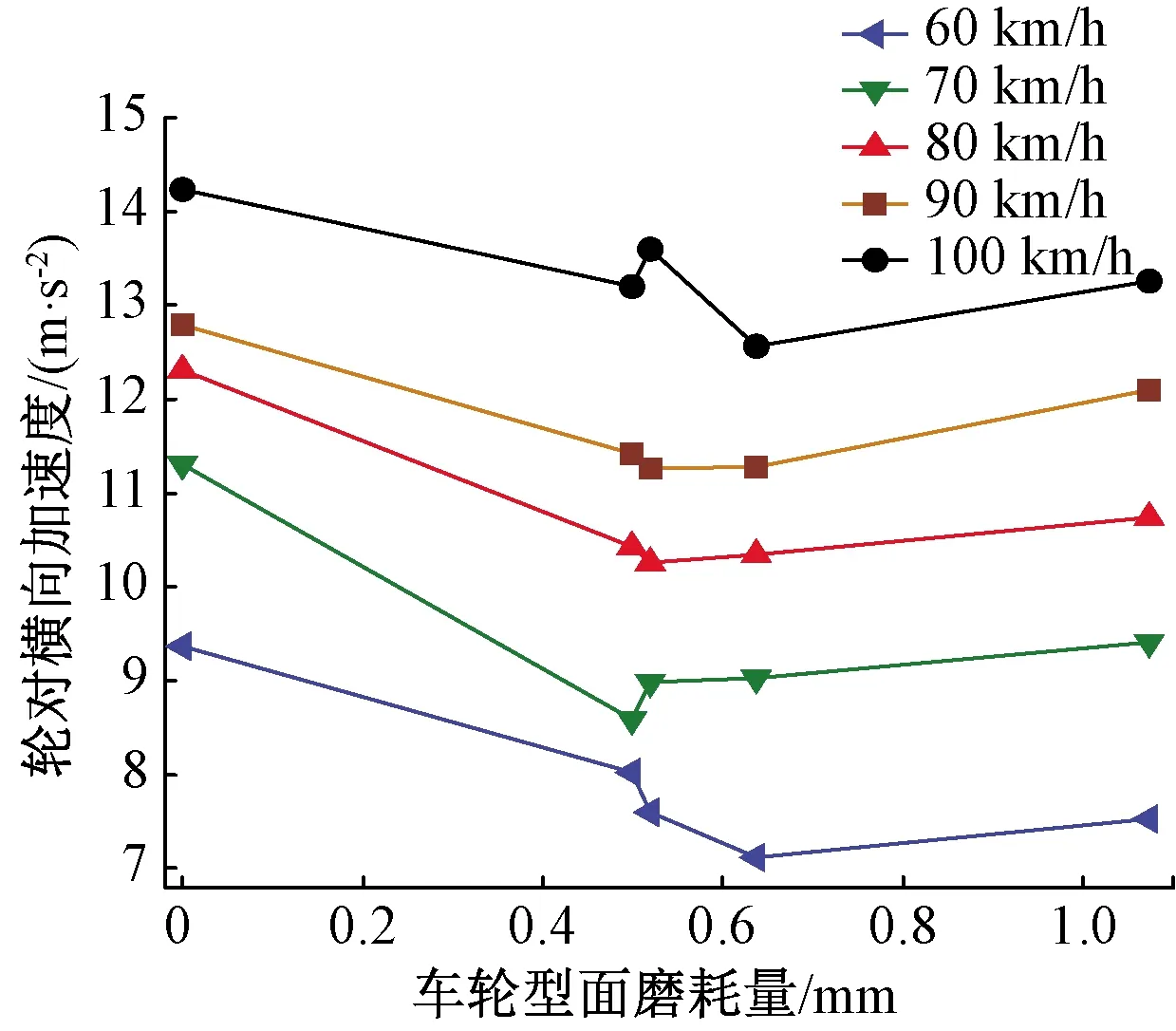
图25 轮对横向最大振动加速度变化情况

3.3 道岔振动特性分析

图26、图27所示为钢轨振动位移峰值变化情况，车轮型面磨耗量相同的情况下，列车通过道岔速度越大，钢轨的横、垂向振动位移峰值越大；在列车通过道岔速度相同的情况下，车轮型面磨耗量增大的过程中，横向振动位移峰值逐渐减小但垂向振动位移峰值有先减小后增大的趋势。

图26 钢轨垂向振动位移峰值变化情况

图27 钢轨横向振动位移峰值变化情况

4 结论

(1)车轮型面磨耗量与轮轨垂向力大小成正比，与轮轨横向力成反比。

(2)磨耗功率在列车不同运营里程内变化，会统一达到一个相对稳定数值5 kW左右。车体振动加速度、Sperling指标、构架和轮对振动加速度，均在垂向方向对车轮型面磨耗较敏感，但横向方向变化相对较小。

(3)道岔区域钢轨的各方向振动位移峰值与车轮型面磨耗的关系差异较大，其中横向联系较为紧密，垂向影响较小。

(4)对道岔尖轨、心轨等关键部位进行设计时，需重点考虑不同运营里程下的车轮磨耗型面带来的影响，以提升列车运行品质。