铁路圆端空心墩等效塑性铰长度试验研究

邵长江，漆启明，韦 旺，肖正豪，肖来川，王 猛

(1.西南交通大学 土木工程学院，四川 成都 610031；2.西南交通大学 陆地交通地质灾害防治技术国家工程实验室，四川 成都 610031)

强震作用下，混凝土构件在塑性变形较为集中的区域会形成塑性铰，该塑性区域长度与构件的整体变形具有一定联系。为简化桥梁抗震设计中墩顶位移的估算，文献[1]定义了桥墩的等效塑性铰长度，假定该长度范围内的塑性曲率为常数，通过墩高、屈服曲率和极限曲率计算桥墩的塑性转动能力及极限容许位移。塑性铰力学特性及等效塑性铰长度是桥梁抗震延性分析理论和设计方法的重要内容，因而等效塑性铰长度计算方法成为大量文献[1-15]的研究热点，相关研究成果已被Eurocode8[16]、Caltrans[17]、AASHTO[18]、NZS3101[19]、JRA[20]以及JTG/T B02-01—2008《公路桥梁抗震设计细则》[21](以下简称《细则》)和CJJ 166—2011《城市桥梁抗震设计规范》(以下简称《城规》)[22]等规范采纳。

目前，国内外学者研究成果主要涉及方形/矩形、圆形截面梁或墩柱[1-13]，仅有少数成果涉及铁路圆端形桥墩的研究[14-15]，但并未对铁路圆端空心墩延性能力估算的合理性、准确性进行深入分析及验证[23]。文献[2-3]通过测试极限曲率和位移，分别提出了混凝土梁的塑性铰长度计算模型以预测其极限变形能力。文献[4-5]分别在考虑剪切效应和尺寸效应基础上，研究了矩形截面悬臂梁塑性铰长度的变化规律，这种构件在本质上与无轴压墩柱相同。文献[6-7]分析了轴压对方形截面墩塑性铰的影响，认为塑性区域范围会随着轴压的增加而扩大。文献[8-9]提出了圆形截面桥墩塑性铰长度的计算公式。文献[10]基于1 000多个梁、柱及剪力墙试验，建议了塑性铰长度的估算公式。而文献[1,11-12]基于实心和空心墩柱，回归出适用于两者的塑性铰长度表达式。文献[13]关于文献[1]的修正模型已被多个桥梁抗震规范[17-18,21-22]采用。毋庸置疑，上述成果为混凝土梁、圆形及方形/矩形截面墩的延性设计提供了重要的理论支撑。但鉴于圆端空心墩在截面形状、约束混凝土效应方面的特殊性，其地震损伤机制可能不同于其他截面墩柱，延性性能也会在相当程度上异于实心墩，直接套用已有成果进行圆端空心墩的抗震设计，缺少理论依据和试验验证。

因此，本文以单线铁路圆端空心墩为研究对象，通过4个缩尺试件的拟静力试验，观察加载过程中桥墩塑性铰区域的形成及扩展，测试墩身曲率分布，探讨桥墩的塑性铰特性。在此基础上，将采用各种规范及相关学者的塑性铰长度公式计算的结果与试验值进行比较，给出圆端空心墩的等效塑性铰长度建议公式，为此类桥墩的延性抗震设计提供参考。

1 试验概况

1.1 模型设计

原型墩高30 m，墩底实心段高1.5 m，倒角尺寸0.5 m×1 m，空心墩身外壁坡度为40∶1，内壁坡度70∶1，墩底倒角上缘(即控制截面)的纵筋率和配箍率分别为0.971%和0.737%。根据相似理论取1∶6进行缩尺设计，模型尺寸及配筋见图1。模型墩高5 m，墩底实心段高度25 cm，倒角尺寸为8.5 cm×17 cm。墩底控制截面壁厚为11.3 cm，墩顶倒角下缘处壁厚7.4 cm。为保证应变和应力相似常数为1，模型材料与原型一致，墩身采用C35混凝土浇筑，采用直径12 mm的HRB400纵筋、直径6 mm的HPB300箍筋。结合GB 50111—2006《铁路工程抗震规范》[24]，模型配箍率分别为0.325%、0.910%和1.510%，以研究箍筋用量对塑性演化的影响；考虑地震下控制截面动轴力，轴压比取0.10和0.15，桥墩主要设计参数如表1所示。

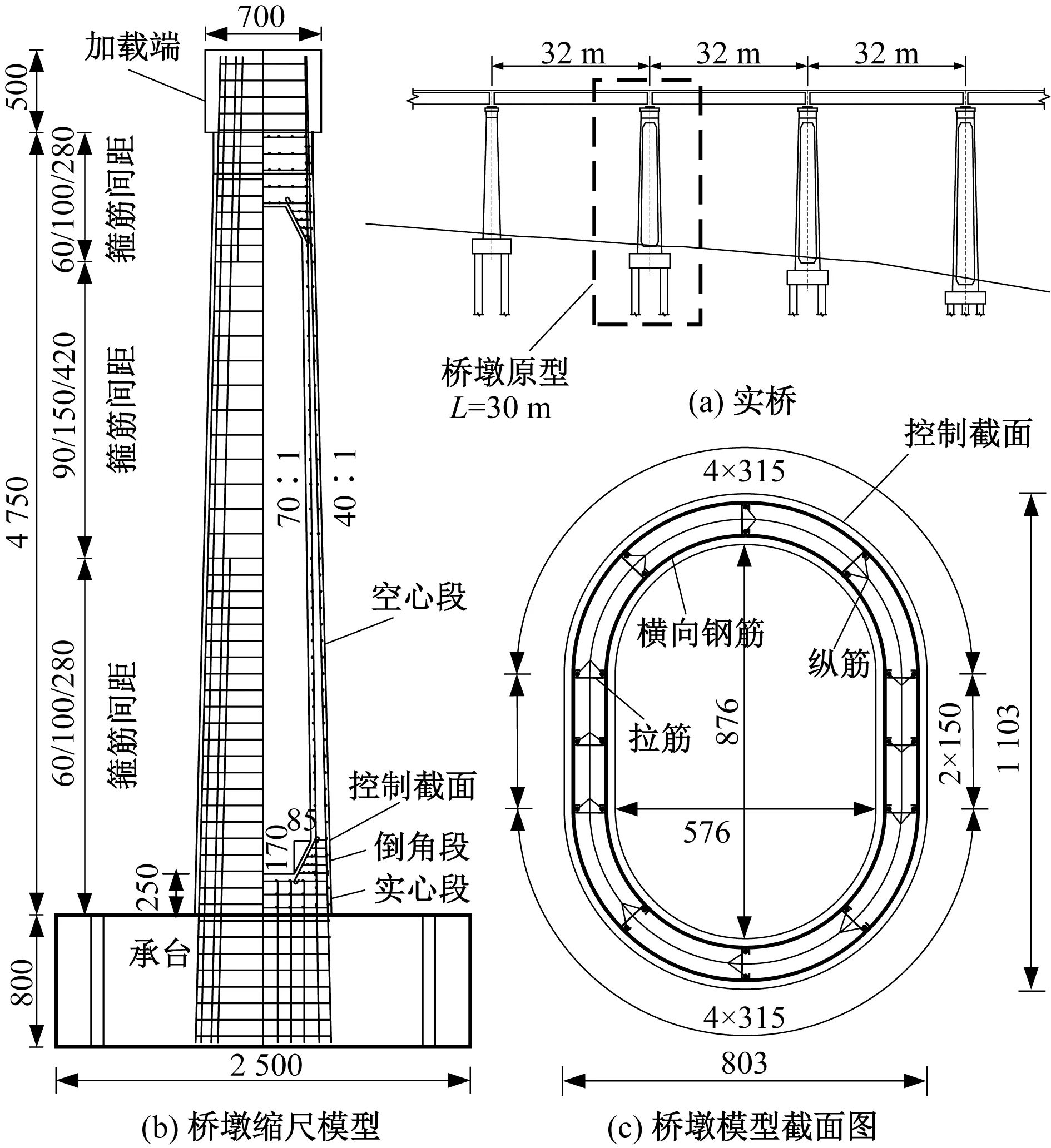
图1 桥墩尺寸及配筋(单位：mm)

表1 桥墩试件参数

1.2 加载装置及测试内容

试验在西南交通大学陆地交通地质灾害防治技术国家工程实验室进行。试验加载制度见图2，采用力-位移混合加载模式[25]。竖向采用3 000 kN液压千斤顶施加轴力，通过MTS 1 000 kN高性能全动态作动器施加往复循环水平荷载，加载系统和仪器布置见图3。试验测试内容包括墩顶位移、荷载及墩底区域的塑性变形，其中，墩顶荷载和位移由作动器获得，墩身位移由激光位移计获取。墩底曲率是测试的重点，需要通过墩底竖向位移反算，各测点与承台顶面的距离分别为40、80、120、160 cm，试验曲率的计算方法参考文献[26]。鉴于桥墩纵桥向更易破坏，因此试验沿弱轴方向(纵桥向)加载。为便于数据分析，规定作动器施加推力为正向加载，拉力为反向加载；墩身的作动器一侧为东(E)侧，对面一侧为西(W)侧。

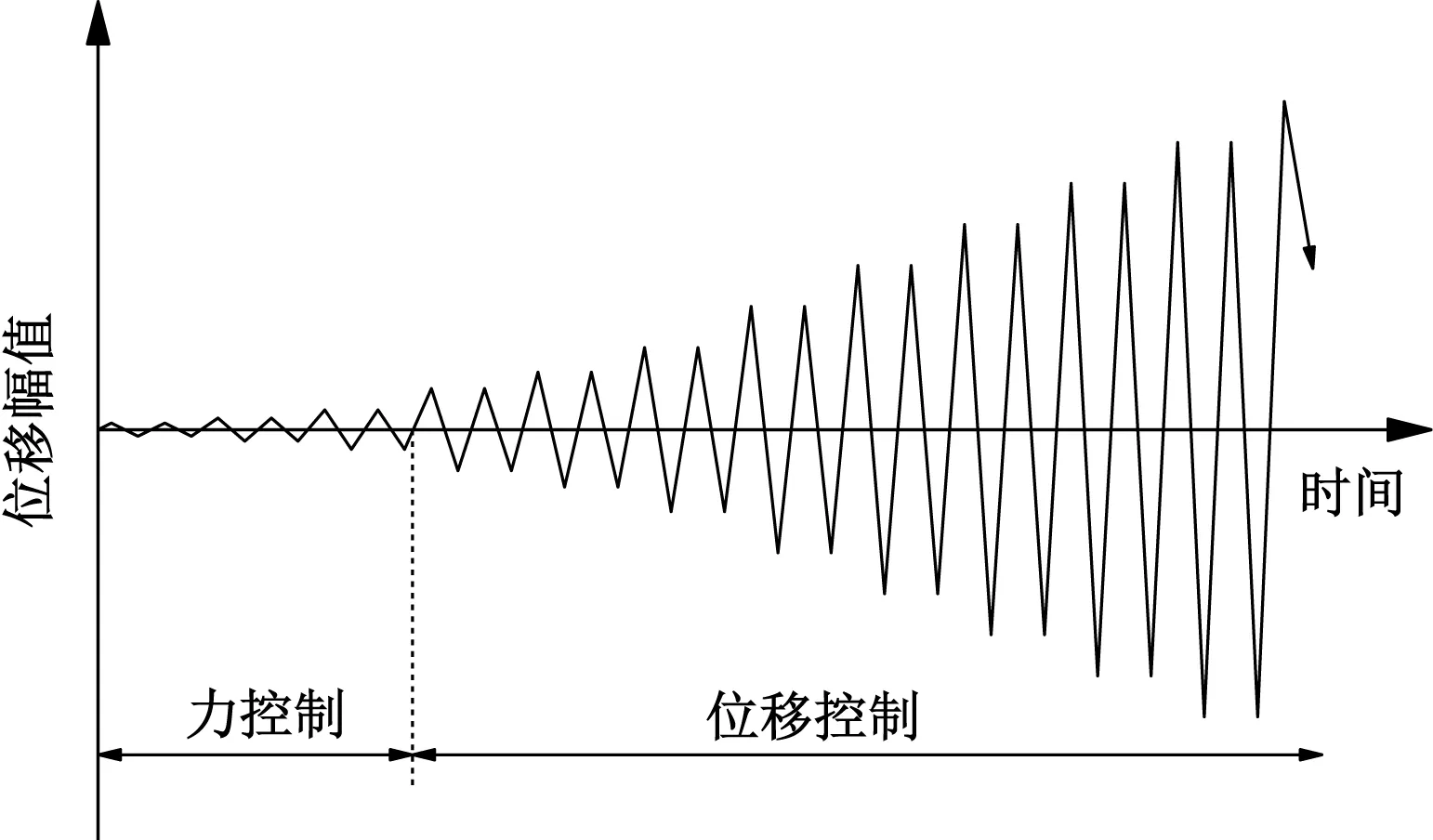
图2 加载制度

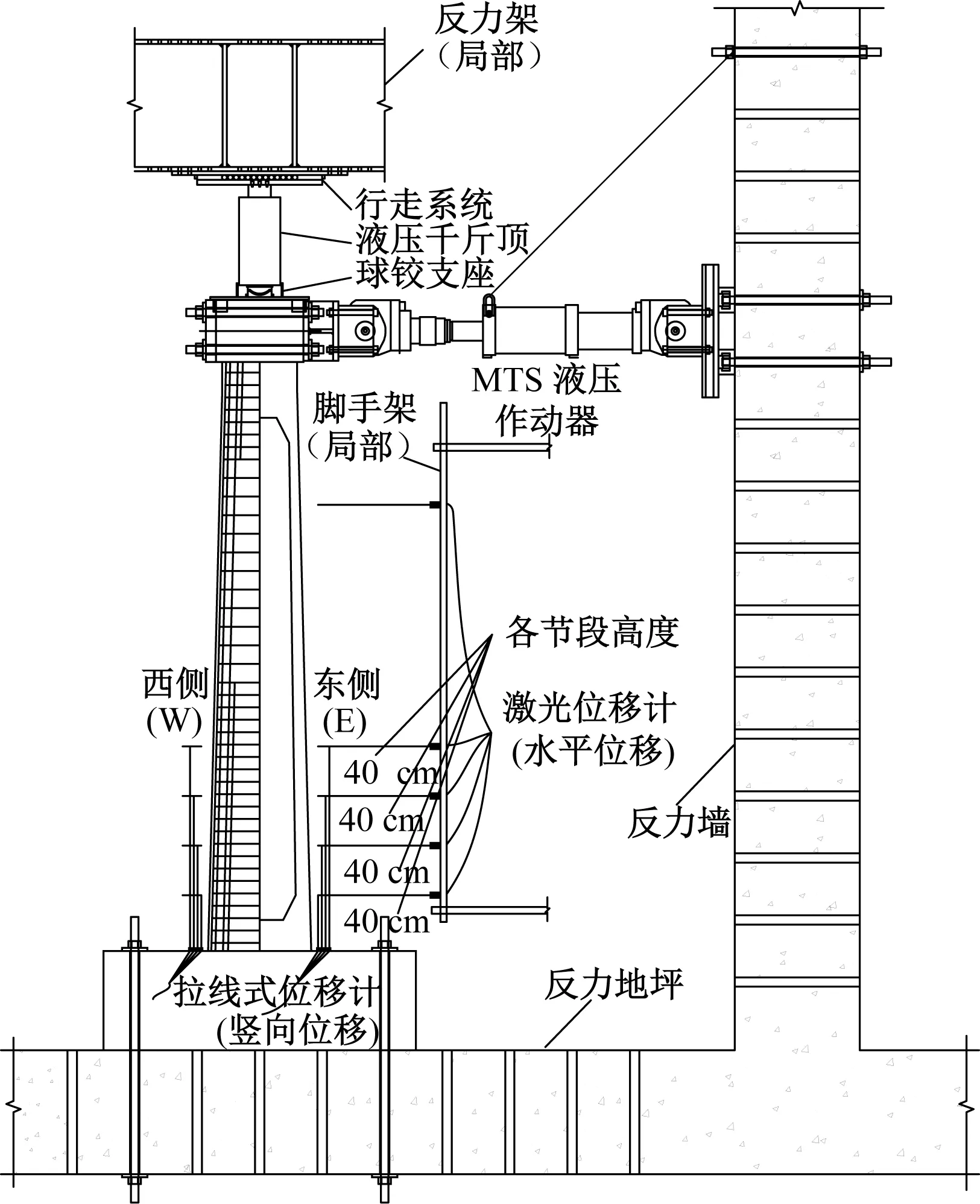
图3 加载装置及仪器布置

2 试验结果分析

2.1 开裂损伤行为描述

总体而言，4个试件均发生弯曲破坏，并按预期形成了塑性铰，以塑性演化最典型的试件S2为代表，简述其破坏历程及最终破坏形态，见图4。

图4 试件S2损伤历程及最终破坏形态

在力控制阶段，施加水平推力100 kN时，墩底根部实心段出现极其微小的裂缝，即图4(a)中A1区域裂缝。墩顶荷载为142 kN时，墩身E侧距墩底约45 cm的空心段倒角处首次出现明显的弯曲裂缝，即图4(a)中A2区域两条较长的弯曲裂缝；在W侧几乎相同的高度也出现了弯曲裂缝，说明该处是墩身最不利截面。墩顶位移达到25 mm时，原有弯曲裂缝继续发展，在距墩底45～150 cm的范围内墩身正反两侧出现3条新的弯曲裂缝(图4(a))，由钢筋应变可知最外层纵向钢筋已屈服。当位移为48 mm时(图4(b))，墩身空心段范围出现较多弯曲裂缝，已有裂缝宽度扩大，部分水平裂缝延伸至侧面变成斜裂缝。加载位移为72 mm时，新出现的水平裂缝数量相对较少，特点是弯曲裂缝宽度的扩大和斜裂缝的延伸，塑性区域初步形成。

墩顶位移达到96 mm时(图4(c))，桥墩正反面均新出现了部分弯曲裂缝，受拉侧已有弯曲裂缝及所延伸形成的斜裂缝宽度显著增大，斜裂缝相交形成网格状。当工况为120 mm时，桥墩受压时距墩底40～70 cm范围内出现局部“起皮”现象，局部区域硬骨料发生脱落，已有弯曲裂缝开始衍生出竖向和斜向细小裂缝，侧面斜裂缝交错形成密集网格状，且桥墩颈部出现些许竖向裂缝(图4(d))；同时，正向达到最大承载力256.0 kN，反向达到最大承载力284 kN。位移为144 mm时，塑性铰区非线性变形进一步加剧，弯曲裂缝及斜裂缝宽度持续增大，受压侧(E侧)局部出现混凝土块状剥落，承载力开始下降。施加168 mm位移时，E侧墩底倒角处裂缝明显宽于其他裂缝，钢筋与混凝土之间相对滑移现象显著，W侧墩底有骨料脱落，承载力下降至峰值的95.8%；反向施加168 mm位移时，墩底受压侧出现大面积混凝土保护层压溃和剥落、纵筋裸露及屈曲，此时桥墩承载力急剧下降至峰值荷载的44.1%，见图4(e)，试验停止。其余试件破坏历程类似，不再赘述。

图5为桥墩模型S2的滞回曲线和骨架曲线，其滞回曲线较为饱满，说明按规范设计的此类桥墩能形成预期的塑性铰，具有较好的塑性耗能能力。

2.2 墩身平均曲率

根据所测墩身竖向位移可以计算得到各节段平均曲率，见图6。随着墩顶位移的不断增加，墩身各节段区域的平均曲率也随之增大。但是，墩身曲率分布与等截面实心墩存在显著差异[1]，墩底倒角所在的区域2处平均曲率φ2明显大于区域1处平均曲率φ1。而随着截面高度的增加，在区域3处的平均曲率φ3与φ2相比急剧减小，区域4处曲率φ4略小于φ3，由此可知除区域2外墩身其余部分塑性程度相对较低，与2.1节试验现象和观测结果一致。

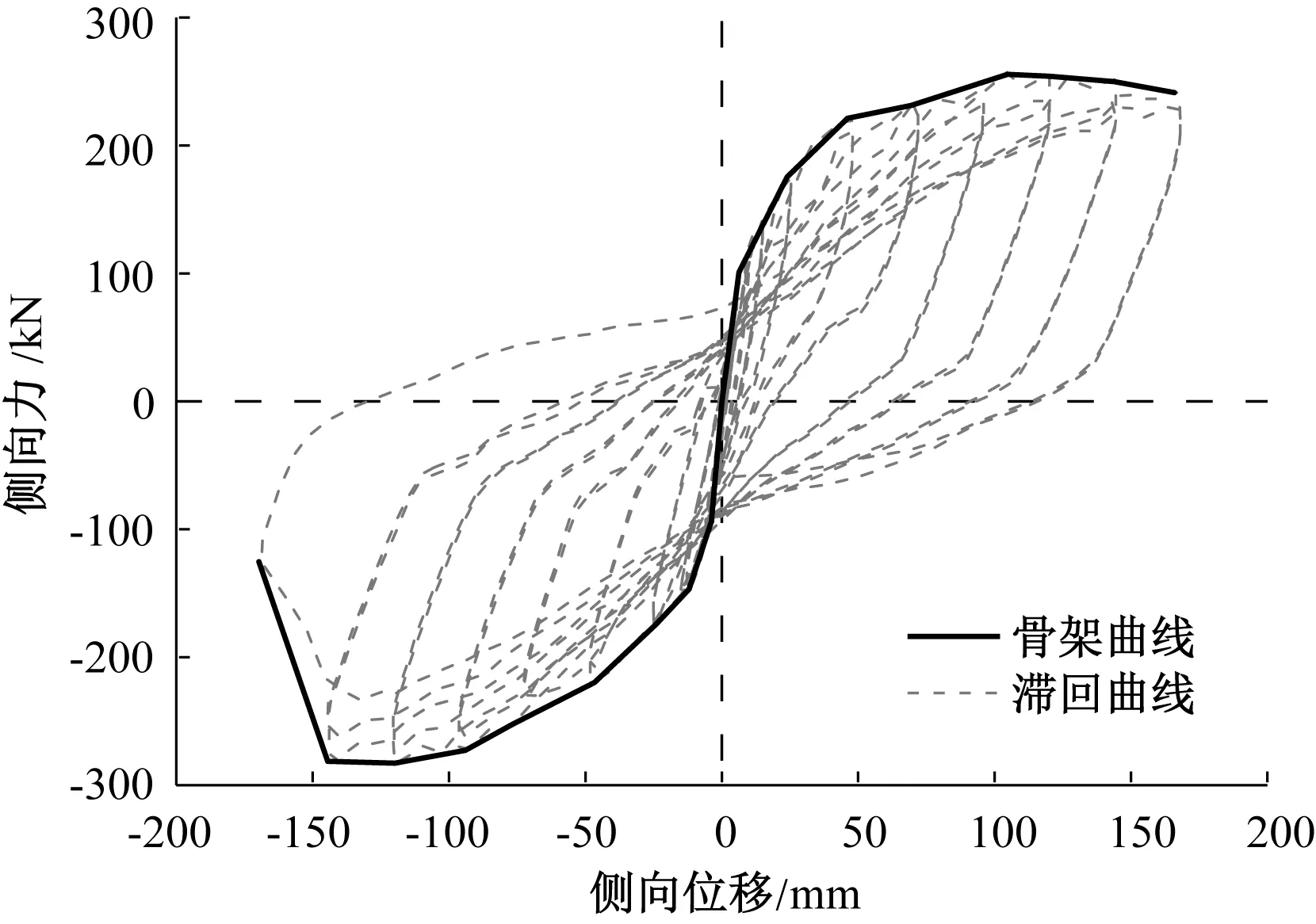
图5 试件S2滞回与骨架曲线

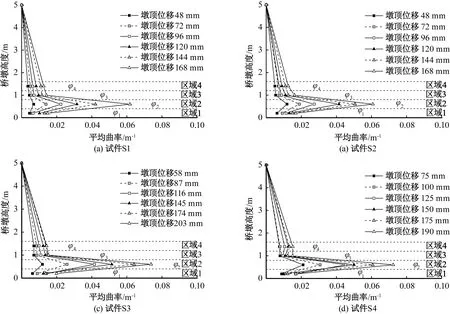
图6 各试件平均曲率分布

2.3 损伤机制分析

为阐明圆端空心墩试件开裂行为、塑性铰机制及曲率分布特性，给出了试件初始弹性状态下的归一化弯矩M、截面抗弯模量W和无量纲应力M/W沿墩身分布情况，见图7。抗弯模量W体现了墩身各截面抵抗弯矩的能力，可根据截面特性计算；利用归一化M和W相比所得的无量纲应力可以整体比较桥墩开裂前各截面的应力水平。由于墩底和墩顶实心段、倒角过渡段及空心墩身变截面影响，抗弯模量W沿墩身变化较大，弯矩M呈线性变化，因而无量纲应力M/W相对同类型等截面桥墩应力M/W′更大，墩底倒角上缘(控制截面)理论上为桥墩最不利受力位置。

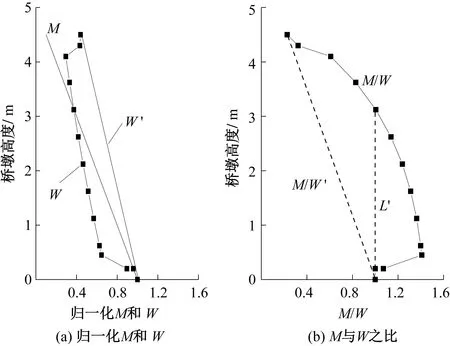
图7 墩身归一化弯矩M、抗弯模量W和无量纲应力分布

图8给出了各试件发生首次屈服位移工况及最大位移工况下的裂缝分布。与理论分析相近，第一条明显弯曲裂缝C1出现在控制截面附近；与此同时，该区域理论压应力也最大，最大位移工况下混凝土保护层的压溃剥落、纵向钢筋的屈曲断裂均发生在墩底空心段及墩底倒角附近。因此桥墩塑性变形集中在墩底倒角及附近空心段，塑性铰相对普通等截面实心墩整体上移，故区域2平均曲率φ2最大。空心段截面刚度EI0的变化使得墩底倒角以上一定区域(长度为L′)内的理论M/W也较大，导致桥墩最终裂缝分布也主要集中在该范围内，约占墩身高度的2/3。为防止强震下墩底塑性铰区发生剪切破坏，应尤为注意空心墩底部倒角处的构造细节。根据试验，体积配箍率0.910%时圆端空心墩具有较好的延性性能。

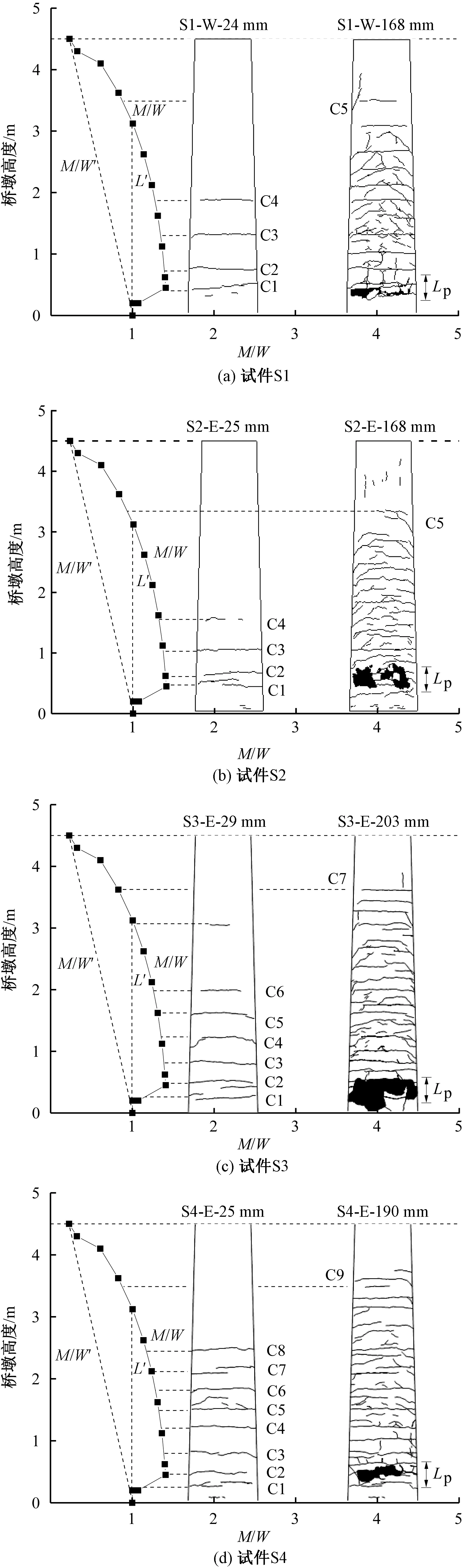
图8 无量纲应力分布与墩身裂缝的关系

3 等效塑性铰长度评估

3.1 实测等效塑性铰长度

塑性铰长度(Lp)的概念最早源于钢筋混凝土梁塑性区域的弯曲转动能力评估[2]，文献[27]则将塑性铰长度的定义推广至悬臂梁，而文献[1]将塑性铰长度应用于桥墩。

基于试验观测的塑性区域长度通常具有主观性，往往需要根据实测位移和曲率反算，从而准确量化塑性铰长度Lp。文献[27]中给出了等截面实心墩柱的等效塑性铰简化模型，见图9(a)，假定Lp范围内的塑性曲率为常数，此时由式( 1 )可以确定桥墩容许位移。将式( 1 )变换为式( 2 )，即可利用试验所测位移和曲率计算桥墩等效塑性铰长度试验值。

( 1 )

( 2 )

式中：δu为墩顶的极限位移；δy为墩顶的屈服位移；δp为墩顶的塑性位移；L为桥墩计算高度；φy、φu分别为屈服曲率和极限曲率。

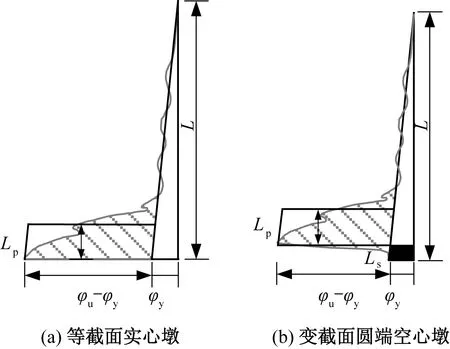
图9 等效塑性铰长度定义

鉴于铁路圆端空心墩在塑性行为及曲率分布上与等截面实心墩存在较大差异，不能直接套用式( 2 )计算Lp的实测值，故根据墩身曲率分布将原简化模型修正，见图9(b)，此时由式( 3 )计算圆端空心墩容许位移，由式( 4 )计算圆端空心墩等效塑性铰长度实测值。

( 3 )

( 4 )

式中：Ls为桥墩墩底实心段高度。

根据铁路抗震规范[24]，将最外层纵筋屈服时对应的墩顶位移作为屈服位移，同时将承载力下降至峰值承载力的80%时的位移作为容许位移，结合实测曲率与位移，计算等效塑性铰长度，如表2所示。

3.2 已有模型计算结果

为了克服试验观测的局限性，便于延性抗震设计，大量学者基于试验和理论研究得到了多种塑性铰长度公式。为便于成果梳理，根据试验构件类型和截面形式将部分代表性的模型分为以下四类：(1)方形/矩形实心截面混凝土构件[6]；(2)圆形实心截面墩[8-9]；(3)实心圆形、矩形(方形)截面墩[16,20-21]；(4)空心/实心矩形(方形)、圆形截面墩[10-13]，如表3所示。

表2 桥墩等效塑性铰长度

表3 等效塑性铰长度计算公式

3.3 比较分析

用表3中公式计算4个桥墩模型的等效塑性铰长度，考虑到圆端空心墩底部实心段变形较小，各公式桥墩计算高度扣除了墩底实心段高度。各模型塑性铰长度计算结果与实测值的比较见图10，两者比值的平均值和变异系数如表4所示。分析可知，各模型塑性铰长度计算值介于200 ～650 mm，将实测值包含在内，说明由于各公式回归时所用构件类型、设计参数、加载方式等不同，加之各模型中因素取舍不一，不同公式计算结果存在较大差异。文献[10]公式计算值远大于试验值，可能会高估桥墩的极限容许变形能力；而其余大多数模型预测值均在不同程度上小于试验值，表明相对一般等截面实心墩，变截面圆端空心墩塑性铰区域在上移的同时，其塑性演化范围也在增大[23]。文献[6]公式计算结果最为保守，其可能的原因是该模型的推导源于高轴压比(0.2和0.5)及高配筋率(ρl为1.25%)的实心截面，而文中铁路圆端空心墩模型的轴压比和纵筋率相对较小，使得等效塑性铰长度计算值始终为0.25h。综合来看，文献[16]同时考虑了桥墩高度及应变渗透效应，计算结果略微保守(计算值与试验值比值的平均值为0.96)，从抗震安全性和经济合理性出发可用于单线铁路圆端空心墩等效塑性铰长度的估算。

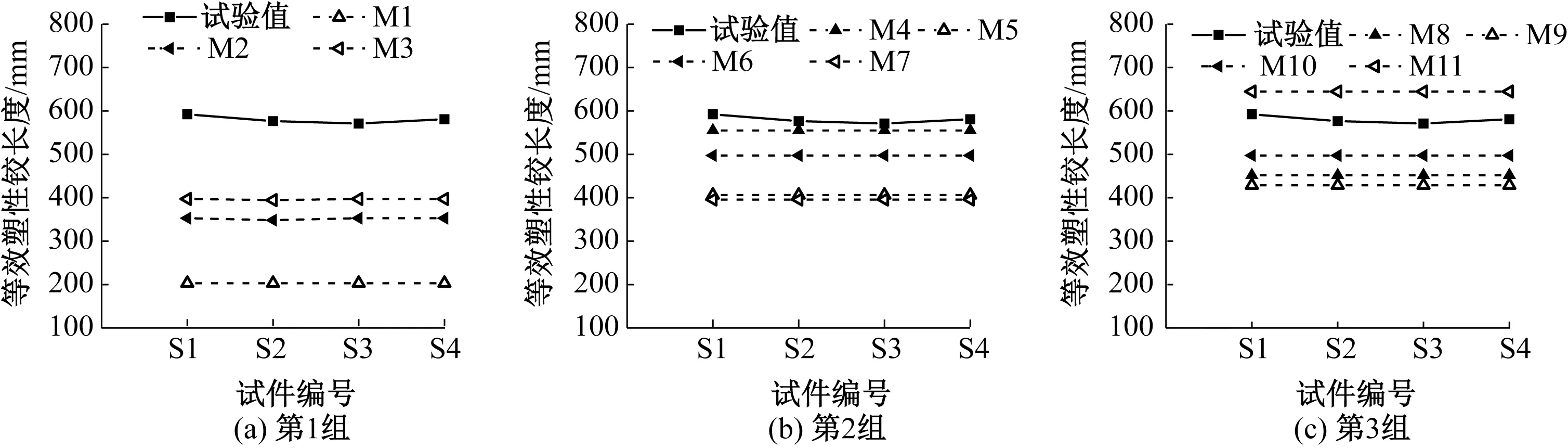
图10 等效塑性铰长度计算值与试验值比较

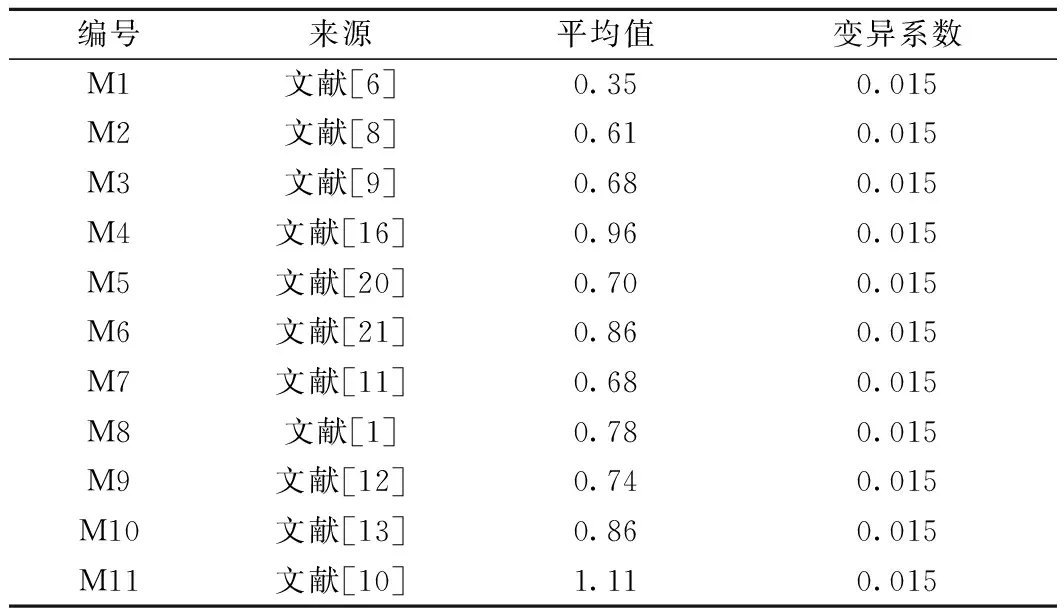
表4 等效塑性铰长度计算值与试验值比值的平均值和变异系数

4 结论

基于4个单线铁路圆端空心墩拟静力试验结果，观测了桥墩损伤历程，分析了裂缝和曲率分布特点，研究了塑性铰特性及演化机制，并探讨了已有公式对圆端空心墩等效塑性铰长度计算的适用性，结论如下：

(1)试验构件均发生弯曲破坏，出现了混凝土的压溃剥落及箍筋屈曲断裂等现象，桥墩下部空心段倒角处出现明显的塑性铰区，同时滞回曲线较为饱满，说明按现行规范设计的圆端空心墩具有较好的塑性变形和耗能性能。

(2)由于墩底实心段、倒角过渡段和空心段变截面的影响，桥墩底部实心段裂缝较少，塑性程度不显著，而墩底变截面段及空心段由混凝土受压、裂缝开裂及纵筋滑移等所引起的曲率变化较大，塑性程度较高，由此导致墩底塑性铰区范围扩大且整体上移。

(3)Eurocode8模型能够较好地评估铁路单线圆端空心墩的塑性铰长度，从抗震设计安全、经济的角度出发，可以用于铁路圆端空心墩的抗震设计。

(4)其余模型对圆端空心墩的等效塑性铰长度计算值差异较大，这些模型均源自力和塑性铰与圆端空心墩差异显著的其他桥墩，因此其对圆瑞空心墩的适用性需审慎对待。

(5)限于试验条件及试件数量，现有研究成果尚不足以全面揭示圆端空心墩的塑性机制，其等效塑性铰长度计算模型亦有待进一步的理论和试验研究。