异构变分辨成像的旋转与尺度特性研究

曹 杰，唐鸣元，肖宇晴，郝 群，李国梁

(1.北京理工大学 光电学院机器人与系统教育部重点实验室, 北京 100081; 2.中国北方车辆研究所, 北京 100072)

在智能监控、安防、导航、侦察等领域中[1-4]，异构变分辨成像以其独特的优越性获得了越来越多的应用，典型的有复眼与人眼视网膜成像[5]。其中，人眼视网膜感光细胞因分布非均匀而具有中央凹的高分辨凝视观察优势[6]，即异构变分辨。同时，人眼视网膜从外界接受光强信息，并通过视觉传输神经传输到脑皮层的图像采集过程，类似于将图片从笛卡尔坐标映射到对数极坐标的过程[7-8]，使得人眼具有压缩冗余数据与抗旋转与尺度改变的特性。利用这种近似仿人眼分辨率通过对数极坐标进行变换后所得图像的旋转与尺度不变特性进行图像识别，减少了传统识别方法由于目标形变和尺度变化带来困扰[9]，从而达到更加快速、准确的目的[10]。

异构变分辨成像以对数极坐标作为基础，若想要利用对数极坐标下图像的旋转尺度不变性，需要精确的定位目标的位置，并调整成像系统视场将目标放置于视场中央[11-12]。一旦这种精确的定位产生偏差，图像的抗旋转尺度改变特性将会产生一定的误差，从而导致目标识别精度降低。

由于准确定位条件过于苛刻，在具体实践中往往难以完全满足。例如：在导弹瞄准过程中，若是可以精确的瞄准，目标相对于导弹旋转与缩放，通过对数极坐标进行了变化后的图像，具有良好的旋转尺度不变性。但由于飞行过程中因载荷本身振动或其他因素的影响[13]，目标和导引的视场中心之间会存在有一定的偏差，这种偏差使得获取的图像难以完全满足旋转与尺度不变条件，导致变换后的图像产生一定的误差。

目前，对异构变分辨成像中的视场偏心导致的旋转与尺度不变性性能下降尚未有相关研究报道。因此，从实际出发，通过对此类情况进行定量分析，研究目标在视场离心情况下的变化情况，从而为更好地应用异构变分辨成像提供技术支撑。

1 异构变分辨成像原理

1.1 变分辨采样与对数极坐标转换

人眼视网膜和视皮层之间存在类似于对数极坐标的非均匀映射关系。因此，构建类似对数极坐标的仿异构变分辨成像系统。在笛卡尔坐标平面中进行如图1(a)所示变分辨采样，再将其映射到对数极坐标平面中，即可得到相应的极坐标图像。笛卡尔坐标中像素位置用(x,y)表示，其对应的对数极坐标位置可以表示为：

(1)

其中，ξ和θ对数极坐标下的参数。

由图1可见在笛卡尔坐标中沿弧形排列的点在对数极坐标中沿着直线排列。在对数极坐标中等距离的纵向位移，会使笛卡尔坐标中采样点到原点之间的偏角相同，距离成倍增大，呈现出了中间高分辨率，外部低分辨率的异构变分辨成像。

1.2 旋转与尺度不变性

人眼视网膜与视皮层的对数极坐标映射具有旋转与尺度不变性的特性。

由式(1)可知，当位于笛卡尔坐标系中心的目标绕原点旋转α时，由于旋转后图像各点到原点的距离不变，即ξ=log(r)这一条件未发生变化，变化的仅仅是θ=arctan(y/x)条件，且变化后的θ′可表示为：

θ′=θ+α

(2)

可知笛卡尔坐标下的旋转变化转换到对数极坐标平面后，变成了θ的增减变化，即沿θ轴方向的平移。

图1 映射原理示意图

当目标以原点为基准变化成原来的q倍时，θ=arctan(y/x)条件不发生变化，可得

log(q)+log(r)=ξ+log(r)

(3)

从式(3)看出笛卡尔坐标下的尺度变化转换到对数极坐标下后，变成了ξ轴方向的平移。这种将旋转与尺度的变化转换为简单的一维平移变化的性质，即是旋转与尺度不变性。

1.3 视场偏差成像分析和归纳

在笛卡尔坐标下目标的旋转和尺度变化可以在极坐标中以平移的形式表现。但若目标在笛卡尔坐标平面发生的是位移变化，转换到对数极坐标平面下后，将会发生较为复杂的变化，如图2所示的五角星形视场偏差成像。

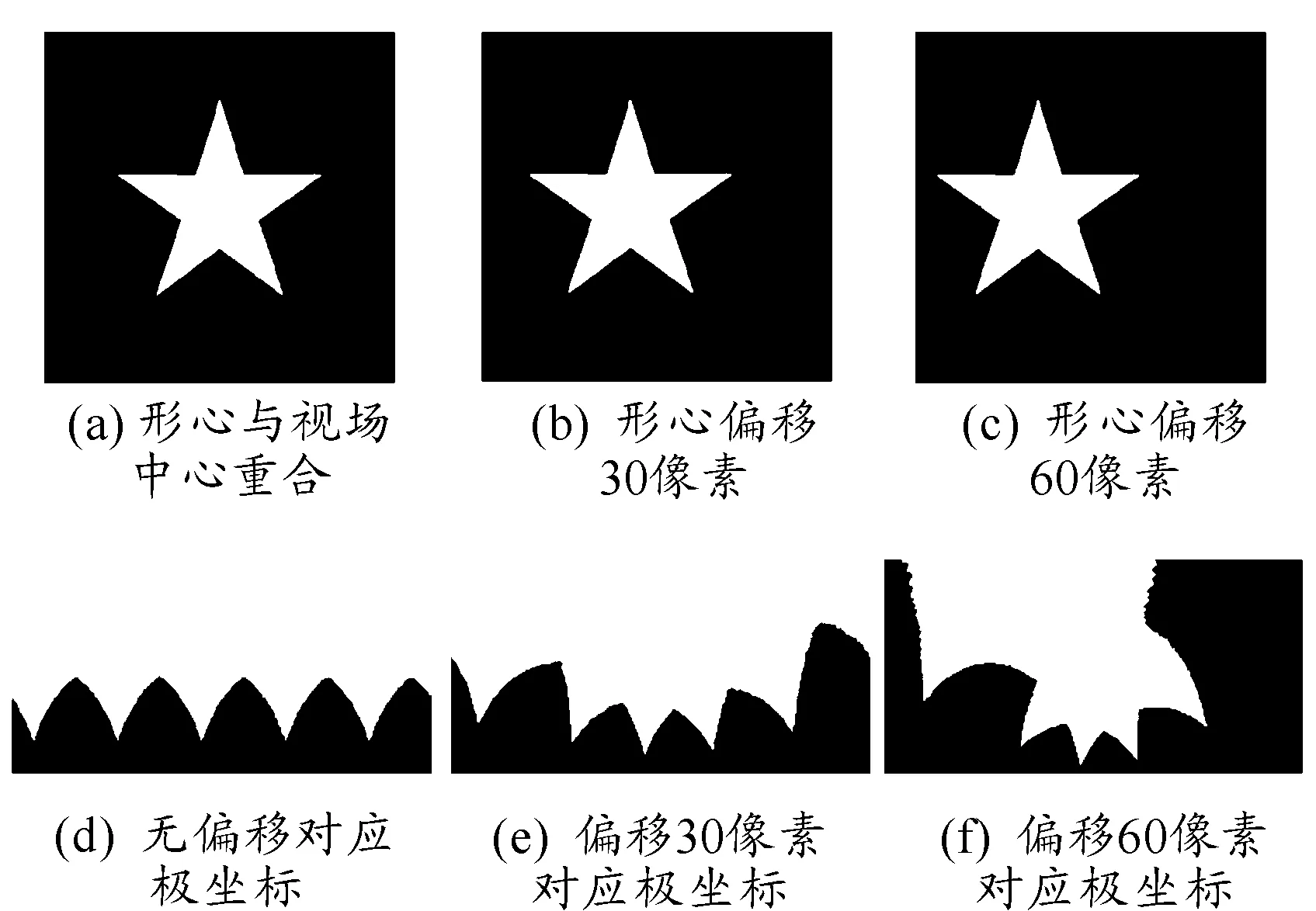
图2 五角星形视场偏差成像

由图2可知，随着目标偏离程度的增大，对应的极坐标图像呈现出一种向偏移方向收拢的趋势。这种在笛卡尔坐标系中简单的一维变换转换到对数极坐标系后，变成了复杂的二维变换，使得之后的工作复杂度急剧增大。

为进一步分析视场偏差成像模型，采用对数极坐标转换后成为直线的圆形目标，当其向x轴负方向偏移时，转换到对数极坐标下便成为了一种对称式的变化，较为直观，如图3所示。

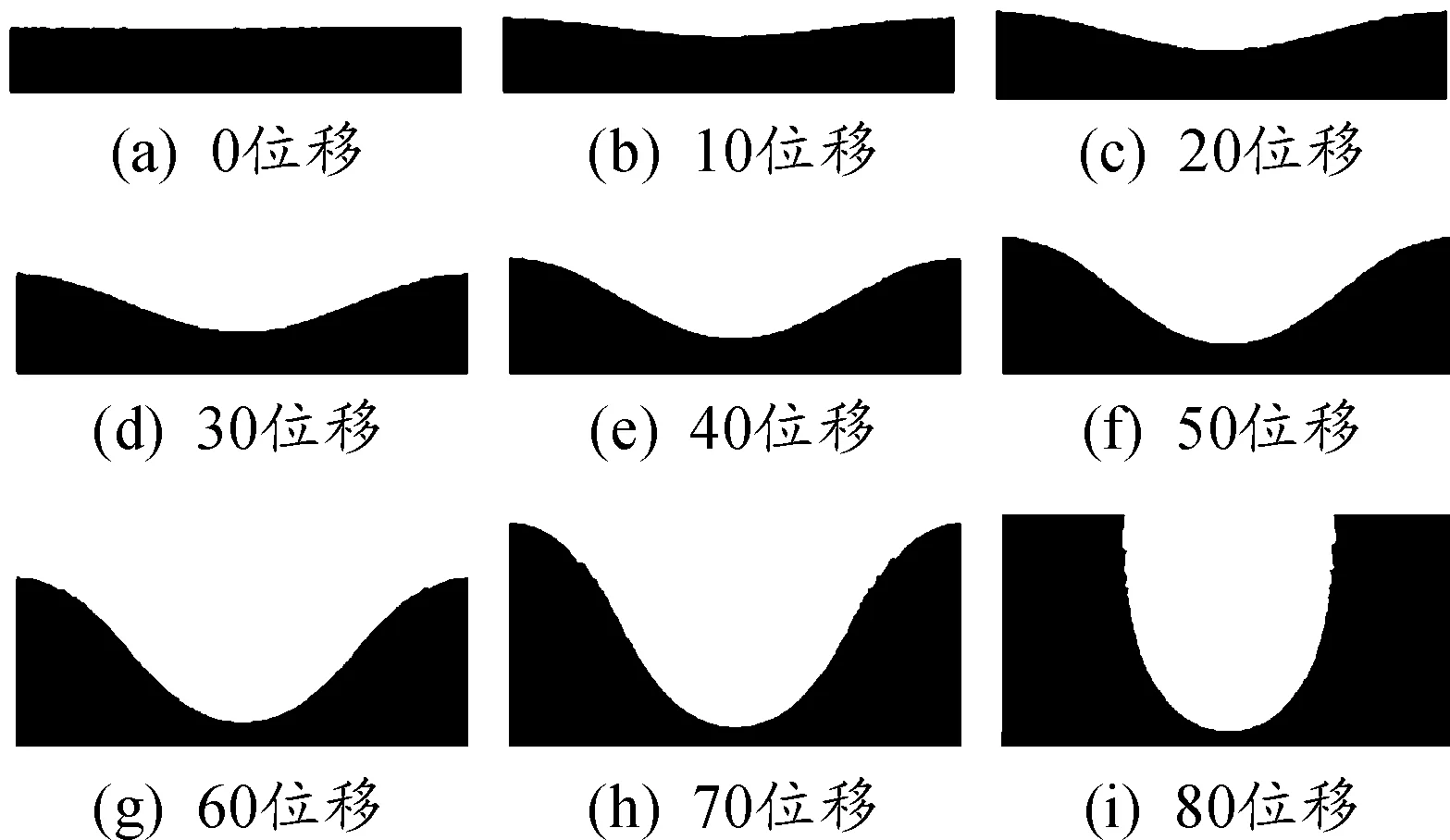
图3 圆形视场偏差放生成像

根据图3中0～80像素位移在对数极坐标平面下对应的图像，偏移使得原本的直线变成了一条中间凹陷、两边上扬的曲线，且曲线的曲率随着偏移量的增加而增加，说明对数极坐标对目标的平移变化不再有简化功能，对旋转与尺度不变性也可能存在一定的干扰。为此，后文将进行进一步的分析。

2 实验仿真与结果分析

2.1 仿真实验设计

对于从笛卡尔坐标变换到对数极坐标的图像，当目标位于视场中央时，具有良好的旋转与尺度不变性特性。但当目标形心与视场中心存在有偏差时，该特性的表现将会收到极大的影响，将偏移量与旋转角度作为自变量，研究其自小到大的变化对旋转与尺度不变性的影响。

为不失一般性，按照目标几何形状由简单到复杂，选择了如图4所示的3种目标：箭头形、五角星形以及无规律多边形。三次仿真具体参数如表1所示，对于旋转与尺度不变性存在误差的区域，采用了参数结构相似性(SSIM)进行客观评价，具体公式如式(4)。

(4)

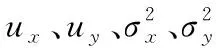
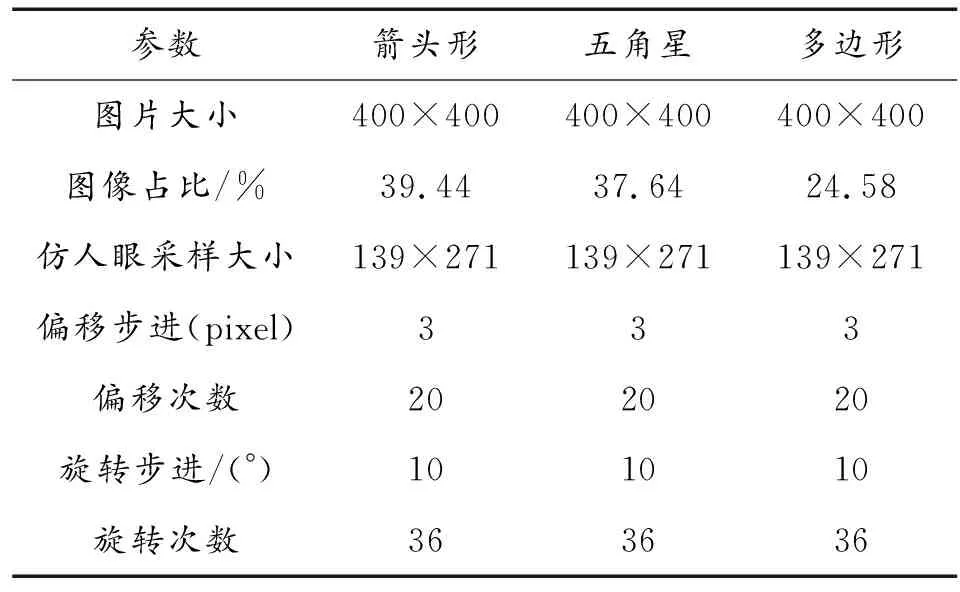
表1 三次仿真具体参数

2.2 仿真实验

2.2.1旋转变化

分析两种场景：目标位于视场中心的旋转以及偏心旋转，其中偏心旋转分为绕视场中心旋转和绕目标形心旋转两种方式。图5至图7为不同旋转情况下的成像结果。其中，图5至图7的(a)为形心与视场中心重合时的图像，其中：(b)为(a)逆时针旋转45°，(c)为目标向左偏移45像素图像，(d)为(c)中目标绕视场中心逆时针旋转45°，(e)为(c)中目标绕自身形心逆时针旋转45°图像。

将目标的不同形态(5种)按照对数极坐标变换得到第二排图像，观察其旋转不变性的效果，如图5～图7所示。

图5 箭头形旋转不变性验证

图6 五角星形旋转不变性验证

2.2.2尺度分析

对于在偏心后的尺度改变情况，进行上述类似的分析。考虑一般情况下，被测目标不会自发的进行膨胀或萎缩，故只考虑目标以视场中心为基准的缩放。图8～图10为不同缩放情况下的成像结果。其中图8～图10的(a)为形心与视场中心重合时的图像，其中：(b)为(a)放大1.5倍，(c)为目标向左偏移45像素图像，(d)为(c)以视场中心为基准放大1.5倍的图像。

将目标的不同形态(4种)按照对数极坐标变换得到第二排图像，观察其尺度不变性的效果。

图8 箭头形尺度不变性验证

图9 五角星形尺度不变性验证

图10 多边形尺度不变性验证

2.3 结果分析

通过上述仿真，可以看到：

1) 当目标形心与视场的中心重合时，如图4(a)和图4(b)所示，视场的旋转和目标的旋转是等价的，符合旋转不变性的特点，其对数极坐标下的图像仅仅发生了横向的移动。

2) 当目标形心和视场中心之间存在偏移时，围绕目标形心的旋转不会影响目标在视场中的相对位置，仅仅是自身的形态发生了变化，如图5(c)和图5(e)所示；但若围绕着视场的中心进行旋转，则在目标形态发生变化的同时，其相对位置也发生了相应的偏移，如图5(c)和图5(d)所示。将三幅图片转到对数极坐标平面下，围绕视场中心旋转的两幅图片图5(h)、图5(i)仅仅发生了横向的偏移，符合旋转不变性的特点；但围绕目标形心旋转的两幅图片图5(h)和图5(j)之间的变化不再局限于一维的变化，在沿着横坐标偏移的同时，有着向某一点收拢的趋势。

3) 无论目标形心与视场的中心是否重合，如图8(a)和图8(c)所示，在缩放基准为视场中心时，均符合尺度不变性特性，其对数极坐标下的图像发生纵向的移动。

综上，对于目标旋转的情况：理想状况下的旋转不变性不再局限于目标形心与视场中心重合的情况，只需保证目标的旋转中心是视场中心，旋转不变性特性依旧存在。对于目标尺度改变的情况：以视场中心为基准进行缩放同样符合尺度不变性特性。但对于旋转中心不再是视场中心的情况，旋转不变性将会受到一定的影响，因此需要进一步分析可行区间。

2.4 可行区间的分析

由2.3节获得的结果，旋转不变性的适用范围仍局限在仅在很小的范围内，且对于目标形态的改变方式也有着十分严格的限制，旋转不变性的应用范围仍十分苛刻。为进一步提高旋转不变性的适用范围，容忍一定的旋转不变性误差。利用结构相似度对绕视场中心旋转和绕目标形心旋转后，对对数极坐标平面所得到的图像进行评价，若绕视场中心旋转的对数极坐标图像和绕目标形心旋转的对数极坐标图像结构十分相似(结构相似度在0.9以上)，则近似的认为绕目标形心旋转的图像仅仅是像绕视场中心旋转的一个位移变化，近似的符合旋转不变性。

按照表1中确定的仿真实验的具体参数，以偏移量和旋转角度为x、y轴，结构相似度为z轴，画出结构相似度随着参数变化的趋势图，如图11(a)、图11(b)、图11(c)所示。可知，当旋转角度为0°和360°时，即目标未发生旋转，其结构相似度为1，对数极坐标中的图像完全相同；当位移为0时，即目标形心与视场中心重合，其结构相似度也为1，对数极坐标中的图像完全相同。

图11 不同图形位移旋转SSIM值计算

当旋转角与偏移同时存在时，绕视场中心旋转和绕目标形心旋转后，转换为对数极坐标平面所得到的图像将会存在一定的差异，其结构相似度开始降低。在旋转角度与偏移量构成的坐标系中，画出结构相似度为0.9的曲线，如图11(d)、图11(e)、图11(f)所示。可见对于不同的位移，在可以容忍的误差程度内，其旋转角度是不同的。位移越小，可旋转的角度越多。在位移不大于3像素的情况下，目标可以在360°的范围内旋转；位移大于3像素时，可以容忍的旋转角度急剧减少，最终接近于0。

将保持旋转不变性条件下的旋转角度累加到偏移量坐标中，同时统计向多个方向的结果，以亮度作为可旋转角度参考量，画在视场平面中，获得在容忍范围内的旋转角度与各个方向偏移量之间的关系，如图12所示。

图12 可行区域仿真

图12中分别为3种目标在笛卡尔坐标下的仿真。可见对于同一目标，在各个偏差方向上，其可容忍的旋转角度随位移偏差的变化情况相似，在坐标系中呈现出一个个不同亮度环状的区域，其中亮度越亮得地方代表着可容许的旋转角度越大。

目标的偏移可行区域是允许目标以自身形心旋转，而其转化为对数极坐标后的图形与理论中符合旋转不变性所得的图像十分相似的区域。即两种旋转后所得图片可以在之后的处理中近似认为成同一目标。这种容忍性需要包含旋转的各个角度，所以其容忍的旋转角应为360°，即为图中最亮的区域。可见，3种典型目标的旋转可行均为中心直径为6像素的圆形区域。

3 结论

在图像匹配、目标识别的过程中，利用异构变分辨成像的抗旋转与尺度改变特性可以很好的解决目标变化带来的识别误差。对于这种使用方便但适用条件严苛的特性，利用结构相似度对其适用范围进行扩展。本文深入讨论了离心情况下满足此特性的区域，并以典型几何形状目标作为分析对象，通过对目标进行多角度旋转情况分析，找到了目标在不同偏心大小和旋转角度的情况下，异构变分辨成像的抗旋转与尺度的可行情况，并进一步确定了中央区域直径为6像素的圆形区域作为可行区域，使得在目标对准的过程中可以容忍约3%的误差存在，为异构变分辨成像的实际应用提供理论支撑。