基于BP神经网络的某反装甲武器系统打击效果预测
迟明祎,侯兴明,陈小卫,周 瑜
(1.航天工程大学 航天保障系, 北京 102200; 2.中国解放军63850部队, 吉林 白城 137001;3.中国解放军32183部队, 辽宁 锦州 121000)
在作战模拟和计划制定、作战试验方案设计的过程中,火力打击效果的预估是预测体系作战效能的关键,是合理配置作战资源、正确组织火力毁伤行动的依据[1],也是作战试验方案评估的重要方法。
现代陆地战争不断发展变化,便携式反装甲武器经过了半个多世纪“四代”的发展,战术技术性能明显提升,已经成为战场上抵挡装甲机械化步兵团突击的尖端利器[2]。反装甲武器诞生时间长,作战和演训中的应用场景较多,随着便携式反装甲武器系统的智能化程度的提升,弹丸的造价也越来越高,考虑到试验成本和周期问题,在试验阶段不可能将所有的影响因子任意组合设计试验科目以得到所有因子组合场景下的试验结果。立足靶场已经积累的试验数据,设计一种火力打击效果预测模型,预测各个影响因子在不同组合情况下反装甲武器的打击效果,从而辅助指挥员决策,为作战筹划服务很有必要。
当前关于对武器系统打击效果的预测方法,主要有专家评议法、统计分析法、数学解析法等[3-4]。然而,专家评议法过多依赖专家的经验素质和推理能力,主观因素较多;统计分析法需要分析大量的数据进行归纳总结,当影响因子较多且之间关系极为复杂时,统计分析方法很难实施;数学解析法不能避开打击效果与影响因子之间复杂的机理关系的分析[1,3,5-8]。上述方法在处理反装甲武器系统打击效果预测问题上均存在缺陷。
近年来,随着神经网络、机器学习和人工智能的迅猛发展,神经网络方法已经开始逐渐运用于军事领域问题的分析,作为一种“黑箱”模型算法,神经网络具有很强的容错和自学习能力[6]。而基于梯度下降法的3层BP神经网络在解决复杂非线性问题方面非常有优势[3]。来自印度共生国际大学的学者L.V.Kamble[9]在文章中运用了梯度法向传播的神经网络模型用于模拟水平管在大颗粒气固流化床中的传热预测,预测结果与实验值非常吻合。来自Mahakal理工学院机械工程系的学者Shrikant Pandey[10]借助人工神经网络(ANN)预测室内温度,使用实验数据作为训练样本,运用traingdm,traingdx,trainrp等多种训练算法训练模型,经比对发现traingdx梯度下降法这种方法具有计算速度快,通过自适应学习逐步提高性能,自组织和实时的优点。刘芳等[4]指出,部分学者将一般神经网络和支持向量机运用于预测分析中,但是会出现训练神经网络训练速度慢,易陷入局部最小解的问题以及支持向量机对缺失数据的极度敏感问题。谭丽萍等[6]借助基于traingdx函数梯度下降法的三层BP神经网络解决GNSS高斯拟合问题,得出选用 traingdx 梯度下降训练法作为训练函数,效果最佳,拟合精度好于其他训练函数的结论。
根据上述观点,本文根据反装甲武器打击效果与因素间的复杂关系特性,神经网络的功能特性,采用基于改进的融合小波函数梯度下降法BP神经网络构建预测模型,避开对系统内部复杂的机理和关系的分析[1],直接借助以往作战试验产生的数据样本对模型进行训练,通过反复修正,确定网络结构和参数,实现对某型反装甲武器系统的打击效果的预测,从而为指挥员的决策部署、作战筹划和试验方案设计的评估提供依据。
1 反装甲武器系统打击效果影响因子分析
以射程对打击效果的影响为例,选取两种情况下射击科目的试验数据生成打击效果随射程变化的曲线,确保在每组数据中射程为唯一变量。
从图1可以看出:在不同条件下,打击效果的量值有差异,且曲线的变化趋势也不相同;即使在同等条件下,打击效果随射程增加呈非呈线性变化。通过分析将可能的原因归结如下:
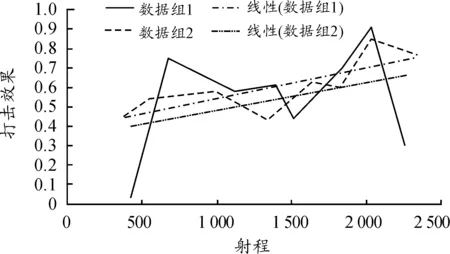
图1 打击效果随射程变化曲线
1) 在一定范围内射程增加会增加弹丸的动量,对打击效果呈正向作用;
2) 在一定的范围内射程的变化会导致弹道末段弹丸速度变化,从而导致炸点与靶面的距离的变化,导致打击效果变化;
3) 在一定范围内射程的变化,弹丸飞行期间靶车会产生位移,导致弹丸中靶或空爆时的入射姿态发生变化,从而导致打击效果发生变化;
4) 射程的变化还会对其他的影响因子如超压峰值、正压作用时间产生影响,共同作用于打击效果。
通过对历史数据的分析可知,装甲目标的打击效果与其影响因素之间呈十分复杂的非线性关系,各因素对目标的打击效果的影响大小和方向各不相同。为了解决反装甲武器系统打击效果的预测问题,首先要确定反装甲武器系统打击效果的影响因子有哪些。
在近几年的高机动步兵营反装甲火力运用能力试验中,数据采集技术人员伴随采集有关参数达三十多种,其中只有部分因素对反装甲武器打击效果产生影响,且其影响大小和方向也各不相同。构建模型时影响因子过多会使模型结构复杂化,增加模型实现的难度,因子有遗漏会导致模型预测不准。结合Delphi专家评议法、部队调研、试验部队操作经验、试验保障人员的经验判断以及绘制分析单个因子对打击效果的影响曲线等方法,经过反复的分析和实验(当影响因子选取有遗漏时,可能造成神经网络不收敛),得出反装甲武器系统的十一个影响因子如下:中靶时刻弹丸瞬时速度(m),炸点与靶面轴线距离(m),中靶时刻目标运动速度(m/s),掩体高度(m),射程(m),冲击波强度(kPa),正压作用时间(s),射手熟练程度(按九等级划分法分为极差、差、较差、不合格、合格、较好、良、优良、优并分配量值区间)。自然环境条件3个:天时(按昼夜赋值量化),天候(按光照强度分级量化),风速(m/s)。
首先进行部分数据的量化和归一化的预处理。对于定性指标的量化,如射手熟练程度指标,按照经典的标度对照法,划分极差、差、较差、不合格、合格、较好、良、优良、优,对应0.1、0.2、…、0.8、0.9[12]。定量指标的常用的规范化方法有标准化法,比重法与阈值法[13]。比重法的优势在于经变换之后较客观反映原始指标间的关系,考虑了指标值间的差异性,前提是所有量化指标都满足xi≥0[14]。本文采用比重法进行规范化处理的方法如下[14]:
(1)
其中:xi为第i个样本数据;yi为规范化后的值。
2 模型构建
一般认为,神经网络结构越复杂,层数越多,节点数越多,模型往往具有更好网络性能和泛化能力,但是缺点是相应会增加运算量,增加实现的难度,所以选择适合于反装甲武器系统的打击效果预测的神经网络模型是关键。一般首选3层网络,即只含有一个隐层的神经网络,可适当调整隐含层的神经节点数,增加隐层节点数要比增加隐层数更容易实现[1,11,13]。在理论上已经证明,一个包含一个隐含层的3层神经网络可以以任意的精度逼近任意一个非线性函数,前提是隐含层的神经元数可以任意调整[1,15]。
2.1 基于BP神经网络的反装甲武器打击效果预测模型算法流程
BP神经网络(Back-ProPagation Network)是一种信号沿正方向单向传播而误差经过反馈沿反向传播的神经网络,拥有输入层、至少一个隐含层和输出层的多层网络[6]。BP学习算法是多级非循环的训练算法,其基本思想是利用最小二乘法和梯度搜索技术,以期使网络的实际输出与期望输出之间的误差均方差为最小,网络学习过程是一个误差边传播边修正网络参数的过程。根据BP神经网络的理论原理和问题特性,基于BP神经网络的反装甲武器打击效果预测模型的算法流程如图2所示。
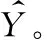
步骤2:设置神经元间连接权系数和神经元阈值初始值。对神经元间连接权系数和神经元阈值进行初始化,随机取[-1,1]之间的值(其中权重极值1表示正相关,-1表示负相关),所有节点参数的变化量和学习率变化量初始化为0,设置初始学习率初始值和误差容许值Rallow。
步骤3:计算第t次迭代隐含层和输出层的输出值。信息沿着神经网络节点间的通路由输入层向输出层逐层正向传输,计算各层的输出值Oj,j表示第j个节点:
(2)
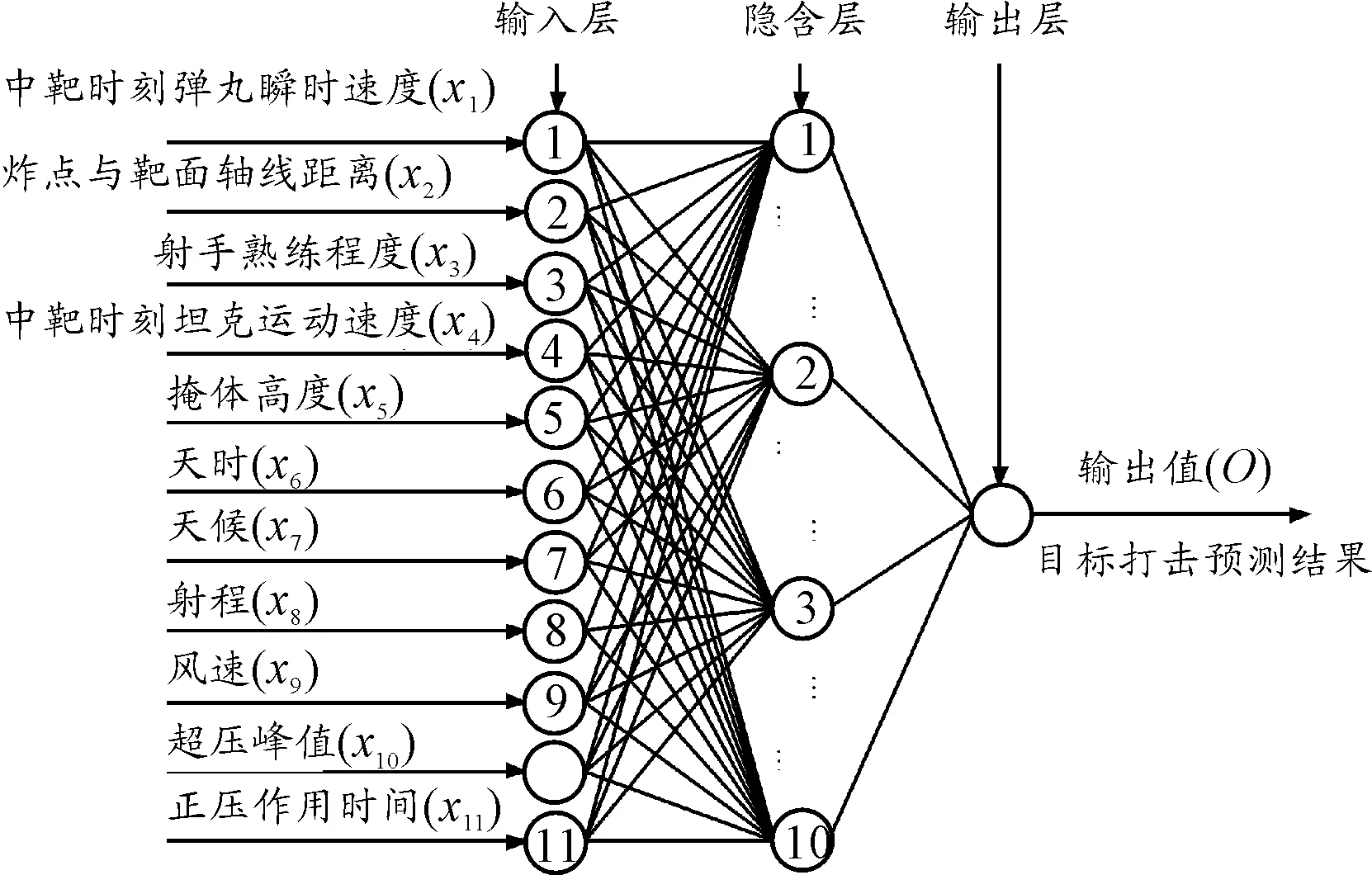
假设相邻两层节点之间一一连接,同层节点之间无连接。其中,n表示节点j的输入节点数,xi是第i个输入节点的输出值,神经网络中输入层的输入到输出一般不做运算所以xi等于Xi,wji是输入层第i个节点到下一层第j个节点的连接权系数值,θj表示阈值。神经元节点连接关系如图3所示。
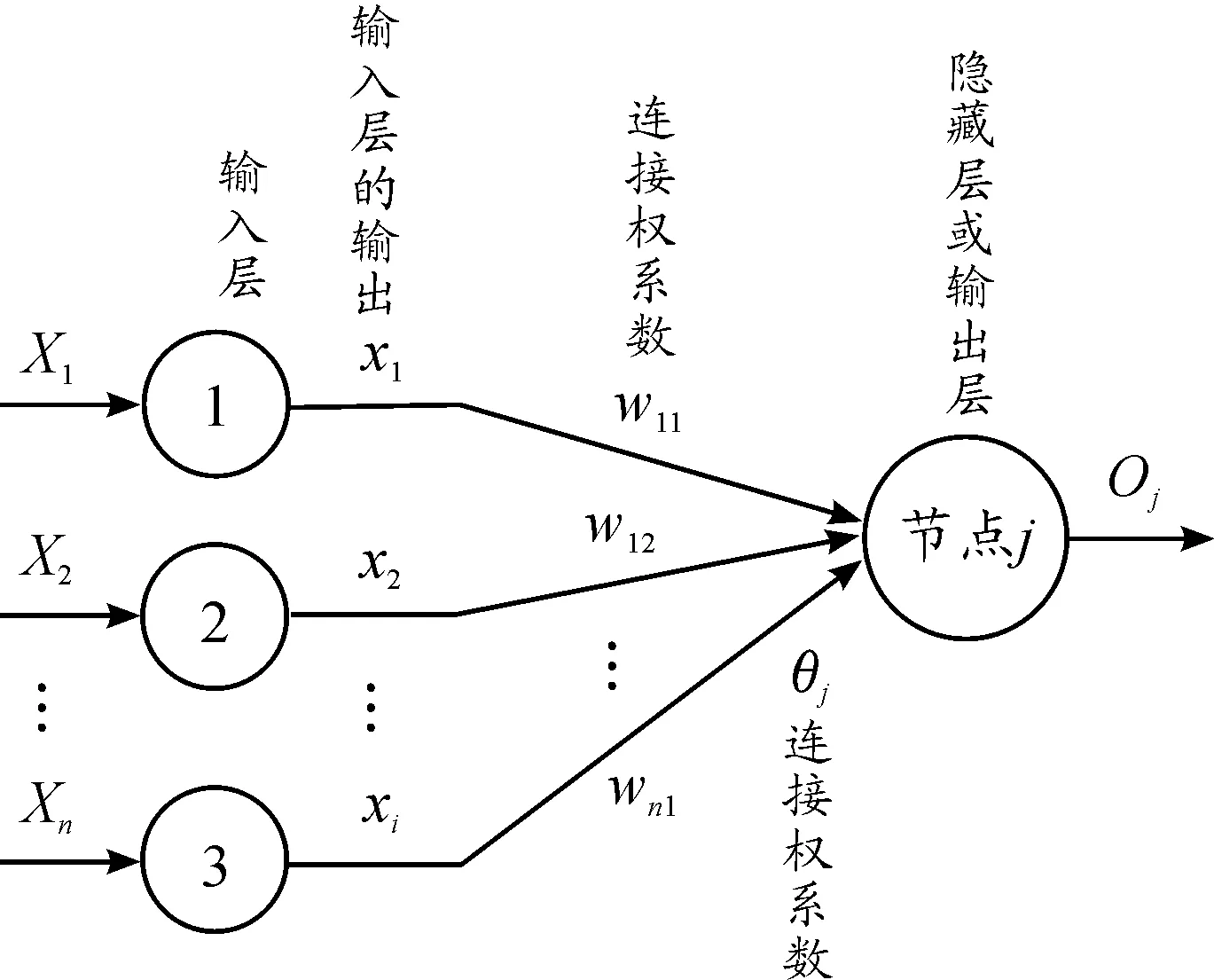
图3 神经元节点连接关系示意图
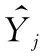
(3)
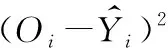
wji(t+1)=wji(t)+ηδjoj+a[wji(t)-wji(t-1)]
(4)
θj(t+1)=θj(t)+aδj
(5)
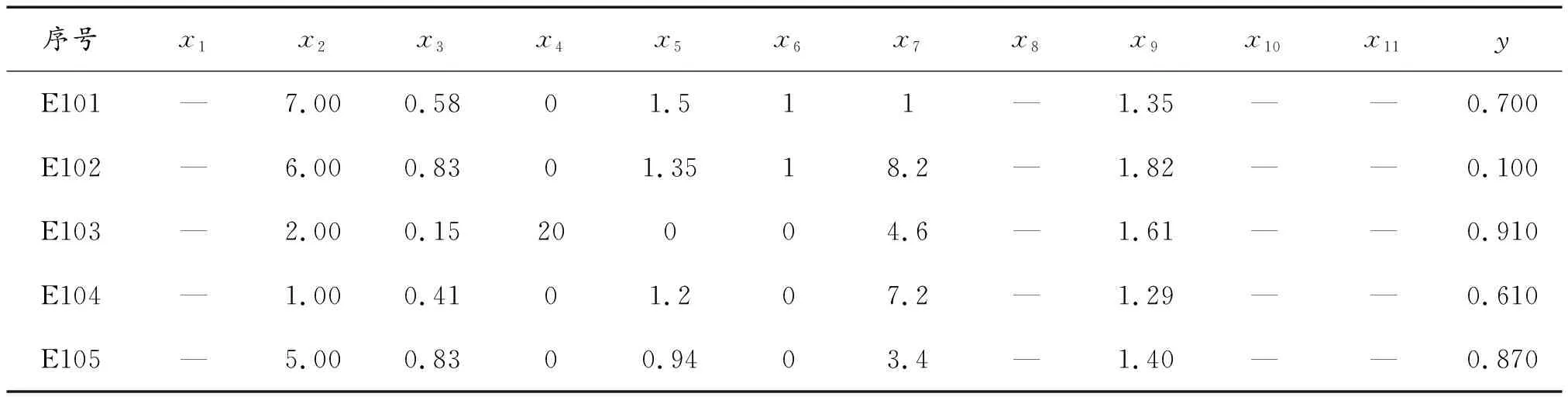
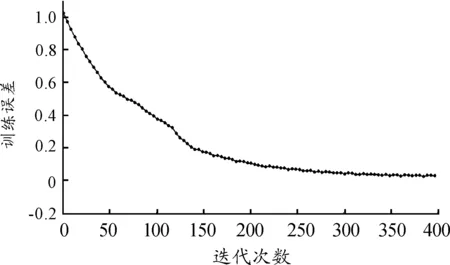
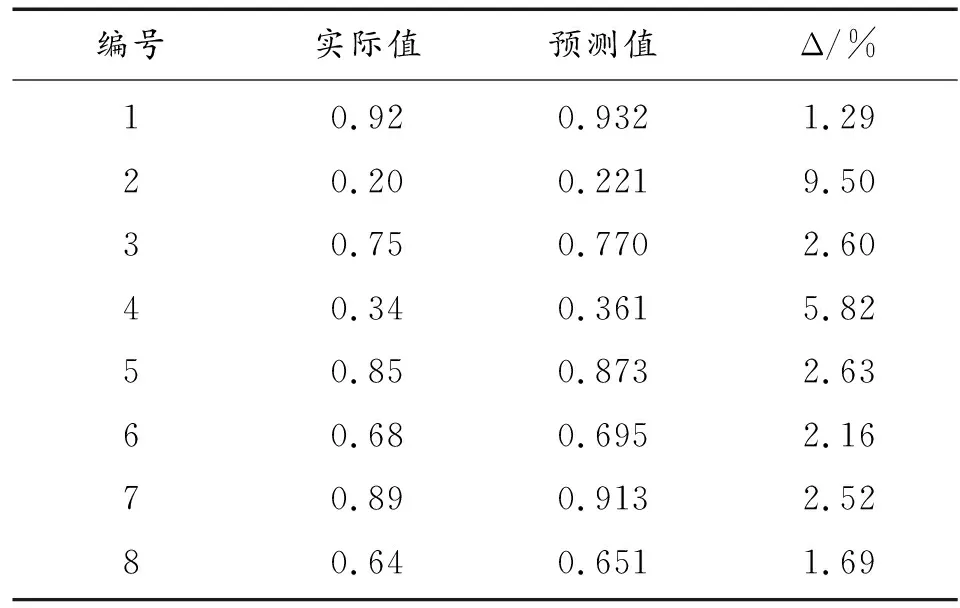
其中:t、t+1,t-1表示该迭代次序;η是学习系数(也称为学习步长,0<η<1);a是冲量系数(0 1) 如果节点j在输出层,遵循: (6) 2) 如果节点j不在输出层,在其他各隐含层,因没有期望输出值,无法进行输出值比较,则遵循: (7) 式(7)中,假设j层的输出节点总数为k。 转到步骤3进行第t+1次循环计算。 步骤5:训练结束,用某次试验数据检验神经网络的训练效果,对火力打击效果的量值进行预测。 上述预测算法流程是一个迭代过程。每一轮执行中将连接各权系数值和阈值调整一次,进入下一次计算,迭代循环进行下去,直到期望输出与计算输出的均方差小于预设的容许值,学习训练阶段结束,模型形成较好的包络,预测模型建立。 本例中,输入层神经元个数为11,输出层节点数为1,则根据BP神经网络隐含层设计经验公式[17]: (8) 式(8)中:mhidden表示隐含层节点数;nin表示输入层节点数;lout表示输出层节点数;h为1~10之间的整数。 考虑本文所研究的问题的实际情况,经过反复尝试验证,最终确定隐含层神经节点个数为10,即形成了具有11-10-1网络结构的某型反装甲武器系统目标打击效果BP神经网络预测模型,如图4所示。 BP神经网络预测结果的准确性主要受网络结构、样本的代表性与训练函数选取三方面的影响[18]。选取不同的训练函数,训练的速度和样本拟合的精度不同。为了减小局部最小解出现的可能,在各种训练函数中,Matlab软件中的traingdx函数的精度效果比较好,故选取traingdx作为神经网络隐含层训练函数。traingdx函数是一种带冲量(momentum)的并且具有自适应学习速率(lr,learning rate)的梯度下降算法函数[4],通常用来解决在隐含层神经节点数较少的情况下的拟合问题。 图4 11-10-1结构的BP神经网络预测模型示意图 采用小波函数作为隐含层神经元的激励函数,可增加神经网络结构的学习功能[19],提高模型的训练效率,同时可降低局部最小解出现的情况。输出节点的激励函数通常是非线性可微的,常采用Sigmoid函数作为输出层神经元激励函数。Sigmoid函数的表达式如下[20]: Sigmoid函数: (9) 神经网络的输出输入关系表达式如下: (10) (11) 至此,火力打击效果预测神经网络模型的迭代在于求解模型参数,即包括尺度变量aj、平移变量bj、输入层到隐含层的连接权系数、阈值、隐含层到输出层的连接权系数v1j、 阈值λij。基本数学方程如下: (12) BP神经网络预测结果的准确性主要受网络结构、样本的代表性与训练函数选取三方面的影响[18]。在近几年开展的历次作战试验产生的大量的历史数据样本中,选取底层参量和输出量值均匀分布的并且具有代表性的105组数据作为本模型的训练样本,在算法中首先进行了数据的量化和归一化的预处理。其中,部分训练样本中原始数据如表1所示。 表1 打击效果预测模型训练样本原始数据 将第1~105组数据作为训练样本输入模型,设置训练允许误差Rallow为0.01,最大迭代次数为1 000。用Matlab软件进行训练,输出误差随迭代次数的变化曲线如图5所示。 图5 基于Matlab软件的训练误差随迭代次数变化曲线 由图5可以看出:当大约进行300次训练时,输出误差达到最小。将反装甲火力运用能力试验实测的历史数据挑选第106~113共8组数据作为检验样本,输入预测模型,将打击效果的预测值和真实值作比对,对比结果如表2所示。 借助平均绝对百分比误差(MAPE)对预测效果进行评价,其计算公式如下[21]: (13) 表2 神经网络模型预测结果 通过对某型反装甲武器系统打击效果影响因子分析基础上,运用融合小波函数的改进的梯度下降法BP神经网络仿真建模技术,构建影响因素和打击效果量值之间的关系模型,借助历史试验数据样本对模型进行训练。借助新的历史试验数据对模型的预测效果进行检验,通过数据对比结果可以看出,该预测模型预测性较好。通过建立基于改进的梯度下降法BP神经网络的预测模型,可实现对该武器系统打击效果有效预测,可为火力打击方案拟制、试验方案评估和武器装备性能改进提供科学依据,也为海量作战试验数据的分析、挖掘和再利用提供了思路。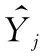
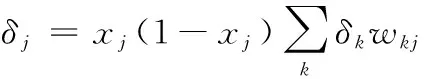
2.2 BP神经网络预测模型结构设计
2.3 BP神经网络预测模型训练函数选取
2.4 BP神经网络预测模型激励函数的改进
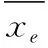
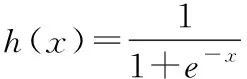
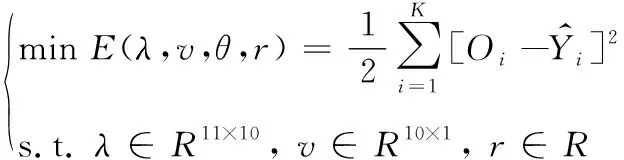
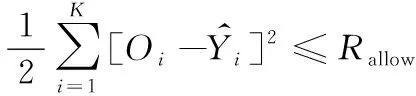
3 算例分析
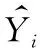
4 结论

