优化运算策略 落实运算素养——以“圆锥曲线中运算优化策略的研究”教学公开课为例

李 刚

(江苏省木渎高级中学，215100)

《普通高中数学课程标准(2017年版)》指出:数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果等[1].由此可见,数学运算是学生数学学习中的一种必备能力,是逻辑推理的具体表现.不同层次的运算素养水平彰显了学生不同层次的数学思维品质[2].随着新一轮课改的逐步推进,如何在教学中提高学生的数学运算素养水平,发展学生的数学思维能力,是我们每一位数学教师应该思考的问题.

本文结合教学中的例题以及学生的解题方法谈谈对学生数学运算素养的培养.

一、案例剖析

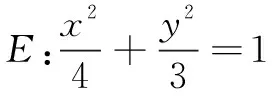
第一层次:直接翻译,正确运算

初看此题,思路比较清楚,既然要求点P的坐标,不妨直接设点P的坐标,通过条件得到点Q的坐标(用点P的坐标表示),代入椭圆方程,进而可以建立关于点P的坐标的两个方程,联立解得点P的坐标即可.在课堂上,大部分同学选择了此种方法.

课程标准对数学运算素养水平中有关水平一的部分描述为:能够在熟悉数学情境中了解运算对象,提出运算问题;能够在熟悉的数学情境中,根据问题的特征形成合适的运算思路,解决问题[1].解析几何方法就是把几何问题转化为代数问题,在用代数方法解决几何问题的过程中往往会涉及到比较多的复杂的运算.

第二层次:挖掘内涵,合理运算

在数学运算素养水平中有关水平二的部分描述为:能够在关联的情境问题中确定运算对象,提出运算问题;能够针对运算问题,合理选择运算方法、设计运算程序,解决问题[1].

我们知道,向量是一种运算对象,向量方法也可以将几何问题转化为代数问题.对于两个垂直关系,我们也可以从向量的数量积为0的角度思考.于是,设计问题1.

问题1除了用斜率之积为-1来处理条件中的两个垂直关系之外,我们还可选择哪些运算对象来刻画垂直关系?

设计问题1的主要目的就是引入向量这样一种运算对象.

解法1设P(x0,y0) (x0>0,y0>0),Q(x1,y1),

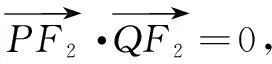
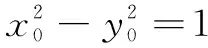
解法1虽然引入了点Q的坐标,感觉上引入的参数较多,但两个数量积为0所得的代数式可以通过整体思想进行化简,找到坐标之间的等量关系,进一步探求解题思路.对于本题,有着比较丰富的几何背景,笔者在教学中设计了如下两个问题和学生一起探讨.

问题2如图2,观察图中的∆PF1F2和∆QF1F2,这是两个焦点三角形,在处理焦点三角形问题的时候,我们有哪些思考的角度呢?

通过问题2,主要是让学生联想到焦半径,进而回想椭圆的第一定义和第二定义,从这两个方向进行思考.

问题3如图2,由条件PF1⊥QF1,PF2⊥QF2,你能从几何角度建立这两组焦半径之间的关系吗?

问题3是让学生通过问题2联想到了焦半径后,根据条件中的两个垂直关系,通过构造直角三角形建立两组焦半径之间的关系,进而求得所求量.

通过上述两个问题的创设,学生得到了以下两个处理的角度.

解法2角度1(利用椭圆第一定义)

如图2,连结PQ.设PF1=m,QF1=n.

由PF1+PF2=4及QF1+QF2=4得PF2=4-m,QF2=4-n.

当PF2⊥x轴时,l1与l2相交于F1,不符合题意;

当PF2不垂直于x轴时,因为PF1⊥QF1,PF2⊥QF2,

m2+n2=(4-m)2+(4-n)2,整理得m+n=4,即PF1+QF1=4.

又PF1+PF2=4,所以QF1=PF2.根据椭圆的对称性得到xP=-xQ.以下过程略.

角度2(利用椭圆第二定义)

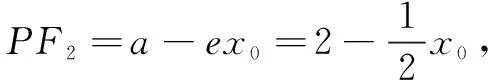
当PF2⊥x轴时,l1与l2相交于F1,不符合题意;

解得x1=-x0.过程略.

第三层次:优化路径,以思助算[2]

问题4在解法2中我们通过连结PQ，得到两个有公共斜边的Rt∆PF1F2和Rt∆QF1F2(如图3),从几何角度观察,点P,Q,F1,F2有关联吗?

问题4主要是充分挖掘图形的几何特征,利用两个直角三角形有公共直角边这一特征,得到P,Q,F1,F2四点共圆,并且此圆以PQ为直径.根据椭圆的对称性,所以有圆心在线段F1F2的中垂线上，或者正好是原点.

解法3因为PF1⊥QF1且PF2⊥QF2,所以焦点F1,F2在以PQ为直径的圆上.

因为P,Q均在椭圆上,所以圆心在线段F1F2的中垂线上(如图3)或圆心为原点(如图4).

设P(x0,y0) (x0>0,y0>0).

① 若圆心在线段F1F2的中垂线上(如图3),则以PQ为直径的圆的方程为

二、几点思考

1.明确运算对象,把握运算目标

2. 合理选择对象,设计运算思路

数学运算能力不仅是学生的数学操作能力,更是学生的数学思维能力.在同一数学情境中,不同的运算思路、运算程序的设定,体现了一定的规划设计能力[2].在实施运算分析和解决问题的过程中,要力求做到善于分析运算条件,探求运算方向,选择运算方法,设计运算程序,使运算符合算理,合理简洁[3].

在上面例题解法中,解法1是学生都能想到的方法,从运算对象角度分析,通过设点P的坐标,后面就是数与代数式的运算.如果能够进一步思考,从垂直这一关系深入挖掘,通过引入向量这一运算对象,可以得到解法2,关注焦点三角形这一运算对象,可以得到解法3.对运算对象的不同理解,可以得到不同的运算思路.

3. 挖掘运算内涵,发展数学思维

提升学生的数学运算素养,不仅仅是提高学生的运算速度和解题技能,在教学中,要培养学生对运算对象的含义、作用的理解.高中阶段,除了掌握数、字母的运算对象,还需要进一步掌握向量等运算对象,深刻体会其内涵.比如上面例题中的解法2,较好地运用了向量的性质解题,比解法1简单多了,所以应该善于观察,充分利用运算对象(向量)来简化运算.

4. 亲身体验过程,优化数学品质

有些学生在数学学习中,特别是在解析几何的学习中,产生想法后就忽视了运算;同样也存在部分教师在处理解析几何这部分内容时,只讲思路而忽视运算.这些现象导致了部分学生害怕运算,甚至是不会运算.其实通过上面几点的分析,忽视学生的亲身体验,更多的是带给学生种种数学素养能力的缺失.因此,只有让学生亲身经历完整的运算过程,把分析运算条件、探求运算思路、设计运算程序、解释运算结果这些过程还给学生,才能充分培养他们的运算素养,优化他们的数学品质.