在探究中培养学生的数学思维能力

北京市顺义牛栏山第一中学 胡亚萍 张传海

在教学素材的选择过程中,善于挖掘发现题海中那些绚丽的珠贝,那些对学生的学习过程、学习体验有深远影响的问题,运用到教学过程中,能够很好地优(效率高)化、雅(不落俗套)化、趣味化教学的过程,从而更好地培养学生的思维能力.

甄选好的素材,进行一题多解的课堂教学就是其中一种方式.但是,这些方法是怎样产生的?他们之间的逻辑关系又是怎样,思考解决方法时学生的思维活动是怎么展开的,有什么规律?通过这个过程学会什么?这是学生要逐步学会的,学会学习,学会思维.

下面就是一个很好的问题.

如图,在三角形ABC中,D为BC的中点,F为AB边所在的直线上一点,连接CF交直线AD于点E,若,求的值.

分析:本题中的条件是两个比例关系,D为BC的中点,所求也是一个比例关系,求的值.站在知识系统的角度来考虑,与之相关的是平行线分线段成比例定理以及三角形相似的知识.但是问题中并没有平行线,因此,问题解决的核心工作就是——大胆尝试着作出平行线、得到相似形,得到比例关系,建立已知和求解的联系.

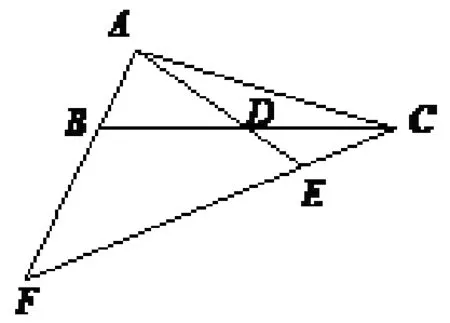
例题图

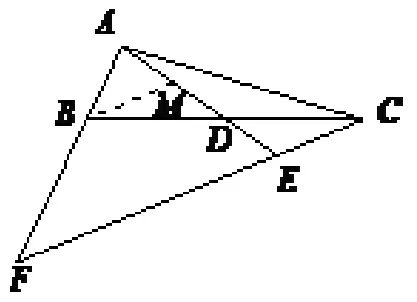
图1

探索一:从点B作平行线

解法一:(如图1) 过点B作CF的平行线交AE于点M,因为BD=DC,∠BDM=∠CDE,∠DBM=∠DCE,所以∆BDM∆CDE,所以BM=CE,又因为所以所以所以求得.

解法二:(如图2) 过点B作AE的平行线交FC于点M,因为BD=DC,所以ME=CE,又因为所以所以.

图2

图3

探索二:从点D作平行线

解法三:(如图3) 过点D作AF的平行线交CF于点M,所以∆EDM∆EAF,∆CDM∆CBF.因为BD=DC,所以BF=2DM,同时有FM=MC,又因为所以所以所以AF=3DM,故有AB=AF−BF=DM,所以.

解法四:(如图4) 过点D作CF的平行线交AF于点M,所以∆BDM∆BCF,∆ADM∆AEF.因为BD=DC,所以BM=MF且有又因为所以故有所以AB=BM,求得.

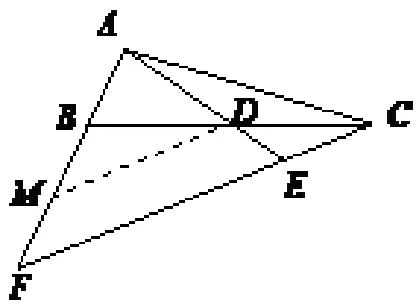
图4

图5

探索三:从点E作平行线

解法五:(如图5) 过点E作AF的平行线交CB于点M,所以∆CME∆CBF,∆EDM∆ADB.因为所以因为BD=DC,所以所以故BF=2AB,求得

解法六:(如图6)过点E作BC的平行线交AF于点M,所以∆ABD∆AME,∆FME∆FBC.因为CE=则因为BD=DC,故有即所以由得FM=3BM,由AB=所以.

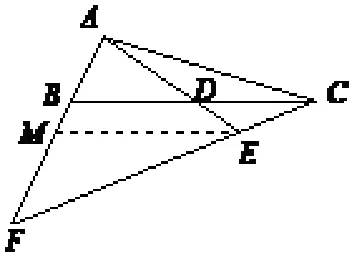
图6

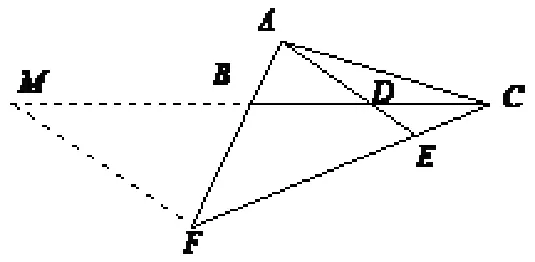
图7

探索四:从点F作平行线

解法七:(如图7) 过点F作AE的平行线交CB延长线于点M,所以∆CDE∆CMF,∆ABD∆FBM.因为所以因为BD=DC,所以求得.

解法八:(如图8) 过点F作BC的平行线交AE的延长线于点M,所以∆ABD∆AFM,∆DEC∆MEF.因为所以因为BD=DC,所以故有求得.

图8

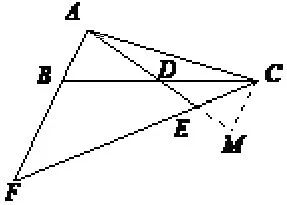
图9

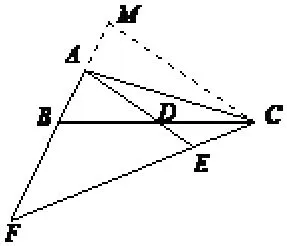
图10

探索五:从点C作平行线

解法九:(如图9) 过点C作AF的平行线交AE的延长线于点M,因为BD=DC,所以∆AEF∆MCE,∆ADB∆MDC.因 为所以有且CM=AB,故有.

(如图10,过点C作AE的平行线交FA的延长线于点M,该方法无法使条件和所求之间建立联系,无法求出结果,放弃!)

探索六:从点A作平行线

(如图11,过点A作BC的平行线交FC的延长线于点M;如图12,过点A作FC的平行线交CB的延长线于点M;该两方法均无法使条件和所求之间建立联系,无法求出结果,放弃!)

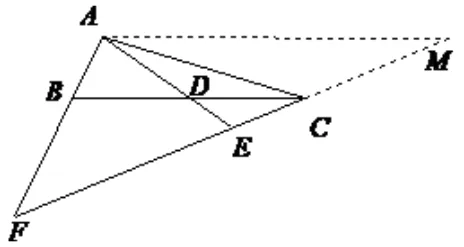
图11

图12

探索七:融合发现

解法十:(如图13,解法三的伴生方法) 过点D作AF的平行线交CF于点M,连接BM,因为BD=DC,所以CM=MF,又因为所以ME=CE,所以三角形CBM中,DE为中位线,所以BM//DE,即BM//AE,所以.

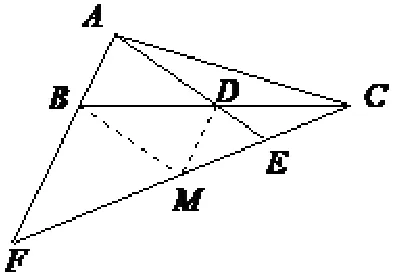
图13

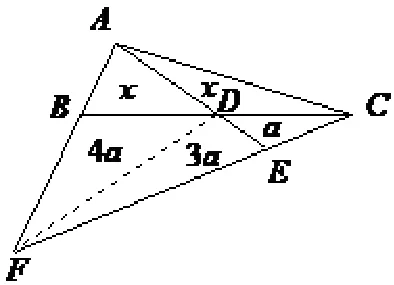
图14

解法十一:(如图14,面积法) 连接DF,因为CE=所以EF=3CE,设∆DEC的面积为a,则∆DEF的面积为3a,因为BD=DC,所以∆DBF的面积等于∆DCF的面积为4a,∆ABD与∆ADC面积相等设为x,则∆AEF的面积为∆AEC面积的3 倍,即7a+x=3(a+x),求得x=2a,所以.

作出辅助线,本身就是一个“创造”(因为原来没有),关键是在哪儿作,怎么作?上述过程对各种可能的情形都进行了探索,有的成功有的失败.探究的过程使学生获得了经验与方法,知道了怎么作是有效的.学生增长了动手实验的能力和体验,增强了思维能力.