多角度纤维缠绕复合材料圆筒张力设计①

郭凯特，文立华 ，校金友，张承双，李正道

(1.西北工业大学 航天学院，西安 710072；2.中国航天科技集团有限公司四院四十三所，西安 710025)

0 引言

纤维增强复合材料圆筒因其高的比强度、比模量、轻量化和腐蚀阻抗等优越性能，被广泛用于航空航天和石油化工等领域[1-2]。如何确定纤维缠绕复合材料圆筒的设计参数(纤维体积分数、缠绕角、铺层顺序和张力梯度等)，最大化其刚度强度，最小化其质量，一直是该领域内设计师不断追求的目标。张力设计与控制对于缠绕壳体的成品质量和力学性能有很大的影响[2]。在纤维缠绕过程中，施加张力的主要目的是控制树脂含量和使纤维在芯模上按照规定线型排列，适当和平稳的张力可以增强构件承受内压的能力，提高其抗疲劳特性，张力太大有可能造成纤维磨损严重，内层含胶量偏低，进而影响纤维缠绕构件的承载能力[3]。

关于复合材料圆筒生产过程工艺参数对缠绕构件力学性能的影响机理方面，许多学者进行了探索研究。早期一些学者采用有限差分法和其他数值方法研究了固化过程中的张力诱导应力[5-7]。为更加准确确定复合材料圆筒残余应力，一些学者考虑了缠绕张力和固化过程中的参数的耦合效应，以求获得更加准确的残余应力[8-11]。Cohen[3]采用实验的方法研究了缠绕张力对于壳体力学性能的影响，发现缠绕张力是最重要的影响因素，适当地增加缠绕张力，会导致缠绕构件具有更高的纤维体积份数，进而提高缠绕结构件的承载能力。随后，Cohen[4]又进一步研究了纤维体积分数与纤维缠绕压力容器与失效强度的关系。Xia[12]基于各向异性弹性力学，提出了一种计算多层纤维缠绕管在内压作用下应力应变位移的解析计算方法，为采用解析方法研究缠绕参数对复合材料圆筒力学性能影响奠定了基础。Rousseau[13]研究了螺旋缠绕情况下纤维重叠程度对于纤维缠绕圆筒力学性能的影响规律，发现纤维重叠交织越严重，在内压作用下，损伤就越容易产生，进而影响结构件的力学性能。Mertiny[14]采用实验的方法研究了铺层顺序多层复合材料圆筒在双轴载荷作用下力学性能的影响。Fernand[15]采用实验的方法研究了复合材料圆筒在不同温度下水分的吸收对于缠绕构件力学性能的影响，他们发现随着结构水分的吸收，复合材料圆筒的强度和刚度均在下降。然而，上述研究主要采用实验的方法取探究工艺参数对缠绕构件力学性能的影响规律，而且对于张力对复合材料圆筒力学性能的影响仅限于常张力情况。

针对纯环向缠绕的厚壁复合材料圆筒，Kang[16]采用解析分析的方法，获得环向缠绕下生产工艺参数对于复合材料圆筒残余应力的影响，他们考虑了缠绕张力、固化过程中热应力和固化收缩应力对于构件残余应力的影响，并进行了实验验证，获得了令人满意的结果。Garret[17]采用实验的方法获得±60°复合材料玻璃纤维增强树脂基圆管在双轴载荷下的失效包线，他们测试了14组双轴应力比下的失效应力应变，总结了5种典型失效模式，对于在双轴载荷下复合材料圆筒的设计有一定指导意义。

丁宝庚等考虑了纤维束缠绕张力对已缠绕层的“放松效应”及缠绕张力引起的内衬弯曲变形，建立了具有薄壁金属内衬的缠绕张力公式[18]。吴德会[19]采用神经网络算法，提出了一种针对纯环向缠绕的厚壁复合材料缠绕张力的设计方法，并通过实验验证了该方法的有效性。邢静忠等[20-22]根据各向同性材料三维本构关系，考虑环向缠绕张力对已缠绕层张力产生的放松量，建立了环向缠绕张力与缠绕后剩余张力分布关系，提出了给定剩余张力分布计算缠绕张力变化规律的计算方法。苏维国等[23]通过研究发现，对于纯环向缠绕的复合材料圆筒，发现纤维张力缠绕中预应力的饱和现象，并确定了影响张力缠绕预应力场的两个主要参数，缠绕层环径向刚度比和张力大小，为复合材料环向缠绕成型工艺提供理论支撑。肖宏成等[24]基于生死单元及多步连续降温，给出了纤维缠绕增强复合材料身管的预应力逐层模拟方法。李博等[25]基于正交各向异性材料的厚壁圆筒理论和弹性叠加理论，提出了考虑卸去芯模影响的多角度交替缠绕下剩余应力算法，并基于等应力假设，初步优化了适用于内压管的张力。

虽然前人对于纤维增强树脂基复合材料圆筒缠绕张力、缠绕角、铺层顺序和固化过程工艺对于其力学性能影响机理进行了相关研究，然而对于张力的研究主要集中在采用实验方法研究其对于复合材料圆筒的力学性能，采用解析分析模型研究张力对于复合材料圆筒残余应力的影响也仅仅考虑了纯环向缠绕的情况。本文基于3维各向异性弹性力学，提出了一种针对任意缠绕形式的多层复合材料纤维增强树脂基圆筒的张力设计方法。模型中采用叠加原理获得任意缠绕张力梯度下圆筒的残余应力，针对任意铺层形式，采用Tsai-Wu失效准则获得了使得爆破压强最大的缠绕张力，对优化结果进行了分析讨论，对纤维缠绕圆筒张力设计具有一定的实际指导意义。

1 考虑张力的多角度纤维缠绕复合材料圆筒解析分析模型

图1为多层复合材料圆筒缠绕模型，CFRP缠绕层由螺旋缠绕和环向缠绕组成。复合材料圆筒内径为R0，纤维缠绕了n层之后外径为Rn，总厚度为tn，第j层的半径为Rj=R0+j×t，其中t为复合材料单层厚度。材料坐标系1方向为纤维方向，2方向为层内垂直于纤维方向，3方向垂直于12平面指向圆筒外侧。第j层纤维束缠绕张力为Fj，环向缠绕90°，螺旋缠绕±α。

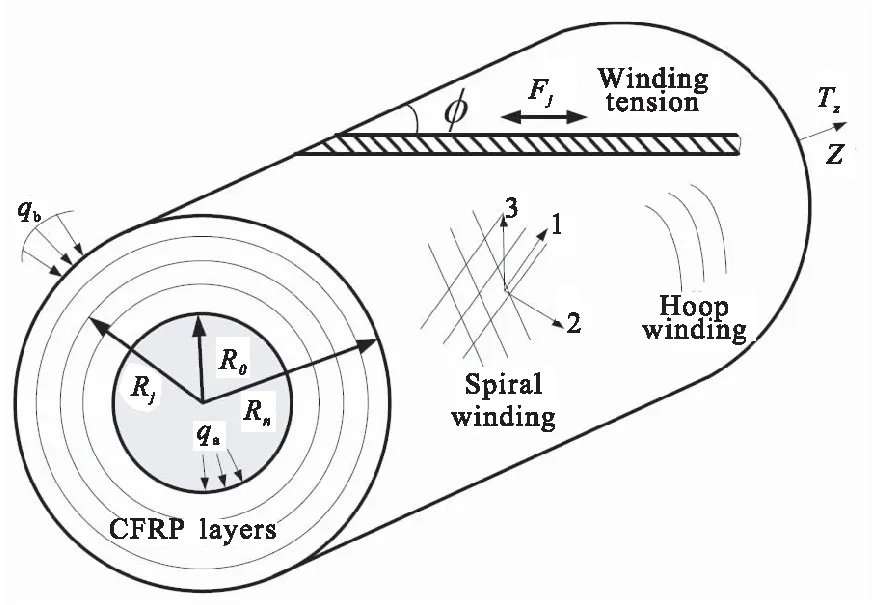
图1 多层复合材料缠绕圆筒模型Fig.1 Geometric model of multi-sequence composite cylinder

计算多层复合材料圆筒应力应变时基于以下假设：(1)由于复合材料破坏属于准脆性材料，因此假设复合材料圆筒破坏前均处于弹性阶段；(2)由于在缠绕过程中张力始终处于较小的水平，因此假设张力诱导的复合材料圆筒残余应力均处于线弹性阶段，满足叠加原理；(3)由于缠绕张力较小，因此模型中忽略张力导致的复合材料层的半径变化；(4)假设缠绕后复合材料层为标准的圆柱筒形，各层之间连接紧密。

1.1 复合材料缠绕层应力分析

针对图1所示的多层复合材料缠绕圆筒模型，圆柱坐标系下,z、r和θ分别代表轴向、径向和环向。内压为qa，外压为qb，轴向载荷为Tz。在这3种载荷作用下，圆筒内部仅会产生径向位移和轴向位移。ur、uθ和uz分别代表圆筒的径向位移、环向位移和轴向位移，对于第i个纤维层而言，几何关系如下：

(1)

第i层平衡方程如下：

(2)

(3)

=[S]{σ}

(4)

式中E1、E2和E3分别为材料坐标系下的弹性模量；ν12、ν13和ν23分别为12平面、13平面和23平面泊松比；G12、G13和G23分别为12平面、13平面和23平面泊剪切模量。

材料坐标系应变与柱坐标系应变转换矩阵[Tε]：

(5)

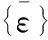
材料坐标系应力与柱坐标系应力转换矩阵[Tσ]：

(6)

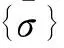
柱坐标系下的柔度矩阵：

(7)

柱坐标系下刚度矩阵：

(8)

第i个铺层柱坐标系下的应力-应变关系：

(9)

结合式(1)，将式(9)代入式(2)，可得

(10)

该方程通解为

(11)

结合式(11)、式(10)和式(1)，可得

(12)

(13)

式(14)～式(16)结合式(11)，可得柱坐标系下的径向位移场，当柱坐标系下位移计算出来后，根据式(5)和式(7)，可获得材料坐标系下的应力和应变。

铺层之间的位移与应力连续：

(14)

轴向平衡方程：

(15)

1.2 张力诱导多层复合材料圆筒残余应力分析

纤维缠绕复合材料管由多层连续纤维束缠绕在芯模上固化而成。由于缠绕张力的存在，会引起复合材料芯模与当前缠绕层之间的相互作用，这种作用类似于薄套筒与芯模之间的过盈配合的作用。在纤维束缠绕过程中，每在最外层缠绕一层纤维构成一个复合材料的薄套筒，都会对已经存在的复合材料层产生径向压力，导致内部各层产生应力。如图2所示，复合材料已经缠绕至第j层，此时复合芯模的半径已经达到Rj。由于纤维缠绕张紧力Fj的作用，最外层纤维构成的薄套筒会对内部复合芯模表面形成一个均匀的外压Pj，在外压的作用下，复合芯模会产生径向形变，从而会对内部各个纤维层产生松弛作用，进而影响内部各层的应力。由于在纤维缠绕过程中张力均控制在材料的线弹性范围内，因此根据弹性力学叠加原理，最终由于纤维缠绕张力导致的复合材料纤维缠绕圆筒各个层的应力应变可以通过第j层到第n层的张力对内层产生的应力应变叠加得到。

图2 纤维缠绕圆筒压强作用示意图Fig.2 Schematic diagram of compaction during filament winding process

1.1节给出了纤维缠绕圆筒在内压、外压和轴向载荷共同作用下的全局坐标系下的应力应变和铺层坐标系下的应力应变分析模型。当纤维缠绕到第j层时，可将该层产生的外压Pj当成第1层至第j-1层构成的圆筒的外压，应用1.1节的分析模型，可计算出第j层对内层产生的应力应变，此时模型需要做相应的调整。

当纤维缠绕至第j层时，认为该层仅对该层纤维方向产生拉应力，该层由于张力产生的压强作为第1层至第j-1层构成的复合材料套筒的外压，该层纤维方向的应力为

(16)

式中b为纱片宽度；t为纱片厚度。

此时，内层纤维应力可写成

(17)

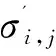
同理，由于张力导致的变形处于线弹性范围之内，第j层的应变可写成

(18)

式中E1为纤维束纤维方向的弹性模量。

内层纤维各个方向的应变可写成

(19)

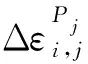
采用第1.1节的方法求解第j层由于张力导致的压强对内部各层的应力应变时，边界条件如下：

(1)认为缠绕内层芯模是刚性模具，因此在芯模表面，可近似认为复合材料层径向位移为0，即

(20)

(2)当纤维缠绕到第j层时，认为第j-1层外表面径向应力大小与Pj相等，即

(21)

(3)由于轴线方向没有作用力，因此有

(22)

(4)纤维层径向应力连续，径向位移连续，可得

(23)

将以上边界条件组合成一个方程组，可写成

[K]{δ}={q}

(24)

其中,{δ}为

{q}={0,-Pj,0,…,0}

(25)

其中，Pj为第j层的张力产生的压强，其计算方法如下：

(26)

其中，Rn为缠绕到第j层时，纤维轨迹上某一点的法向曲率半径，由微分几何理论可知：

(27)

对于筒身段而言，r=Rj-1，r' =0,r"=0,结合式(27)，可得

(28)

将式(28)代入式(26)，可得由于第j层张力作用导致的压强为

(29)

结合式(29)求解式(24)，可得每一层积分常数和纤维方向的应变。结合式(17)和式(19)，进而可得张力导致的残余应力。将该张力导致的残余应力作为初始应力，圆筒在内压作用下的应力为纯内压作用下的应力与张力导致的残余应力之和，进而可做相应的分析。

1.3 多层复合材料圆筒失效分析

采用宏观失效准则Tsai-Wu来计算纤维缠绕圆筒的极限爆破内压。Tsai-Wu失效准则表达式如下：

(30)

式中σ1、σ、τ12分别为面内纤维方向的应力、面内垂直于纤维方向的应力和面内剪切应力；Xs、Xc、Ys、Yc、S分别为沿纤维方向的拉伸强度、沿纤维方向的压缩强度、垂直于纤维方向的拉伸强度、垂直于纤维方向的压缩强度和面内剪切强度。

一般来说，在外载荷作用下，3个应力分量往往按照一定的比例增加。因此，可将它们表示成某一待定应力的函数，代入到失效准则后，就可以将失效准则转化为一元二次方程，从而确定这个函数。定义的某一分量应力极限值与其对应的应力的比值为强度比，记为R，即

R=σi(a)/σi

(31)

由强度比的定义可知，当作用的应力为0时，R为无穷大；当作用应力小于极限值时，R>1；这时单向板不失效。因此，R代表了安全裕度，如R=2意味着作用应力需要增加1倍才会达到极限值；当作用应力等于极限值时，R=1，可认为材料发生了破坏；当R<1时，表明材料已经失效，没有实际的意义。将式(31)代入式(30)，可得

(32)

其中，

(33)

式(33)中各个系数为

Fzz=1/(XtXc),Frr=1/(YtYc)

Frθ=1/(2YtYc),Fr=1/Yt+1/Yc

Fz=1/Xt+1/Xc

2 多层复合材料圆筒的失效计算流程

图3为多层复合材料圆筒失效分析流程图。

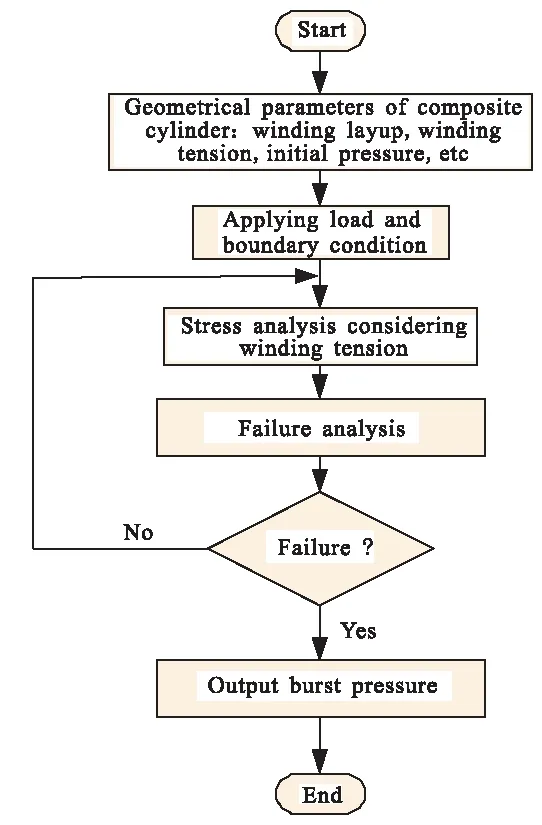
图3 多层复合材料圆筒失效分析Fig.3 Failure analysis of multi-sequence composite cylinder

在给定复合材料圆筒的几何参数以及力学性能参数的情况下，采用本文所提出的方法计算张力和内压共同作用下纤维的应力，结合失效准则获得爆破压强。该分析过程未考虑复合材料圆筒的渐进损伤，因为即使复合材料某一层发生损伤之后，由于应力的重新分配，该复合材料圆筒还可继续承载内压，直到最终破坏，因此采用初始失效准则计算的爆破内压比较保守，但采用初始失效准则计算爆破内压对张力的优化分析结果影响并不大。

3 分析与讨论

3.1 模型的对比验证

图4给出了不同单层厚度下纤维方向应力本文方法与Wu’s方法对比，圆筒内径为50 mm，环向缠绕10层，恒张力40 N缠绕，纱片宽度为3 mm，材料性能参数如表1所示[22]。针对纯环向缠绕，Wu[20]提出了一种计算厚壁纤维缠绕管张力的设计方法，其纤维方向的应力为

(34)

式中F为纤维张力；t为纤维束厚度；h为纤维束宽度；α为缠绕角；R为内径；Rn为外径；μ为平均泊松比。

由图4(a)、(b)可见，当纤维厚度小于1 mm时，两种方法吻合的很好，两种方法误差较大的地方在内径处，这与该模型中芯模的刚性假设有关。对于Wu的方法来说，在各种单层厚度下，纤维应力随着半径的增加均单调增加。当单层厚度比较小的时候，采用本文的方法计算出的纤维应力随着圆筒半径的增加而增加，当单层厚度比较大的时候，纤维方向的应力随着圆筒半径的增加先增加后减小。

(a)t=0.2 mm (b)t=1 mm (c)t=5 mm图4 不同单层厚度下纤维方向张力诱导残余应力对比Fig.4 Comparative study of residual stress with different ply thickness

由图4可知，当单层厚度为0.2 mm时，在圆筒内壁，本文方法计算的残余应力为66 MPa，Wu的方法计算的残余应力为64 MPa，本文方法所得残余应力比Wu的方法所得的残余应力大3%；当单层厚度为1 mm时，在圆筒内壁，本文方法计算的残余应力为12.6 MPa，Wu的方法计算的残余应力为11 MPa，本文方法所得残余应力比Wu的方法所得的残余应力大14.5%；当单层厚度为5 mm时，在圆筒内壁，本文方法计算的残余应力为2.15 MPa，Wu的方法计算的残余应力为0.81 MPa，本文方法所得残余应力比Wu的方法所得的残余应力大165%。随着单层厚度的增加，在圆筒内壁处，两种方法计算所得的结果误差在增加，但当单层厚度比较小的时候，两种方法计算的结果很接近。

本文主要分析单层厚度比较薄的时候的圆筒张力设计情况，因此采用本文提出的方法具有一定的可信度。

3.2 单层纤维缠绕复合材料圆筒张力设计

图5给出了不同缠绕角度下圆筒爆破内压与张力关系图。圆筒内径为50 mm，螺旋缠绕±α，纱片厚度0.2 mm，纱片宽度3 mm，复合材料性能如表1所示。在不同缠绕角下，圆筒爆破压强均随着缠绕张力的增加而表现为先增加后减小的趋势，这与文献[26-27]试验结果趋势一致，从而在一定程度上验证了本文方法的正确性。当缠绕角为10°时，爆破压强最大值相对于张力为0时的爆破压强增加了5.3%，当缠绕角为55°时，爆破压强最大值相对于张力为0时的爆破压强增加了1.8%，当缠绕角为70°时，爆破压强最大值相对于张力为0时的爆破压强增加了2.5%，当缠绕角为85°时，爆破压强最大值相对于张力为0时的爆破压强增加了3.1%，因此爆破压强的增幅随着缠绕角的增加表现为先减小而后增加的趋势。此外，不同缠绕角下对应的最佳张力值不同，当缠绕角是10°时，最佳张力为130 N，当缠绕角是55°时，最佳张力为75 N，当缠绕角是75°，最佳张力为95 N，当缠绕角为85°，最佳张力为100 N。可看出，随着缠绕角的增加，最佳张力值先减小后增加。

表1 复合材料力学性能Table 1 Mechanical properties of composite

(a)Winding angle∶10° (b)Winding angle∶55°

(c)Winding angle∶70° (d)Winding angle∶85°图5 不同缠绕角下爆破压强与张力的关系Fig.5 Relationship of burst pressure and tension under different winding angles

图6给出了不同缠绕角下强度比沿着圆筒径向分布规律。强度比表示某一应力分量的极限值与其对应的应力的比值，它可用来衡量结构在当前载荷下距离破坏的远近程度，当强度比大于1时，强度比越大，说明结构在该载荷下距离破坏位置越远，当强度比小于1时，此时结构已经破坏。由图6可看出，在各种缠绕角度下，张力等于0对应的强度比曲线始终在最佳张力对应的强度比曲线上方，且两者曲线均大于1。因此，随着内压载荷的继续增加，必然是最有张力的圆筒比张力为0的圆筒后破坏，这也解释了在最佳张力下，为什么圆筒的爆破内压会比张力为0时的圆筒的爆破内压大。

(a)Winding angle∶10° (b)Winding angle∶55°

(c)Winding angle∶70° (d)Winding angle∶85°图6 不同缠绕角下强度比与半径的关系Fig.6 Relationship of strength ratio and radius under different winding angles

图7给出了不同缠绕角下爆破压强增长率柱状图，图8不同缠绕角下爆破压强增长率折线图。可看出，随着缠绕角的增加，爆破压强表现为先增加后减小的趋势，当缠绕角为55°时，爆破压强达到了最大值约为0.4 MPa。随着缠绕角的增加，爆破压强的增幅先减小后增加，当缠绕角为10°时，最佳张力对应的爆破压强相对于张力为0的爆破压强增加了5.3%，当缠绕角为55°时，最佳张力对应的爆破压强相对于张力为0的爆破压强增加了1.8%，说明当圆筒为±α螺旋缠绕时，优化张力对于爆破压强的提升有效果，但提升幅度有限。

图7 不同缠绕角下爆破压强增长率Fig.7 Burst pressure growth rate at different winding angles

图8 不同缠绕角下爆破压强增长率折线图Fig.8 Line chart of burst pressure growth rate at different winding angles

3.3 多层纤维缠绕复合材料圆筒张力设计

图9给出了三种不同铺层模式下复合材料圆筒爆破压强与缠绕角及缠绕张力的关系。圆筒内径为50 mm，纱片厚度0.2 mm，纱片宽度3 mm，复合材料性能如表格1所示。图9(a)铺层模式是±θ，图9(b)铺层模式是[±θ90±θ90]，图9(c)铺层模式是[±θ±θ±θ9090]，缠绕张力为恒张力缠绕，张力变化范围是0～300 N。这里恒张力缠绕指的是每一层缠绕张力均相同，没有张力递减。一般来讲，为了更好发挥复合材料力学性能，工程上都会用张力递减的方法进行缠绕，然而本文研究的重点在于缠绕张力大小对壳体强度的影响规律，而且本文研究的缠绕壳体厚度与半径最大值比小于0.032，属于薄壳范畴，因此暂不考虑张力递减规律。具体缠绕时张力如何递减才能获得更大的纤维强度发挥率需要进一步研究。

由图9可看出，在不同铺层模式和不同张力值下，爆破压强均在55°左右达到最大值。铺层模式一定张力一定的情况下，爆破压强均随着缠绕角的增加先增加后减小，当铺层模式确定的情况下，爆破压强随着缠绕张力的增加先增加后减小。这也是不难理解的，当张力比较小时，随着张力的适当增加，各种纤维之间紧密结合，有助于提升复合材料圆筒承受内压的能力，随着张力的进一步增加，纤维由于张力导致的残余应力会迅速增加，因此在结构件还没有承受内压时，纤维就已经承受了比较大的预紧力，复合材料圆筒的爆破内压反而还会下降。因此，对于给定铺层模式，需要合理确定其缠绕张力，以保证最大限度地发挥纤维的承载能力。

(a)±θ (b)[±θ90±θ/90] (c)[±θ±θ±θ9090]图9 多层复合材料爆破压强与缠绕角及缠绕张力关系Fig.9 Relationship between burst pressure of multisequence composite cylinder and winding angle and winding tension

4 结论

(1)针对多层复合材料圆筒，基于厚壁复合材料圆筒3维解析应力应变分析方法，结合缠绕张力较小进而导致应力应变较小的特点，采用线性叠加原理，建立了多层纤维缠绕复合材料圆筒张力诱导残余应力解析分析模型，通过与前人模型计算结果的对比，获得了令人满意的精度，验证了模型的正确性。

(2)基于提出的张力诱导残余应力模型，将张力诱导残余应力作为复合材料缠绕层初始应力，在内压作用下的应力为纯内压应力与张力诱导残余应力之和，基于Tsai-Wu失效准则，建立了多层纤维缠绕复合材料圆筒张力优化方法。

(3) 对于单层螺旋缠绕，当缠绕角一定的情况下，随着张力的增加，圆筒爆破内压先增加后减小。不同缠绕角下对应的最佳张力值不同，随着缠绕角从0°～90°的增加，最佳张力值先减小后增加。

(4) 对于多层螺旋缠绕，铺层模式一定、张力一定的情况下，随着缠绕角的增加，爆破压强均先增加后减小，当铺层模式确定的情况，随着缠绕张力的增加，爆破压强先增加后减小。因此，对于给定铺层模式，需要合理确定其缠绕张力，以保证最大限度地发挥纤维的承载能力。