基于OpenFOAM平台的钝体稳焰器尾流动力学分析①

王 祎，吴宝元

(1.液体火箭发动机技术重点实验室 西安航天动力研究所，西安 710100；2.航天推进技术研究院，西安 710100)

0 引言

由于固体冲压发动机燃烧室等多种吸气式发动机燃烧室入口来流流速远高于火焰传播速度，在不采取任何措施的情况下无法组织稳定燃烧，因此需要采用合理的火焰稳定手段使燃烧室能够稳定工作[1-2]。

钝体稳焰器作为一种结构简单、性能稳定的火焰稳定装置得到了广泛应用[3]。其通过在下游产生局部低速尾流形成稳定持续的点燃烧条件，使燃烧室能够稳定工作。钝体稳焰器属于典型的钝体结构，其流场下游尾流低速区与高速主流之间存在不稳定的剪切层，具有本质非稳定特性[4-6]。同时，钝体稳焰器尾流流场包含不同尺度的三维非定常涡结构，对流体动力学分析提出了较大的挑战。

计算流体力学方法(CFD)具备对非定常流场进行精细定量求解的能力，能够满足钝体稳焰器非定常流动研究需求，逐渐成为钝体稳焰器流动研究的重要方法。从不同的研究目的出发，基于CFD方法的数值研究可大致分为钝体稳焰器冷态流场研究[7-9]与燃烧场研究[10-11]。这些研究工作均需要以选取合理的湍流模拟方法为基础获取合理的钝体稳焰器非定常尾流流场流动特征。

已有研究结果表明，传统的雷诺平均湍流模拟方法(RANS)不适用于此类大范围分离流动问题，需要采用合理的尺度解析湍流模拟方法(SRS)或者大涡模拟方法(LES)[12-13]。另一方面，考虑到壁面直接解析的大涡模拟方法在壁面附近的网格要求与直接模拟方法(DNS)相似，对计算要求较高，壁面模化的大涡模拟方法(WMLES)依然对近壁面网格有较高要求。基于分离涡思想发展而来的DES类方法则充分结合了RANS在近壁面网格处理方面的优势与LES对自由剪切流动的解析能力，较好的平衡了计算效率与计算精度之间的矛盾，是一种适用于研究钝体稳焰器尾流流动的湍流模拟方法。

获取合理的非定常尾流流场计算结果的同时，钝体稳焰器研究需采用合理的后处理手段对尾流动力学特性进行分析。传统方法往往通过对钝体稳焰器升阻力系数或尾流监测点速度压力等物理量进行快速傅里叶变换获取动力学特征频率，但此类方法很难表征整个流场的动力学特征[14]。近年来以本征正交分解方法(POD)[15]以及动力学模态分解方法(DMD)[16]为代表的流场降维分析方法以非定常流场切片为输入能够充分考虑整个流场信息，能够获取更加丰富的流场动力学特征，是分析钝体稳焰器尾流非定常流动问题一种很有潜力的方法。

本文选取Sjunnesson等[17]开展的Volvo试验为基本构型，基于OpenFOAM开源计算力体力学平台[18]，采用改进延迟分离涡湍流模拟方法(IDDES)对其冷态试验工况进行仿真计算。针对复杂的尾流涡结构，采取Omega涡识别方法对动态涡结构进行识别；进一步采用动力学模态分解方法提取流场主要特征，对尾流流体动力学特性进行详细分析。

1 计算模型

Volvo流动试验为Sjunnesson等[17]于1992年公开的的针对钝体稳焰器开展的试验研究，具有较详细的冷热态试验结果。试验结构可以简化抽象为包含三棱柱钝体稳焰器的长方体展向流场结构，具体钝体稳焰器及流场结构尺寸如图1所示。

图1 Volvo试验结构示意图Fig.1 Volvo rig case configuration

钝体稳焰器为横切面为等边三角形的实心三棱柱结构，另外由上下两实体面确定流场范围。展向抽象为无限长，仅截取部分展向长度，并通过周期性边界进行模化。根据冷态试验条件可以获得详细的计算物理模型边界条件，见表1。

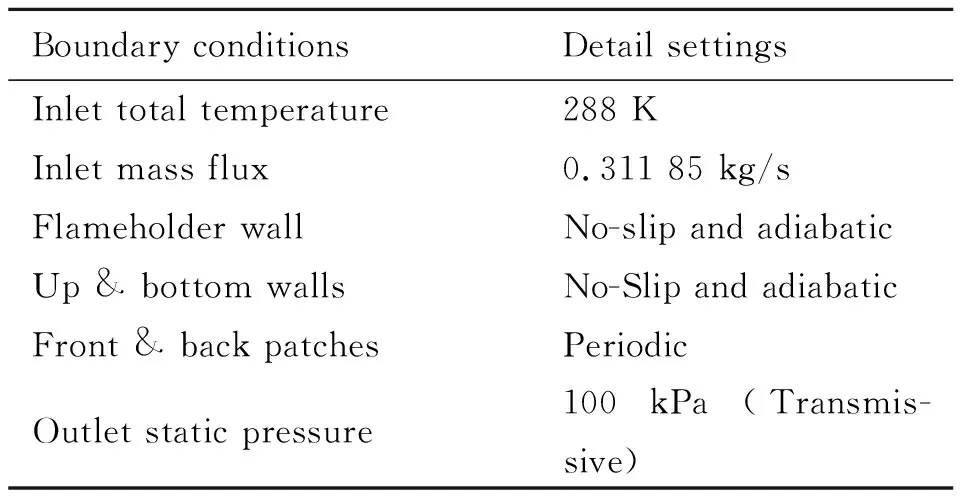
表1 冷态试验具体边界条件Table 1 Cold state boundary conditions

本文采用六面体网格对流场计算域进行网格划分，对近壁面以及剪切层附近网格局部加密以满足湍流模拟要求，保证壁面第一层网格特征高度y+<10，同时采用自适应的壁面函数，防止非定常计算过程中局部流场流速变化导致的y+变化。展向包含50层网格，整个计算域共划分约140万网格，具体展向横切面网格如图2所示。

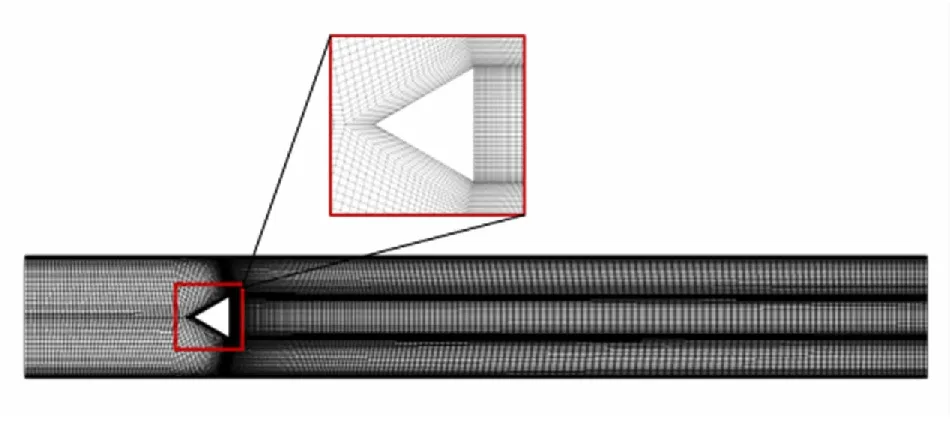
图2 展向横切面网格Fig.2 Grid of the channel plane

参考Sjunnesson等[17]开展的试验，流场中流体工质为当量比为0.65的丙烷/空气预混气体。由于只考虑冷流情况，可将匀混气体作为符合理想气体状态方程的均匀混合物，具体热物性设置见图3。

图3 热物性具体设置Fig.3 The detailed thermo properties

2 数值模拟方法

2.1 大范围分离流动模拟方法

本文基于OpenFOAM开源计算流体力学仿真平台，对Volvo钝体稳焰器冷态流场进行数值仿真。选取基于κ-ωSST的改进延迟分离涡湍流模型(IDDES)以满足大范围分离流动仿真要求。湍流模型具体为

(1)

ρβω2-ρ(F1-1)CDkω+Sω

(2)

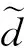
(3)

由于湍流粘性由湍流模型提供，因此选取时间空间离散方法时除了保证数值稳定性以外，需要考虑数值粘性，以免得到非物理结果。参考相关文献，综合考虑稳定性与数值粘性，空间离散格式选取二阶中心有界差分格式，时间离散格式选取二阶隐式backward格式。同时选取压力基PISO迭代方法以进一步减小非定常数值模拟中的数值粘性[20]。选取非定常时间步长为2.0×10-6以满足CFL数小于1，并选取仿真物理时间为1 s。

2.2 Omega涡识别方法

钝体稳焰器尾流流场包含复杂的三维涡结构，需选取合理的涡识别方法用于对其进行识别分析。Omega涡识别方法与涡量法以及速度梯度不变量等涡识别方法相比，能够清晰识别不同强度的涡结构，并且具有较为一致的识别标准[21]。该方法通过定义涡识别变量：

(4)

a=tr(ATA)

(5)

b=tr(BTB)

(6)

式中A，B分别为速度梯度的对称张量与反对称张量；ε为一极小值以免出现分母为0，本文选取为0.001；根据相关文献研究结果，选取Ω=0.52等值面作为涡识别判据。

2.3 动力学模态分解方法[22-24]

动力学模态分解方法(DMD)结合了主成分分析(PCA)与傅里叶变换(FT)，可以将含有不同尺度的涡结构分解为不同频率的主模态，有利于在大量的流场数据中提取主要流体动力学特性进行分析研究。

非定常流场作为一个复杂的非线性动力学系统可以通过线性化为时间离散系统：

xk+1=Axk

(7)

式中 下标表示不同时间步。

选取相同时间间隔的m个瞬态流场结果，基于式(7)可以构建如下动力学关系式：

X=[x1x2…xm-1]

(8)

X′=[x2x3…xm]

(9)

X′≈AX

(10)

可以通过奇异值分解(SVD)方法求得系统矩阵的具体形式：

X≈UΣV*

(11)

A=X′VΣU*

(12)

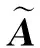
(13)

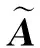
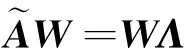
(14)

Φ=X′VΣ-1W

(15)

通过对角矩阵Λ中的离散特征值λk可以构建对应的连续特征值ωk=ln(λk)/Δt，其实数部分表征相应DMD模态的增长率，虚数部分表征相应DMD模态的频率。

定义模态振幅b为不同DMD模态对流场序列X的贡献，即b=Φ/X。进一步可以使用若干个DMD模态对不同时刻流场进行重构或者预测：

x(t)≈ΦeΩtb

(16)

式中Ω为由特征值ωk组成的对角矩阵。

综上，采用DMD方法能够获得具有主成分特征的DMD模态，相较于传统的傅里叶分解方法具有更强的可操作性。通过讨论其连续特征值的性质能够辨别各DMD模态的动力学稳定性，并且可以明确不同频率模态的流动模式，具有较强的物理意义，对于流体动力学分析具有良好的指导意义。

3 计算结果验证及分析

3.1 计算结果验证

通过统计物理时间0.5～1.0 s 内时均速度与速度脉动量与试验结果进行对比，验证计算结果的准确性。

图4为选取流场中轴线上轴向时均速度与试验结果的对比图。除了给出基于κ-ωSST IDDES湍流模型的计算结果外，也给出了基于κ-ωSST非稳态雷诺平均(URANS)湍流模型的计算结果。通过对比可以明显看出，基于URANS湍流模型的计算结果与试验结果相差较大，表明其无法对钝体稳焰器尾流流场进行较合理地预示。其主要原因是κ-ωSST URANS模型基于线性涡黏假设，其中仅考虑了从大尺度涡向小尺度耗散涡能量级串过程，无法解析自由剪切运动中反向级串过程，导致流场自由剪切部分湍流黏性预示过高，低速回流区含能较大，导致对回流区速度预示过高。IDDES湍流模型在近壁面采用RANS模式能够配合合理的壁面函数高效的模化附面层流动；在远离壁面的自由剪切流动切换至适用于自由剪切流的LES模式，对自由剪切流进行合理模化。因此，基于IDDES湍流模型的计算结果与试验结果较为吻合，速度形预示较为准确。

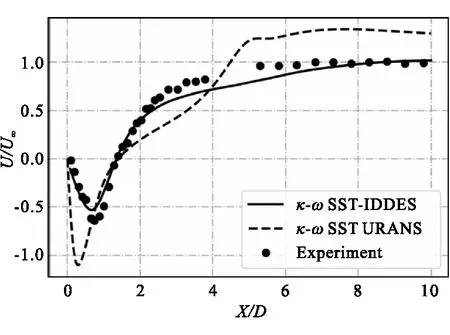
图4 流场中轴线轴向时均速度形Fig.4 Time-average axial velocity profile along the centerline

为进一步验证基于IDDES湍流模型计算结果的准确性，图5与图6分别给出了沿流场中轴线速度脉动量以及不同流场横截面上轴向时均速度形的对比示意图。通过对比分析，表明本文选取求解器、离散格式、流动模型能够对钝体稳焰器尾流流场进行较精确地预示。

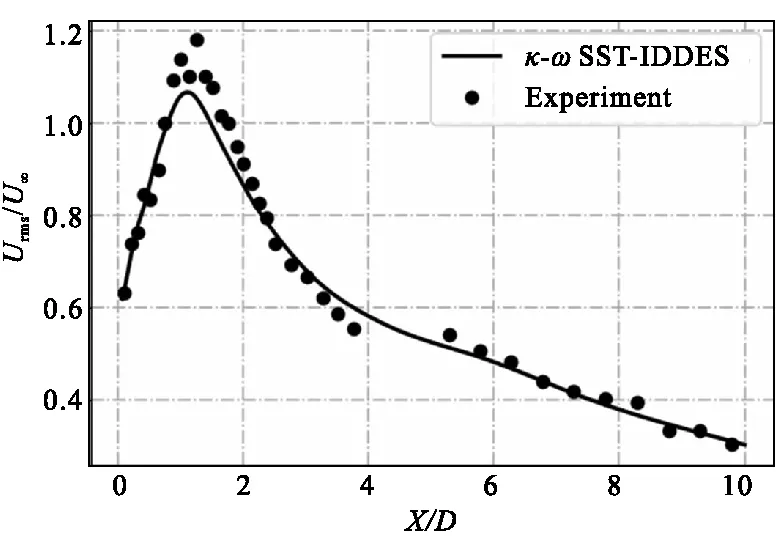
图5 流场中轴线速度脉动量分布图Fig.5 Fluctuation velocity profile along the centerline

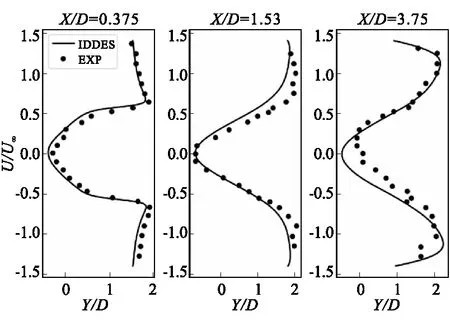
图6 不同流场横截面轴向时均速度形Fig.6 Time-average axial velocity profile at different cross section

3.2 计算结果分析

在计算过程中对非定常计算结果进行时间平均处理可以获得相应物理量的时均值与时间脉动量。3.1节已经将时均化的计算结果与试验结果进行了对比验证，本节进一步给出轴向时均速度分布图，如图7所示。由图可知，高速来流经过钝体稳焰器在下游流场形成了典型的尾流结构；与无限大空间钝体绕流不同的是，由于壁面限制流体在流经钝体稳焰器的过程中流通面积减小，主流速度明显高于入口来流速度。

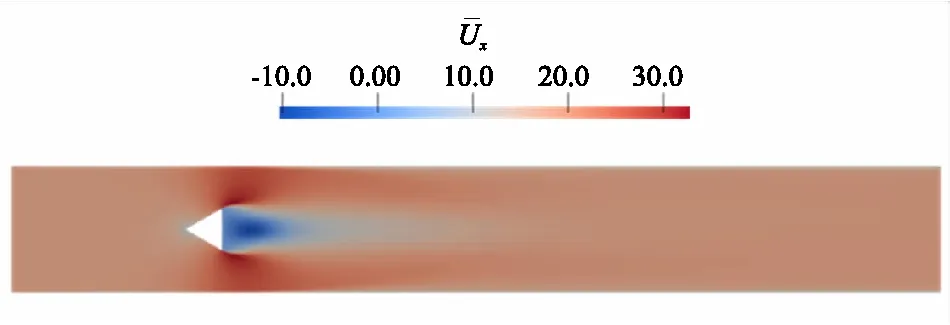
图7 流场轴向时均速度分布图Fig.7 Time-average axial velocity profile of flow field

除可通过时均值获得流场相关物理量的系综平均结果，相关的脉动量能够用于表征流场的非定常特性。图8为流场压强脉动量分布图，由计算结果可得，非定常流动主要集中在钝体稳焰器尾流低速回流区及剪切层部分，且强度沿流向减弱。

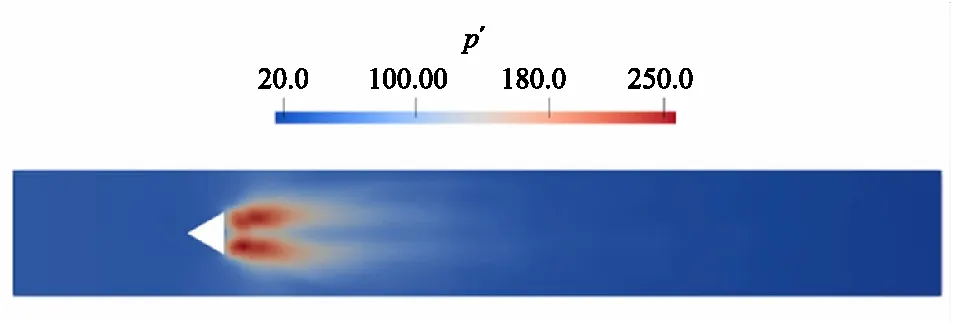
图8 流场压强脉动量分布图Fig.8 Pressure fluctuation profile of flow field

在流场中轴线距稳焰器尾缘0.04 m 下游设置观测点统计其非定常速度值，可通过快速傅里叶变换(FFT)得到单点湍动能随波数的分布图，如图9所示。湍动能分布符合Kolmogorov湍动能 -5/3幂律分布假设[25]，同时存在由尾流非定常涡脱落特征频率为100 Hz左右的分峰值。

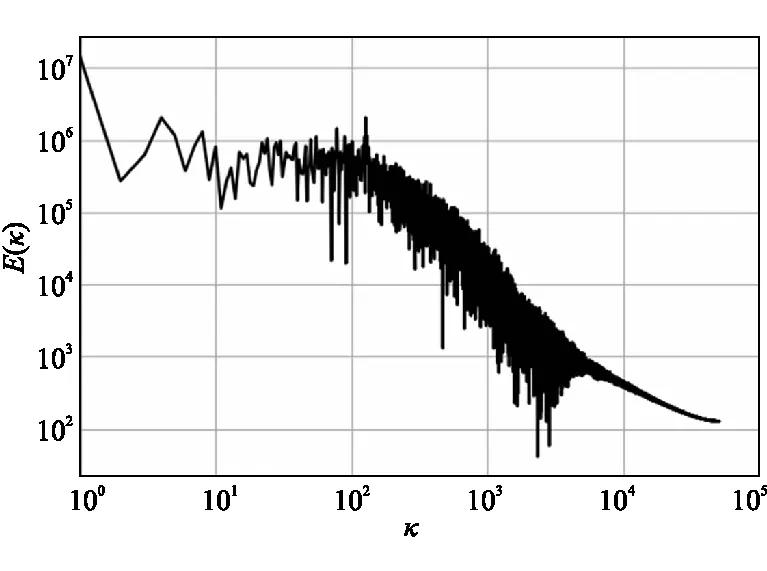
图9 观测点湍流谱分布图Fig.9 Turbulence spectrum of the probe point

与时均化结果不同，瞬态流场包含复杂的三维非定常涡结构。由2.2节，选取单个周期不同时刻流场使用Omega涡识别方法进行处理，可以识别尾流流场中复杂的涡结构。

图10为同一涡脱落周期内不同时刻尾流流场非定常涡结构示意图。由图10可知虽然流场具有准二维几何特征，流体流经钝体稳焰器除存在典型的非定常卡门涡结构，同时尾流涡存在复杂的三维结构。根据湍流理论，尾流复杂的涡结构是由钝体稳焰器迎风面湍流附面层发展而来。湍流结构除沿壁面流向及法向二维平面随时空发展外，同时沿展向发展，最终形成三维流场结构。

图10 同一周期不同时刻涡结构示意图Fig.10 Vortex structure of different moment during one periodic time

3.3 流体动力学分析

由3.2节可知，瞬态尾流流场存在复杂的非定常三维涡结构，使用如单点湍流谱等分析方法很难对整个流场进行动力学分析。本节采用DMD方法对非定常流场计算结果进行处理，对流场进行动力学分析。

选取0.05 s内共50个瞬态流场快照采用DMD方法进行处理，截取前45个流场DMD模态及特征值对流场动力学特性进行讨论。本文以模态振幅b对DMD模态进行排序，可得不同模态振幅分布，如图11所示。

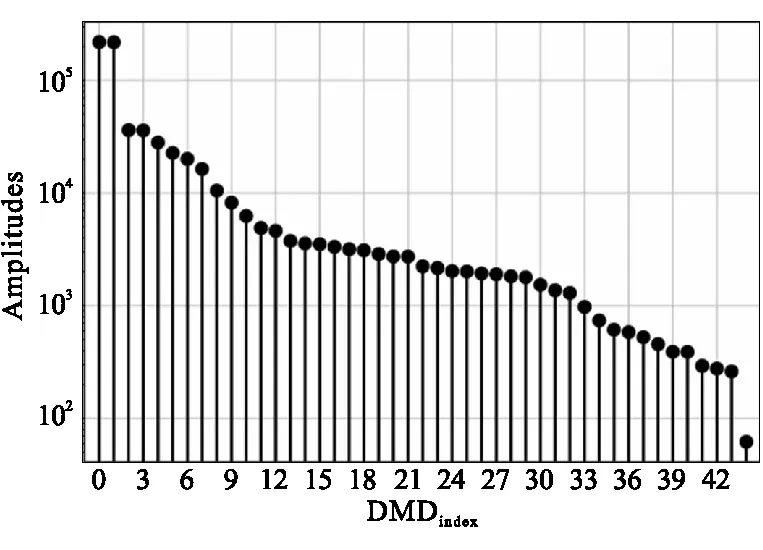
图11 不同DMD模态振幅分布Fig.11 Amplitudes of different DMD modes

根据2.3节，可由离散特征值确定不同DMD模态的稳定性：将复数特征值置于复平面单位圆，若在单位圆内，则相应的DMD模态收敛；在单位圆外，则对应模态发散；在单位圆上，则处于稳定极限环状态。图12为对应不同DMD模态的离散特征值在复平面上的分布。由于截取的瞬态流场经过充分发展已经趋于稳定，同时考虑到流场计算过程中的数值粘性因此各模态离散特征值均处于复平面单位圆内。其中，越接近单位圆，其对应模态稳定性越差，当存在相应频率的流场扰动时相应DMD模态所代表的流动特征越容易被激发为发散状态。本文选取其中10个接近于单位圆的DMD模态进行讨论，如图10中红色特征值所示，同时给出其相应的DMD模态编号。其中，不同DMD模态的特征频率与增长率见表2。由定量数据，除模态5以及模态41以外，其余8个模态为4对共轭模态，10个DMD模态共包含6种不同的特征频率。

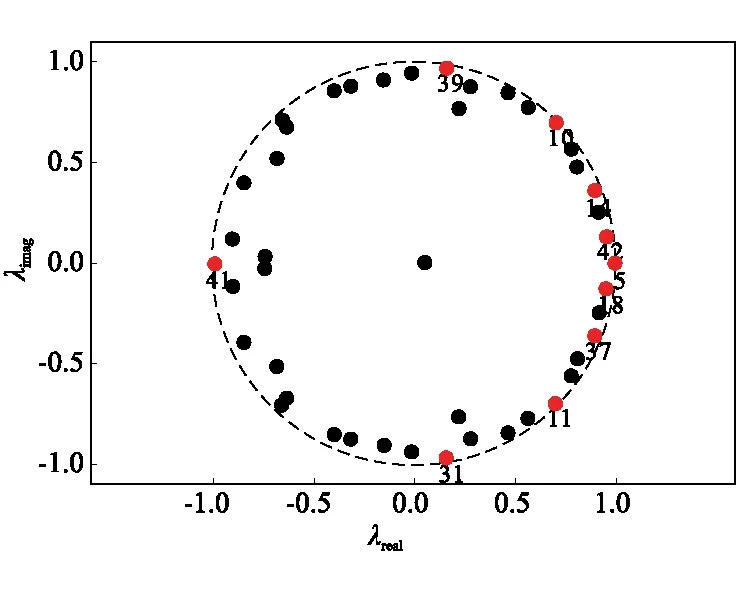
图12 离散特征值分布Fig.12 Discrete eigenvalues of different DMD modes

可以通过DMD模态流向速度分布确定不同模态对应的具体流动特征。根据对比分析可以得出，其中模态5代表尾流稳定低速区流动，其速度云图与图7相似；模态41频率较高，代表流向/横向复合流动特性；模态31与39为一对共轭模态，代表剪切层失稳特性，其频率为剪切层响应频率；剩余模态特征频率分别为剪切层响应频率的1/2，1/4，1/8，即剪切层失稳特性发展成相应的谐波响应流动特性。参照3.2节湍流谱分析结果，卡门涡脱落频率即为剪切层失稳发展形成，其形式对应于模态18与模态42。

图13展示了模式5、模式31、模式18三个DMD模态的流向速度分布。三个DMD模态分别表征了稳态尾流流动、开尔文-亥姆霍兹(KH)不稳定流动以及贝纳德-冯卡门(BVK)不稳定流动[6]。

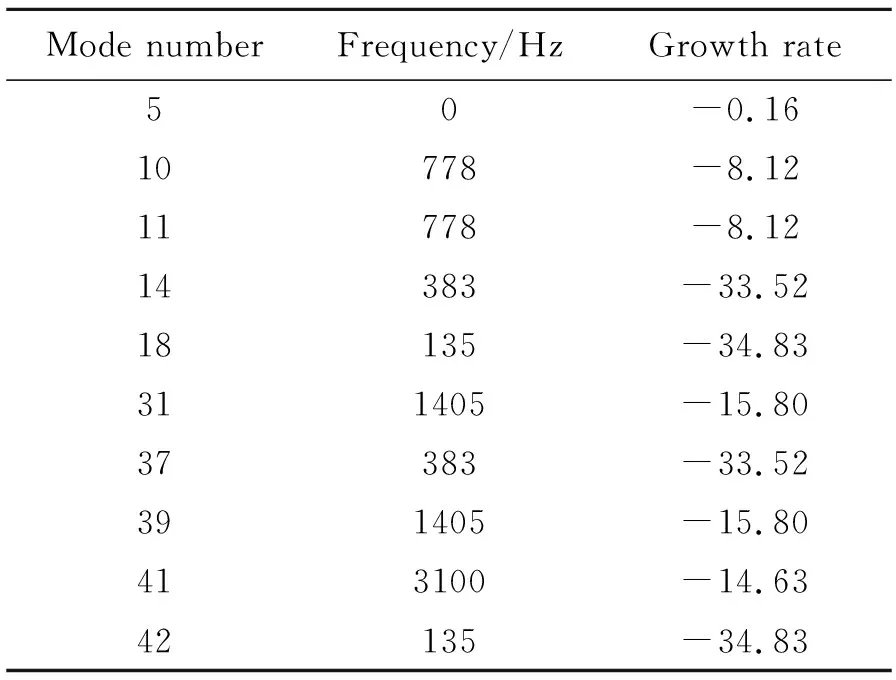
表2 不同DMD模态特征频率与增长率Table 2 Eigenfrequencies and growth rates of different DMD modes

(a) Mode 5

(b) Mode 31

(c) Mode 18图13 部分DMD模态流向速度分布Fig.13 Axial velocity profile of some DMD modes

由图13可知，DMD方法能够获得具有明确物理意义的流体动力学模态，对于钝体稳焰器尾流流动特性的讨论有很大帮助。

另外，表2所示模态基本位于复平面单位圆上，当存在相应特征频率的扰动发生耦合时，相应动力学模态随能量输入有可能演变为不稳定状态，因此需规避相应的特征频率扰动以减小发生流动不稳定的概率。

4 结论

(1)OpenFOAM平台具备开展钝体绕流流动计算仿真的能力。选用的κ-ωSST IDDES湍流模型结合合理的离散格式及边界条件能够获得较为准确的流场计算结果。采用该湍流模拟方法能够兼顾计算效率与计算精度，是一种可用于钝体稳焰器非定常尾流流场仿真计算的高效方法。

(2)Omega涡识别方法能够准确直观展示复杂的涡结构，有助于钝体稳焰器尾流流场分析；与单流场监测点快速傅里叶变换处理获得的湍流能谱分析方法相比，DMD方法可以将非定常流场分解为具有不同特征频率的DMD模态，能够对尾流流场进行细致的流体动力学分析，有利于从整体上把握流场流动特性。

(3)经由本文分析讨论，Volvo冷态试验条件下存在典型的钝体尾流KH不稳定及BVK不稳定流动结构，其流动特征频率分别为1405 Hz、135 Hz。其中，BVK不稳定流动由KH不稳定流动1/8谐波相应发展形成。以上流动模态在存在相应频率扰动时可能会被激发为不稳定流动状态，需在实际工程应用中进行合理规避。