多个洪水共同作用下水利工程防洪标准与重现期

甘富万，黄宇明，张华国，倪倩，肖良*

(1.广西大学土木建筑工程学院，广西南宁530004；2.广西防灾减灾与工程安全重点实验室，广西南宁530004；3.广西珠委南宁勘测设计院，广西南宁530004)

0 引言

重现期的定义为同一个事件前后两次发生的平均间隔时间。重现期是水利工程设计及洪水事件分析中非常重要的概念，同一个洪水事件前后两次发生的平均间隔时间即为洪水重现期[1]。根据《防洪标准(GB 50201—2014)》:“防洪标准是指防护对象防御洪水能力相应的洪水标准；防护对象的防洪标准应以防御的洪水或潮水的重现期表示”[2]。水利工程设计过程中一般以规范规定的设计洪水重现期对应的洪水作为设计洪水，并对设计洪水进行调洪计算得到防洪设计参数[3]。因此，设计洪水重现期是水利工程防洪设计的基本依据，决定了水利工程对洪水防御能力的大小。

对于受单一洪水过程作用的水利工程，由于洪水重现期越大，对应洪水的威胁越大，水利工程防御洪水的能力与设计洪水的重现期总体上具有一一对应性，根据设计洪水重现期易于确定设计洪水及相应防洪设计参数，已有成熟的设计方法。但对于受多个洪水或者洪潮过程共同作用的水利工程，如在江河沿岸的支流入汇口附近修建的防洪排涝闸、堤防等，同时受到内江和外江洪水的共同作用，修建在入海河流(渠道)出口附近的挡潮闸、堤防等，也会同时受到潮水和河流(渠道)洪水的共同作用，这些水利工程的设计洪水必须考虑两个或者多个洪水(包括潮水，下同)的组合情况。针对多个洪水共同作用的水利工程的防洪设计尚无成熟的理论方法，可以采用多变量水文理论进行处理，即在建立两个或多个洪水的联合分布模型的基础上，根据设计洪水重现期计算设计洪水组合，继而确定防洪设计参数。针对单个洪水的峰、量或历时等的研究相对较多[4-6]，而多个洪水共同作用下洪水事件的研究相对较少，由于同一个洪水重现期对应的洪水组合将会有无数个，如何在多变量框架下进行洪水联合设计值估算及风险评估仍然是一个有争议的问题[7-8]。最近有部分学者针对单个洪水作用下设计洪水过程线中洪峰、洪量联合设计值问题提出了基于水工结构安全的两变量洪水重现期，并指出以其进行设计比直接采用传统洪水重现期进行设计更加合理[9-12]，但对多个洪水共同作用的情形，尚未见有相关研究。

本文结合已有相关研究成果，深入探讨了多个洪水共同作用下的设计洪水重现期与水利工程防洪能力的关系，分析了利用设计洪水重现期表示多个洪水共同作用下水利工程防洪标准存在的问题，并提出了更合理的防洪标准表示的方式，为多个洪水共同作用下的水利工程防洪设计提供合理的理论依据和方法。

1 水利工程防洪能力与设计洪水重现期

1.1 单个洪水作用下防洪能力与设计洪水重现期

对于单个洪水的情况，工程设计当中一般采用峰、量同频或者同倍比放大得到设计洪水，或者直接采用洪峰流量作为设计洪水，其本质上是假定洪水重现期越大，洪水量级越大，存在洪水重现期与洪水量级呈正比的关系，如图1所示。相应的，由于洪水量级越大，相应的破坏能力越强，不同洪水重现期与洪水威胁总体上具有一一对应性，且洪水重现期与洪水威胁也同样呈正比的关系。

假定洪水系列为X，x设为设计洪水，T设洪为设计洪水重现期，P为洪水对应的概率，则T设洪=1/P(X>x设)。采用已有成熟的设计洪水计算方法或参考相关规范可容易计算得到频率为P(X>x设)=1/T设洪的设计洪水，将其进行调洪计算即可得到防洪设计水位、防洪库容等相关防洪参数，即f设=f(x设)，这些防洪设计参数f设决定了水利工程防洪能力的大小。T设洪-x设-f设总体上具有一一对应的关系，因此在给定T设洪的条件下进行设计的水利工程的防洪能力具有较好的确定性。

当洪水的重现期T洪大于设计洪水重现期T设洪时，洪水威胁超过设计洪水，相关防洪参数F将超过设计参数f设，水利工程的正常运用将遭到破坏，不考虑设计计算误差，其概率P破坏=P(F>f设)=1/T设洪，水利工程正常运用遭到破坏的平均间隔时间T破坏=1/P破坏=T设洪，即水利工程正常运用遭到破坏的概率与洪水大于设计洪水的概率一致，水利工程正常运用遭到破坏的平均间隔时间与设计洪水重现期T设洪一致，如图2所示。

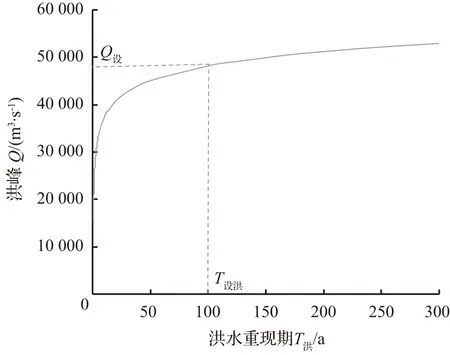
图1 单个洪水情况下洪水重现期与洪水量级关系Fig.1 Relation between flood recurrence period and flood magnitude under single flood condition

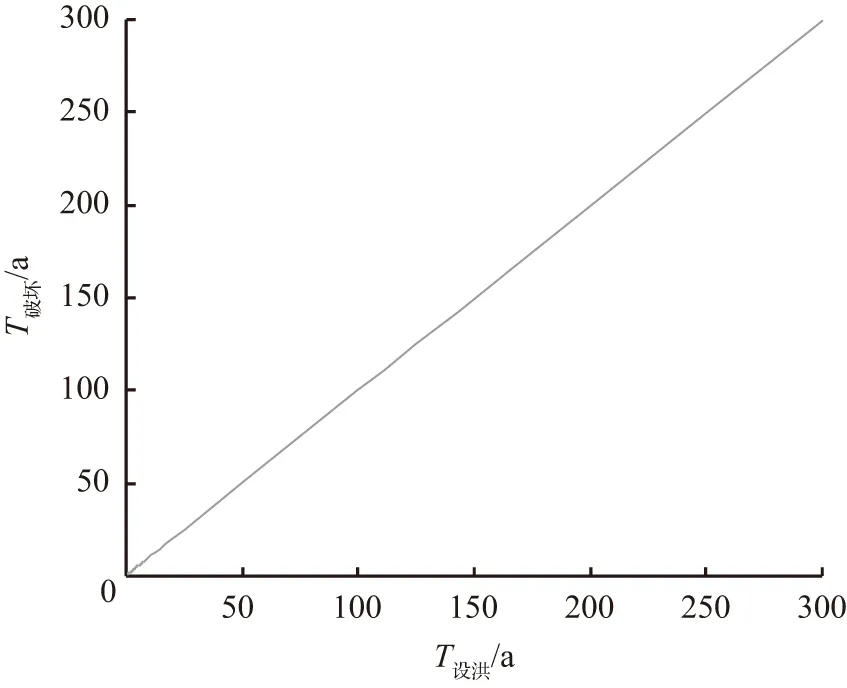
图2 T破坏与T设洪关系Fig.2 Relationship between T破坏 and T设洪

1.2 多个洪水共同作用下防洪能力与设计洪水重现期

在多个洪水共同作用下，设计洪水为多个洪水的组合，必须采用多变量水文理论描述。其传统的洪水重现期有“or”重现期T∨和“and”重现期T∧两种[5]。假定x1、x2、…、xn分别表示洪水事件中具有相依关系的特征变量系列，边缘分布函数为u1=F1(x1)、u2=F2(x2)、…、un=Fn(xn)，C(u1,u2，…,un)为联合分布函数，则“or”重现期和“and”重现期可分别表示为：

(1)

(2)

二维的“or”重现期和“and”重现期可按下式计算：

(3)

(4)

以T∨与T∧作为设计洪水重现期，都存在不同重现期的安全域、危险域交叉的问题，会导致大重现期的危险洪水被小重现期认定为安全洪水，或者小重现期的危险洪水被大重现期认定为安全洪水。

为此，Salvadori等提出了二次重现期Tk的概念[6]，其表达式为：

(5)

以Tk作为设计洪水重现期，其认定的危险域和安全域如图3所示，图中重现期Tk1>Tk2。同一个二次重现期对应的所有洪水组合的危险域完全一致，且大重现期的危险域包含在小重现期的危险域之中，即E1危险⊂E2危险，不会出现大洪水重现期的危险域被小洪水重现期认定为安全域的问题。

目前，三种重现期都在多变量洪水事件中得到了应用[13-15]。然而，利用同一设计洪水重现期进行洪水组合设计时，到底应该采用哪种洪水重现期，尚存在争论。又由于不管是T∨、T∧还是Tk，同一重现期对应无数种洪水组合及无数种可能的威胁，给设计洪水组合的确定带来困难。如图4所示，图中A∨、B∨、C∨、A∧、B∧、C∧、Ak、Bk、Ck分别为同一洪水重现期对应的T∨、T∧、Tk的不同洪水组合，这些洪水组合的洪水重现期全部等于设计洪水重现期，但差别却非常大，以这些洪水组合作为设计洪水组合进行调洪计算得到的防洪参数完全不同，即fA∨≠fB∨≠fC∨≠fA∧≠fB∧≠fC∧≠fAk≠fBk≠fCk，设计得到的水利工程的防洪能力也将完全不同，这必将给水利工程的设计以及运行管理带来巨大的不确定性。

可见，在多个洪水共同作用的情况下，按给定的T设洪进行设计的水利工程的防洪能力不确定，水利工程正常运用遭到破坏的概率P破坏≠1/T设洪，水利工程正常运用遭到破坏的平均间隔时间不确定，且与设计洪水重现期T设洪不一致。

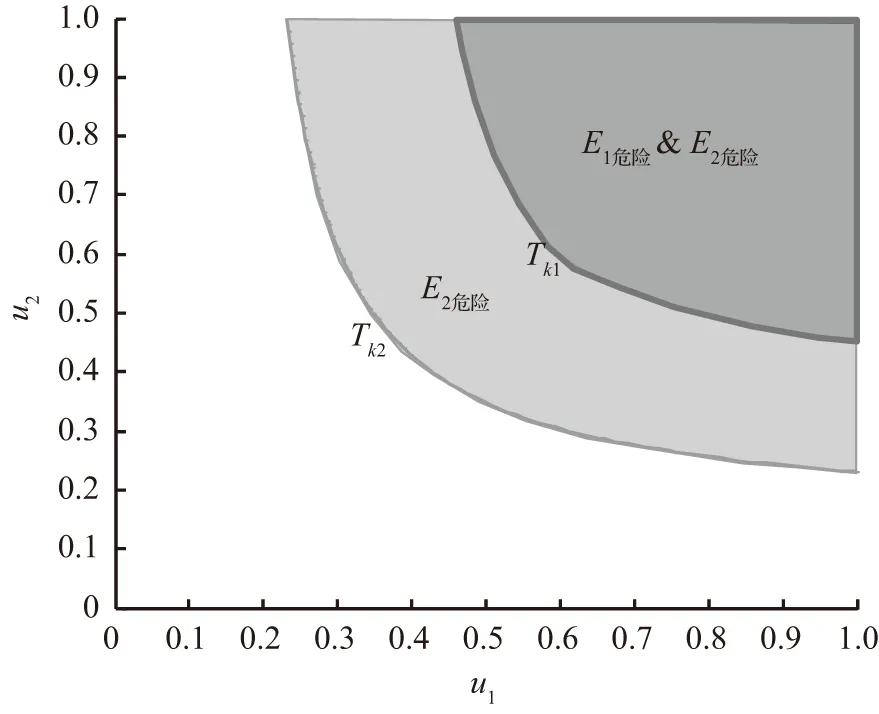
图3 不同二次重现期及其危险域对比Fig.3 Comparison of different secondary recurrence periods and their risk areas

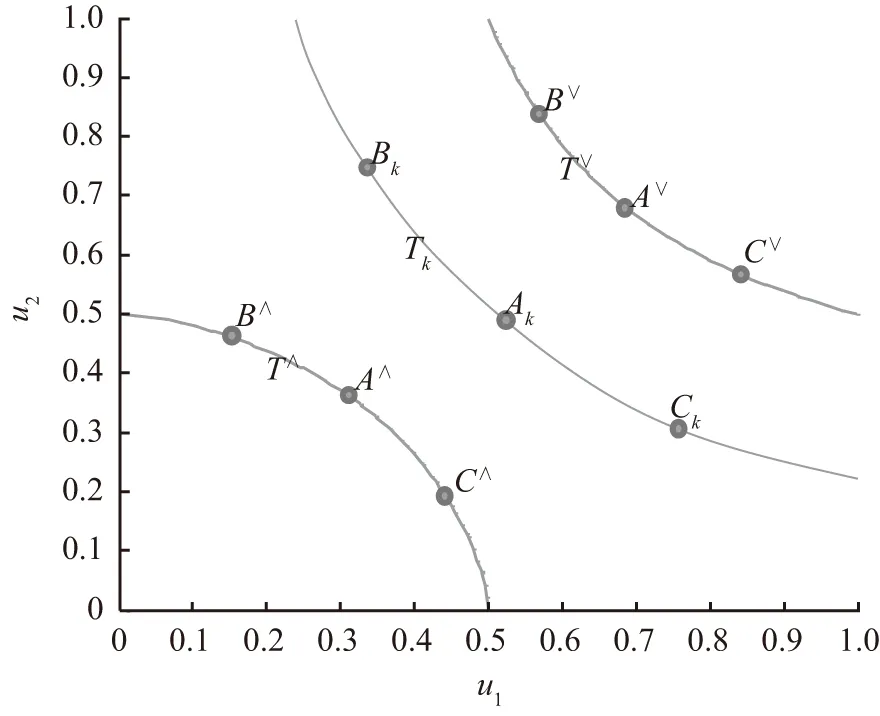
图4 同一设计洪水重现期对应的不同可能设计组合Fig.4 Different possible design combinations corresponding to the same design flood recurrence period

2 多个洪水共同作用下防洪标准的合理表示形式

2.1 基于洪水与行洪边界耦合关系的重现期

防洪设计的目的是保证防护对象具备足够的防洪能力，以保证在洪水破坏力不超过设计的防洪能力的情况下工程的正常运用。在多个洪水共同作用的情况下，防洪重现期的计算一般采用经验组合或者洪水特征组合，缺乏足够的理论依据；而且在实际中，不同行洪边界(包括水利工程和河道特性)对洪水行洪的影响不同，水利工程防洪能力的大小不但与洪水特性有关，也与行洪边界的行洪条件有关。如刘章君等[12]以超过坝前最高水位的频率来度量水库防洪安全设计标准，将洪水作用下超过坝前最高水位的平均间隔时间定义为结构荷载重现期，以其确定的设计洪水过程线考虑了洪峰、洪量与水库调洪规则的交互作用，可达到指定防洪标准，以“or”重现期T∨、“and”重现期T∧、二次重现期Tk等计算得到的防洪设计水位则存在偏高或者偏低的情况。而多个洪水与水利工程的交互作用更加复杂，至于采用何种洪水重现期以及是否需要考虑洪水与行洪边界的耦合关系仍需进行更加严谨的理论分析计算，并结合工程实践才能确定。

为了全面反映多个洪水共同作用下洪水与不同行洪边界的耦合关系，本文以水利工程在正常运用过程中，由于洪水作用导致防洪参数F超过给定值f的平均间隔时间来表示防洪标准，与洪水重现期反映同一个洪水事件前后两次发生的平均间隔时间不同，其反映的是不同防洪参数的值被超过这一事件前后两次发生的平均间隔时间，为了与洪水重现期进行区分，本文将其定义为水利工程的防洪重现期Tf，则：

Tf=1/P(F>f)。

(6)

水利工程在正常运用过程中，由于洪水作用导致防洪参数F超过设计值f设的平均间隔时间定义为水利工程的设计防洪重现期Tf设，即水利工程设计防洪能力被超过的重现期，则：

Tf设=1/P(F>f设=f(x设1,x设2,…,x设n))。

(7)

由于防洪参数F超过设计参数f设时，水利工程的正常运用将遭到破坏，因此设计防洪重现期与水利工程在洪水作用下正常运用遭到破坏的平均间隔时间相等，即Tf设=T破坏=1/P破坏。以设计防洪重现期表示防洪标准更加符合防洪标准的内涵。

在多个洪水共同作用下，同一Tf对应的洪水组合也有无数种，但每种组合的危险域都一致，且对水利工程的威胁一致，以其中任意一种组合进行调洪演算得到的水利工程参数相等，如图5、图6所示。Tf与T∨、T∧、Tk相比较，不但不会出现大重现期危险域与小重现期危险域有交叉的问题，更重要的是以设计防洪重现期作为防洪设计标准进行设计，得到的水利工程防洪能力确定，设计防洪重现期与水利工程防洪能力具有一一对应性。

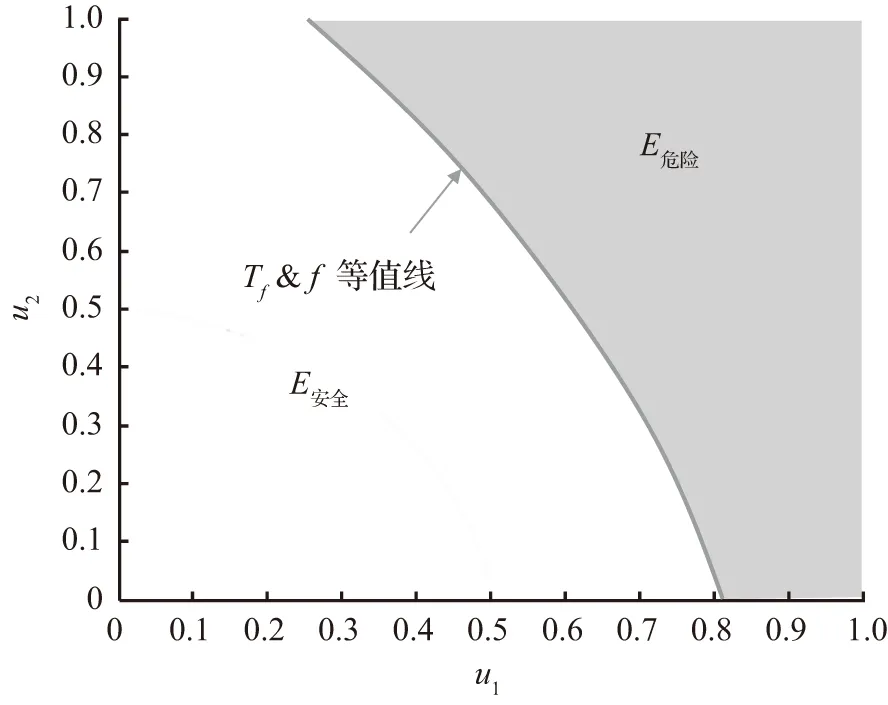
图5 防洪重现期的危险域与安全域Fig.5 Risk and safety regions for flood control reproduction period

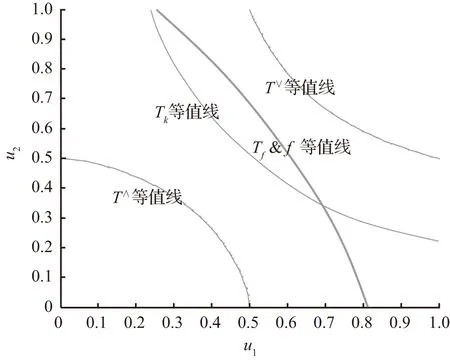
图6 防洪重现期与洪水重现期对比Fig.6 Comparison of flood control recurrence period and flood recurrence period

在多个洪水共同作用的情况下，同一洪水重现期的不同洪水组合对应的防洪参数f值不等，按给定的T设洪进行设计得到的水利工程的防洪能力不确定，水利工程正常运用遭到破坏的平均间隔时间也不确定。同一防洪重现期的不同洪水组合对应的防洪参数f值相等，以Tf设作为防洪标准进行设计得到的水利工程防洪能力确定，水利工程正常运用遭到破坏的平均间隔时间T破坏等于Tf设，但不等于设计洪水对应的洪水重现期。

2.2 基于防洪重现期的水利工程防洪设计参数

Tf设与防洪参数F的设计值f设的关系如下：

(8)

以Tf设作为防洪设计标准对水利工程进行设计确定防洪设计参数f设，可归结为根据(8)式已知Tf设求f设，由于(8)式的关系涉及调洪计算等，难以采用具体数学方程表示，本文采用蒙特卡罗模拟的方法求解[13-14]。具体求解方法主要包括以下3步：

①给定多个洪水X=(X1,X2,…,Xn)T的联合概率分布模型，采用随机抽样方法获得N场洪水组合。Copula函数已经被证明为有效的描述多变量水文事件的方法[15-17]，多个洪水的联合概率分布模型可采用Copula函数描述[18-19]。在利用Copula理论建立联合概率分布函数的基础上，随机洪水组合的生成包括以下3步：

a)抽取[0,1]的独立标准均匀分布变量V=(V1,V2,…,Vn)T；

b)将V=(V1,V2,…,Vn)T转化为服从联合分布函数的相关标准均匀分布变量U=(U1,U2,…,Un)T；

c) 将U=(U1,U2,…,Un)T映射为洪水变量X=(X1,X2,…,Xn)T。

②将洪水组合Xi代入调洪模型进行调洪计算，得到各场洪水对应的防洪参数F。

③对F进行排频统计，根据P(F>f设)=1/Tf设即可得到防洪设计参数f设，满足F(X1,X2,…,Xn)=f设的洪水组合即可作为Tf设对应的设计洪水组合。

3 应用实例

3.1 工程背景

桂平航运枢纽位于广西桂平市郁江河段，是一个集航运、发电、灌溉、交通于一体的综合利用性航运枢纽工程，处于郁江与西江干流(包括黔江、浔江)汇合口附近的郁江段，主要由航运船闸、溢洪坝及水闸组成[20]，见图8。非洪水时期，溢流坝水闸关闭，枢纽坝上水位抬高以保证航运水位以及发电；洪水时期，溢洪坝水闸打开，洪水通过溢洪坝水闸下泄。桂平航运枢纽同时受到郁江和西江干流洪水的作用，汇合口的郁江上游附近有贵港水文站、干流下游附近有大湟江口站水文站[21-22]。下文在利用Copula函数建立干流和支流洪水联合分布的基础上，利用设计防洪重现期确定桂平航运枢纽溢洪坝水闸的防洪设计水位并进行对比分析。

图7 桂平航运枢纽位置及组成Fig.7 Location and composition of Guiping Shipping Hub

3.2 联合分布模型

西江干流选择大湟江口站1951～2010年实测洪水系列，郁江以大湟江口站发生最大洪峰流量的时间为控制，统计贵港站相应场次洪水的相应洪峰流量并进行频率计算及P-III型曲线适线得到边缘分布u1=F1(x1)，u2=F2(x2)。

采用干流Clayton Copula函数建立联合分布模型，Clayton Copula表达式如下：

C(u1,u2)=(u1-θ+u2-θ-1)-1/θ;θ∈(0,∞)，

(9)

式中：u1和u2为西江干流洪峰变量X1和郁江洪峰变量X2的边缘分布函数，θ为Copula函数的参数，可根据干、支流洪峰系列的肯德尔相关系数τ采用下式计算：

τ=θ/(2+θ)，

(10)

经计算得到的边缘分布参数见表1，Clayton Copula函数的参数值为0.35，具体计算过程详见文献[23]。

表1 边缘分布函数的统计参数值Tab.1 Statistical parameter values of edge distribution functions

3.3 防洪重现期与防洪设计水位

①同一Tf的所有洪水组合对应的洪水位Z一致，且Tf越大，对应的Z越大，其中Tf设=100 a对应的防洪设计水位Z设统一为43.54 m。

②根据设计洪水重现期计算Z设，设计洪水组合可以分别位于T∨、T∧、Tk等值线上，各可能的设计洪水组合计算得到的Z设差异巨大，可从35.57～45.37 m不等。由于Z设与设计洪水重现期无一一对应关系，以设计洪水重现期确定的Z设具有随意性，且Z设的大小差别可达10 m甚至更大，已经完全脱离合理的误差范围，可以认为以设计洪水重现期确定Z设会导致完全错误的结果。

图8 为不同Tf及对应洪水位图Fig.8 For different Tf and corresponding flood levels

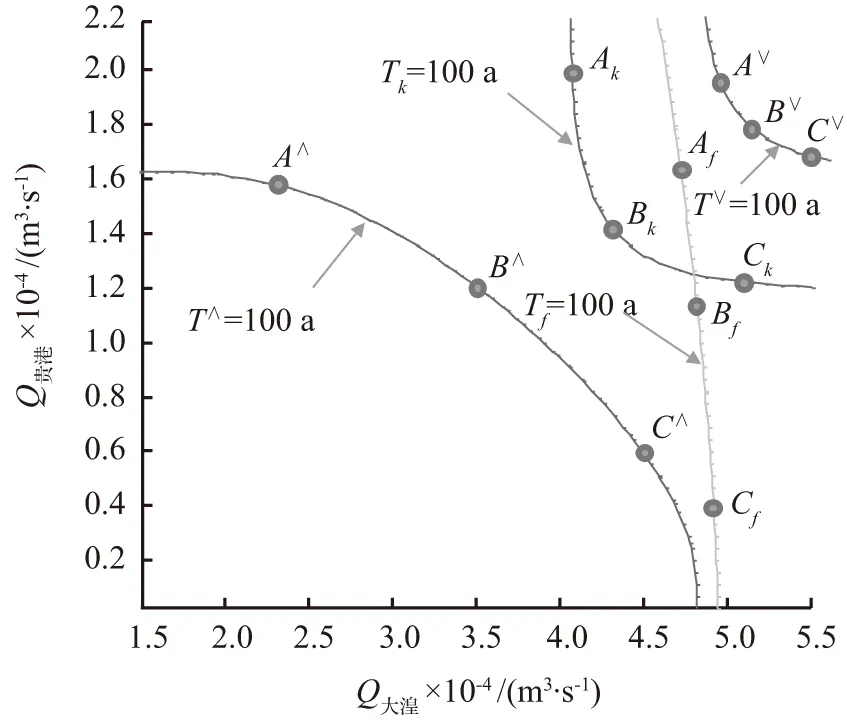
9 不同计算重现期对应的设计洪水组合对比Fig.9 Comparison of design flood combinations for different calculated reproduction periods

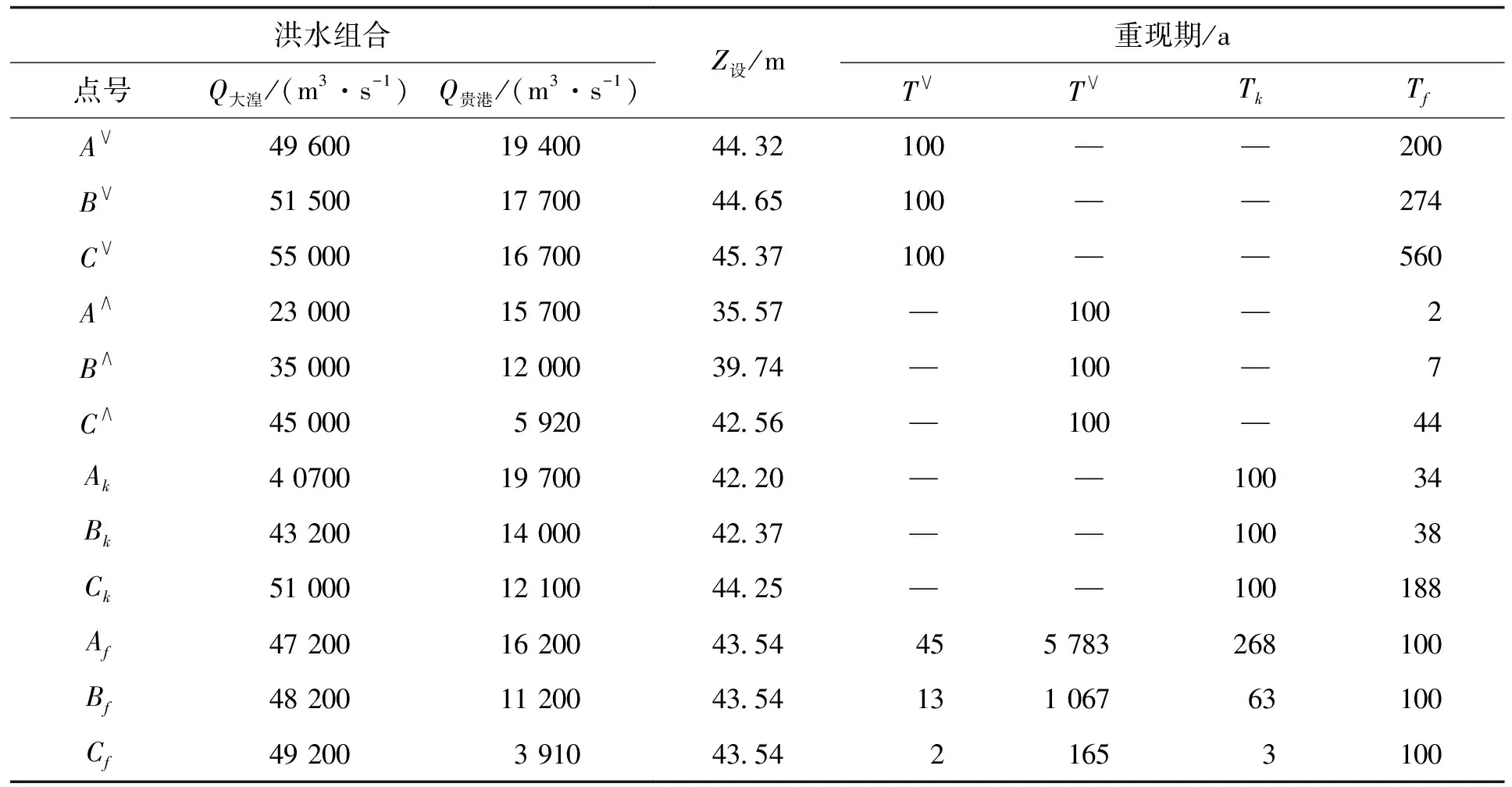
表2 计算设计洪水位与设计洪水对比Tab.2 Comparing design flood level with design flood level

③以Tf=100 a确定防洪设计水位为43.54 m，对于所有可能发生的洪水，洪水位超过43.54 m的平均间隔时间为100 a，水利工程的防洪能力可达到防洪标准的要求。

④以设计洪水重现期确定Z设，对于可能发生的洪水，洪水位超过Z设的平均间隔时间不确定且不等于100 a，其中根据T∨计算的平均间隔时间超过100 a，根据T∧计算的平均间隔时间小于100 a，根据Tk计算的平均间隔时间可能超过100 a，也可能小于100 a。

3.4 设计防洪重现期与设计洪水重现期危险域

以Tf设=100 a进行设计的危险域与安全域如图10(a)所示。以Tf设=100 a进行设计认定的危险域Ef危险中的所有洪水组合的Tf>100 a，且对应的洪水位Z全部大于设计洪水位Z设；认定的安全域Ef安全中的所有洪水组合的Tf<100 a，且对应的洪水位Z全部小于设计洪水位Z设。可见，以Tf设=100 a进行设计认定的危险域和安全域完全符合防洪标准对于防洪能力的要求。

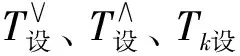
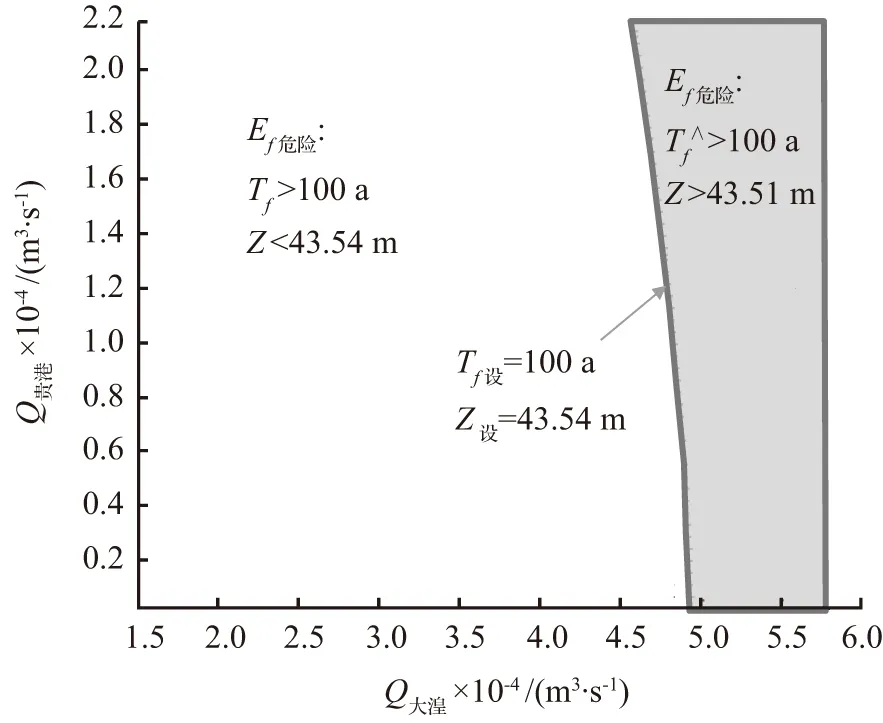
(a) Tf设及其危险域、安全域

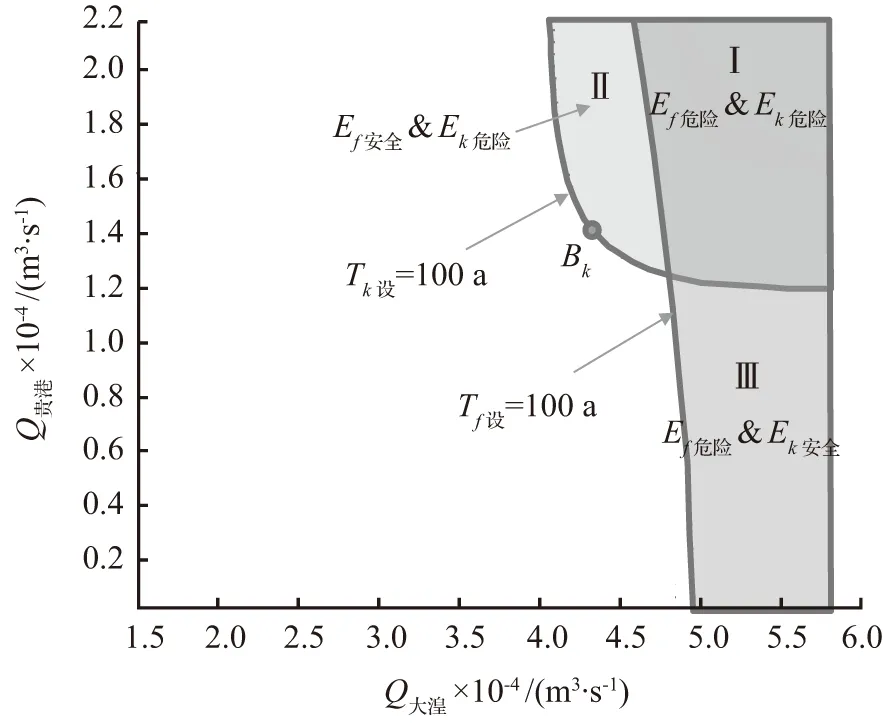
(d) Tf设与Tk设的危险域对比

4 结论

本文针对多个洪水共同作用下的水利工程设计过程中采用设计洪水重现期表示防洪标准、以设计洪水重现期计算设计洪水及防洪设计参数存在的问题展开了深入的探讨。结论如下：

①多个洪水作用下同一洪水重现期对应的洪水组合有无数个，且各洪水组合对水利工程的威胁差异非常大，以设计洪水重现期计算防洪设计参数可能会得到完全错误的结果，多个洪水共同作用下的水利工程防洪标准不宜用设计洪水重现期表示。

②多个洪水作用下的防洪标准表示形式必须考虑洪水与行洪边界的耦合关系，建议用防洪重现期或者结构荷载重现期表示。设计洪水重现期认定的危险域仅是根据洪水发生的概率确定，而不是根据洪水的威胁是否大于设计防洪能力认定，在多个洪水共同作用的情况下，洪水组合发生的概率与威胁并不一一对应，因而认定的危险域不一定危险，认定的安全域不一定安全，而根据设计防洪重现期确定的危险域与洪水威胁大于设计防洪能力的区域一致。

③对于多个洪水共同作用的情况，同一防洪重现期对应的洪水组合对水利工程的威胁一致，根据设计防洪重现期确定防洪设计参数可保证水利工程防洪能力确定且达到防洪标准的要求。