轴向和扭转循环加载下HRB335钢的力学行为研究

石车嗣,黄家欢,张克实*

(1.广西大学土木建筑工程学院，广西南宁530004；2.工程防灾与结构安全教育部重点实验室，广西南宁530004)

0 引言

HRB335钢材屈服强度高、变形能力强，被广泛应用于工程结构。在实际工程中，构件往往是在多轴载荷下服役的[1-3]。从破坏类型来看，金属材料的破坏通常根据断口特征被分为拉断和剪断两种类型。同一材料其抗拉破坏和抗剪破坏的能力通常会有所差别，在拉压加载和扭转加载下其本构行为也会有差别。特别是多轴载荷作用下，材料的变形行为和抗破坏能力可能会差异很大[4-6]。需要有能反映这些差异的分析模型来评估材料在相应加载条件下的力学行为[7]，为此要开展大量有针对性的试验研究，检验模型对不同加载方式下材料变形和破坏行为描述的合理性。考虑到构件在服役中往往要承受往复载荷[8-9]，因此用于相应过程分析的本构模型应能合理描述材料在复杂往复载荷作用下的力学行为。FREDERICK等[10]最早提出了非线性随动硬化模型来描述这种行为。后来CHABOCHE等[11]在此基础上作了改进，增加了各向同性硬化的描述，提出了Chaboche模型，该模型目前得到了广泛应用[12-16]。Chaboche模型待定参数较多，人们一直希望找到合理并且简便的方法，结合试验来确定这些参数。同时对于模型对复杂往复加载下材料的力学行为能否很好描述，也还需要开展进一步的检验和探讨。

为探讨不同载荷作用下材料的力学行为差异，本文对HRB335钢进行单轴拉伸、纯扭以及不同应变幅值的拉压疲劳和扭转疲劳等试验研究工作，在此基础上对相应的本构模型和疲劳寿命模型的合理性和有效性进行检验。拟通过这些研究，探讨材料在相应加载过程中的力学行为和与之相适应的模型分析方法。

1 材料、试样与试验

采用柳钢生产的热轧二级螺纹钢(HRB335，产品标准GB/T 3274—2007)为试验材料，分别进行了单轴拉伸、纯扭、低周拉压疲劳和扭转疲劳试验。HRB335钢的主要化学成分见表1，材料的基本力学性能参数见表2。表2中E为弹性模量；G为剪切模量；σs为屈服强度；σb为抗拉强度。试样形式为薄壁圆筒，其几何尺寸如图1所示。试样内外表面都进行了抛光处理(粗糙度为0.4)，两端内孔用过盈配合的金属堵头堵上以保证可靠夹持。所有试验用MTS809拉扭电液伺服疲劳试验机在室温下进行。

表1 HRB335钢的化学成分Tab.1 Chemical composition of HRB335

表2 HRB335钢的力学性能Tab.2 Mechanical properties of HRB335 steel

单轴拉伸和纯扭试验用于考察材料的应变硬化性能和各向同性性质，而往复拉压和往复扭转试验用于检验材料在这两种路径下的循环塑性性质以及抗疲劳破坏性能的差异。其中单调加载试验是在准静态条件下进行，而往复加载试验的频率是1赫兹。

图1 试样几何尺寸Fig.1 Geometry size of specimen

2 试验结果分析

2.1 HRB335钢在单轴拉伸和纯扭单调加载下的力学行为

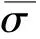
(1)

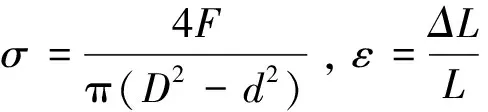
(2)

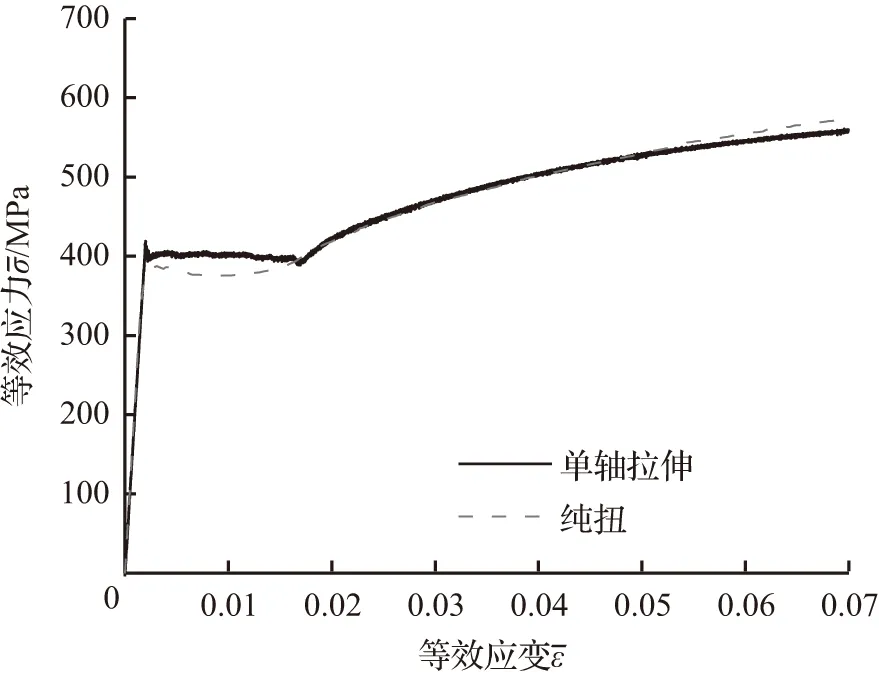
图2 HRB335钢单轴拉伸和纯扭等效应力—应变曲线Fig.2 Equivalent stress-strain curves of HRB335 steel under monotonic loading

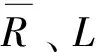
分别进行单轴拉伸试验和纯扭试验，利用等效应力—塑性应变曲线来比较单调加载、不同变形方式下材料的力学行为。图2显示的是由试验得到的HRB335钢等效应力—塑性应变曲线，知单轴拉伸和纯扭试验测得的结果是很接近的。需要指出，薄壁管试样扭转过程中应变大于0.07后屈曲导致应变测试失效，图中曲线对应的最大应变是0.07(即7 %)。经典塑性理论认为，对各向同性材料，可用J2函数描述屈服(包括后继屈服)条件，而且分别用单轴拉伸和纯扭试验得到的等效应力—塑性应变曲线重合。图2的曲线结果说明，HRB335钢的塑性行为基本与经典塑性理论描述相符，这一点与文献[17]关于纯铜的试验结果相似。

2.2 HRB335钢轴向拉压和扭转循环加载下的滞回曲线

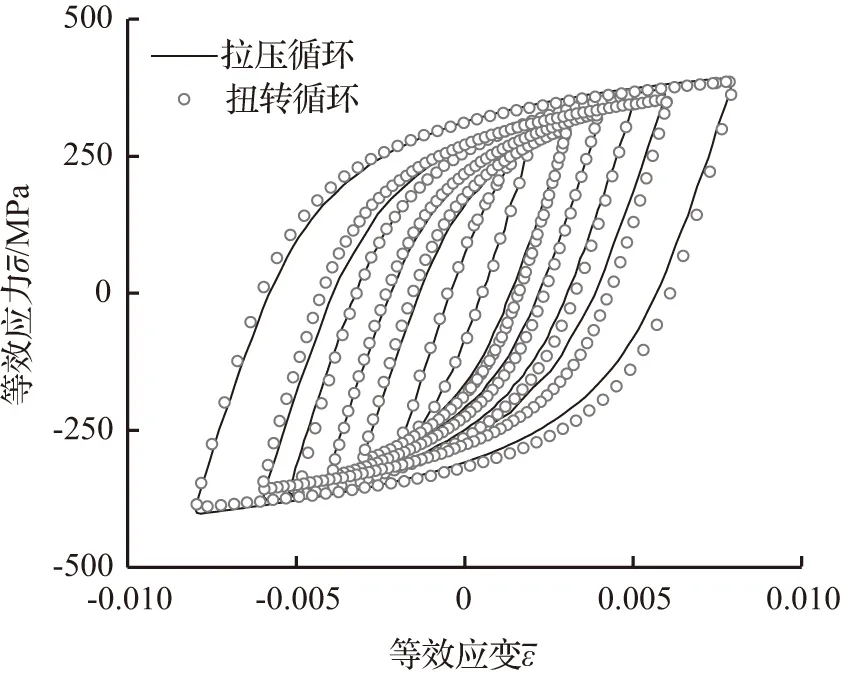
图3 两种路径下的循环应力—应变滞回曲线Fig.3 Cyclic stress-strain hysteresis curve under two paths

图3为HRB335钢在不同应变幅值下拉压稳定循环和扭转稳定循环的滞回曲线(等效)。由图3可知，在相同等效应变幅下，两者的稳定滞回曲线差异不大。

2.3 由轴向拉压和扭转循环试验数据标定Chaboche本构模型参数

Chaboche模型能较好地描述材料的循环塑性特性，参照文献[11,18,19]，Chaboche塑性本构模型包含以下三个构成部分。

①Von Mises型屈服条件:

(3)

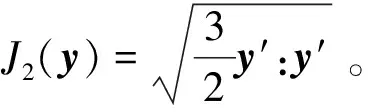
(4)

式中：Q是R的饱和值，b是材料常数。Δεp是增量塑性应变张量，p是等效塑性应变的累积值。

②正交流动法则:

(5)

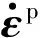
③非线性运动硬化律。

非线性运动硬化通过背应力α的演化反映屈服面中心的移动。为了能逼近循环试验得到的应力应变曲线，背应力及其率表示为多个分量的叠加:

(6)

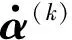
标定Chaboche模型参数要结合数值模拟来进行。为方便处理，笔者针对轴向和扭转变形将上述张量本构模型退化为一维模型，可不通过有限元计算来模拟轴向和扭转试验过程。

2.3.1 针对轴向和扭转变形试验分析的Chaboche模型积分算法

单轴拉压下，对于塑性体积不可压缩的材料，由公式(3)可分别得到拉压和扭转作用下的屈服准则：

(7)

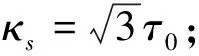
于是由正交流动法则式(5)，对应拉压和扭转试验的等效塑性应变增量可分别按一维表达形式写出：

(8)

其中:Δγp是塑性工程切应变的增量。

将弹性正应变、切应变和塑性正应变、切应变分别记为εe、γe和εp、γp。在小应变情形下总应变和增量应变可分解为弹性应变和塑性应变之和，即有：

ε=εe+εp,Δε=Δεe+Δεp,γ=γe+γp,Δγ=Δγe+Δγp。

(9)

于是，第n+1步下有：

(10)

由胡克定律有：

(11)

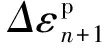
(12)

用以下屈服准则判别材料是否屈服：

(13)

如检查结果是弹性，转为下一增量计算；若试探应力超出了屈服半径，则需要计算塑性应变增量。只要得到准确的塑性应变增量，就可由式(9～11)计算得到所需的应变和应力。以下给出在上述公式基础上构造的求解塑性应变增量的一维非线性方程。

对由方向性硬化导致的背应力的变化率，可将公式(6)对应拉压和扭转情形退化可得到下式

(14)

将式(14)前两式分别积分，可得：

(15)

且

(16)

由式(11)和式(12)，有

(17)

由式(15)～(17)并注意到式(8)，可以得到：

(18)

式中正负号分别对应于拉伸和压缩情形，而扭转以正向加载为正，反向加载为负。在材料满足屈服条件式(7)时，由式(18)可得到:

(19)

式中，Rn+1由下式计算:

Rn+1=Q{1-exp[-b(pn+Δpn+1)]。

(20)

可知式(19)是只含单未知量Δpn+1的一维非线性方程，它可用标准的Newton-Raphson迭代方法来求解。

以上分析表明，对于循环单轴拉压和扭转试验，可采用一维非线性迭代方法对循环滞回曲线进行Chaboche模型分析。笔者按上述方法编写了相应的计算程序，并在下面将其用于HRB335钢材在循环单轴拉压和扭转试验下的Chaboche模型参数确定，和该材料在循环单轴拉压和扭转试验下的本构行为分析。

2.3.2 Chaboche模型材料参数的确定与检验

针对“2.2 试验结果分析”介绍的实测循环稳定应力应变滞回曲线，用上节建议的针对循环试验的Chaboche本构模型计算方法，参照实测拉压循环稳定滞回曲线(因为拉压循环和扭转循环的滞回曲线差异很小)标定了HRB335钢材的Chaboche模型参数，结果见表3。

表3 HRB335钢材的Chaboche模型材料参数Tab.3 Material parameters of Chaboche model for HRB335

为证实本文方法的有效性，下面先以控制应变幅为0.005的试验为例来进行检验。图4展示了实测循环单轴拉压[图4(a)]和扭转[图4(b)]试验的稳定滞回曲线，而相应的用“2.3.1 针对轴向和扭转变形试验分析的Chaboche模型积分算法”介绍的计算方法与表3给出的Chaboche模型参数结合计算的曲线也绘在了图中。由图4可看到，计算曲线与实测曲线吻合很好，说明本文建议的针对循环单轴拉压和扭转试验分析的Chaboche模型计算方法是有效的。

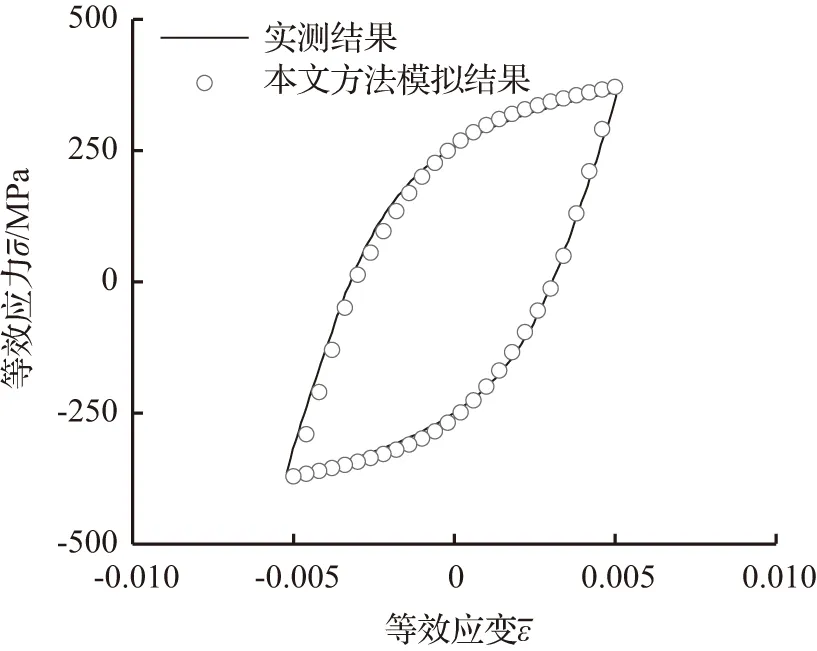
(a) 单轴拉压循环

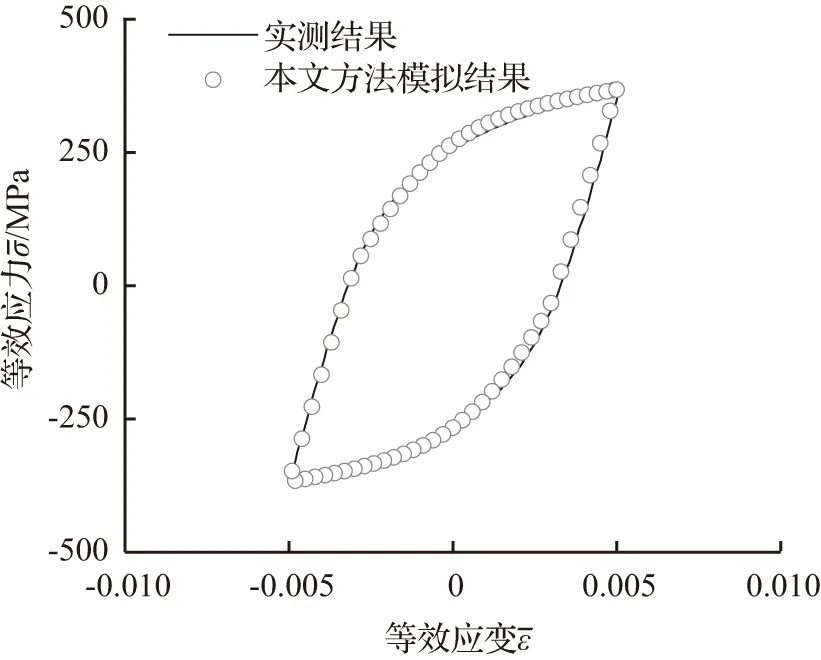
(b) 扭转循环

用表3列出的模型参数，通过本文方法与ABAQUS软件方法作比较来进一步检验。两种方法的计算结果曲线见图5，同时将它们与实测滞回曲线进行比较。图5表明，两种计算的结果几乎完全吻合，验证了本文方法和程序的正确性，同时验证了Chaboche模型能准确、合理地描述金属材料的稳态循环特性。由于本文方法计算规模小，可方便地在试验数据处理计算机上运行，可以快速简便的通过试算标定Chaboche模型的参数。

(a) 单轴拉压循环

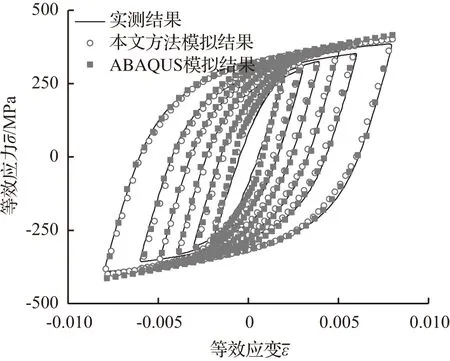
(b) 扭转循环

3 HRB335钢在轴向拉压和扭转循环加载下疲劳寿命差异

拉压加载和扭转加载下试样材料的应力和应变状态是不同的：①拉压加载是单向应力状态，扭转加载是双向应力状态；②拉压加载时三轴应力度的数值在正负1/3两端跳动，而扭转加载下三轴应力度的数值始终为零；③拉压加载时Lode参数的数值在正负1两端跳动，而扭转加载下Lode参数的数值始终为零。

将HRB335钢拉压加载和扭转加载下测得的疲劳寿命试验结果一并绘于图6。从图6展示的数据对比可以看出，在相同等效应变幅下，HRB335钢材扭转循环作用下的疲劳寿命值与拉压循环作用下的寿命值有差异，扭转循环下材料的疲劳寿命较短。但随着应变幅降低，寿命差异也降低。

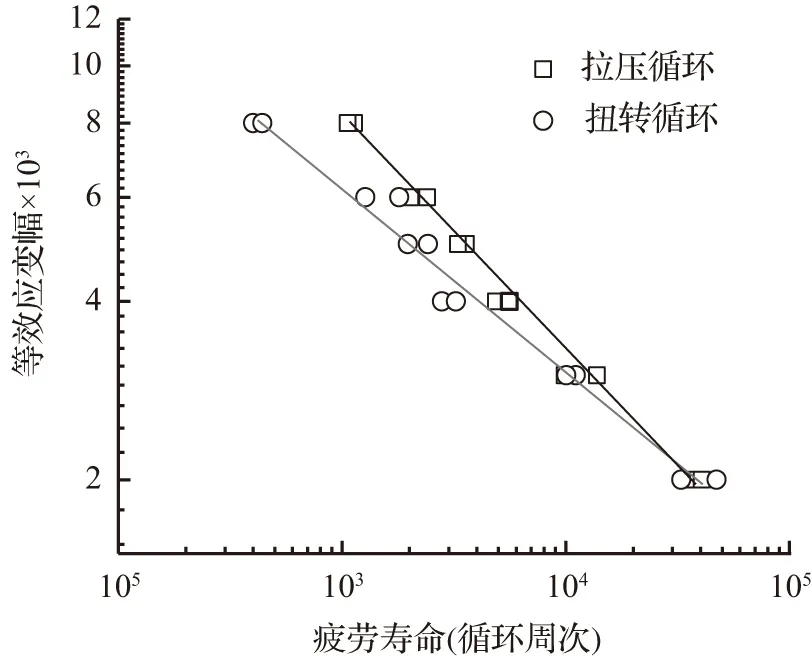
图6 两种路径下等效应变幅与疲劳寿命的关系Fig.6 Relationship between equivalent strain amplitude and fatigue life in two paths

4 结论

①单调加载时，HRB335钢的拉伸和扭转等效应力等效应变曲线差异很小，当等效应变幅相同时，HRB335钢的拉压循环和扭转循环稳定等效滞回曲线的差异也很小;

②HRB335钢材扭转循环疲劳寿命值与拉压循环寿命值有差异，但随着应变幅降低，寿命的差异也降低;

③本文建议的针对循环单轴拉压和扭转试验的Chaboche本构模型计算方法与有限元软件ABAQUS的方法计算的滞回曲线结果吻合，但本文方法应用更简便。