复杂条件下深基坑围护结构变形演化规律研究

麻凤海,陈霞,刘增斌

(大连大学建筑工程学院，辽宁大连116622)

0 引言

深基坑工程围护结构的稳定对于施工安全与基坑的整体稳定具有重要意义，其中降水过程会影响基坑内外渗流场的变化，因此要选取适当的降水方案，孔隙水压、总水头的变化能较好地反映降水进程，降水方案的优化可以减少基坑周围地表沉降，保持基坑整体处于相对稳定的弹性状态；在开挖基坑的过程中，基坑除了自身的长跨效应外，还具有时空效应，土体开挖卸荷作用改变了原有的应力状态，使得内侧土体对围护结构的支撑作用减小，此时围护结构的稳定对基坑的稳定有重要作用，土方开挖的方式也会影响基坑的稳定，一般超挖到钢支撑架设处以下0.5 m，如果超挖深度较大，将引起基坑发生较大变形，不利于基坑的稳定；另外，围护结构的施工也会影响土体的应力重分布，适当的注浆方式能够有效减少对土体的扰动，有利于基坑的稳定；基坑两侧堆载的形式也影响了基坑的稳定，对称荷载或不对称荷载都会影响围护结构的沉降和变形，进而影响基坑的稳定性。因此，研究复杂条件下的深基坑围护结构的稳定性具有十分重要的现实意义。

李兵等[1]运用理正深基坑结构设计软件研究了桩径、桩间距的不同对围护结构内力、变形的影响，结果表明：在基坑稳定的前提下，增大桩间距能增大围护桩的位移变形，减少围护桩总数，节约了施工成本；李方明等[2]基于江漫滩地铁深基坑的变形实测资料，采用了理论公式分析结合有限元数值模拟的方法，总结了悬挂式帷幕基坑的变形规律，结果表明：其地表沉降曲线呈凹槽形，地下连续墙的最终形态为内凸胀肚型；夏元友等[3]对武汉市某一超大型深基坑地连墙跳跃式施工过程进行了三维有限差分数值模拟，研究了对单个跳跃式开挖过程墙上土压力的监测，揭示了地下连续墙施工影响应力重分布的变化规律；XIAO等[4]运用有限元数值模拟的方法得出了深基坑开挖深度方向水平位移的变化规律和围护桩的水平位移变化规律，得出围护桩顶部的水平位移是基坑开挖深度的0.2 %～0.5 %，地表最大沉降发生在距离基坑顶部0.6倍开挖深度处附近；QING等[5]运用一阶可靠性方法、响应面法即RSM法来进行岩石隧道稳定的可靠性分析，研究表明喷射混凝土厚度及其安装的位置可以优化圆形岩石隧道的设计；DEBASIS等[6]分析了几种加固围岩的数值分析方法，结果表明：单个的节点、螺栓及它们之间的相互作用可以用来分析在加载条件下岩体开挖的稳定性，得到的岩体应力和位移的结果可以和未用螺栓加固的岩体模型进行对比；席培胜等[7]利用MIDAS GTS NX对基坑典型控制截面建立二维模型，分析2种堆载：对称和非对称的情况下支护桩水平位移的变化规律，结果表明：堆载的形式对桩体水平位移有明显影响，非对称荷载作用下的桩体位移具有明显的非对称性；李涛等[8]以北京地铁10号线一盾构井深基坑工程为例，采用FLAC3D软件进行数值模拟，分析了支撑轴力和桩体水平位移的相互作用机理，研究表明：钢支撑轴力在安装完成后不久达到最大值，然后逐渐减小趋于稳定，其中最大值发生在角撑处；钢支撑对桩体水平位移有一定限制作用，桩体最大水平位移的位置随基坑开挖的深度逐渐下降；王佳庆等[9]以成都地铁2号线一深基坑为例，考虑到该基坑处于膨胀土地区，必须考虑水平膨胀力的影响，运用MIDAS/GEN软件模拟了膨胀力作用下围护桩的受力，结果表明：考虑膨胀力之后的围护结构体系造价增大，加大了安全储备又合理地控制了施工成本；代祥等[10]运用PLAXIS 2D模拟基坑开挖过程中有无架设钢支撑支护桩内力和位移变化规律，模拟结果发现：架设钢支撑能减缓基坑偏移速率，在距围护桩桩底H/3-2H/3处，偏移量最大，呈“弓”形分布；YAN等[11]运用应变软化模型来模拟岩体，用剪切和螺栓拉伸失稳来检验岩体支撑系统的稳定性，结果表明：当k0取0.5～1.25时，数值模拟结果与现场实测有较好的吻合，且岩体当中的主要断层和软弱夹层对结构的位移和应力有显著的影响；SUN等[12]建立二维和三维有限元模型，详细分析了由于作用在深基坑内外土体压力的不同，导致围护结构所受荷载和水平位移的不同；李四维等[13]分析了基坑尺寸、桩体的嵌固深度、施工工况对基坑变形规律的影响；安建永等[14]提出了地层损失随时间变化的模型，给出了地表沉降随时间、施工参数变化的函数表达式；付涛等[15]研究了悬臂式排桩围护结构的位移和弯矩的分布规律，并将解析法和模拟结果进行对比分析；张明远等[16]研究了顺作、逆作工法下，基坑围护结构和相邻隧道的位移特点以及两者之间的关系，结果表明：逆作法会明显减少围护结构的侧向位移；赵秀绍等[17]运用FLAC3D建立了深基坑开挖支护的模型，得到了不同开挖阶段的地表沉降、围护结构的位移变化规律。

这些文章极大程度地推动了对基坑围护结构的认识和发展，但对于复杂条件下深基坑围护结构稳定性的研究相对较少，大部分数值模拟对工况的模拟过于理想化，不能全面反映基坑整体变形。因此，有必要进一步进行研究。

本文以沈阳市地下综合管廊(南运河段)第20号盾构始发井深基坑工程为背景，运用MidasGTS软件建立基坑开挖三维地层模型，对开挖支护的全过程进行模拟，并将计算结果与现场监测数据进行对比，得到了始发井深基坑围护结构的变形规律，为类似工程的设计和施工提供一定的参考和借鉴。

1 工程概况

本文选取盾构始发井(D5)进行研究，该盾构井起点里程右线：K8+202.769，终点里程右线：K8+254.369,位于万泉公园湖水中,沿南运河南侧东西向布置，中心里程为K8+228.569，结构平面外轮廓尺寸为51.6 m×22.6 m，坑深约21.6 m，标准段宽度约18.8 m，深约18.6 m该盾构始发井为三层三跨箱形框架结构，采用钻孔灌注桩+坑内钢支撑的围护结构体系，基坑采用坑外降水的方式，桩间土采用挂网喷射混凝土保护。钢支撑采用直径609 mm，厚度16 mm的钢管撑，共设3道，两端盾构井增设一道换撑。为减小围护结构的变形，本工程对所架设钢支撑预加轴向力。围护桩桩径800 mm,桩间距1 200 mm。地层主要物理力学参数见表1。

表1 地层土体的物理力学指标Tab.1 Numerical simulation parameter of stratum list

2 数值模拟

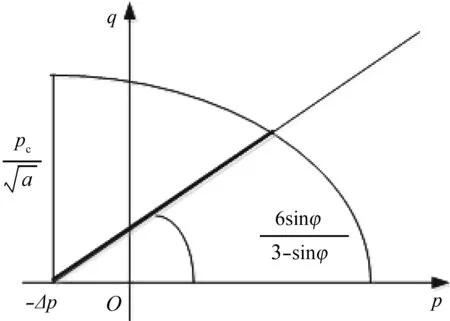
图1 修正摩尔—库伦模型在p-q平面屈服准则Fig.1 Yield criterion of modified Mohr-Coulomb Model in P-q plane

利用MidasGTS软件建立基坑三维模型，考虑到基坑周围土体开挖的影响范围，本盾构始发井基坑所建模型的长、宽、深空间尺寸为150 m×150 m×63 m。计算模型的三维单元网格如图2所示，其中单元总数为69 658，节点总数为42 388。主要影响范围内的地层土的物理力学指标见表1。其中，围护桩和钢支撑选择弹性模型，其中钢支撑的弹模取2.1×108kN/m2，直径为609 mm,厚度为16 mm，泊松比取0.2，围护桩的弹模取3.15×107kN/m2，泊松比取0.2。用梁单元模拟钢支撑、冠梁和腰梁，板单元模拟围护桩，三维实体单元模拟土体。模型的边界条件为：模型上部的边界是地表，为自由界面，侧面和底面为位移边界，底面的位移边界为固定边界，约束水平和竖直方向的移动；侧面的边界条件是约束水平方向上的移动。

本文土体采用修正摩尔—库伦(MM-C)模型进行模拟。修正摩尔—库伦本构模型，是在摩尔—库伦本构模型的基础上加以改进而得到的，他的压缩屈服面呈“帽子形”，剪切屈服面和摩尔—库伦模型的相同，偏平面采用圆角处理的方式，和摩尔—库伦模型相比，计算结果更易于收敛。图中，横坐标p表示主应力，纵坐标q表示等效剪应力,构成的应力空间为p-q应力空间，φ为内摩擦角，pc为平均主应力，α和下式中的β1、β2都是盖帽屈服面的参数，Δp表示移动剪切屈服面，可以反应粘聚力的效果。

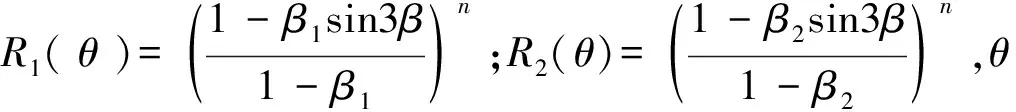
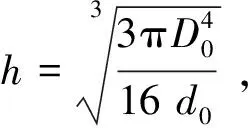
图2 三维有限元计算模型Fig.2 Three-dimensional model diagram

图3 围护桩墙和钢支撑模型图Fig.3 Model diagram of retaining pile and steel shotcrete

施工阶段分析过程如下：第1步平衡初始地应力； 第2步开挖2.8 m厚的回填土；第3步施工围护桩墙；第4步开挖第一层1.1 m厚的土体；第5步激活冠梁和第一道支撑并开挖6.4 m厚土体；第6步激活第1道腰梁和第2道支撑并开挖7.1 m厚土体；第7步激活第3道腰梁和第3道支撑并开挖3.48 m至坑底；第8步激活第4道支撑和第4道腰梁。

3 现场监测

在开挖基坑之前，布设相关监测点，在基坑开挖的过程中，进行围护桩水平侧向位移的监测，监测点的布置如图4所示。

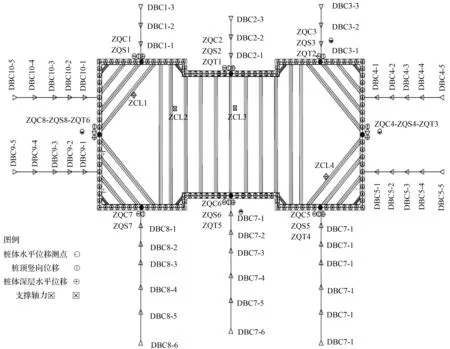
图4 监测布点平面示意图Fig.4 Planar graphs of monitoring points

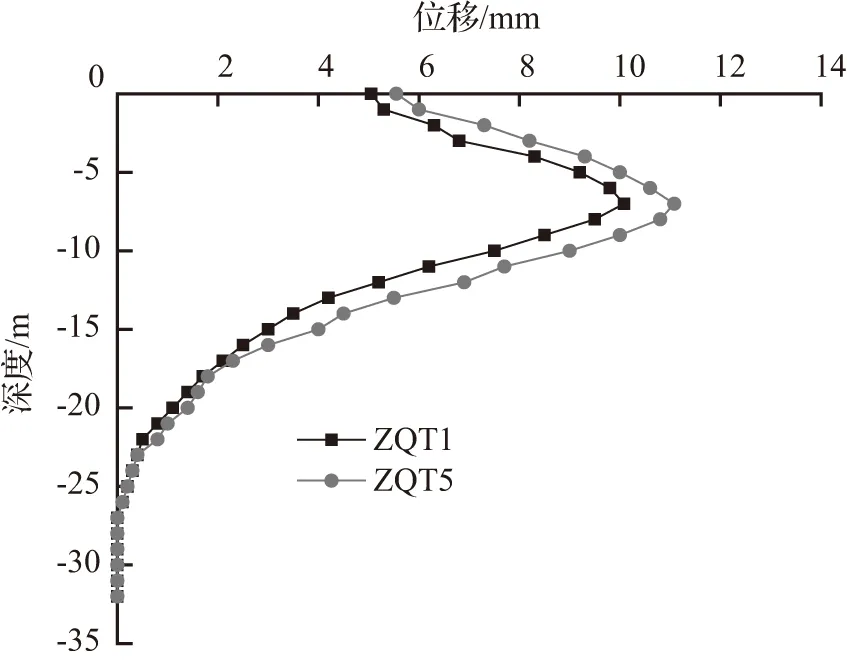
图5 开挖结束后桩身水平位移曲线Fig.5 Horizontal displacement curve of end of pile excavation

3.1 围护结构深层水平位移分析

本始发井深基坑采用钻孔灌注桩作为围护结构，对围护桩的位移进行实时监测有着重要的现实意义：确保基坑、周边建筑物、地表沉降、地下管线的稳定，要确保桩体的最大位移不能超过控制值(累计值达25 mm)，采用测斜仪对测斜管双向监控量测，对围护结构竖直方向的不同深度在不同开挖阶段内进行测量，及时记录围护结构的位移变形规律。图5为开挖结束后桩体的深层水平位移曲线。

选取ZQT1与ZQT5断面进行研究，由图5可知：

①架设钢支撑能够明显限制围护桩的水平位移，由于第一道钢支撑不能及时架设，此时的围护桩近似于悬臂梁的状态，上部发生较大的变形，位移明显前倾，但架设钢支撑之后，预加力发挥明显作用，显著限制桩体位移；

②钢支撑的架设时间、预加轴力的大小、开挖的深度等都对围护桩的位移有较大的影响。

4 数值模拟结果

在本工程中，土体、围护桩、钢支撑作为相互作用的一个整体，土方开挖基坑卸荷，改变了原来的应力平衡状态，使得应力重分布。图6～图9为各开挖步骤下围护结构的水平位移云图。

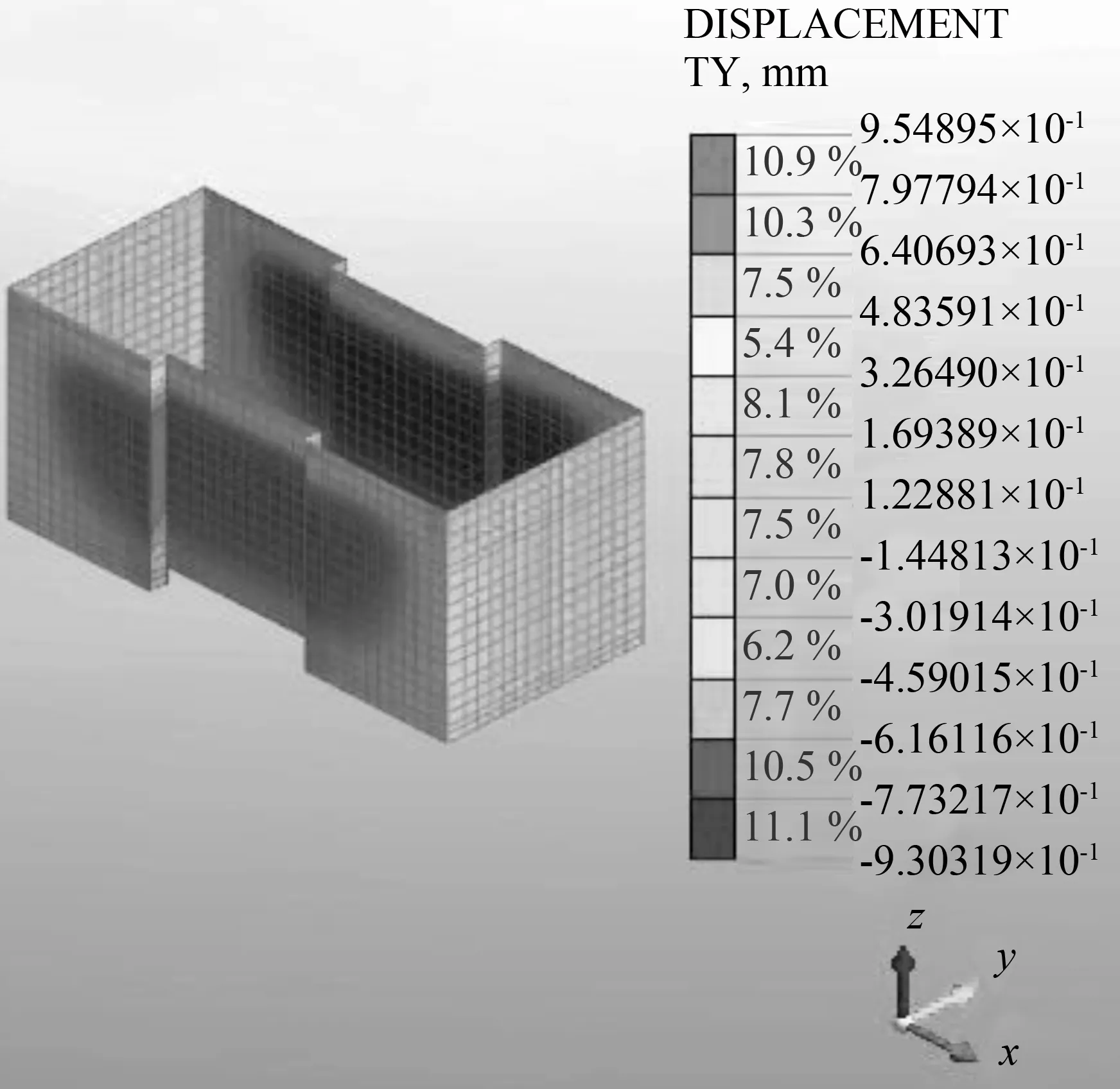
(a) 开挖1位移云图

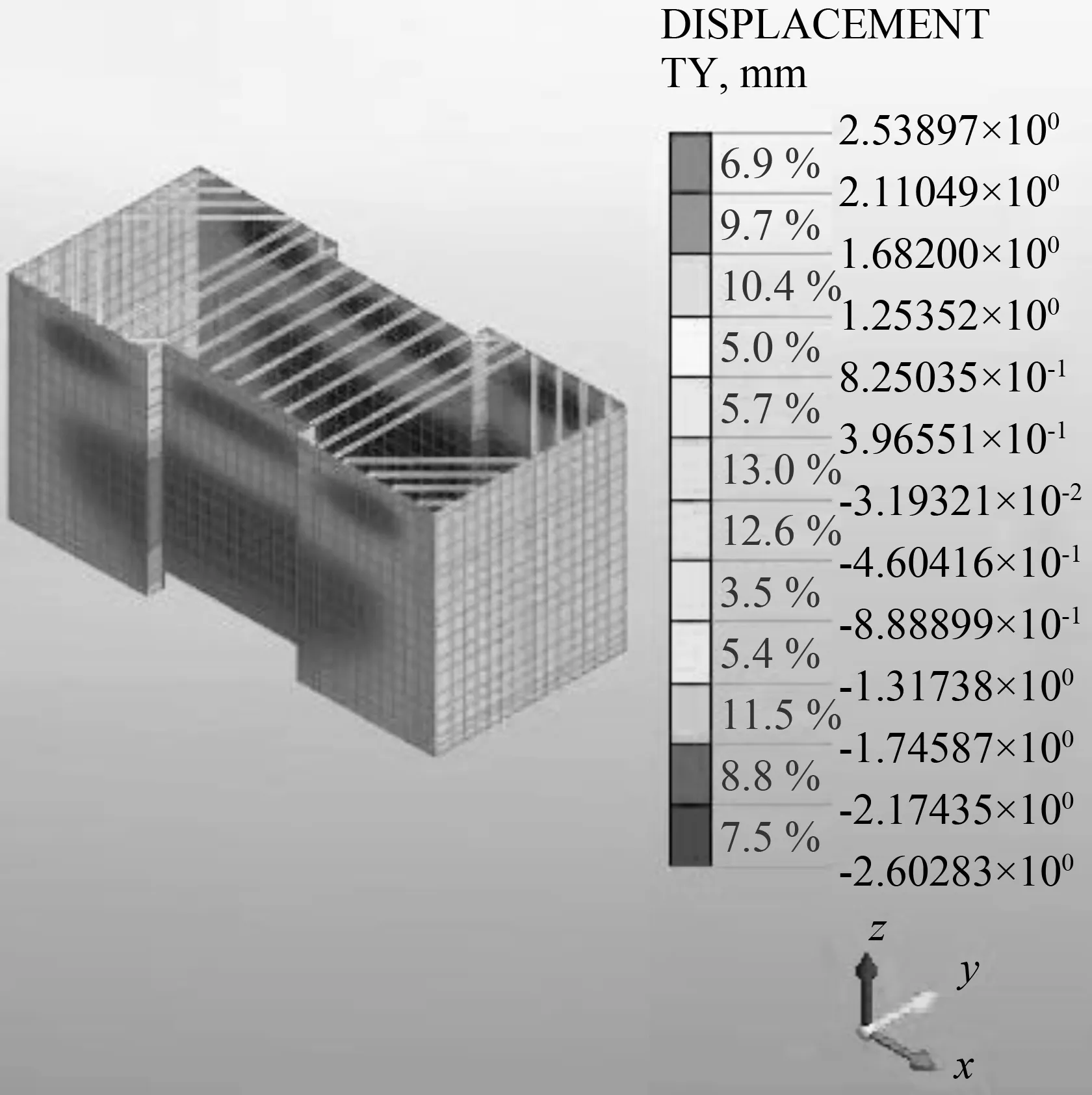
(b) 开挖2位移云图

(c) 开挖3位移云图

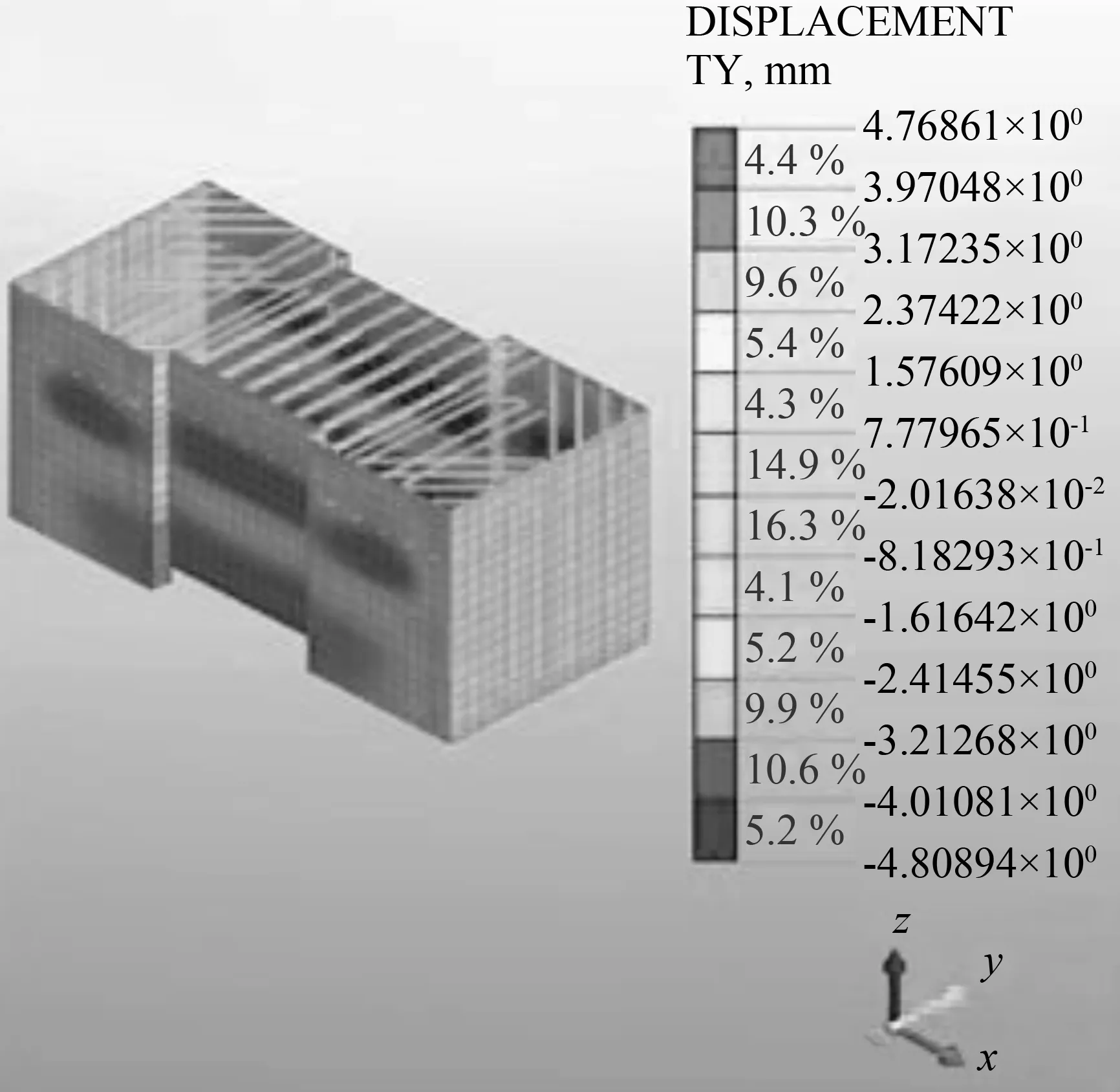
(d)开挖4位移云图

图7 基坑总体位移云图Fig.7 Total displacement of foundation pit

从数值模拟的计算结果可知：①随着基坑开挖深度的不断增加，围护结构水平位移也不断增加，两者的变化量成正比。第1步开挖后，围护桩墙的水平位移不大，受力类似于悬臂梁，其位移最大值在桩顶，此后不断减少；第2步开挖完成后，位移分布有了一些变化，位移最大值出现在开挖面8 m附近的位置；第3步开挖后，随着前2道钢支撑的架设，围护桩墙的最大位移开始向基坑的中下部移动；第四部开挖结束后，可以明显看出，基坑中部位移量最大，上部位移变化稳定。因此，需要在基坑中部位置加强架设钢支撑，且要及时架设，减少土体暴露在外的时间。②围护结构的水平侧移具有显著的角部效应，其影响范围约为基坑开挖深度的2.5～3.0倍，在基坑角部附近较小，而后呈逐渐增大的趋势。③基坑长边和短边的最大位移值均在开挖结束后，短边最大水平位移值为10.8 mm，长边最大位移值为16.7 mm，小于警戒值25 mm，所以围护结构始终处于弹性状态，基坑较为稳定。④钢支撑的架设对限制围护结构的水平位移较为显著，架设钢支撑后，围护结构的受力状态改变，类似于杆件体系，抵挡土压力的能力增强，使作用在围护桩墙上的部分土压力转向了基坑的另一侧。第1道钢支撑架设完，约束作用最为明显，但随着开挖深度的增加，钢支撑对围护结构水平位移的约束效果逐渐降低。⑤土体开挖，使围护桩内侧的压力降低，部分土体卸荷回弹，竖直方向上得到恢复，产生了水平方向上的移动，围护结构底部的位移增加。⑥基坑长边的变形明显大于短边，靠近基坑方向的位移大于远离基坑方向的位移，且基坑总体位移的影响范围约为1.5倍的基坑深度。

5 对比分析

选取ZQT1与ZQT5处的水平位移值与监测值进行分析，两个监测点的水平位移曲线图见图8、图9。

由图8、图9可知：①数值模拟结果与实际检测值的变化趋势相同，但模拟值小于监测值，这是由于在基坑开挖的过程中受到各种因素的影响(施工工艺，天气等)，使得模拟值与监测值有一定的出入，但这是正常的现象。也说明了模型参数、本构的选取较为正确，符合工程实际情况。②模拟值与监测值都表明，围护结构的最大水平位移值均在围护结构的中下部位。③当第1步开挖后，模拟值与监测值较为接近，但随着开挖的进行，两者出现一定的差别。这是因为，数值模拟过程中模拟的是理想的工况，钢支撑及时架设且超挖范围为0.5 m，但在实际基坑开挖过程中，往往超挖深度大于0.5 m，钢支撑由于种种原因也不能及时完成架设工作，从而造成结构变形增大。因此，可以利用数值模拟对基坑开挖进行超前了解(对围护结构的变形，地表沉降等)，进一步指导现场施工。

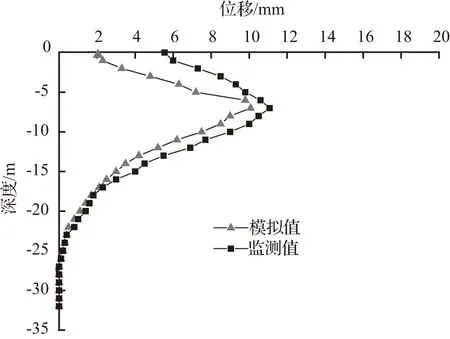
图8 开挖完成后ZQT1水平位移曲线对比图Fig.8 Horizontal displacement contrast curve of point ZQT1

图9 开挖完成后ZQT5水平位移曲线对比图Fig.9 Horizontal displacement contrast curve of point ZQT5

6 结论

本文利用MIDASGTS软件，建立沈阳市综合管廊第五盾构井(D5)深基坑开挖的三维地层模型，具体分析了在基坑开挖过程中围护结构的位移变形规律，得到了以下结论：

①围护结构的水平侧移具有显著的角部效应，其影响范围约为基坑开挖深度的2.5～3.0倍，在基坑角部附近较小，而后呈逐渐增大的趋势。

②钢支撑的架设能够显著约束围护结构的水平侧向位移，但随着开挖深度的不断增加，其约束作用不断减小，因此，需要在开挖过程中设置其他结构，保持基坑的整体稳定，可在基坑中间设置腰梁、横撑等。

③基坑长边和短边的最大位移值均在开挖结束后，短边最大水平位移值为10.8 mm，长边最大位移值为16.7 mm，小于警戒值25 mm，所以围护结构始终处于弹性状态，基坑较为稳定。基坑长边的变形明显大于短边，靠近基坑方向的位移大于远离基坑方向的位移，且基坑总体位移的影响范围约为1.5倍的基坑深度。

④随着基坑开挖深度的不断增加，围护结构的最大水平位移位置也不断向下移动，在基坑中部位移量最大，而此时基坑上部位移较为稳定。因此需要在基坑的中部位置及时加强支撑，同时减少土体暴露的时间。

⑤始发井深基坑的围护结构水平位移曲线表现为中间凸起的“大肚”形，但是当第一道钢支撑尚未架设时，围护结构的上部位移较大，表现为“前倾”形，围护结构水平位移最大值出现在基坑的中下部，在基坑底部，部分土体卸荷回弹，导致围护结构的水平位移出现增加的情况。