直觉对偶犹豫模糊集在多属性群决策中的应用

苏梦珂，孔祥智

江南大学 理学院，江苏 无锡 214122

1 引言

1965 年，Zadeh 提出模糊集[1]这一理论用于处理具有模糊性和不确定性的问题，此后，各界学者开始对其进行研究：Atanassov 通过同时考虑隶属度、非隶属度、犹豫度提出直觉模糊集[2]这一概念；Torra考虑到决策者在决策过程中可能会对隶属度值存在犹豫这一现象，提出了犹豫模糊集[3]这一概念；Zhu 等人通过定义可能隶属度与可能非隶属度提出对偶犹豫模糊集[4]这一概念。近几年来，模糊集理论发展十分迅速，已经取得了许多重要的成果。

对偶犹豫模糊集是犹豫模糊集的一个扩展，有关犹豫模糊集的研究已经十分广泛[5-12]。文献[13-14]研究了对偶犹豫模糊集的聚合算子及其基本运算；Bahram[15]研究了对偶犹豫模糊集的相关系数，在其基础上提出了区间值对偶犹豫模糊集这一新的概念，并研究了其相关系数；Zhao等人[16]首先研究了对偶犹豫模糊集的的熵应满足的公理化要求，然后构造了对偶犹豫模糊集熵的公式，最后建立了熵模型；Li 等人[17]扩大了对偶犹豫模糊集相关系数的取值范围，首次给出相关系数上下界的公式，将改进后的相关系数应用于医疗诊断与投资决策等实际问题中; Wu 等人[18]研究了对偶犹豫模糊集的相关系数，并讨论了其基本性质；Li等人[19-20]研究了对偶犹豫模糊集距离测度、相关系数等概念，并给出了基于对偶犹豫模糊集的多属性决策方法；随后，同一作者，还研究了区间值对偶犹豫模糊集的熵和相似性测度；Song 等人[21]基于对偶犹豫模糊集的概念及运算性质，引入了对偶犹豫模糊集截集的定义并给出了具体的性质。

Wu 等人[22]在直觉模糊集[23-26]与对偶犹豫模糊集的基础上，利用实数对构成的集合来表示隶属度与非隶属度，提出直觉对偶犹豫模糊集这一概念，研究了直觉对偶犹豫模糊集的集结算子的性质，并给出了具体的例子进行说明。由于直觉对偶犹豫模糊集既同时考虑隶属度、非隶属度，包含了犹豫模糊集隶属度的不确定性，又对其非隶属度进行补充，因此，可以更加细腻地描述事物的复杂性、模糊性的本质，在处理不确定性信息时具有更强的表现能力，所以，直觉对偶犹豫模糊集在处理决策问题等方面具有举足轻重的作用，值得各位学者不断研究与学习。

2 预备知识

定义1[2]设X是一个固定的集合，X上的直觉模糊集A定义为：A={＜x,μA(x),νA(x)＞|x∈X}，其中，μA(x):X→[0,1]是A的隶属度函数，νA(x):X→ [0,1]是A的非隶属度函数，且 ∀x∈X,0 ≤μA(x)+νA(x)≤1。对于X上的直觉模糊集，称πA(x)=1-μA(x)-νA(x)为x对A的犹豫程度。显然，对于 ∀x∈X,0 ≤πA(x)≤1。

定义2[4]设X是一个固定的集合，X上的对偶犹豫模糊集A定义为：A={＜x,f(x),g(x)＞|x∈X}，其中，f(x)⊂[0,1]是x∈A的可能隶属度值的集合，g(x)⊂[0,1]是x∈A的可能非隶属度值的集合。

为了方便，称H(x)=(f(x),g(x) )是对偶犹豫模糊元，简记为H=(f,g)。

定义3[22]设X是一个固定的集合，X上的直觉对偶犹豫模糊集A定义为：A={＜x,hA(x)＞|x∈X}，其中hA(x)是由若干个不同的实数对(fA(x),gA(x) )组成的集合，fA(x):X→[0,1]是A的隶属度函数，gA(x):X→[0,1]是A的非隶属度函数，且 ∀x∈X,0 ≤fA(x)+gA(x)≤1。

为了方便，称h=hA(x)是直觉对偶犹豫模糊元，并且按照降序排列直觉对偶犹豫模糊数，令σ:(1,2,…,n)→(1,2,…,n)是一个置换，满足hAσ(s)≥hAσ(s+1)，s=1,2,…,n-1。

定义4[27]设A={a1,a2,…,an} 和B={b1,b2,…,bn} 是两个参数的集合，as和bs分别是A和B中第s大的元素，则A和B之间的距离分别为：

3 直觉对偶犹豫模糊集的距离测度

距离测度是模糊集理论研究中的重要内容，已经广泛地应用于决策分析、医疗诊断等领域。在决策分析中，利用距离测度的主要优点是可以获得两种解决方案之间的差距，即每种解决方案与理想解决方案之间的差距。解决方案与理想解决方案之间的距离计算越小，解决方案越好。

比较常见的距离测度方法是Hamming距离、Euclidean 距离、Hausdorff 距离，下面基于这几种距离测度方法定义直觉对偶犹豫模糊集的一系列距离测度。

定义5设直觉对偶犹豫模糊集A、B、C是定义在论域X={x1,x2,…,xn} 上的集合，如果满足下列条件：

（1）0 ≤d(A,B)≤ 1 ；

（2）d(A,B)=0 当且仅当A=B；

（3）d(A,B)=d(B,A)；

（4）d(A,C)+d(C,B)≥d(A,B)。

则称d(A,B)是A与B间的距离测度。

下面，基于定义5研究直觉对偶犹豫模糊集的距离测度。假设直觉对偶犹豫模糊集A、B是定义在论域X={x1,x2,…,xn} 上的集合，hA(xi)和hB(xi)分别是A、B的两个直觉对偶犹豫模糊元，则两直觉对偶犹豫模糊元之间的距离测度可表示为：

其中，hAσ(s)(xi)和hBσ(s)(xi)分别为hA(xi)={(fA(xi),gA(xi))},hB(xi)={(fB(xi),gB(xi) )}中第s大的元素，l(h)是直觉对偶犹豫模糊元hA(xi)和hB(xi)中实数对的个数。

基于标准Hamming 距离测度，下面定义直觉对偶犹豫模糊集的标准Hamming距离测度：

根据标准Hamming 距离测度，很容易给出直觉对偶犹豫模糊集的标准Hamming 距离测度这一定义，下证该定义满足定义5中距离测度的4个条件。

证明对于条件（1），因为f(x):X→[0,1]，g(x):X→[0 ,1]，所以 0 ≤ |fAσ(s)(xi)-fBσ(s)(xi)|≤ 1 ，0 ≤ |gAσ(s)(xi)-gBσ(s)(xi)|) ≤1 ，所以 0 ≤d(A,B)≤1，条件（1）得证。

对于条件（2），若A=B，显然d(A,B)=0，下证，若d(A,B)=0，则A=B。

因为d(A,B)=0，则必有d(hAσ(s)(xi),hBσ(s)(xi))=0 ，即|fAσ(s)(xi)-fBσ(s)(xi)|+|gAσ(s)(xi)-gBσ(s)(xi)|=0 ，所 以|fAσ(s)(xi)-fBσ(s)(xi)|=0 且 |gAσ(s)(xi)-gBσ(s)(xi)|=0 ，也 就是 说 ，fAσ(s)(xi)=fBσ(s)(xi) 且gAσ(s)(xi)=gBσ(s)(xi) ，所 以 ，A=B，条件（2）得证。

对于条件（3），显然，|fAσ(s)(xi)-fBσ(s)(xi)|+|gAσ(s)(xi)-gBσ(s)(xi)|=|fBσ(s)(xi)-fAσ(s)(xi)|+|gBσ(s)(xi)-gAσ(s)(xi)|，所以，d(A,B)=d(B,A) ，条件（3）得证。

对于条件（4），令：

因为，对任意的三个实数，x、y、z都有d(x,y)≤d(x,z)+d(z,y)成立，所以：

条件（4）得证。

由上述证明可知，基于标准Hamming距离测度，本文给出的直觉对偶犹豫模糊集的标准Hamming距离测度这一定义合理。下面给出其他距离测度。

基于标准Euclidean 距离测度，直觉对偶犹豫模糊集的标准Euclidean距离测度为：

基于加权Hamming 距离测度，直觉对偶犹豫模糊集的加权Hamming距离测度为：

基于加权Euclidean 距离测度，直觉对偶犹豫模糊集的加权Euclidean距离测度为：

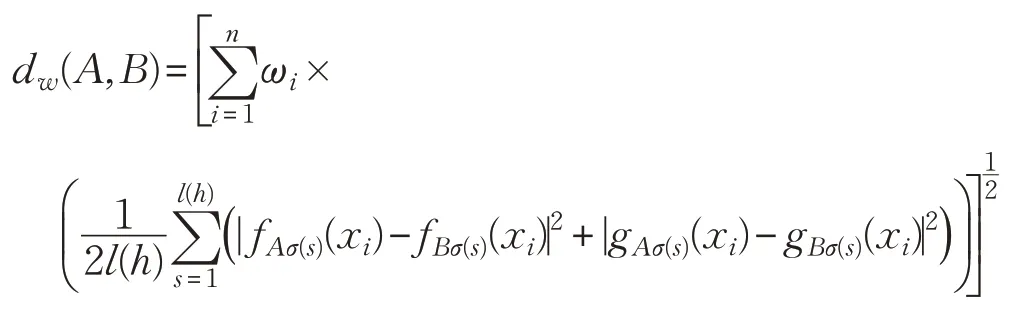
基于Hausdorff 距离测度，直觉对偶犹豫模糊集的Hausdorff距离测度为：

其中，fAσ(s)(xi)是fA(xi)中第s大的隶属度值，gAσ(s)(xi)是gA(xi)中第s大的非隶属度值。l(h)是直觉对偶犹豫模糊元hA(x)中实数对的个数。

4 直觉对偶犹豫模糊集的相关系数

定义6设A={＜x,hA(x)＞|x∈X}，B={＜x,hB(x)＞|x∈X}是固定集合X上的两个直觉对偶犹豫模糊集，称

为A和B的相关性指标。

性质1设A、B是固定集合X上的两个直觉对偶犹豫模糊集，则C(A,B)=C(B,A) 。

证明由定义6可知，显然，性质1成立。

定义7设A、B是固定集合X上的两个直觉对偶犹豫模糊集，称为A和B的相关系数。由定义6可知：

性质2设A、B是固定集合X上的两个直觉对偶犹豫模糊集，则R(A,B)为A和B的相关系数，则有下列式子成立：

（1）R(A,B)=R(B,A) ；

（2）0 ≤R(A,B)≤1；

（3）R(A,A)=1。

定义8设A、B是固定集合X上的两个直觉对偶犹豫模糊集，设权重信息为1,wk≥0，则称：

为A和B的加权相关系数。

5 直觉对偶犹豫模糊集的熵

定义9设M、N是固定集合X上的两个直觉对偶犹豫模糊元，如果F:X→[0,1]满足下列条件：

（1）当M={( 0,1)} 或M={( 1,0)} 时，F(M)=0。

（2）如果fM=gM，则F(M)=1。

（3） 对 ∀i，当fMσ(s)(xi)≤gMσ(s)(xi)时，有fNσ(s)(xi)≤gMσ(s)(xi)且gNσ(s)(xi)≥gMσ(s)(xi)；或当fMσ(s)(xi)≥gMσ(s)(xi)时，有fNσ(s)(xi)≥gMσ(s)(xi)且gNσ(s)(xi)≤gMσ(s)(xi)，则F(N)≤F(M)。

（4）F(M)=F(MC)。

则称F是直觉对偶犹豫模糊元M和N的熵。

设A是固定集合X上的直觉对偶犹豫模糊集，则构造A的熵为：

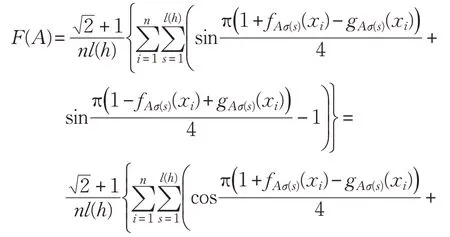
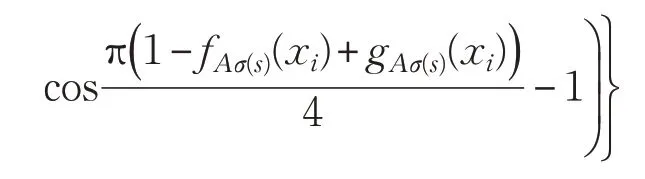
6 直觉对偶犹豫模糊集在多属性群决策中的应用

在多属性群决策中，由于人类认知能力有限，以及客观世界本身的不确定性，导致属性权重部分未知或完全未知。本文讨论在属性权重完全未知的群决策环境下，通过对直觉对偶犹豫模糊集的熵的定义，建立直觉对偶犹豫模糊集各属性客观权重模型，结合决策者的主观权重，得到各属性的综合权重。由于距离度量可以获得两个方案之间的差异性，而相关系数可以用来度量两个模糊信息之间的相关关系，因此本章基于理想方案与备选方案间的直觉对偶犹豫模糊集的距离测度、相关系数，提出一种新的多属性群决策方法。

令A={A1,A2,…,Am} 为备选方案集，E={E1,E2,…,En} 为属性集，将专家对各备选方案在各属性下的评价用矩阵T=(aij)m×n来表示，在直觉对偶犹豫模糊决策矩阵中，aij={(fAi(Ej),gAi(Ej) )}是一个直觉对偶犹豫模糊元，表示专家们对备选方案Ai在属性Ej下的评价。假设各属性的权重信息完全未知，且w={w1,w2,…,wn}且。

常见的赋权方法有主观赋权法、客观赋权法，但主观赋权会使得决策或评价结果具有较强的主观随意性，客观性较差，同时增加了对决策分析者的负担，在实际应用中有很大局限性。而客观赋权法没有考虑决策者的主观意向，有时会使确定的权重与人们的主观愿望或实际情况不一致，使人感到困惑。因此，本文选择将主观赋权与客观赋权综合起来，使用综合赋权法来确定各属性的权重。

因为熵Fj表示的是属性Ej中评价信息的不确定性程度，所以，熵值与对应权重的关系应该是Fj越大，Ej的权重越小，Fj越小，Ej的权重越大。所以，基于直觉对偶犹豫模糊集的熵，建立如下属性客观权重模型：

则客观权重为：a={a1,a2,…,an}

假设决策者对各个属性的主观权重为b={b1,b2,…,bn} ，则利用“加法”集成法可得wj=αaj+(1-α)bj(0 ≤α≤1)，其中wj表示第j个属性的组合权重，ai、bi分别为第j个属性的客观权重和主观权重，当决策者对不同赋权方法存在偏好时，α能够根据决策者的偏好信息来确定。

下面基于直觉对偶犹豫模糊集的加权Hamming距离，综合赋权法给出一种新的多属性群决策算法：

算法1

步骤1根据专家提供的决策信息构造直觉对偶犹家公司A={A1,A2,A3,A4} 的服务器可以进行选择，为选定的服务器考虑下面3个属性E={E1,E2,E3} 进行评估，其中E1代表“可带来的收益”，E2代表“迁移的成本”，E3代表“迁移容易程度”。

假设管理者们对属性的主观权重设置为b={0.4,0.4,0.2}，3位行业专家对各家公司在各属性下的评价构成直觉对偶犹豫模糊决策矩阵：

步骤2计算各属性的客观权重a={a1,a2,…,an} ，输入决策者对各个属性的主观权重为b={b1,b2,…,bn} ，以及赋权偏好α，最后，得到各属性的权重wj=αaj+(1-α)bj。

步骤3利用直觉对偶犹豫模糊集的加权Hamming距离测度公式，计算各备选方案Ai与理想方案A*={( 1,0)*}之间的距离测度d(A,A*)。

步骤4根据距离测度的大小，对各备选方案进行排序，距离测度越小，方案越优，反之，方案越劣，最后，选出最优方案。

下面基于直觉对偶犹豫模糊集的加权相关系数，综合赋权法给出一种新的多属性群决策算法：

算法2

步骤1根据专家提供的决策信息构造直觉对偶犹豫模糊决策矩阵。

步骤2计算各属性的客观权重a={a1,a2,…,an} ，输入决策者对各个属性的主观权重为b={b1,b2,…,bn} ，以及赋权偏好α，最后，得到各属性的权重wj=αaj+(1-α)bj。

步骤3计算各备选方案Ai与理想方案A*={( 1,0)*}之间的加权相关系数。

步骤4根据加权相关系数的大小，对各备选方案进行排序，加权相关系数越大，方案越优，反之，方案越劣，最后，选出最优方案。

下面给出一个例子对上述算法进行说明。

随着信息化时代的发展，某公司在生产销售过程中产生了大量的数据，并且分布在不同的服务器上，为了方便管理，企业管理者考虑采用云存储服务来将不同服务器上的数据进行集中，经过各部门初步筛选，现在有4

步骤1根据直觉对偶犹豫模糊决策矩阵，利用客观权重模型公式，计算各属性客观权重为a={0.376 6,0.284 8,0.338 6}，考虑主观权重为b={0.4,0.4,0.2} ，假设管理者对不同赋权方法存在偏好，即认为客观赋权的权重值占比40%，即α=0.4，因此，最终得到各属性的综合权重值为w={0.390 64,0.353 92,0.255 44}。

步骤2计算各备选方案与理想方案A*之间的加权 Hamming 距离：dw(A1,A*)=0.376 65 ，dw(A2,A*)=0.299 75，dw(A3,A*)=0.377 24，dw(A4,A*)=0.340 51。

步骤3 根据计算得到的加权Hamming距离可知，4家公司的排序为A2≻A4≻A1≻A3，从而利用算法1得出最优方案为A4。

按照算法2可知，通过计算各备选方案与理想方案A*之间的加权相关系数分别为：rw(A1,A*)=0.850 83，rw(A2,A*)=0.911 82，rw(A3,A*)=0.859 09，rw(A4,A*)=0.877 46，根据计算得到的加权相关系数可知，4家公司的排序为A2≻A4≻A3≻A1，从而利用算法2得出最优方案为A4。

从上述排序结果可以看出，虽然两种方法的评价方法不完全相同，但是最终选择却完全相同，也就是说，无论是基于距离测度，还是基于相关系数，直觉对偶犹豫模糊集均能很好地描述问题的模糊性与不确定性。因此，本文提出的新决策方法可以使决策结果更合理，具有有效性和可行性，具有更高的实用价值。

7 结束语

本文首先给出了直觉对偶犹豫模糊集的距离测度公式，其次给出了直觉对偶犹豫模糊集的相关系数、加权相关系数公式，并且讨论了相关系数具有的性质，然后给出了直觉对偶犹豫模糊集的熵的定义及其计算公式。最后给出了在属性权重未知的情况下，利用信息熵求属性客观权重的模型公式，再利用综合赋权法，求得了各属性的权重，然后分别给出了基于距离测度与相关系数的多属性群决策算法，并通过实例说明了该算法的有效性与可行性。