基于改进蚁群算法的三维航迹规划

魏 江，王建军 ，王 健，2，秦春霞，梅少辉

1.西北工业大学 电子信息学院，西安 710129

2.西北工业大学 第365研究所，西安 710129

1 引言

近年来，无人机航迹规划问题成为国内外学者研究的热点，尤其在军事、抢险救灾和测绘等领域尤为重要。为了提高无人机的生存机率并充分发挥其作战优势，必须选择一条能够快速安全到达目标且最大可能地完成任务并返航的航迹，因此航迹规划成为无人机相关研究中的重要内容。许多相关研究者将A*算法[1-2]、人工势场法[3-4]、概率地图算法[5]、遗传算法[6-7]、快速随机搜索树算法[8]等较为成熟的算法应用于航迹规划，这些算法在三维航迹规划中都存在一定的局限性。蚁群算法自从在著名的旅行商问题（TSP）和工件排序问题上取得成效以来，已经陆续用于解决车辆调度、路径规划、航迹规划等问题，该算法具备分布式计算、群体智能、正反馈等优点[9]，在三维航迹规划中有着广泛的应用[10-11]。

文献[12]在蚁群算法的启发函数中加入安全航行因素，使得无人机能够有效避开障碍，并且考虑了当前节点到目标节点的距离，提高了搜索的方向性，但是此算法在航迹规划初期，会消耗大量的时间。文献[13]针对蚁群算法在寻路初期需要大量时间来确定初始可行解的缺点，通过改变初始信息素的分布，提高了航迹搜索初始阶段的搜索效率，但是对算法整体的搜索效率提升相对较小。文献[14]对初始信息素分布和启发函数都进行了改进，但是对于复杂度较高的规划空间，仍存在收敛速度慢、拐点较多、航迹不平滑的问题，另外还会出现较多不必要的拐弯，使得无人机在飞行时会频繁地变更方向，不利于无人机飞行，本文在文献[14]的基础上提出了一种基于改进蚁群算法的无人机（UAV）三维航迹规划方法，改进了航迹规划的局部搜索策略和初始信息素调整因子，并在启发函数中加入路径偏移因子，降低了航迹规划空间的复杂度，提高了蚁群算法的搜索效率和收敛速度。

2 三维空间建模

在基于蚁群算法的无人机三维航迹规划问题中，大多数研究是针对较小的全局搜索空间（20×20 的网格）进行，网格分辨率一般为1 km[14-15]，这样规划的航迹精度太低。如果利用高分辨率DEM 数字地图（90 m 分辨率），20×20的网格只有1.8 km2，这与无人机实际的飞行范围相差太大，没有实用性，因此需要增加网格数量。文中利用90 m 分辨率的地图，网格数量扩大到100×100，也就是9 km2的地图中规划航迹。

2.1 空间划分

航迹规划空间被视为一个三维立方体空间ABCDEFGH，如图1 所示，在三维空间中建立直角坐标系O-XYZ，平面ABCD位于XOY平面上，A位于坐标原点。根据DEM的特性，可以将规划空间沿着Z轴方向划分成l（通过式（1）计算）个平面，每个平面又被划分为n×m的网格，这样规划空间被划分成n×m×l个网格。

其中Vc为无人机最大爬升率，V为无人机最小巡航速度，Δx为DEM 分辨率，z(i,j)为ABCD平面上每个网格对应的高度值，m和n由选取的DEM决定。

图1 三维空间划分示意图

2.2 局部搜索策略

无人机在三维空间中飞行节点的选取由约束条件确定，该约束一般包括：航迹距离、最小航迹段、最大拐弯角、最大爬升角等[16-17]。一般基于蚁群算法的航迹规划问题中，局部搜索空间为26个节点（三维）或8个节点（二维）且搜索步长固定为1[18-19]，这种搜索策略当全局搜索空间的栅格数量增加时，搜索时间就会大大增加。本文算法在DEM 数字地图中，根据无人机飞行节点的约束条件，确定搜索步长。

图2 所示为节点扩展图，在XOY平面内，A为无人机飞行航迹的上一个节点，O为当前节点，BCD为待扩展节点，被称作局部搜索空间，R为无人机转弯半径，假设A-O-B为已规划的航迹，由于无人机机动性能的约束，在E-O-F段的实际飞行轨迹为，因此最小航迹为2×|EO|，Ф为转弯角度，根据几何关系tan(Ф2)=|EO|/R，因此可得最小航迹为：

图2 节点扩展示意图

已知某无人机的最大转弯角度Фmax=45°，最小转弯半径Rmin=200 m，则最小航迹Lmin=165.67 m，DEM数字高程数据的分辨率为Δx=Δy=92.662 4 m，因此在一个平面内节点的选取分为图3（a）所示5种情况，箭头所指方向为飞行方向。根据不同的无人机参数和地形分辨率，可确定当前节点和待扩展节点的位置关系U与待扩展节点的集合V的映射关系为：

式中i表示当前节点与待扩展节点的位置关系情况个数。

图3 待扩展节点选取示意图

如图3（b），将待扩展节点沿Z轴方向扩展到三维，构成局部搜索空间。根据式（1），三维空间Z轴的分辨率与DEM 数字高程数据的分辨率有关，通过图3（a）所示的节点选择情况，如果当前节点在第k个平面，那么待节点只能在平面k、k+1、k-1、k+2和k-2内选取；局部搜搜空间节点个数为25 个，搜索步长为2，因此总体上减少可选节点的数量，从而降低航迹搜索空间的复杂度。

3 蚁群算法

给定图G=(V,A) ，其中V为顶点集，A为各顶点相互连接组成的边集，旅行商优化问题描述为求遍历所有顶点且距离最短的边集（每条边当且仅当出现一次）的集合[9]。蚂蚁依概率在各个顶点之间转移，在t时刻，蚂蚁k从城市i到城市j的转移概率为：

算法每完成一次迭代后，路径上的信息素将按照下式进行更新：

式中，τij(t+1) 为t+1 时刻蚂蚁在路径(i,j)上的信息素，ρ为信息素衰减系数；Δτij表示本次迭代中路径(i,j)上信息素增量，其初始值为零；表示上一轮结束的循环中第k只蚂蚁遗留在路径(i,j)上的信息素。

在Ant-Quantity模型中：

其中，Q为信息素常数，表示蚂蚁遍历一次所有节点所释放的信息素总量；Lk表示蚂蚁k遍历完所有节点后经历的总路程长度。

4 基于蚁群算法的三维航迹规划

蚁群算法的转移概率由信息素和局部启发式函数构成，两者将航迹长度作为评判标准。文献[20]提出的动态α和β权重，使初期以局部启发信息为重，后期以信息素为重。针对静态α和β权重，最有效的办法是改变初始信息素的分布和优化启发信息，在算法初期能够兼顾信息素和启发信息，在后期主要依据优化的启发信息，从而加快算法的收敛速度。

4.1 信息素表示

传统蚁群算法的初始信息素均匀分布，这样蚂蚁初始时刻在任意节点处选择航迹的概率相等，因此在算法执行的初始阶段，航迹搜索具有一定盲目性，会消耗大量时间，为此在航迹的起点和终点之间建立一条空间直线，通过三维空间中节点到该直线的欧氏距离的增加来改变初始信息素[13]，提高蚂蚁在初期的搜索效率。

图4 中比较了三种衰减函数对初始信息素的衰减情况。本文选用y=x-0.5对初始信息素进行衰减，因此初始信息素τ0可表示为：

图4 三种信息素衰减函数比较

其中，dijk为三维空间中节点到起点与终点连线的欧氏距离，为固定的信息素常数。

4.2 启发函数设计

启发函数是影响蚁群算法收敛速度和稳定性的重要因素，启发函数的设计直接影响着蚁群算法的性能。在单一航迹规划中，需要考虑安全性、航迹约束条件[21]。局部搜索策略中考虑了最小航迹段长度、最大拐弯角、最大爬升角，因此，启发函数中考虑了安全性和航迹距离，另外本文引入路径偏移因子，进一步约束无人机飞行节点的选择，使所选择的节点尽可能靠近起点和终点的连线上。因此本文引入安全启发因子、距离启发因子和路径偏移因子。

（1）安全启发因子

为了保障无人机的飞行安全，使无人机避开所有的障碍及威胁，本文引入了安全启发因子S。安全启发因子表示无人机的飞行高度是否大于三维地图的高度。通过式（8）计算：

其中，zk表示待扩展节点的高度，mapij表示待扩展节点对应于三维地图上的高度。

（2）距离启发因子

为了使规划的航迹最短，引入距离启发因子D。在图3（a）所示的待扩展节点的选取情况中，尽可能选取航迹最短的节点，但航迹最短的节点未必靠近终点，因此综合考虑当前节点到待扩展节点的距离|pi pi-1|和待扩展节点到终点的距离|pG pi|，所以D通过下式计算：

其中，w∈( 0,1) 。pi表示待扩展节点，pi-1表示当前节点，pG表示目标节点。

（3）路径偏移因子

如果只依靠距离启发因子约束航迹长度，航迹会有很多折点，有些研究中引入航迹平滑[15]，对折点进行平滑，以满足无人机的机动性，但是对于较大的拐弯，平滑效果不佳。本文引入路径偏移因子，让航迹上所有的点尽可能靠近起点和终点的连线上，减少拐弯。

在图5 中，假设起点为pS，p为搜索空间的一点，则p到直线l的距离M为：

图5 空间点线距离示意图

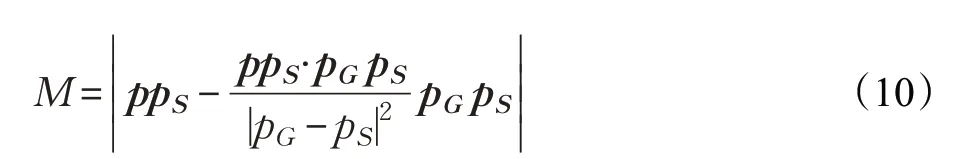
安全启发因子和距离启发因子的共同作用，能让无人机在三维全局搜索空间中选择安全无碰撞、全局航迹最优的节点；而路径偏移因子将节点约束到起点和终点的连线附近，平滑航迹，减少拐点和拐弯，加快搜索速度。因此本文蚁群算法的启发函数将综合以上三个启发因子：

4.3 信息素更新

本文采用局部信息素更新和全局信息素更新相结合的方式对信息素进行更新。

（1）局部信息素更新

每一代蚂蚁的个体经过一个节点后，对该节点的信息素进行衰减，保证其他个体有更大的机率访问其他节点，避免算法陷入局部最优。更新公式为：

式中，μ为信息素衰减系数，是一个介于(0,1)的参数，τ0是节点的初始信息素。

（2）全局信息素更新

一旦所有蚂蚁找到一条航路规划问题的可行解，必须对信息素做一遍全面更新[22]，更新规则如下：

式中，ρ表示信息素衰减系数，Δτijk表示所有蚂蚁在航迹上所有节点(i,j,k)的信息素增量，计算公式如下：

式中，表示第m只蚂蚁在节点(i,j,k)上的信息素，计算公式如下：

式中，Q为信息素常数，表示蚂蚁遍历一次所有节点所释放的信息素总量，Lm为一次迭代结束后的最优航迹长度。

4.4 算法步骤

改进蚁群算法的算法步骤如下：

（1）环境建模，首先将原始的DEM数字高程数据裁剪为无人机的实际飞行空间，导出.xyz 格式数据；根据公式（1）量化地图高度信息，将无人机的实际飞行空间构建成适合蚁群算法的航迹规划空间。

（2）初始信息素分配，根据公式（7），对均匀分布的初始信息素进行重分配。

（3）蚁群算法各参数初始化并将所有蚂蚁置于起点。

（4）根据公式（4）选择下一节点，根据公式（12）进行局部信息素更新。

（5）当所有蚂蚁完成一次迭代之后，根据公式（13）进行全局信息素更，否则返回步骤（4）。

（6）判断是否达到最短的航迹长度，若是，则输出最优航迹，否则，返回步骤（3）。

4.5 算例分析

为验证改进蚁群算法的可行性与有效性，本文采用PC 机（操作系统：Win10，CPU：i7-8750H，内存：8 GB），基于MATLAB 仿真平台进行对比实验。规划空间为101×101×44 的网格，分辨率为92.662 4 m，蚁群算法的参数在经典值范围选取：ρ=0.2 ，μ=0.2 ，α=2.5 ，β=4；蚂蚁个数m=50。

对于文献[14]蚁群算法和本文蚁群算法设置最大迭代次数为300 次，在9 种地形中分别进行50 次实验，50次实验的平均航迹长度如表1所示，图6为地形1、地形4和地形7中10次实验的搜索结果，图7为收敛曲线。

表1 航迹长度比较km

图6 蚁群算法搜索结果图

图7 收敛曲线图

从图6（a）、（b）、（e）中可以看出，文献[14]蚁群算法所规划的航迹在水平方向出现了很多拐点和较大的拐弯，这些拐点和拐弯在直观上是不必要的，这使得无人机在实际飞行过程中，会较多地变更方向，增加油耗且航迹并非最优；本文蚁群算法所规划的航迹基本沿着地形趋势，落在起点和终点的连线附近，基本没有出现明显的拐点和较大的拐弯，航迹比较平滑，说明在启发函数中的路径偏移因子的作用下，蚂蚁选择航迹的随机性降低，将选择的航迹节点约束到起点到终点的连线附近，从而减少拐点，使得航迹比较平滑；拐点的出现也说明当全局搜索空间增加时，文献[14]蚁群算法容易陷入局部最优，而本文算法全局寻优能力较强，避免陷入局部最优。从表1 的航迹长度比较可以看出，本文算法规划的航迹更短，在同样的迭代次数下，平均缩短24.08%。

从图7 中可以看出，虽然文献[14]蚁群算法在前20次迭代中，收敛比较快，但是整个收敛过程比较慢，当迭代到260 次时又出现了快速的收敛，因此收敛过程不稳定。本文蚁群算法在搜索的初始阶段，能够稳定较快地向最优解靠近，这是由于初始信息素调整因子的改进，结合路径偏移因子的约束，本文蚁群算法在收敛速度上有很大提升。50 次实验在9 种地形中的平均耗时如表2 所示，可以看出本文蚁群算法运行时间较文献[14]蚁群算法平均减少11.56%，说明改进的搜索策略发挥了重要作用，虽然在启发函数中增加了路径偏移因子，增加了算法的复杂度，但是总体上算法搜索效率有所提升，缩短了时间。表3 为最优航迹的节点个数，由于局部搜索策略的改进，本文算法所规划的航迹节点个数大约是文献[14]蚁群算法所规划航迹节点个数的一半，说明了本文蚁群算法搜索效率提升较为明显。

从图7 中可以看出，本文蚁群算法只要大约150 次左右就可以基本达到收敛，而文献[14]蚁群算法则需要迭代300次以上。为了验证文献[14]蚁群算法达到收敛条件时的迭代次数，认为最短航迹不再发生变化时，算法收敛完成，结果如图8，从图中可以看出，文献[14]蚁群算法需要迭代340次左右才能达到收敛。

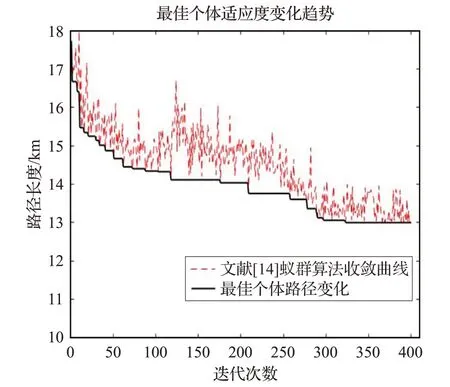
图8 文献[14]蚁群算法收敛曲线图

5 结束语

本文研究了基于蚁群算法的无人机（UAV）三维航迹规划方法，并对局部搜索策略、初始信息素调整因子和启发函数进行改进。在三维环境中进行的实验结果表明，本文蚁群算法搜索得到的航迹长度、收敛速度、时间效率和迭代次数比文献[14]蚁群算法都得到提高，在实际地形中能达到良好的航迹规划效果。航迹规划所面临的环境存在着复杂性和多变性，实际应用中靠一种算法很难得到理想的结果，因此多算法航迹规划有待进一步深入研究。

表2 平均耗时比较s

表3 航迹节点个数