无人机单目视觉AOA三维定位方法

熊 航，杨任农，梁晓龙，侯岳奇，王维佳

空军工程大学 空管领航学院，西安 710051

1 引言

无人机（UAV）小型化、自动化和机载计算等能力的提升使其近年来在各领域得到广泛应用。其中，无人机对目标的精确定位已经成为重要研究方向。计算机视觉（Computer Vision）技术的发展为无人机快速、精确地完成目标定位提供了可能[1]。

单目视觉（Monocular Vision）传感器具有精确度高，成本低，且数据信息丰富等特点[2]。将单目视觉与无人机相结合，学者开展了大量利用机载CCD（Charge-Coupled Device）摄像头进行目标定位的应用研究。文献[3-4]利用单目视觉实现了空中加油管锥套识别和三维定位，但算法依赖于加油管锥套的环形结构，对其他形状的目标不具一般性。文献[5]基于已知的农田和标志参数，利用无人机单目摄像头对农田飞艇进行定位，不仅需要先验信息且地形环境的变化会直接导致定位精度波动。文献[6]矫正无人机单目摄相图像的畸变后，根据参考物的尺寸完成了工地设施间的相对定位，但未完全反映三维空间的位置关系且需要已知的参考尺寸。以上特定场景的单目视觉三维定位，存在对先验背景信息依赖性强、定位精度受环境影响的问题。到达角（Angle of Arrival，AOA）定位[7]无需先验环境信息，且AOA定位精度只受传感器自身位置误差和量测基线角度偏差的影响。故基于AOA的无人机单目视觉定位为解决上述问题提供了新的途径。

AOA定位的主要难点在于量测数据和目标位置非线性相关，这对定位精度提出了较高的要求。文献[7-11]进行了提高二维平面AOA 定位精度的算法研究，但只适用于远距定位时忽略高度的情况，无法直接运用于三维定位。在精度需求较高的三维场景，AOA 三维定位的方向角和俯仰角耦合于非线性量测方程中，因此对算法提出了更大挑战。文献[12]运用工具变量（Instrumental Variable，IV）降低了三维定位偏差。文献[13]提出了一种旋转变量伪线性估计器（Rotation Variant Pseudolinear Estimator，RVPLE）利用传感器几何旋转角之间的关系减小三维定位的偏差。文献[14]提出了改进的IV 估计，通过减去偏差估计值来补偿偏差并取得了很好的效果。以上AOA三维定位算法均未考虑传感器自身位置的定位误差且AOA定位精度也与量测点的选取相关[15]。

以精确定位目标为任务背景，选取小型旋翼无人机平台，搭载CCD 云台相机，基于AOA 原理利用单目视觉量测参数进行定位，解决了传统单目视觉定位对先验背景信息依赖性强以及环境变化对精度影响的问题。首先建立了单目视觉针孔成像与AOA三维定位参数的量测模型。然后考虑无人机自身GPS 定位误差和角度量测误差，先完成目标二维坐标的伪线性估计（Pseudolinear Estimator，PLE），得出目标坐标的初步估计值以计算量测点与目标之间的距离，再代入三维伪线性方程通过加权最小二乘（Weighted Least-Squares，WLS）求解目标的三维坐标估计值。根据非等角分布选取量测点位置，设计旋翼无人机分时异地依次在规划的量测点上悬停并通过云台相机获取目标参数，实现了单目视觉的多点量测。最后，设计了无人机单目视觉定位的任务流程。仿真与实验部分验证了方法的有效性。

2 量测模型

AOA 定位中，目标与量测点连线的空间角度和量测点位置信息为定位所需参数。单目摄像机的成像模型解决了从图像中获取目标到达角的问题，无人机在量测点处的GPS 参数视为量测点的估计位置。角度与位置量测值均含噪声误差。

2.1 单目视觉量测模型

以相机光心为原点建立摄像坐标系Oc-XcYcZc，OcXc光轴与成像平面的交点o为像平面上图像坐标系原点，单个摄像机与目标成像关系如图1所示。

图1 针孔成像模型

根据针孔成像模型，目标p在图像坐标系yoz的像为Oc p连线与像平面的交点q，坐标为(yl,zl)。设Oc p在摄像坐标系中的方向角为θl（光轴为0°，顺时针为正），俯仰角为φl（水平为0°，向上为正），光心到像平面的距离为等效焦距f，由图1中几何关系可得[16]：

图像坐标(yl,zl)到像素坐标(ul,vl)转换公式为：

dy、dz为单位像素在坐标轴方向上的物理尺寸；u0、v0为图像坐标系原点o的像素单位坐标。式（2）代入式（1）得：

根据式（3），若已知ul、vl、u0、v0和等效焦距f与像元大小dy、dz之比，即可求得像素点在摄像坐标系中的方向角和俯仰角。

2.2 AOA量测模型

如图2 所示，单架旋翼无人机搭载CCD 云台相机，分时异地悬停于量测点，对目标进行N次成像拍摄。设在世界坐标系下，目标的真实坐标；将无人机和云台相机的实时位置视为重合一点，无人机位置坐标即为第i次量测点坐标，无人机真实位置，实际量测坐标由GPS 测量得出ui=[xi,yi,zi]T。N次测量无人机真实坐标实际量测坐标(u1,u2,…,uN)，定义坐标向量考虑GPS误差有：

图2 三维定位场景

Δu=是服从零均值高斯分布的随机向量，方差为，协方差矩阵为Qu。同时，定义U=[u1,u2,…,uN]T。

云台旋转角(θci,φci)是云台自身测量参数，目标成像角(θli,φli)通过式（3）获取，量测点的方位角θi=θci+θli和俯仰角φi=φci+φli即为两者之和。设角度真实值为和，则：

θ=[θ1,θ2,…,θN]T，φ=[φ1,φ2,…,φN]T为角度量测向量，为真实值；n=[n1,n2,…,nN]T，ω=[ω1,ω2,…,ωN]T是零均值高斯噪声，方差和协方差矩阵分别为。

式（4）、（5）、（6）即为AOA三维定位所需量测参数。

3 方法设计

利用量测参数，在三维坐标系中同时考虑无人机自身位置误差和量测角度误差进行AOA 定位，并基于Fisher 信息矩阵（Fisher Information Matrix，FIM）讨论定位过程中量测点选取的问题，最后设计无人机单目视觉定位流程。

3.1 三维定位算法

建立三维伪线性方程需要已知量测点与目标之间的距离di。故先进行二维方向的伪线性估计，得出目标坐标的初步估计值̂，求出距离估计值，再代入三维伪线性方程，运用加权最小二乘求得最终定位坐标，使其偏差最小。

3.1.1 二维伪线性估计

将无人机第i次测量处ui与目标的位置关系由三维投影至xoy平面，ui(1:2)取ui的前两个元素，得到关于目标实际二维坐标的伪线性方程[17]：

最小二乘解为：

通过算术平均得到z坐标：

式（8）、（9）的结果并未考虑量测噪声和无人机自身位置偏差，故其估计值只作为下一步三维伪线性方程中估算量测点和目标之间距离的条件使用。

3.1.2 三维加权最小二乘估计

在3.1.1 节的基础上，同时考虑角度量测噪声和无人机位置误差，定义：

建立三维伪线性方程：

其中，右式2N×3 矩阵G和2N×1 向量h分别为：

1 为全1向量，⊙为哈达马积，U=[u1,u2,…,uN]T。

左式中，ε=[nT,ωT,ΔuT]T，协方差矩阵Q=diag(Qn,Qω,Qu)；2N×5N矩阵R为：

其中：

为目标与量测点之间的估计距离，利用目标位置估计值̂与无人机位置量测值得出。运用加权最小二乘优化得到式的解：

其中加权矩阵W=(RQRT)-1。

3.2 量测点选取

AOA 定位精度不仅受定位算法影响，也与量测点选取有关[15]。设定无人机飞行高度不变，在水平面内选取N处量测点，则θi与的选取决定了所选量测点的空间位置。基于克拉美罗界（Cramer-Rao Bound，CRB）理论，平面内FIM矩阵J及其特征值det(J)可表示为：

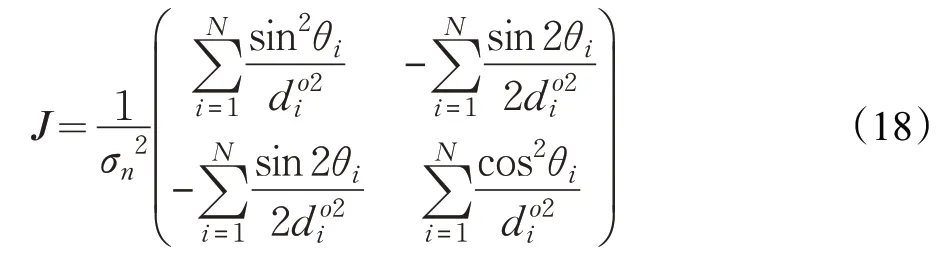
则CRB可表示为：

设目标函数为f(θ)且量测点与目标距离固定，使得CRB 最小的角度θi分布即为所选取的N处量测点分布。FIM最大特征值对应CRB迹的最小值，则优化问题转化为：

得出N处量测点的两种分布，等角分布（UAA）与非等角分布（Non-UAA）的角度关系分别为：

无人机在第i个量测点获取参数后，保持与目标距离不变，与目标连线角度分别偏转直至分别绕目标一周和半周后完成量测过程。

两种量测点选取均可得到最优分布[15]，但考虑非等角分布所需无人机飞行航时更短，因此选取Non-UAA进行定位，如图3所示。

图3 量测点分布

3.3 任务流程设计

根据量测点的分布选取和旋翼无人机平台CCD云台相机工作原理，设计基于AOA 的无人机单目视觉三维定位流程如下：

步骤1设置初始悬停点参数，载入无人机并发送指令，起飞升空至设定位置；

步骤2判断有无目标坐标的先验信息，若有，则转到步骤4；

步骤3在初始位置附近区域随机选取一组量测点，搜索识别目标进行量测，得出目标位置估计值；

步骤4依照非等角分布规划N处量测点坐标；

步骤5无人机飞行至下一量测点；

步骤6云台相机搜索识别目标，稳定悬停后，计算并记录角度参数θi、φi以及GPS定位参数；

步骤7判断是否飞行遍历所有量测点，若否，则转到步骤5；

步骤8将N组量测参数代入式（8）～（17），得到目标坐标定位值。

4 仿真与实验

为验证方法有效性，分别进行算法仿真与实验验证。仿真环境为i7-8565U，主频1.8 GHz，8 GB 内存，基于MATLAB 2017a环境代入实际参数进行仿真。实验平台主要组成为：飞行控制器、机载计算平台、通信模块、图传模块、云台相机和地面站。

4.1 算法仿真

设目标坐标为原点[0,0,0]T，在以原点为中心200 m×200 m×200 m 的立方体上半部分生成N处量测点坐标。设量测噪声均不相关，则所有协方差矩阵为对角阵，且无人机和云台相机的测量噪声方差在测量过程中的各量测点均相同。根据GPS 和云台相机设备出厂参数，取无人机位置测量噪声标准差σx=σy=0.5 m，σz=0.1 m ，角度测量噪声标准差σ=σ=0.2°。基于以上噪

nω声参数，以目标定位估计值与真实值之间的距离偏差为定位精度衡量标准，本节进行三组算法仿真：

（1）令量测点数量N=5，随机生成坐标，求取定位偏差均值，验证算法定位精度；

（2）改变量测点数量，随机生成坐标，求解量测点数量对定位精度的影响；

（3）量测点在水平面内非等角分布的坐标不变，改变量测点高度坐标，仿真求解最佳定位高度。

仿真1仿真次数1 至1 000 逐次设定，求解每组仿真次数下的平均定位偏差。

平均定位偏差随仿真次数变化情况如图4 所示。200 m×200 m×100 m 空间范围内的平均定位偏差在0.4～0.7 m浮动且逐渐收敛。

仿真2改变量测点数量N从2 到100，每组仿真1 000次。

量测点数量N变化时，平均定位偏差值的变化情况如图5 所示。随量测点数量增加，平均定位偏差由1.1 m 降至 0.2 m。其中，0～10 区间内趋势变化快，10～100区间内趋势平缓。考虑合理减少定位时长和数据处理复杂度，选取N=10 为实验参数。

图4 平均偏差收敛情况

图5 量测点数量对定位精度影响

仿真3设定N=10，在水平方向按图3所示的非等角分布取10 处量测点的坐标固定。改变量测点高度5 m至150 m，每组仿真10 000次。

量测点高度变化时平均定位偏差值变化如图6 所示。高度在50 m 以下时定位偏差保持在0.37 m 附近。50 m以上高度，随着量测点与目标高度距离增大，定位精度不断降低。综合考虑无人机实际飞行安全高度以及在定位偏差尽量小的情况下扩大搜索范围（即航拍视野），选取60 m作为量测点高度。

图6 无人机高度对定位精度影响

4.2 实验验证

如图7 所示，搭建四旋翼无人机为量测平台，地面站为控制处理中心。每处量测点悬停稳定时，GPS 信息、高度、航向角和机载云台角度信息以及云台相机对靶标的拍照图像实时发送至地面站的通信模块和数字图传并存储[18]。

图7 实验验证平台

10个靶标在150 m×50 m场地上分散布设，选取靶标1作为原点[0,0,0]T建立东北天（ENU）坐标系O-XYZ，得到所有靶标的位置关系如图8所示。

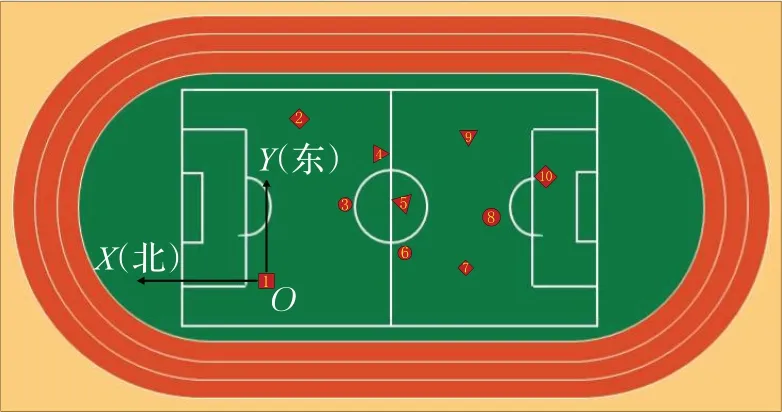
图8 靶标示意图

靶标的绝对坐标由差分GPS 测量，高度均设为0 m。真实坐标如表1所示。

考虑风力等天气因素对实验的影响，选择正午晴朗时分进行无人机飞行定位实验。根据4.1 节中的仿真结果，设定无人机飞行高度为60 m，初始位置在靶标群南向，量测点以半径为100 m 的半圆按非等角分布。云台相机采取跟随机头模式，故无人机航向角θc（正北为0°，顺时针为正）即为云台航向角，俯仰角φc（水平为0°，向上为正）由云台自身获取。无人机在10处量测点处进行搜索、识别、拍摄，通过图传和数传将图像与无人机的经度(lon)、纬度(lat)和高度(alt)信息传至地面站。

表1 靶标在东北天坐标系的真实坐标 m

表2 量测点坐标 m

表3 定位结果 m

采集图像中10个靶标的像素坐标，根据单目视觉模型求得靶标相对云台的角度信息θli、φli(i=1,2,…,10)，其中事先测定相机的等效焦距与像元大小比值参数为(3.68/3)×103。结合云台角度和靶标相对云台角度得到10处量测点相对靶标的角度。经无人机GPS和高度信息转换后，10 处量测点在O-XYZ中的坐标如表2 所示。将角度信息及表2坐标代入4.1节算法求得10个靶标的定位坐标，结果与真实值比较如表3所示。

如表3所示，对靶标的定位距离偏差最小为0.22 m，最大为1.37 m，平均为0.827 m。4.1节仿真中，量测点数量为10，高度为60 m情况下的平均定位偏差在0.37～0.4 m区间。实验取得了不错的定位效果。

与仿真结果相比，实验定位误差有所增大，可能与实际量测量过程中无人机GPS定位偏差较大、云台相机受环境不确定影响导致角度抖动过大，或者采集靶标的像素坐标过程中误差偏大有关。实际误差与仿真精度差异的根本原因在于实际量测过程中环境、人为因素带来的噪声误差协方差矩阵的不确定性，GPS和云台设备出厂参数与真实的无人机坐标量测误噪声Δu的协方差矩阵Qu以及角度量测噪声n、ω的协方差矩阵Qn、Qω存在偏差，导致最终计算的估计值与仿真结果有一定差异。

5 结束语

针对现有无人机单目视觉定位方法中对先验信息依赖和地形环境对精度影响的问题，提出了基于AOA的无人机单目视觉三维定位。建立了量测模型，采用二维伪线性估计基础上的三维加权最小二乘算法以及非等角分布量测点选取方法，设计了任务流程并进行了算法仿真与实验验证。设定条件下，算法仿真的定位距离偏差大约为0.37 m；实机实验中对靶标的定位保持在1 m左右，验证了方法的有效性，同时分析了实验与仿真之间精度差异的根本原因。

为减小定位方法的系统误差，后续计划开展以下工作：（1）改进AOA三维定位算法；（2）研究三维定位的最优量测点（最优构型）选取方法；（3）结合集群化思想，将无人机单目视觉分时异地的量测点定位方式拓展为无人机集群的多点、同时的协同定位，增加量测点数量并提高定位实时性。