基于Stackelberg安全博弈的动态防御策略选取方法

葛潇月，周天阳 ，2，臧艺超，朱俊虎，2

1.信息工程大学 数学工程与先进计算国家重点实验室，郑州 450001

2.国家数字交换系统工程技术研究中心，郑州 450001

1 引言

防御策略生成技术[1]通过分析潜在攻击威胁，评估安全态势，提供防御策略，对保障网络系统安全有重要意义。现有的防御策略生成技术常分为静态防御技术和动态防御技术。静态防御技术[2]是发生在攻击之后的一种被动防御技术。动态防御技术是通过态势感知、风险评估、安全检测等手段对当前网络安全态势进行判断，并依据判断结果实施网络动态防御。动态防御技术相比于静态防御技术能够实时识别网络中存在的脆弱点和潜在的安全威胁，从而达到提前规避风险的目的。网络攻防对抗的本质可以抽象为攻防双方相互博弈的过程，防御者所采取的防御策略是否有效，不仅要考虑自身安全需求，还应考虑攻击者可能采取的攻击策略和方法[3]。所以，基于博弈模型的防御策略生成方法相对于其他方法更能够体现攻防双方策略依存的关系，因此博弈模型在网络防御策略生成技术中应用广泛。

现有的基于博弈模型的防御策略生成技术可以分为静态防御策略生成技术和动态防御策略生成技术。在网络攻防对抗中，基于博弈模型的静态防御策略生成技术的研究已经十分成熟。文献[2]构建完全信息静态博弈模型进行防御策略生成，将网络对抗过程看成是双方拥有完全信息并同时采取行动的零和博弈过程，并给出了零和博弈算法。不足之处在于在网络对抗中使用完全信息静态博弈模型，与实际的应用场景不够贴切。文献[4]建立了不完全信息静态博弈模型对网络防御策略选取方法进行了分析，但文献中存在防御策略简单，策略收益量化仅为假设的情况。为解决收益的问题，文献[5]将网络所受攻击后的恢复时间作为收益来定义静态博弈模型，并分析网络安全性。上述文献都是基于零和博弈进行的策略分析，有些学者认为网络攻防行为可以采用非零和博弈进行策略的生成。文献[6]认为网络攻防行为中攻击策略和防御策略相互影响，在此基础上提出了一种基于博弈的网络安全态势感知方式，采用非零和博弈计算混合纳什均衡并给出了策略选取结果。但由于该方法对安全态势的定性分析较为片面，因此对于具体网络攻防策略生成的实施操作较为困难。

基于博弈模型的动态防御策略生成方法比静态防御策略生成方法能够更好地描述网络实时变化的情况。文献[7]在网络防御策略生成中引入动态博弈模型，基于动态博弈理论提出了完全信息和非完全信息两种场景的攻防博弈算法，进行策略的生成，但基于完全信息假设建立的博弈模型在现实攻防场景中很难满足。文献[8]在网络攻防对抗中提出了基于信号博弈的网络攻防博弈模型，从动态不完全信息的角度对网络攻防行为进行建模并给出信号博弈精炼贝叶斯均衡的求解过程。上述文献是基于单阶段博弈的策略生成技术。文献[9]提出了一种基于操作系统动态迁移的多阶段博弈模型，该模型是从攻击方出发得到最优策略。文献[10]基于不完全信息动态博弈构建的面向动态目标防御的单阶段和多阶段模型并给出了精炼贝叶斯均衡求解算法和先验信息修正方法，求解出不同安全态势下最优动态防御策略。文献[11]基于不完全信息动态博弈理论构建多阶段攻防信号博弈模型，解决了有限信息条件下，多阶段网络防御策略选取问题。但在对主动防御机制进行研究时主要考虑了信号的选取和释放方式，并没有考虑到其他的防御机制。在安全态势评估的过程中文献[12]提出了基于马尔可夫博弈模型的风险评估方法，该方法考虑了双方行为对风险的影响，动态地分析了潜在风险，文献在安全态势评估与预测子系统中进行了实现。

通过上述分析发现，基于博弈模型的防御策略生成技术虽解决了网络中攻防双方目标对立、策略依存和关系非合作性质的描述，但无法刻画攻防双方的信息不对等特性。

本文将Stackelberg 安全博弈[13]引入到网络攻防的过程中来解决攻防双方信息不对等问题，进而得到最优防御策略。首先分析网络攻防过程中攻防双方的信息不对等特性；依据攻防双方策略交互的竞态特性，构建了基于Stackelberg安全博弈模型的安全策略计算模型，并利用了该模型求解网络防御中的最优防御策略；最后通过仿真实验验证并分析了该方法的有效性。

2 相关知识

2.1 Stackelberg安全博弈

Stackelberg博弈模型在20世纪30年代被提出，用于竞态条件下的最优策略生成[14]。如图1所示，Stackelberg安全博弈模型主要包含领导者L和跟随者F，L和F有各自的策略集合。L和F分别根据自身的策略在动作集合中选取动作a和d在环境中执行。L和F会根据环境的变化情况调整自身的策略。当L或F在执行策略时，只有一个动作，则称为纯策略，有多个动作且每个动作被选择的概率为[0，1）时，则称为混合策略[15]。在Stackelberg安全博弈中领导者首先确定自身的混合策略，跟随者通过观察得到领导者的策略信息，然后选择能够最大化自身收益的策略进行博弈，根据策略执行动作跳转到下一状态。

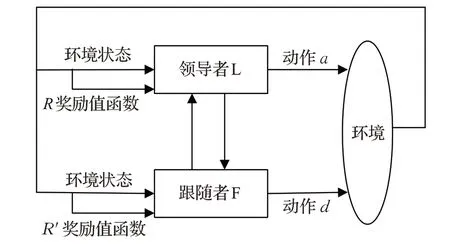
图1 Stackelberg安全博弈模型

在Stackelberg安全博弈[16]中，用x={xt}表示领导者的策略，其中xt是目标t的覆盖概率，可行策略集合是X={0 ≤xt≤1}。当跟随者发起攻击时，领导者没有对目标t进行保护，则跟随者得到奖励为，领导者得到惩罚为。当跟随者发起攻击时，领导者对此目标t进行保护，则领导者得到奖励为，跟随者得到惩罚为。根据收益向量[17](Ra,Pa)和(Rd,Pd)，得到跟随者的预期收益(x,Ra,Pa)和领导者的预期收益(x,Rd,Pd)：

Stackelberg 安全博弈是在同时考虑领导者和跟随者策略的情况下，最大化领导者收益的策略游戏。

2.2 马尔可夫决策过程

马 尔 可 夫 决 策 过 程[18（]Markov Decision Process，MDP）是基于马尔可夫理论的随机动态系统的最优决策过程。MDP可以表示为一个五元组(S,A,T,γ,R)，其中每个元素的定义如下：S为决策者在所处环境中所有可能状态的有限集合。A为决策者能够采取的动作集合。T(s,a,s′)∈[0,1]为当前状态到下一状态的转移概率函数。γ∈[0,1)为折扣因子，可以保证无限步长的情况下回报的收敛性。R(s,a,s′)为回报函数，防御者在状态s中采取动作a获得回报。马尔可夫决策过程的目标是获得最大化期望的长期回报。为评估智能体策略，需要状态-值函数。当智能体从状态s开始并随后执行策略π时，在该策略下状态s的状态-值函数Vπ(s)定义为预期回报。

式（3）中T(s,a,s′)表示在当前状态s和行为a时，转移到下一状态s′的概率，而R(s,a,s′)为当前状态s和行为a下在状态s′所得到的预期直接回报。一个最优策略π*将使得智能体在所有状态下获得最大化的折扣未来回报，从而使得：

若智能体从状态s开始并执行最优策略π*，则可获得最优状态-值函数Vπ*(s)。

动作-值函数Qπ(s,a)可定义为在状态s选择了特定行为a之后，并执行策略π而得到预期回报。在终止状态时，状态-值函数总为0，从而使得动作-值函数也总为0。动作-值函数Qπ(s,a)如下：

3 基于Stackelberg安全博弈的动态防御策略生成

本章首先对网络模型进行形式化定义，说明模型的合理性，在给定的模型中使用Stackelberg安全博弈动态生成防御策略。

3.1 Stackelberg安全博弈模型在网络攻防场景的适用性说明

在网络场景中攻击者和防御者对于网络信息的了解程度不同。防御者首先通过部署安全策略对网络环境进行保护，攻击者通过探测确定网络状态进而实施攻击。网络场景信息通常包括：网络连接情况、操作系统类型、端口信息、漏洞信息、主机上的应用和基础设施等。

（1）防御者对于自身的端口信息、操作系统类型、网络连接情况、主机上的应用和基础设施等网络信息的掌握程度有先天优势而攻击者只能通过扫描等操作对网络进行探测，推断防御方的安全部署情况。所以在网络场景中防御者对于场景信息的掌握程度要优于攻击者。

（2）在漏洞信息大多数是公开的情况下，由于防御者掌握着操作系统类型和主机上的应用等信息，所以相对攻击者来说，防御者对网络中的漏洞掌握情况要优于攻击者。

（3）在网络场景中，防御者部署安全策略需要花费成本，防御者的目的是使用最小的成本最大程度地保护网络的安全。

本文为体现攻防双方在网络攻防过程中信息不对等特性，将防御者定义为网络环境中的领导者，攻击者定义为网络环境中的跟随者。所以Stackelberg 安全博弈领导者-跟随者模型适用于网络攻防过程。

3.2 Stackelberg安全博弈的模型构建

本文在模拟网络环境时使用马尔可夫决策过程对网络环境进行建模。其中MDP的五元组(S,A,T,γ,R)，在此模型中的定义如下：

S，在状态集合S中，每个状态都是攻击者和防御者所处网络环境中可能存在的状态。网络环境中的状态为网络实体上的特权状态，分为无任何特权、远程访问特权、本地用户特权和根特权四种。

A，网络模型中动作集合为防御者和攻击者的所有动作集合。攻击者动作为网络中存在的弱点信息。防御者动作为防御策略库中选取的防御动作。

T(s,a,s′)∈[0,1]，转移概率函数描述了攻击者和防御者在当前状态s下进行动作a，到达下一个状态s′的概率，转移概率函数模拟了动作的随机效应。这里的状态转移为网络实体上的特权状态变化，可以是单个节点上的权限提升也可以为网络的横向提升。在典型的攻防场景中，防御者在当前状态采取防御动作跳转到下一状态，如果在网络环境完全清楚的情况下则转移到的状态也是一定的，但在许多决策的过程中动作效果并不一定，这样在状态转移的过程中就具有随机性。状态转移函数具有马氏性，可形式化描述成：

γ∈[0,1)，在网络模型中，防御者进行策略选取时，当取γ接近于1的情况下，说明了防御者在进行策略选取的时候更关注于长远的回报。

R(s,a,s′)，在网络模型中将易被攻击的节点设置成较大的正数。本文使用的回报值是参考漏洞的评分机制[19]来进行定义。

3.3 基于Stackelberg安全博弈的动态防御策略选取算法

在Stackelberg 安全博弈中攻击者的目标是成功攻击潜在主机，攻击者完成攻击任务后能够得到较大收益。攻击者在完成攻击任务后可继续对下一个目标进行攻击。防御者的目的是对潜在主机进行保护，防御者在攻击者对目标主机进行攻击之前对于被攻击主机进行有效防御才能够获得较大收益，视为防御成功，否则视为失败。

本文中防御者的动作空间为Adef，攻击者的动作空间为Aatt。当防御者选择行为d∈Adef，攻击者选择行为a∈Aatt时，攻击者收益的最大值定义为攻击者的最优响应函数RF(d)：

式中，为防御者与攻击者策略组合为＜a,d ＞时攻击者的收益值，这里可以同上文中的动作-值函数等价。＜d*,RF(d*)＞为Stackelberg 的均衡策略。在Stackelberg均衡策略中，博弈双方具有先后顺序选择策略。当领导者在进行策略选择时，得到双方收益最大化的策略，双方不能够通过单独调整自身策略来得到更高的收益。但如果出现多个策略对于跟随者来说没有区别的情况，最优响应可能不唯一，这时需要在Stackelberg 均衡策略的基础上计算Stackelberg 强均衡策略。在Stackelberg强均衡的情况下，当跟随者有多个策略收益相同时，总是选择对领导者最有利的策略[20]。Stackelberg 强均衡策略是所有Stackelberg 均衡策略中最大化领导者收益的策略。

在求解攻击者最优响应集合时，式（6）中转移概率函数T(s,a,s′)完全已知，那么最佳策略可通过动态规划算法[18]获得。但在本文场景应用中，智能体所处的网络环境中T(s,a,s′)是未知的，在此情况下不能通过动态规划算法计算最优策略。式（8）可通过式（9）迭代得到，从式（9）中可观察到并没有使用概率函数T(s,a,s′)。

本文需要考虑到的是多智能体的动作-值函数Q*(s,a1,a2,…,an)，这里以两个智能体为例：

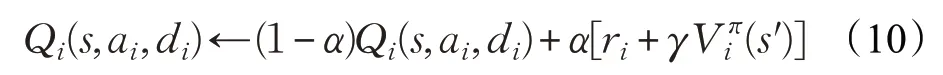
式中，di表示智能体ai的对手，Qi(s,ai,di)为智能体i和对手分别选择行为ai∈Aatt和di∈Adef时的预期回报。

通过式（10）得到攻击者的动作-值函数Qatt*(s,ddef,aatt)，其中ddef为，是防御者的行为集合，是攻击者的行为集合。在状态s下，计算防御者每种行为对应的攻击者最优响应行为集合RF(ddef)。

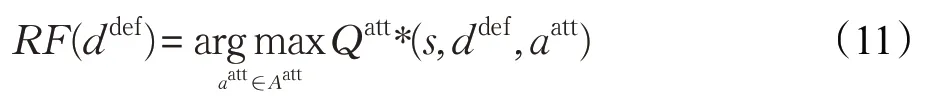
通过式（11）从攻击者最优响应行为集合中找到一个能够最大化防御者收益的攻击者行为。

式中防御者的动作-收益函数Qdef同样是根据式（10）得到的。最后根据式（13）得到状态s下防御者的最优策略。

最终得到结果是确定状态s下得到的防御者最优策略，如算法1 所示。该算法在t=0 时刻，初始化每个智能体的Q值。在以后任意t时刻，防御者通过观察周围的环境得到最大化自身收益的动作，实现最优防御策略的选取。算法中用来表示根据每一个状态-动作对求解均衡的过程。

算法1

该算法核心为利用状态-动作对求解均衡策略的过程。在模型中攻防状态集合可扩展到n，攻防策略集合同样也可以扩展到n，说明本文的模型具有较好的通用性。将本文方法与其他文献中的方法进行对比，本文采取动态博弈的方法，相比采用静态博弈的方法，能够充分地考虑到攻防双方行动的非同时性，更加符合实际需求；Stackelberg 安全博弈相比于单阶段博弈，考虑了攻防双方在博弈中信息变化的情况，更加贴近实际攻防场景；基于Stackelberg安全博弈的策略选取方法考虑到了攻防双方在博弈的过程中信息不对特性，规避了网络防御策略研究中攻防博弈双方主体地位对等的先验假设缺陷，更加贴近攻防实际情形。

4 实验

4.1 实验设置

为验证前面所提出的基于Stackelberg 安全博弈强均衡策略算法能够生成最优防御策略，建立如图2 所示的网络拓扑结构来模拟网络攻防场景。实验采用python作为主要的开发语言，实现了控制脚本和仿真场景运行。该实验场景中，攻击主机位于外部网络，目标网络为交换网络，其中三台计算机分别为数据库服务器、文件服务器和Web服务器。安全防御规则限制外部网络对目标网络的访问请求。攻击者在攻击主机上具有root权限，攻击者的最终目的是获取数据库服务器的root 权限。根据防火墙规则如表1 所示，攻击者在Web服务器和文件服务器上都有访问权限，但对数据库服务器却没有访问权限。Web 服务器和文件服务器在数据库服务器上具有访问权限，这样攻击者可以根据服务器之间存在的依赖关系获取数据库服务器的访问权限。

图2 实验场景

表1 防火墙规则

攻击策略如表2所示，主要根据攻击复杂度和漏洞评分综合考虑得到，攻击策略收益如表3所示，防御策略为其对应的补丁。为简化实验场景单纯以漏洞来说明攻击有效性，越是高危的漏洞，危险级别越高。防御策略收益如表4 所示。防御策略收益表中的影响是根据国家信息安全漏洞共享平台中给出的危害级别中的漏洞评分参考而来的，成本是根据攻击的复杂度给出的。

表2 攻击策略

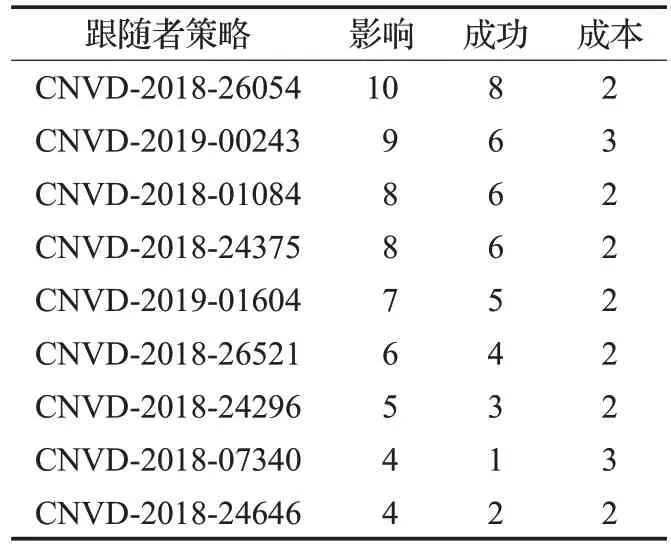
表3 攻击策略收益

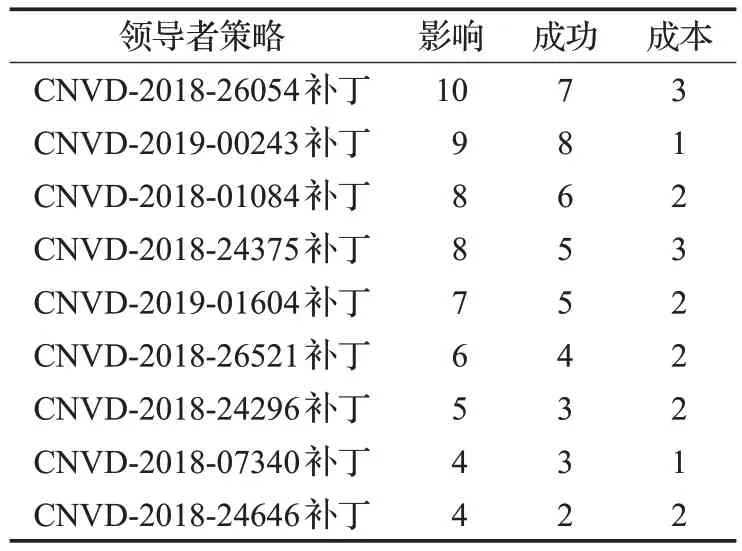
表4 防御策略收益

4.2 实验结果及分析

根据表3 和表4 的数据，如果修补手段对于攻击手段是有效的，那么防御者获得收益为防御者的行动影响减防御者的成本，攻击者的收益是其攻击手段的成本；如果修补手段对攻击手段是无效的，那么防御者的收益为防御者的成本减攻击者的攻击影响，得到的收益为负数，攻击者的收益为攻击者的行动影响减攻击者的攻击成本[21]。以此得到攻防收益矩阵如表5所示。利用基于Stackelberg 安全博弈的动态防御策略选取算法，得到防御策略可见，防御者的最优防御策略为CNVD-2018-26054补丁，次优防御策略为CNVD-2018-01084补丁。在实际应用中可以根据网络环境、网络安全需求，以及成本等因素来进行防御策略的选取，领导者可以使用混合策略，这样能够加强网络系统的安全性，达到更好的防御状态。

表5 收益矩阵

为证明采用Stackelberg均衡策略的必要性，将本文提出的方法和其他文献进行对比，详见表6。与本文对比的三个文献中包含了完全信息博弈和不完全信息两种博弈类型，单阶段和多阶段博弈两种博弈过程。选择不完全信息静态博弈文献[4]与本文进行对比，发现在利用上述博弈场景的情况下，基于场景模型的不完全信息静态防御策略选取算法，得到最优防御策略的均衡：即防御者的最优防御策略是以概率选择CNVD-2018-01084补丁，以概率选择 CNVD-2018-26054 补丁，以概率选择CNVD-2019-00243 补丁。通过实验结果的对比可以看出Stackelberg 均衡策略是以最高概率选择CNVD-2018-26054 补丁，次高的概率选择CNVD-2018-01084 补丁，以最小概率选择CNVD-2019-01604 补丁。文献[4]则是以最高的概率选择CNVD-2018-01084 补丁，以最小概率选择CNVD-2019-01604 补丁。与国家信息安全漏洞共享平台[19（]CNVD）中的安全研究情况对比CNVD-2018-26054补丁相比于CNVD-2018-01084补丁对网络场景安全维护更加有必要。在有限成本的情况下进行最优防御策略的选择时，Stackelberg均衡策略相比于文献[4]中的均衡策略能够更加有效地对网络系统进行防御，因此Stackelberg均衡策略更加符合。对比实验结果表示采用Stackelberg 均衡策略在网络攻防动态防御策略选取是必要的。

表6 对比实验

5 结束语

本文首先分析在基于博弈模型的网络安全防御技术的研究中并没有考虑到网络攻防双方之间信息不对等的关系，提出了基于Stackelberg安全博弈的动态防御策略生成方法。实验结果表明本文提出的算法能够为网络进行有效的防御提供参考。

本文的后续工作将围绕以下几个方面进行：一是扩展网络模型，解决部分可观测模型的构建问题；二是算法的可扩展性，提升算法的适应范围。