基于深度自编码的多视图子空间聚类网络

郭 圣，仲兆满，李存华

1.中国矿业大学 计算机科学与技术学院，江苏 徐州 221000

2.江苏海洋大学 计算机工程学院，江苏 连云港 222005

1 引言

子空间聚类是机器学习、计算机视觉和模式识别的基础课题之一，例如图像表示、人脸聚类和运动分割[1-2]。子空间聚类的重要性在大量文献中得以体现，因为它是通过数据分析从子空间推断数据结构信息的关键步骤[3]。子空间聚类的目的是将从多个低维子空间中提取的数据点分割成不同的聚类。

在现实的应用中，样本中的数据通常都是高维的[4]，因此许多聚类技术也面临维度灾难的挑战，为了充分处理这些高维的样本数据，一个合理的方法是检测并使用这些样本的底层子空间结构。大量研究表明，这些高维数据的内在维度通常远小于实际维度[5]。因此，子空间聚类技术近年来受到了广泛的关注。近年来提出了许多子空间聚类方法，例如稀疏子空间聚类（SSC）[2]、低秩表示（LRR）[1]。为了提高原始SSC 或基于LRR 的方法的鲁棒性和表示能力，研究者们还提出许多改进方法，例如结构化稀疏子空间聚类（S3C）[6]、图正则化低秩表示（LRRGR）[7]和潜在低秩表示（LLRR）[8]等子空间聚类方法。S3C 将每个数据点表达为所有其他数据点的结构化稀疏线性组合，并同时学习相似性和分割性。LRRGR和LLRR利用流行正则化项来保留数据的局部几何结构，提高原始模型的表示能力和子空间分割精度。虽然在单视图数据（由一个视图组成的数据）上这些子空间聚类方法取得了较好的性能，但这些方法具有以下限制。首先一个挑战性的问题是这些方法采用线性假设，基于这种情况利用凸方法可以很好地解决子空间聚类问题，但是在现实中，数据之间的关系通常是高度非线性的，上述方法可能会降低聚类性能。其次随着如今对数据信息化的要求越来越高，特定信息和通用信息在数据中共存，仅从单一视图描述数据已无法得到预期效果。

在当今数据爆炸时代，通常获得的数据具有多个视角（对事物不同的特征描述），即多视图数据。相比单视图数据，从多视图数据中可获得丰富的信息。因此多视图数据的子空间聚类问题成为学者们的研究重点。对于多视图数据子空间聚类来说需要利用来自多个不同数据特征中所挖掘的综合信息，即互补性和一致性，如图1 所示。最近，Cao 等人提出多样性诱导的多视图子空间聚类（DIMSC）[9]。此方法从不同的角度探索不同视图的互补信息，利用希尔伯特-施密特独立准则（HSIC）从不同的角度学习不同的子空间，可以解决数据相对复杂的依赖性。然而使用HSIC 的缺点是HSIC是一个值感知标准，由于规模问题值感知正则化可能会降低了其性能，而且DIMSC 在两个分离的阶段中执行子空间学习和谱聚类，不能充分地保留公共聚类结构。Wang 等人为了克服上述缺点提出了排他性-一致性正则化多视图子空间聚类（ECMSC）[10]，在此方法中使用位置感知准则处理元素值大小，并将两个分离的步骤（即子空间学习和谱聚类）合并到一个优化框架中，利用补充信息的排他性和一个指示器的一致性来统一处理子空间聚类，但是此方法构建的相似性信息量较少而且也缺乏利用不同视图之间的多样性，无法揭示不同视图的子空间结构。Gao 等人为了确保不同视图之间的一致性提出了多视图子空间聚类（MVSC）[11]，这种方法对每个视图执行子空间聚类，采用了一个共同的指标来保证共同的集群结构，强制使不同视图中的点被分类到同一集群中。但是这个算法忽略了每个视图的局部结构，仅仅拼接多视图数据中的特征并执行子空间聚类，无法利用数据的内在特征。朴素多视图子空间聚类（NaMSC）方法首先使用Hu等人提出的平滑表示聚类（SMR）[12]从每个视图中学习子空间表示，然后将谱聚类应用到学习表示的框架中，NaMSC 仅直接组合多视图表示并独立地学习每个子空间表示，因此无法保证不同视图的互补性。这些方法虽然取得了不错的聚类结果，但还是存在上述问题。目前多视图聚类方法大部分基于浅层聚类模型，因此对于复杂数据结构很难学习鲁棒表示。

图1 多视图学习示意图

在深度学习领域中，自编码器作为另一种流行的复杂数据表示方法，引起了研究者们的关注。Hinton等将自编码器作为一种降维方法使用在深度定向网络中，改善了数据局部极小的问题[13]。Vincent P 等将自编码器应用于图像的降噪[14]，能够强迫网络学习到更加鲁棒的不变性特征，并获得较好的结果。Krizhevsky用自编码器编码图像，在目标分类问题上取得了巨大的成功[15]。自编码器在其优化发展过程中，被广泛应用到模式识别、自然语言处理、图像分类和聚类以及其他领域[16]。为了提高多视图复杂数据子空间聚类算法的学习效率，本文将子空间学习引入到深度自编码模型中，提出一种基于深度自编码的多视图子空间聚类网络（DMSCN），该网络能够表示多视图数据中非线性结构，且有效地从多视图中提取多层子空间。在模型中利用加权稀疏表示，并保证数据的局部性，进而提高了学习效率。最后实验表明，在常用的多视图数据集上，提出的模型优于其他先进的多视图子空间聚类模型。

2 深度子空间聚类网络

2.1 浅层自编码器模型

自编码器是一种无监督的数据维度压缩和数据特征表达方法[16]。在自编码器中，通过不断训练网络中的参数，就可以将网络中的权重初始化到一个比较好的位置，经过这样的多重训练可以得到信息的多重表示方式。一般自编码器的结构如图2所示，自编码器的目标函数（1）如下所示：

自编码器分为浅层自编码器和深层自编码器，浅层自编码器分别有一层编码器和解码器，深层自编码器则有多层编码器和解码器。以浅层自编码器为例：

（1）编码器部分，其实现了数据的压缩，对于输入X：

图2 浅自编码器网络结构

其中，W1是连接输入层到中间隐层的权重矩阵，p1是编码器的偏置向量。sJ(⋅)为输入层和中间隐层之间的激活函数，一般选取为sigmoid函数，即。

（2）通过解码器部分将编码h映射到原始数据维度上，即对数据的复现：

其中，W2是中间隐层到输出层的权重矩阵，p2是解码器的偏置向量，g(⋅)为解码器激活函数。通常选取为sigmoid函数或恒等函数，恒等函数即g(x)=x。

从式（2）和式（3）可以看出，自编码器每一层的训练都是独立的，通过尝试重建前一层中的表示来捕获更抽象的特征。在训练过程中寻找参数集，重构输入数据，使得输出层输出的数据与输入层输入的数据尽可能接近，即输出数据与输入数据的误差尽可能小。这里损失函数可以有两种形式，（1）平方误差损失函数，即式（4）。（2）交叉熵（cross-entropy）损失函数，即式（5）。

在训练中，通过优化平滑函数（通常是欧几里德范数）来学习编码器和解码器，结合式（2）到式（5）可得目标损失函数为：

其中，LS项中Lζ表示交叉熵损失函数LCE或是平方误差损失函数LMSE。另外ng表示神经网络的层数，sg和sg+1分别表示第g层和第g+1 层的元素数目，λ为权衡参数。

2.2 深度子空间聚类网络模型

前面着重介绍了浅层自编码器模型，在本节中将进一步介绍加入重建关系的自编码器——深度自编码器网络模型。在流形学习中，假设某些属性对不同的投影空间是不变的，因此可以通过将输入空间中的特定属性保留到另一个空间来学习表示。这种表示是寻求不变性，在文献[17-18]中已表明其有效性：假设数据由N个实值向量Si组成，每一个维度都是从某些潜在的流形中采样。若有足够的数据，则期望每个数据点及其邻近点位于或接近流形的局部线性块上，可以用线性系数从相邻的数据点重建每个数据点，进行描述这些块的局部几何特征。这里重建误差用损失函数（7）来衡量：

其中，权重Wij表示第j个数据点对第i个数据点重建的贡献。使重建误差最小化的约束权重遵循一个重要的对称性：对于任何特定的数据点，它们对该数据点及其相邻点的旋转、重定线和转换都是不变的。在本文中重建关系可以认为是不变性的类型。这种关系可以保证数据的全局结构，此网络中引入一种已证明在传统子空间聚类中有效的自我表示特性。通过这种方式可以学习所有数据点之间的成对相似性，并产生样本亲和度矩阵和子空间聚类结果。

其中，||·||F表示Frobenius范数，λ为权衡参数。因此可以利用C来构建用于谱聚类的亲和度矩阵。

在大多数现有的子空间聚类方法中，每个样本都被编码为整个数据集的线性组合。与线性子空间聚类模型不同，深度子空间聚类网络可以学习多个非线性变换将样本输入映射到另一个子空间中，从而可以将获得的低维表示与非线性表示相结合，同时适应局部和全局子空间结构。特别是该网络以最小的重建误差来学习输入数据的表示，确保数据的固有局部性结构。深度子空间聚类网络模型构建如下[19]：

其中，R(S)表示编码器的输出，||R(S)-R(S)C||表示自我表示项，̂表示由自编码器输出的数据。在此网络中将每个数据点作为网络中的一个节点，并将每一个数据点通过权重与其他点的加权线性组合来近似计算，可以通过一个线性全连接层来表示自我表示项。相比于传统的自编码器，深度子空间聚类网络模型不仅适用于无监督子空间聚类，可将输入的数据非线性映射到潜在空间，在模型中引入传统子空间聚类中自我表示特性，表明其关系对于不同的特征空间是不变的，进一步揭示数据的相关性；而且该网络从深度学习模型的不同层收集视图的补充信息，使得它能恢复更准确和稳定的聚类结构，以获得更好的聚类结果。

该网络算法主要描述为如下过程：

（1）如式（2），X作为输入数据进行前向反馈运算，根据式（3）得到输出Y。

（2）根据式（9）得到函数损失值。

（3）进行后向反馈运算，利用随机子梯度下降法算法优化损失函数。

（4）重复步骤（1）到（4），直至损失函数收敛。通过上述算法步骤可以得出自表示系数矩阵。

3 深度自编码器的多视图子空间聚类网络模型

3.1 问题设置

首先，解释以下一些符号表达。B表示矩阵，b表示向量，tr(B)表示矩阵B的迹，BT表示矩阵B的转置矩阵，(B)ij表示矩阵B中第i行j列的元素，bj表示矩阵的第j列向量。

现实中的数据通常为多视图非线性数据。若采用传统线性聚类方法针对这类数据进行聚类，既不能有效表示数据非线性结构又不能充分利用多个视图信息，从而导致聚类效果往往不够理想。虽然深度子空间聚类网络能够表示数据中非线性结构，但是该网络不能保证所学习的矩阵具有一致性和原始数据的相似性信息，导致性能不佳。为了解决上述问题，本文提出一种基于深度自编码的多视图子空间聚类网络（DMSCN）。

3.2 深度自编码的多视图子空间聚类网络

在本节中将详细介绍基于深度自编码的多视图子空间聚类网络（DMSCN）。图3 说明了DMSCN 的基本思想，具体说明为：（1）DMSCN是一种多层非线性网络模型，具有捕获数据非线性的能力。（2）DMSCN通过自表达层H(N2)提取数据中的特性进行编码，保证了数据的全局性。（3）在DMSCN中利用加权稀疏表示，保证数据的局部性，从而实现更高效和准确的数据表示。（4）模型中低维共识子空间能聚合来自所有子空间的聚类信息。图3 中We,Wd分别表示编码层和解码层的权重矩阵。

在DMSCN 中为了执行每一个视图的N个非线性变换，对每一个视图采用N+1 层的神经网络，其中每个第一层表示数据的输入。第一个N2 隐藏层作为编码器的输出用于学习紧凑表示，最后一个N2 层作为编码器的输入保证数据的全局性。此外说明一下符号表示，如表示数据集中第v个视图中输入的一个数据点，以及式（10）中表示第v个视图的第n层的输出。

图3 DMSCN结构体系

其中，索引层数表示为n=1,2,…,N。dnv表示第v个视图相应层的神经元数，σ(· )表示使用的激活函数。

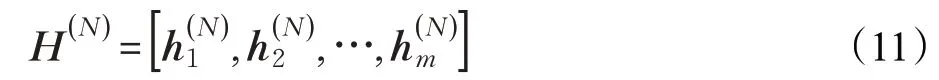
为了保证数据全局结构，如2.2 节所述在网络的编码层和解码层之间引入自表示层，通过学习低秩子空间表示来进一步增强聚类结构：

J1中Cv和分别表示第v个视图的子空间表示和自表示层，N一般为偶数。非负约束Cv≥0 是为了约束其解。通过自表示学习，Cv中的每个元素都反映两个样本之间的相似性。为了确保Cv的块对角线属性，采用核范数进行约束，这样可以有效地增强数据相关性并揭示不同视图中固有的低秩聚类结构。

在大多数子空间聚类中，数据的局部结构很容易被忽略。近年来许多研究[20-21]表明数据局部结构的重要性，虽然一部分方法使用L1 范数的稀疏约束自适应地选取少量样本进行数据表示，但由于稀疏性并不一定保证了局部性，也不能捕捉到数据固有的局部性结构。为了保证数据局部性，在模型中引入一个距离约束。另外考虑到视图之间互补性和多样性，建议学习低维共识子空间F∈ℝn×s，它可以在不同视图中交替学习视图的特征：J2中[χ1,χ2,…,χn]∈ ℝm×n表示每个视图中包含n个样本的数据矩阵，其中每个样本表示为一个列向量。正交约束FTF=I避免平凡解，tr(· )表示矩阵的迹操作。

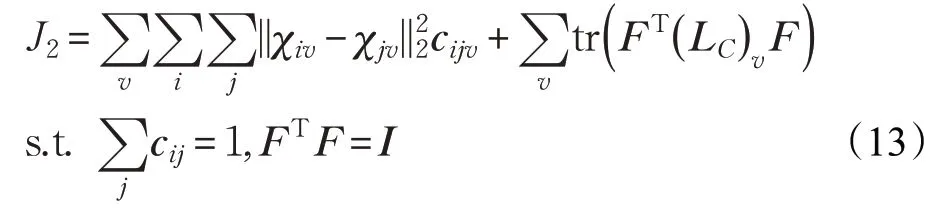
通过组合上述问题形成整体目标函数。对于多视图子空间聚类建议最小化以下目标函数：

其中，参数λ1,λ2为权衡参数。求解式（14）可以通过不同视图的低秩子空间来学习共识子空间F，然后将共识子空间作为新的数据表示，然后对其进行聚类分析，得到多视图子空间聚类结果。

4 优化

在本章中，使用随机子梯度下降法算法来优化深度自编码的多视图子空间聚类网络。在每次迭代中，固定其他变量只更新一个变量。重写式（14）为下面形式：

首先根据式（10）中对的定义，使用反向传播算法更新W(n)和b(n)。

（1）更新Wn和bn

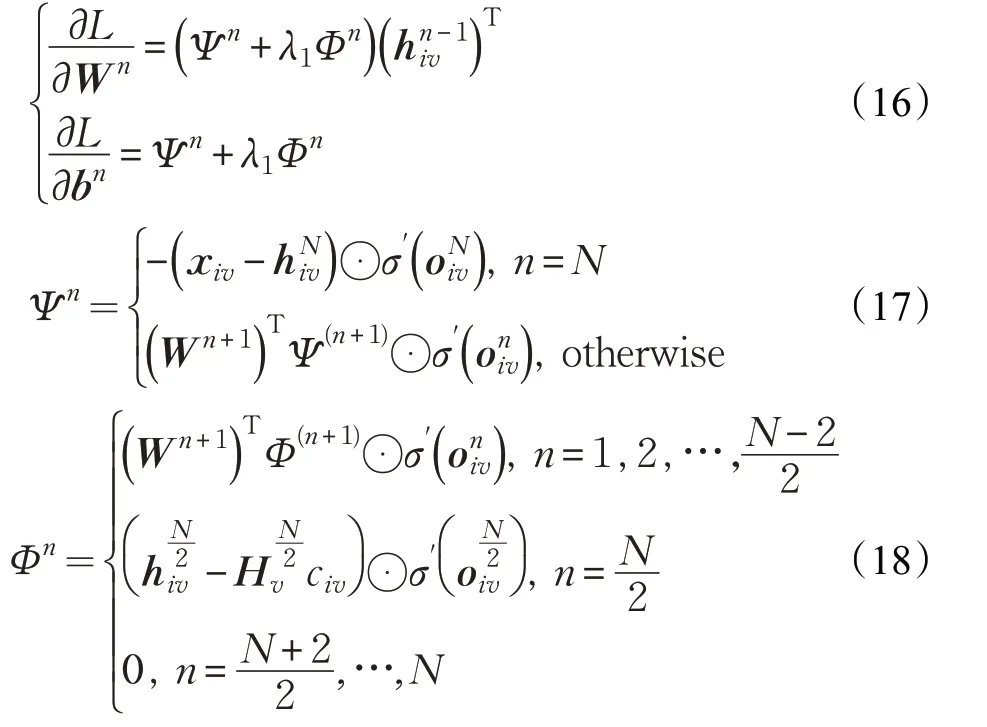
其中，⊙ 叫作 Hadamard 积，σ′(· )表示σ(· )的导数，使用随机子梯度下降法算法，Wn和bn更新（其中学习率ε=10-3）如下：

然后从式（15）保留其余变量，以及为了使其可分离进行优化引入辅助变量P，得到以下问题：

（2）更新civ

式（21）的增广拉格朗日函数是：

式（22）采用交替最小化方法解决所有变量，设置偏导数∂L(civ,Y1,Y2)∂(civ)=0 解决civ并获得：

其中，G=Y1+D1,U=Y2+D2以及I是单位矩阵。为了解决Y1，设 ∂L(civ,Y1,Y2)∂(Y1)=0 并获得：

使用Θτ(X)=UΔτVT，即奇异值阈值算子解决式（25），更新Y2：

（3）更新P

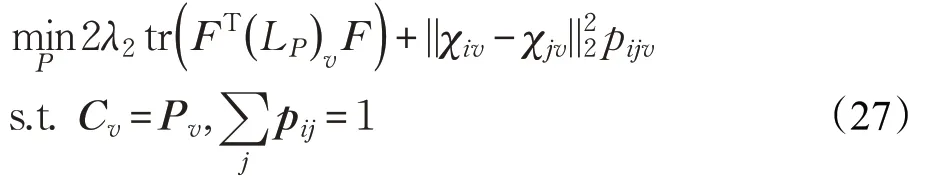
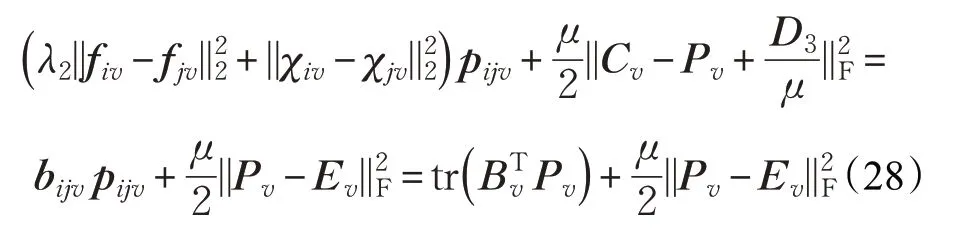
（4）更新F

其中，(LC)v是C第v个视图的拉普拉斯矩阵。式（30）可以通过特征值分解进行求解，其解是LC的最小s个特征值对应的特征向量集。

算法1深度多视图子空间聚类网络

算法1总结了模型的优化过程。在本文的实现中，使用σ(·)=tanh(· )作为激活函数并采用预训练的方式进行算法优化。先通过预训练较浅的自编码器网络，然后使用预训练的权重来初始化更深的网络。必须要指出的是，本文工作侧重于子空间聚类。

算法2更新辅助变量和拉格朗日乘子

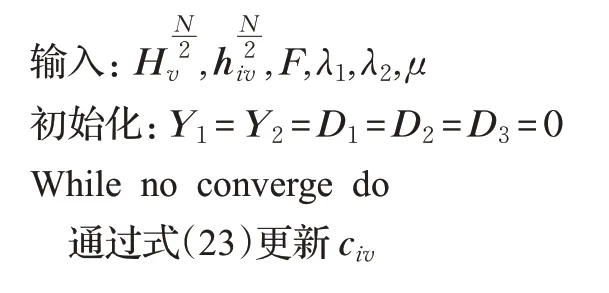
5 实验

首先，描述了实验设置，包括评估指标和比较方法。第二，实验分析，包括数据集介绍，以及参数设置和网络层结构对深度自编码多视图子空间聚类网络（DMSCN）的影响。

5.1 实验设置

在实验中为了公平，所有方法的参数都选取能使聚类结果达到最好的值，并且对每个数据集都进行10 次实验，结果取其平均值。使用两个指标来衡量聚类效果，一种为准确率（ACC）来评判所有方法的聚类性能，正确率：ACC=Naccuracy／Ntotal。其中Naccuracy表示正确样本数量，Ntotal表示样本总数。另一种为标准化互信息（NMI），其定义如下：

其中，表示样本中的第l类。np表示集群Cp的样本数目，np,l表示第l类和集群Cp交集的样本数目。可以看出NMI 的取值范围是从0 到1，NMI 数值越大表示两个集群的相似度越大。将本文方法与五种先进的多视图聚类方法进行比较，如 DiMSC[9]、ECMSC[10]、MVSC[11]、NaMSC、SWMC[22]。

5.2 实验分析

5.2.1 数据集

对三个广泛使用的数据集如3-Sources 数据、Cornell 数据集、Numerals 数据集，进行深度自编码的多视图子空间聚类网络的实验评估。本文的所有实验均在Matlab R2014a 编写运行，运行计算机处理器是1.80 GHz Intel CoreTMi5-3337U，内存为8 GB。

（1）3-Sources数据集（http：//mlg.ucd.ie/datasets/3sources.html）。Sources中收集三个著名的在线新闻源，如BBC（英国广播公司）、Reuters（路透社）、The Guardian（卫报）。这个数据集总共收集了948篇新闻文章。

（2）Cornell 数据集（http://www.cs.cmu.edu/afs/cs/project/theo-20/www/data/）。Cornell是网页数据集WebKB的其中一个子集。其中的每个数据点都由2个视图：内容和引用来描述。

（3）Numerals 数据集（http：//archive.ics.uci.edu/ml/datasets/Multiple+Features）。 Handwritten Numerals 是来自伊利诺斯大学的手写数字数据集，这个数据集包含2 000 个对应于数字数据点，这些数字由0 到9 组成，共10类。这三个数据集的基本数据特征总结在表1中。

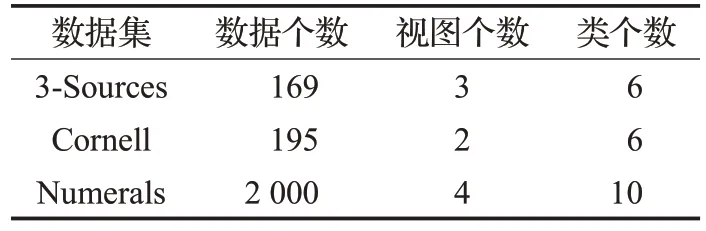
表1 多视图数据集的基本数据特征

5.2.2 参数设置

在DMSCN 中有控制参数λ1、λ2以及惩罚参数μ，为了验证参数对目标函数值准确性的影响，使用准确率作为度量，根据不同的数据集对参数λ1、λ2和μ进行调整，以观察参数值对准确率的影响。在实验中，使λ1取值围为{0.01,0.1,1,10,100} ，对于λ2不同数据集取值不同，以及其中惩罚参数μ=λ2λ1。对于不同的参数，各数据集算法准确率如图4所示。

从图4 中可以看到，算法在参数λ1、λ2、μ取不同值得到不同的聚类准确率。因此调整参数λ1、λ2、μ，能得到更好的选择结果。可见在3-Sources 数据集中λ1=1.0,λ2=10.0,μ=10.0。DMSCN的聚类误差相对较小。对于 Cornell 数据集λ1=0.1 ，λ2=0.2 ，μ=2.0 ，DMSCN 的聚类精度最高。在Numerals 数据集中λ1=0.1,λ2=30,μ=300，DMSCN的聚类效果最好。

5.2.3 层结构

为聚类网络尝试了不同的体系结构，例如，不同的网络层数和神经元数量，但当增加这些值时，虽然增加了网络的表示能力，但是它也增加了网络参数的数量。

为了研究深度自编码的多视图子空间聚类网络（DMSCN）聚类性能是如何随着层的大小和神经元的数量而变化，构建了一层到四层模型，其中一层模型即包含一层编码器和一层解码器，二层模型即包含二层编码器和二层解码器，以此类推。每个模型中又含有一个自表达层。神经元的数量在每一个模型中每层步长分别增加20，50，100，150。

不同层结构对于模型的聚类结果影响如图5所示，从图5 中可以看出，在3-Sources 数据集和Cornell 数据集中三层模型以及其神经元数量步长为100 时的NMI值最高。在一层和二层模型中，因为层数或神经元数量较少以至于无法捕捉信息的多视点数据。而在四层模型中由于包含很多的参数，导致过多的冗余信息不利于聚类。在Numerals 数据集中二层模型及神经元数量步长为50时NMI值高于其他。Numerals数据集中数据量较多，当增加模型层数和神经元数量时将会导致更多的参数，降低了聚类性能。

综上所述，在实验中对于3-Sources数据集和Cornell数据集采用三层模型以及神经元步长为100，即300-200-100-100-200-300。对于Numerals 数据集则采用二层模型及其神经元步长为50，即100-50-50-100。

5.3 实验结果以及评价

本文算法与相比较的算法均在同一实验环境下进行，最后提取10 次运行实验结果的均值评估各算法的性能，各算法在数据集上得出的实验结果如图6 所示，三个数据集在DMSCN 中的最终可视化结果如图7所示。

图4 不同参数下准确率的直方图

图5 不同层结构对聚类性能的影响

图6 各算法在不同数据集上的结果

图7 结果可视化

通过图6可以看出随着实验次数的增加，本文算法在数据集上的聚类准确率有些波动，但经过十次实验得到的平均准确率要比其他多视图子空间聚类算法高。为了更直观对比各个算法的准确率和互信息，将各算法的准确率（均值±标准偏差）以及互信息（均值±标准偏差）的统计结果列表。如表2 所示，本文算法在各个数据集上的准确率均为最高，其中比算法DiMSC 的准确率高出7.057 个百分点，比算法ECMS 的准确率高出3.048个百分点，比算法NaMSC的准确率高出12.736个百分点，比算法MVSC的准确率高出9.897个百分点，比算法SWMC的准确率高出8.938个百分点。

表2 准确率统计结果 %

从表3中可以看出，本文算法在各个数据集上互信息平均值最高，其中比算法DiMSC的互信息平均值高出1.889 个百分点，比算法ECMS 的互信息平均值高出0.826 个百分点，比算法NaMSC 的互信息平均值高出4.528 个百分点，比算法MVSC 的互信息平均值高出3.187 个百分点，比算法SWMC 的互信息平均值高出0.832个百分点。

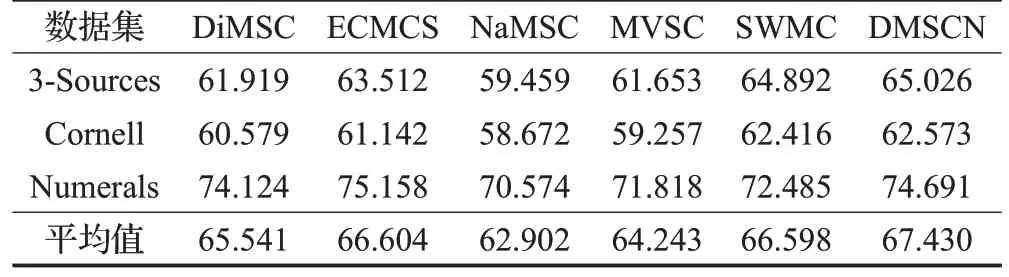
表3 互信息统计结果%

6 结束语

在本文中，基于深度自编码的多视图子空间聚类网络（DMSCN）模型主要用于多视图子空间聚类，与现有主要依赖深度学习模型的浅层多视图学习不同，DMSCN 通过利用多个层中所包含的聚类信息进一步提高了聚类性能，并利用多视图数据之间的差异性和互补性，在不同视图中交替学习聚类指示矩阵F，捕获数据的内在聚类结构，以及利用加权稀疏表示来增强子空间聚类，进而可以获得更全面和多样化的聚类信息。对几个数据集进行了实验，证明该模型的有效性。在未来的工作中将继续探索、扩展本文的深度模型和优化策略。